Farin G. Curves and Surfaces for CAGD. A Practical Guide

Подождите немного. Документ загружается.

162 Chapter 9 Constructing Spline Curves

simplistic to cope with most practical situations. The reason for the overall poor^

performance of the uniform parametrization can be blamed on the fact that it

"ignores" the geometry of the data points.

The following is a heuristic explanation of this fact. We can interpret the

parameter u of the curve as time. As time passes from time

to time u^^

the point x(w) traces the curve from point x(wo) ^^ point x(wj^). With uniform

parametrization, x(w) spends the same amount of time between any two adjacent

data points, irrespective of their relative distances. A good analogy is a car driving

along the interpolating curve. We have to spend the same amount of time between

any two data points. If the distance between two data points is large, we must

move with a high speed. If the next two data points are close to each other, we

will overshoot since we cannot abruptly change our speed—we are moving with

continuous speed and acceleration, which are the physical counterparts of a C^

parametrization of a curve. It would clearly be more reasonable to adjust speed

to the distribution of the data points.

One way of achieving this is to have the knot spacing proportional to the

distances of the data points:

A. _ IIAp.ll (9^^^)

A,+i ||Ap,-+i||

A knot sequence satisfying (9.15) is called chord length parametrization. Equa-

tion (9.15) does not uniquely define a knot sequence; rather, it defines a whole

family of parametrizations that are related to each other by affine parameter

transformations. In practice, the choices

= 0 and

ui^

lor:uQ^

= 0 and ui = L

are reasonable options.

Chord length usually produces better results than uniform knot spacing,

although not in all cases. It has been proven (Epstein [186]) that chord length

parametrization (in connection with natural end conditions) cannot produce

curves with corners^ at the data points, which gives it some theoretical advantage

over the uniform choice.

Another parametrization has been named "centripetal" by E. Lee

[378].

It is

derived from the physical heuristics presented earlier. If we set

There are cases in which uniform parametrization fares better than other methods. An

interesting example is in Foley

[239],

p. 86.

A corner is a point on a curve where the tangent (not necessarily the tangent vector!)

changes in a discontinuous way. The special case of a change in 180 degrees is called a

cusp;

it may occur even using the chord length parametrization.

A,+i

9.6 Finding a Knot Sequence 163

,1/2

lApil'

|Api+ill

(9.16)

the resulting motion of a point on the curve will "smooth out" variations in the

centripetal force acting on it.

Yet another parametrization v^as developed by G. Nielson and T. Foley

[449].

It sets

A,-

= di

where dj =

Ap^||

and

^ 3 Q/4-1 3 0^+i4fl

2 di_i + dj 2 dj -h

di_^i

(9.17)

0; = min

(.-e,.|).

and 0/ is the angle formed by p/-i, P/, p^+i- Thus 0^ is the "adjusted" exterior

angle formed by the vectors Ap/ and

Ap^.j.

As the exterior angle 0^ increases,

the interval A^ increases from the minimum of its chord length value up to a

maximum of four times its chord length value. This method was created to cope

with "wild" data sets.

We note one property that distinguishes the uniform parametrization from its

competitors: it is the only one that is invariant under affine transformations of the

data points. Chord length, centripetal, and the Foley methods all involve length

measurements, and lengths are not preserved under affine maps. One solution to

this dilemma is the introduction of a modified length measure, as described in

Nielson

[446].^

For more literature on parametrizations, see Cohen and O'Dell

[122],

Hartley

and Judd

[314], [315],

McConalogue

[421],

and Foley

[239].

Figures 9.14 to

9.21^^

show the performance of the discussed parametrization

methods for one sample data set. For each method, the interpolant is shown

together with its curvature plot. For all methods, Bessel end conditions were

chosen.

Although the figures are self-explanatory, some comments are in order. Note

the very uneven spacing of the data points at the marked area of the curves. Of

all methods, Foley's copes best with that situation (although we add that many

examples exist where the simpler centripetal method wins out). The uniform

9 The Foley parametrization was in fact first formulated in terms of that modified length

measure.

10 Kindly provided by

Foley.

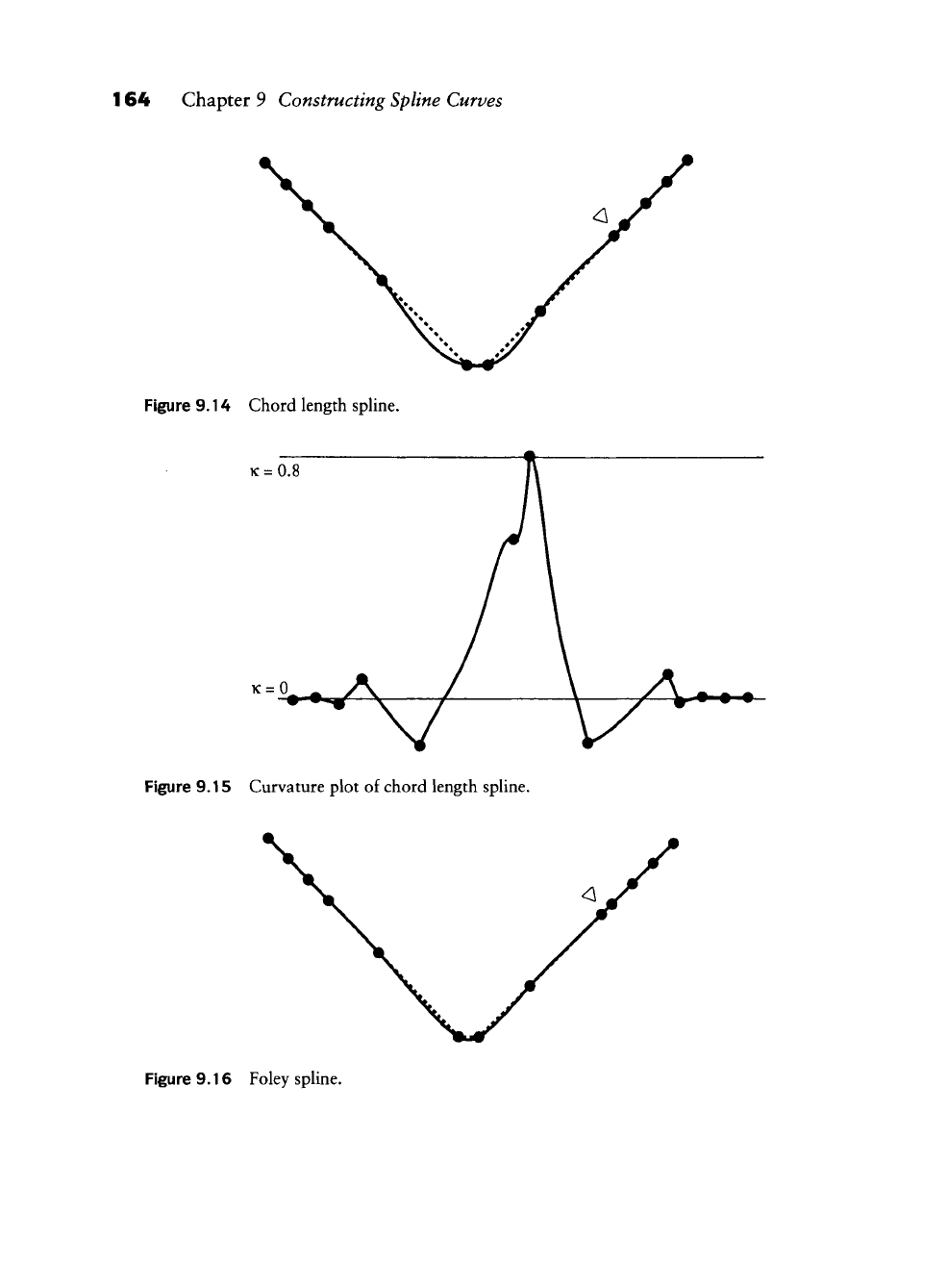
164 Chapter 9 Constructing Spline Curves

Figure 9.14 Chord length sphne.

K =

0.8

Figure 9.15 Curvature plot of chord length spUne.

Figure 9.16 Foley spline.

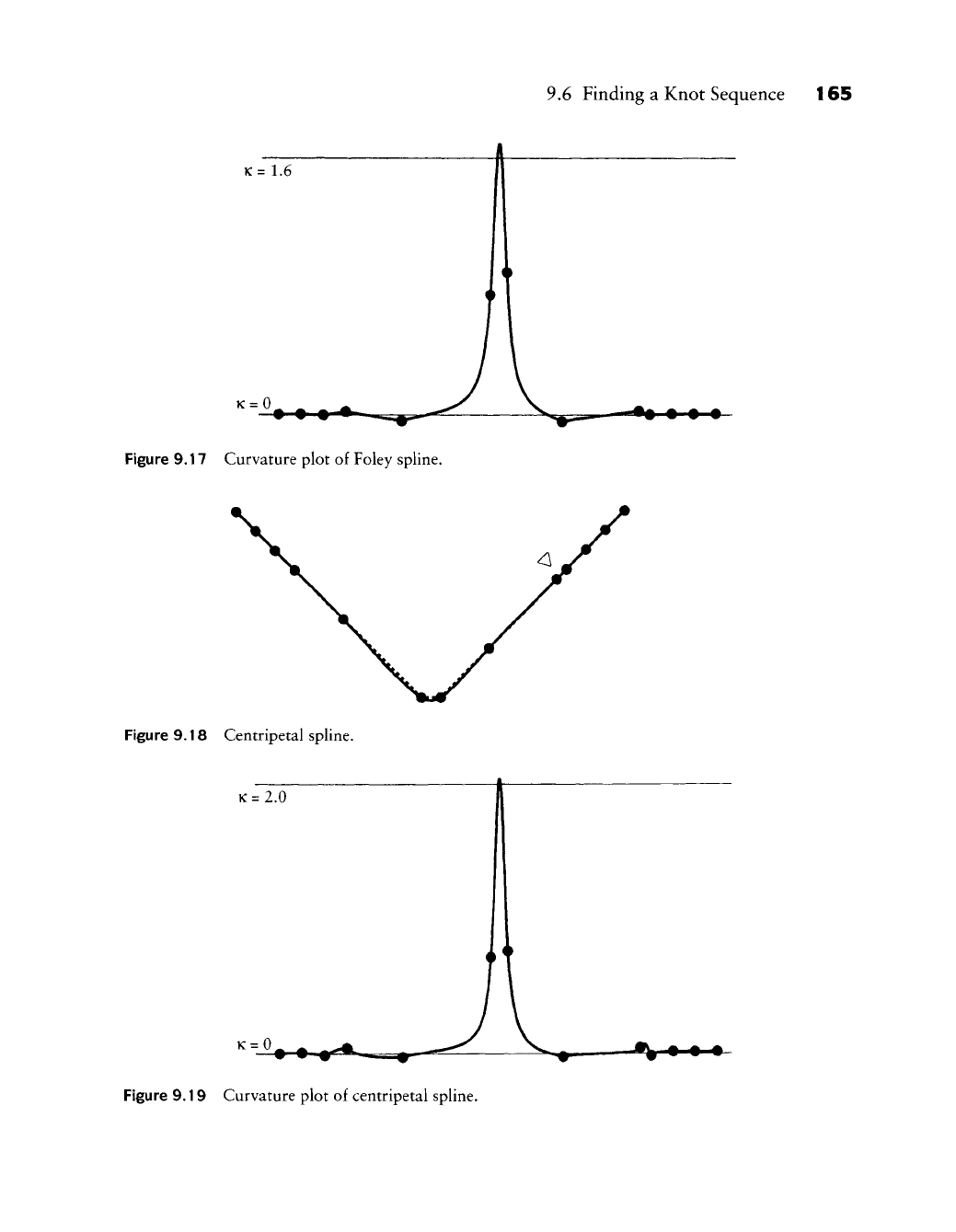
9.6 Finding a Knot Sequence 165

K= 1.6

K=0

Figure 9.17 Curvature plot of Foley spline.

Figure 9.18 Centripetal spline.

K =

2.0

K=0

Figure 9.19 Curvature plot of centripetal spline.

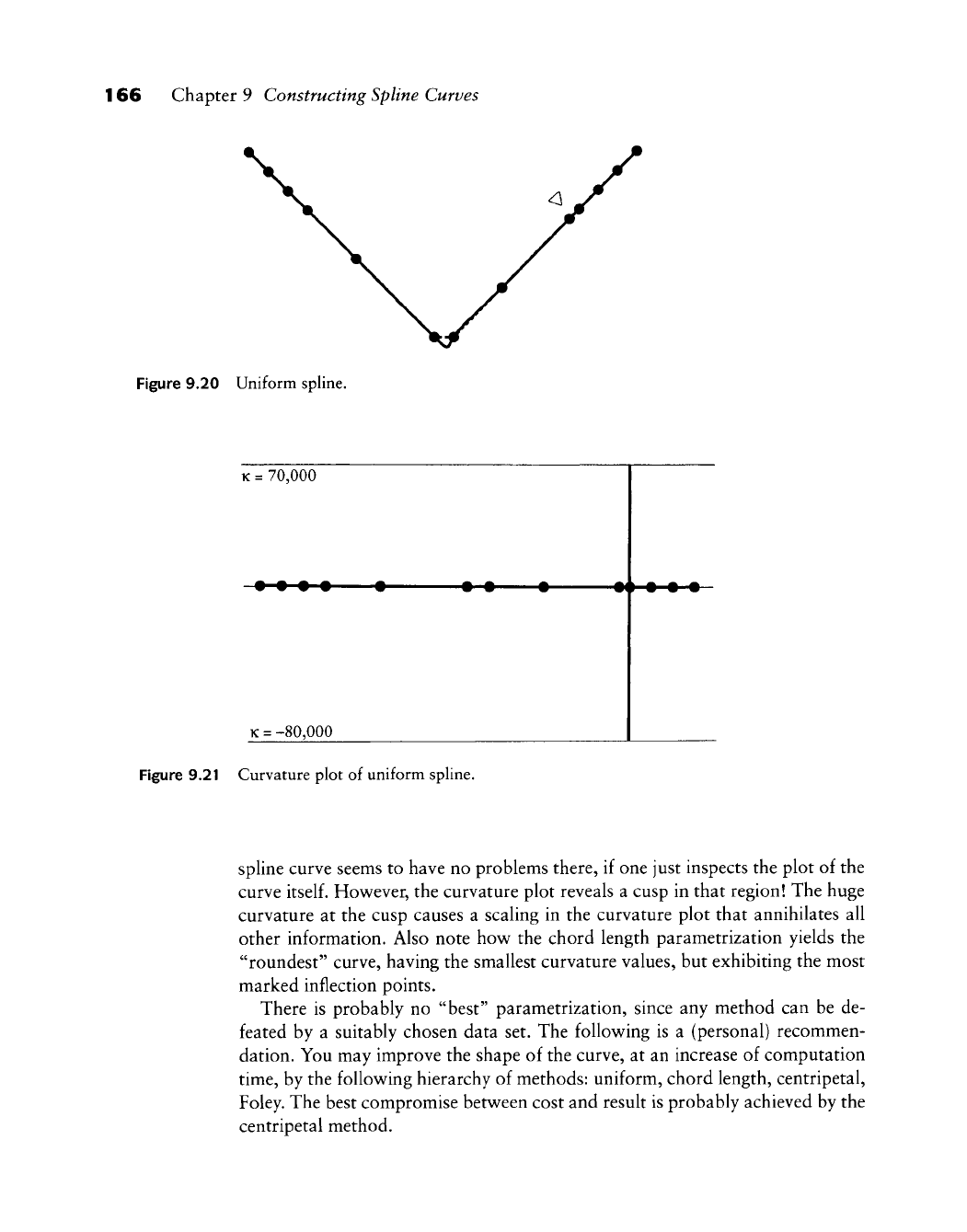
166 Chapter 9 Constructing Spline Curves

Figure 9.20 Uniform spline.

K =

70,000

• • • • •

• • • •• • • •

K =

-80,000

Figure 9.21 Curvature plot of uniform spline.

Spline curve seems to have no problems there, if one just inspects the plot of the

curve

itself.

However, the curvature plot reveals a cusp in that region! The huge

curvature at the cusp causes a scaling in the curvature plot that annihilates all

other information. Also note hov^ the chord length parametrization yields the

"roundest" curve, having the smallest curvature values, but exhibiting the most

marked inflection points.

There is probably no "best" parametrization, since any method can be de-

feated by a suitably chosen data set. The foUov^ing is a (personal) recommen-

dation. You may improve the shape of the curve, at an increase of computation

time,

by the follov^ing hierarchy of methods: uniform, chord length, centripetal,

Foley. The best compromise betv^een cost and result is probably achieved by the

centripetal method.

9.7 The Minimum Property 167

9.7 The Minimum Property

In the early days of design, say, ship design in the 1800s, the problem had to be

handled of how to draw (manually) a smooth curve through a given set of points.

One way to obtain a solution was the following: place metal weights (called

ducks) at the data points, and then pass a thin, elastic wooden beam (called a

spline) between the ducks. The resulting curve is always very smooth and usually

aesthetically pleasing. The same principle is used today when an appropriate

design program is not available or for manual verification of a computer result;

see Figure 9.22.

The plastic or wooden beam assumes a position that minimizes its strain

energy. The mathematical model of the beam is a curve s, and its strain energy

£ is given by

(s)fds,

where

denotes the curvature of the curve. The curvature of most curves involves

integrals and square roots and is cumbersome to handle; therefore, one often

approximates the preceding integral with a simpler one:

s{u)

du.

(9.18)

Note that E is a vector; it is obtained by performing the integration on each

component of s.

Equation (9.18) is more directly motivated by the following example: when

an airplane is scheduled to fly from A to B, it will have to fly over a number of

intermediate "way points." The amount of fuel used by an airplane is mostly af-

fected by its acceleration, which is essentially equivalent to the second derivative

Figure 9.22 Spline interpolation: a plastic beam, the spline, is forced to pass through data points,

marked by metal weights, the ducks.

168 Chapter 9 Constructing Spline Curves

of its trajectory. Thus if the plane follows a cubic spline curve passing through

all the way points, it will be guaranteed to use the least amount offuell^i

In a more general setting, we may word this as: among all C^ curves inter-

polating the given data points at the given parameter values and satisfying the

same end conditions, the cubic spline yields the smallest value for each compo-

nent of E. For a

proof,

let s{u) be the C^ cubic spline and let y{u) be another C^

interpolating curve. We can write y as

y{u) = s(u) + [y(u) - s(u)l

The preceding integrals are defined componentwise; we will show the minimum

property for one component only. Let s(u) and y(u) be the first component of s

and y, respectively. The "energy integral" E of y's first component becomes

pUi pUi pUi

E= (sfdu + 2 / s(y - s)du + / (y - sfdu.

JUQ JUQ JUQ

We may integrate the middle term by parts

I s(y

—

s)du = s(y

—

s) — / s\y

—

s)du,

Jua '"0 Juo

The first term vanishes because of the common end conditions. In the second

term, s is piecewise constant:

UT ^-1

"s{y

- s)du = ^ Sj(y - s)

"0 /=o

All terms in the sum vanish because both s and y interpolate. Since

/ {y - 'iydu > 0

JUQ

for continuous y ^ s,

f ^(yfdu

f ^(sfdu, (9.19)

JUQ JUQ

we have proved the claimed minimum property.

11 I am grateful to

Crouch for bringing the airplane analogy to my attention.

9.8 C^ Piecewise Cubic Interpolation 169

The minimum property of splines has spurred substantial research activity.

The replacement of the actual strain energy measure £ by E is motivated by the

desire for mathematical simplicity. The curvature of a curve is given by

, , IIXAXII

llxlP

But we need ||x|| ^ 1 in order for ||x|| to be a good approximation to /c. This

means, how^ever, that the curve must be parametrized according to arc length;

see (10.7). This assumption is not very realistic for cubic splines in a design

environment; see Problems.

While the classical spline curve merely minimizes an approximation to (9.18),

methods have been developed that produce interpolants that minimize the true

energy (9.18), see

[425],

[99]. Moreton and Sequin have suggested to minimize

the functional f[K\t)f-dt instead; see

[431].

9.8 C^ Piecewise Cubic Interpolation

Spline curves come in the B-spline form, but they may also be described as

piecew^ise Bezier curves. We now^ consider that approach, applied to piecewise

cubic interpolation. First, v^e try to solve the foUow^ing problem:

Given: Data points

XQ,

...,

x^^

and tangent directions

IQ,

...,

at those data

points; see Figure 9.23.

Find:

A C^ piecewise cubic polynomial that passes through the given data

points and is tangent to the given tangent directions there.

It is important to note that we only have tangent directions^ that is, we have

no vectors with a prescribed length since our problem statement did not involve

Figure 9.23 C^ piecewise cubics: example data set.

170 Chapter 9 Constructing Spline Curves

a knot sequence. We can assume without loss of generahty that the tangent

directions

have been normahzed to be of unit length;

111;

The easiest step in finding the desired piecewise cubic is the same as before: the

junction Bezier points

hi^i

are again given by b3/ = X/, / = 0,..., L.

For each inner Bezier point, we have a one-parameter family of solutions: we

only have to ensure that each triple h^i-i-,

h^^i^

^^i^^i

is coUinear on the tangent at

hi^i

and ordered by increasing subscript in the direction of

1^.

We can then find a

parametrization with respect to which the generated curve is C^ [see (5.30)].

In general, we must determine the inner Bezier points from

b3/+i = b3,+a,l„ (9.20)

b3.-i = b3,-^,_il„ (9.21)

so that the problem boils down to finding reasonable values for oti and )6^.

Although any nonnegative value for these numbers is a formally valid solution,

values for a^ and Pi that are too small cause the curve to have a corner at x^,

whereas values that are too large can create loops. There is probably no optimal

choice for of/ and Pi that holds up in every conceivable application—an optimal

choice must depend on the desired application.

A "quick and easy" solution that has performed decently many times (but also

failed sometimes) is simply to set

a, = ft = 0.4||Ax,||. (9.22)

(The factor 0.4 is, of course, heuristic.)

The parametrization with respect to which this interpolant is C^ is the chord

length parametrization. It is characterized by

A, _ ft _ ||Ax,|| ^^^^^^

A,+i a,+i ||Ax,+i||

A more sophisticated solution is the following: if we consider the planar curve

in Figure 9.24, we see that it can be interpreted as a function, where the parameter

t varies along the straight line through

b3^

and

b3^_^3.

Then

l|Ab3,||-'l''^'>^-^^'l'

3 cos 0/

COS

^ij^i

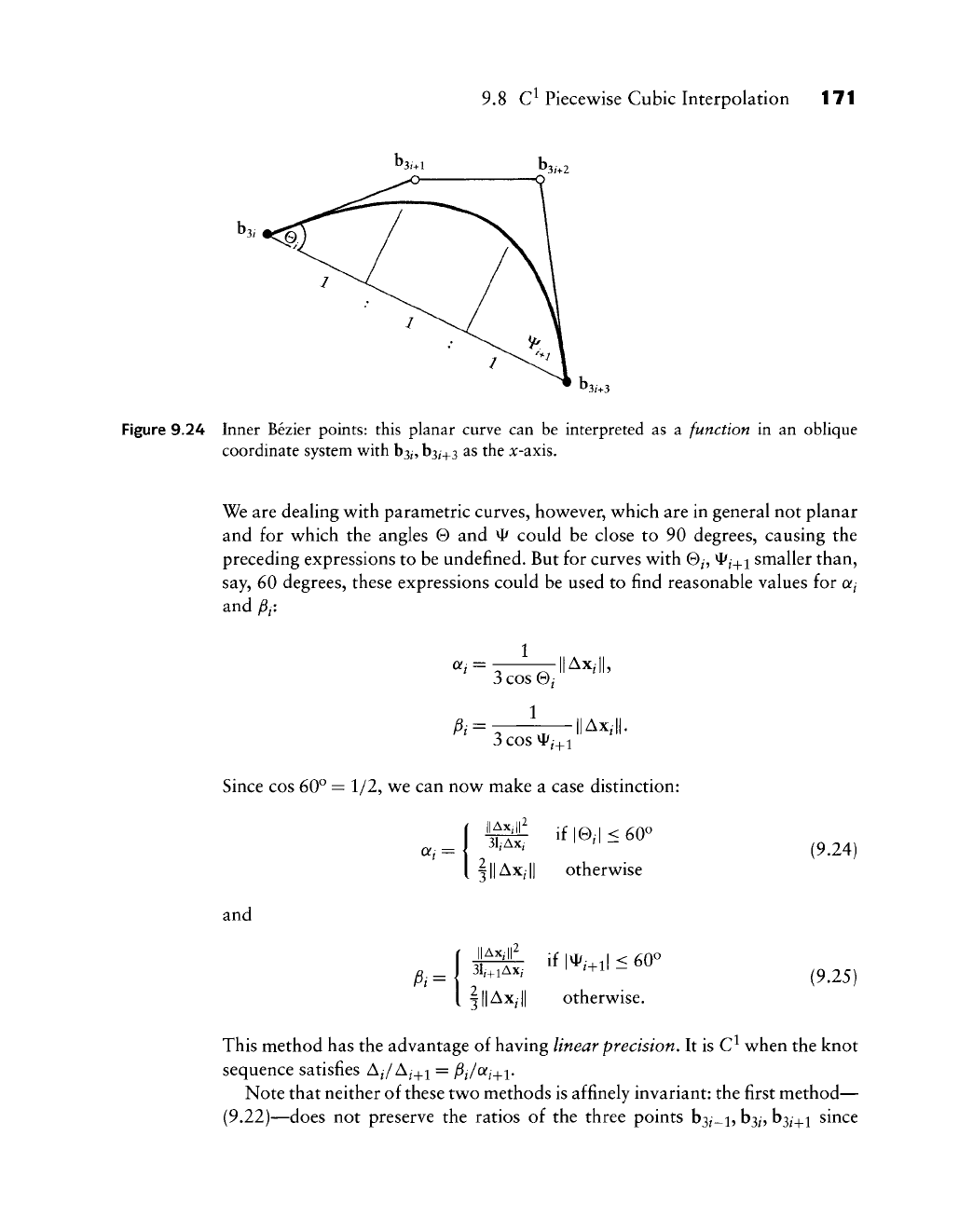
9.8 C^ Piecewise Cubic Interpolation 171

Figure 9.24 Inner Bezier points: this planar curve can be interpreted as a function in an oblique

coordinate system with

b3/,

b3/+3

as the x-axis.

We are dealing with parametric curves, however, which are in general not planar

and for which the angles 0 and ^ could be close to 90 degrees, causing the

preceding expressions to be undefined. But for curves with 0^, ^^_^i smaller than,

say, 60 degrees, these expressions could be used to find reasonable values for of/

and ^i'.

3 cos 0/

lAX;

Ax,

3 cos ^ij^\

Since cos 60^ = 1/2, we can now make a case distinction:

iiAx,r

31/Ax,

if |0,| < 60^

|||Ax;|| Otherwise

(9.24)

and

Ax,

^,=

131;;^

if|*ml<60°

lAX;

Otherwise.

(9.25)

This method has the advantage of having linear precision. It is C^ when the knot

sequence satisfies Aj/Aj^i = ^i/oti^\.

Note that neither of these two methods is affinely invariant: the first method—

(9.22)—does not preserve the ratios of the three points b3,_i, b3p b3/_^i since