Фафурин В.А., Терюшов И.Н. Автоматизация технологических процессов и производств
Подождите немного. Документ загружается.

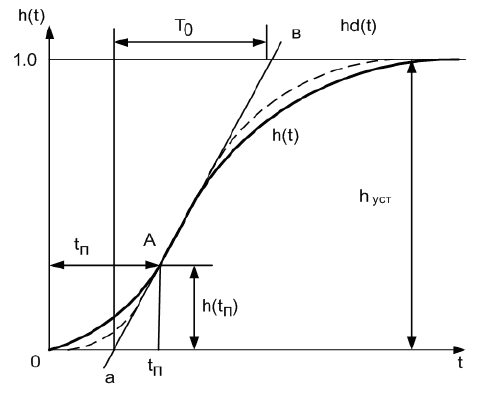
Рис.8.21. Определение динамических параметров объекта
согласно методичке [3]
3. Исходя из найденных таким образом b и n, по таблицам
определяют отношения Т
1
/ Т
2
, Т
2
/ Т
1
, t
ПА
/Т
1
, что позволяет определить
последовательно постоянные временим Т
1
и Т
2
, а также величины
t
ПА
*
.
___________________________________________________________
*
При использовании таблиц численные значение параметров внутри
интервалов можно определить, используют метод линейной интерполяции.
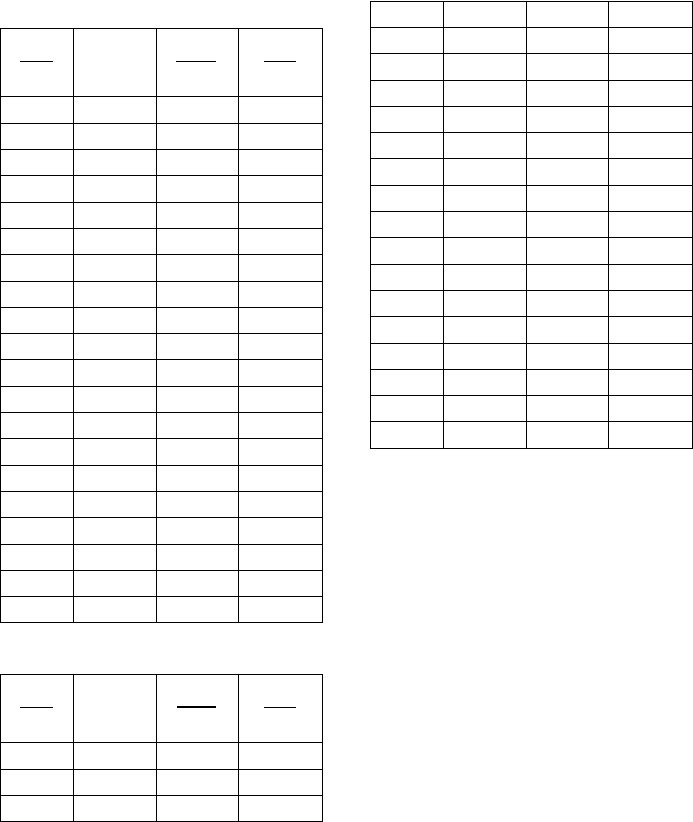
Таблицы для определения параметров математической
модели (n–показатель, определяющий порядок
аппроксимирующий передаточной функции)
Таблица 8.3 (n=1)
2
1
Т
Т
b
1
ПА
Т
t
0
1
Т
Т
0.05 0.103 0.158 0.804
0.10 0.148 0.256 0.774
0.15 0.177 0.335 0.715
0.20 0.197 0.402 0.669
0.25 0.212 0.462 0.630
0.30 0.224 0.516 0.597
0.35 0.223 0.565 0.568
0.40 0.240 0.661 0.543
0.45 0.245 0.653 0.520
0.50 0.250 0.693 0.500
0.55 0.254 0.731 0.482
0.60 0.256 0.766 0.465
0.65 0.259 0.800 0.449
0.70 0.260 0.832 0.435
0.75 0.262 0.863 0.422
0.80 0.263 0.893 0.410
0.85 0.263 0.921 0.398
0.90 0.264 0.984 0.387
0.95 0.264 0.975 0.377
1.00 0.264 0.999 0.368
Таблица 8.4 (n=2)
2
1
Т
Т
b
1
ПА
Т
t
0
1
Т
Т
0.05 0.103 0.238 0.821
0.10 0.186 0.402 0.723
0.15 0.222 0.541 0.653
0.20 0.257 0.665 0.598
0.25 0.256 0.779 0.553
0.30 0.278 0.885 0.515
0.35 0.289 0.985 0.482
0.40 0.297 1.079 0.454
0.45 0.303 1.170 0.429
0.50 0.308 1.256 0.407
0.55 0.312 1.340 0.387
0.60 0.315 1.421 0.369
0.65 0.318 1.500 0.353
0.70 0.319 1.576 0.338
0.75 0.321 1.651 0.325
0.80 0.322 1.723 0.321
0.85 0.323 1.795 0.301
0.90 0.323 1.864 0.290
0.95 0.323 1.933 0.280
1.00 0.323 2.000 0.271
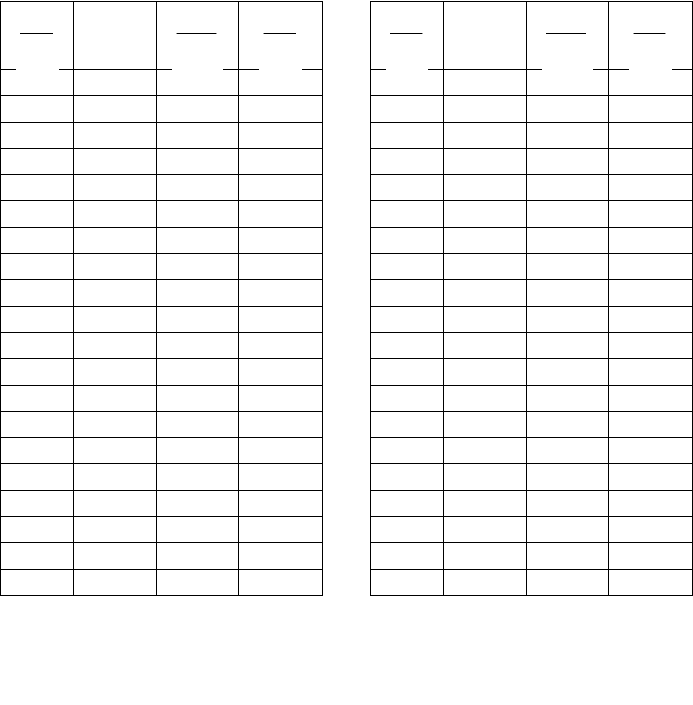
Таблица 8.5 (n=3)
2
1
Т
Т
b
1
ПА
Т
t
0
1
Т
Т
0.05 0.147 0.308 0.798
0.10 0.210 0.533 0.690
0.15 0.249 0.782 0.613
0.20 0.276 0.906 0.554
0.25 0.295 1.072 0.506
0.30 0.309 1.228 0.446
0.35 0.319 1.376 0.433
0.40 0.327 1.520 0.404
0.45 0.333 1.658 0.378
0.50 0.338 1.793 0.356
0.55 0.342 1.924 0.336
0.60 0.345 2.052 0.319
0.65 0.348 2.178 0.303
0.70 0.349 2.300 0.288
0.75 0.350 2.410 0.275
0.80 0.351 2.540 0.263
0.85 0.352 2.656 0.252
0.90 0.353 2.773 0.242
0.95 0.352 2.886 0.233
1.00 0.353 2.999 0.224
Таблица 8.6 (n=4)
2
1
Т
Т
b
1
ПА
Т
t
0
1
Т
Т
0.05 0.161 0.375 0.780
0.10 0.228 0.656 0.664
0.15 0.296 0.903 0.583
0.20 0.269 1.136 0.521
0.25 0.315 1.352 0.472
0.30 0.330 1.559 0.423
0.35 0.340 1.785 0.398
0.40 0.348 1.950 0.398
0.45 0.354 2.136 0.344
0.50 0.358 2.318 0.322
0.55 0.362 2.498 0.303
0.60 0.364 2.673 0.285
0.65 0.367 2.846 0.270
0.70 0.368 3.019 0.256
0.75 0.369 3.184 0.244
0.80 0.370 3.350 0.232
0.85 0.370 3.514 0.222
0.90 0.371 3.678 0.212
0.95 0.371 3.840 0.203
1.00 0.371 4.000 0.195
Если найдено при этом значении t
ПА
окажется меньше t
П
,
найденного из аппроксимируемой характеристики h(t), то в модель
необходимо ввести время запаздывания
ПАП
ttτ
.
Оценка точности аппроксимации
Оценку точности аппроксимации будет осуществлять по
программе «ЦАСР РПФ». Расчет переходной функции модели, в
которой аппроксимирующая функция представлена в виде

321
n
2
n
1
n
τр
а
1Tpα1рТα1pT
Ке
pW
, (140)
где k, τ – коэффициенты передачи и запаздывания объекта по каналу
регулирования; Т - постоянная времени объекта; α
1
, α
2
–
коэффициенты (0<
1
α
,
2
α
<1,); n
1
, n
2
, n
3
– показатели степеней
сомножителей знаменателя выражения (140).
Используем описанную методику для определения параметров
модели по переходной характеристике, приведенной на рис.8.20.
1. Определяем исходные данные для аппроксимации -
величины h
уст
, h(t
П
), t
П
T
0
.
Имеем (см. рис.8.21) h
уст
=1; h(t
П
)=0.340; t
П
=4,70 мин; T
0
= 5,40.
2. Находим величину b=h(t
П
)/h
уст
и по таблицам для определения
параметров математической модели определяем порядок n
аппроксимирующей передаточной функции (137).
Имеем
b= h(t
П
)/ h
уст
=0.340/1=0.340, при b=0.340, n
3.4
Принимаем n=3.
3. По таблице 8.5 определяем отношения Т
1
/Т
0
, Т
2
/Т
1
, t
ПА
/Т
1
и,
следовательно, величины Т
1
, Т
2
, t
ПА
.
Имеем
Т
1
/Т
0
=0,346; Т
2
/Т
1
=0,525; t
ПА
/ Т
1
=1,8585;
Т
1
=0,346 · Т
0
=0,346 · 5,40=1,87 мин;
Т
2
=0,525 · Т
1
=0,525 · 1,87=0,98 мин;
t
ПА
=1,8585 · Т
1
=1,8585 · 1,87=3,47 мин.
Поскольку t
П
> t
ПА
находим время запаздывания
ПАП
ttτ
:
τ = 4,70 – 3,48 = 1,22 мин.
Найдём численное значение коэффициента передачи k,
входящего выражение для аппроксимирующей передаточной функции
(137).
Имеем
P
x
θ
k
= 17
о
С / 10% хода р.о.= 1,7
о
С / % хода р.о
где Δθ(∞) - отклонение температуры в переходном режиме при t
(см. рис. 8.19); Δх
Р
– принятая в расчете величина возмущения по
каналу регулирующего органа, равна 10% .
С учетом найденных значений k, τ, Т
1
, Т
2,
n аппроксимирующая
передаточная функция запишется в виде
3
р22,1
а
1р98,01p87,1
е76,1
pW
.
(141)
Оценка точности аппроксимации
При сценке точности аппроксимации в передаточной функции
(140), согласно (137), (141), необходимо положить:
.0n;3n;0α,525;0α
;1n,87;1T1,22;τ;7,1К
3221
1
Расчет на ЭВМ переходной функции модели (141) и сравнение
ее с заданной, приведенной на рис.21 показывает, что модель (119)
адекватна реальному процессу. Максимальное отклонение друг от
друга ординат аппроксимирующей переходных характеристик не
превышает 1% (при допустимых 5%).
7. Использование математических моделей динамики для
решения задач автоматизации объектов
Зная динамические характеристики объекта по основным
каналам передачи воздействий (каналам управления и каналам
возмущающих воздействий), можно решить задачу построения
эффективных АСР технологических параметров процесса,
обеспечивающих качественную стабилизацию материальных и
энергетических потоков в соответствии с требованиями
технологического регламента. Причем, динамические характеристики
объекта по каналу регулирования используются для выбора закона
регулирования регулятора и расчета его настроечных параметров, а по
каналу возмущения - для расчета переходных процессов в АСР и
оценки качества их работы (по динамической точности,
быстродействию и др. показателям).
Для решения задач автоматического регулирования, синтеза
оптимальных АСР параметров процесса могут быть использованы как
чисто инженерные методы расчета [1], так и частотные методы,
основанные на использовании нормальных и расширенных частотных
характеристик [3.5].
В данной лабораторной работе для решения задач синтеза АСР
будем использовать методику и программное обеспечение,
разработанное и подробно описанное в работе [3].
8. Исходные данные и порядок выполнения лабораторной
работы
1. Объекты автоматизации: объекты регулирования давления и
уровня (рис. 8.1, 8.3), смеситель (рис. 8.4), испаритель (рис. 8.5),
колонна ректификации (рис. 8.6), объекты автоматизации,
рассмотренные в работe[3]: теплообменник (рис. 2.9), смесительная
камера сушильной установки (рис.2.10), сушильной установка
кипящим слоем(рис.2.11), насадочный абсорбер(рис.2.12), колонна
ректификации(рис. 2.13).
2. Уравнение динамики перечисленных выше объектов (14,15);
(27,28); (45,46); (56,63,64); (75,78,79,80); таблицы динамических
параметров (2.2–2.16) для объектов, приведенных в методическом
пособии [3].
3. Конструктивные, режимные и технологические параметры,
необходимые для расчета динамических параметров объектов по
формулам (14,15); (27,28); (45,46); (56,63,64); (75,78,79,80), а также
требования к качеству работы проектируемых АСР задаются
преподавателем перед началом работы.
Требуется
1. Из приведенных в теоретическом разделе работы уравнений
динамики получить выражение для передаточных функций объекта по
соответствующим каналам передачи воздействий.
2. Используя частотные методы исследования устойчивости и
качества работ АСР и программное обеспечение по расчету АСР,
приведенное в методическом пособии [3], решить задачу
автоматического регулирования режимов работы, приведенных выше
объектов*, и оценить качественные показатели функционирования
рассчитанных АСР (динамическую ошибку, время регулирования и
степень затухания переходных процессов).
Порядок выполнения лабораторной работы
1. Получить у преподавателя задание на объект или группу
объектов, математические модели которые необходимо построить.
2. Используя задаваемые преподавателем конструктивные,
режимные и физические параметры объекта, получить конкретный
вид его математических моделей (в виде передаточных функций по
каналу регулирования и каналу возмущающих воздействий).
3. Выбрать одну, две определяющих режим работы объекта АСР
и произвести их расчет на устойчивость и качество работы, используя
для этого метод и программы расчета, приведенные в методическом
пособии [3].
4. Путем проведения машинного эксперимента оценить качество
рассчитанных АСР по динамической точности, быстродействию и
степени затухания переходных процессов.
5. Сделать соответствующие выводы по результатам работы.
____________________________________________________________
*Перечень объектов для каждого исполнителя определяет
преподаватель перед началом работы.
9. Содержание отчета
1. Краткое описание цели и основных теоретических положений
работы.
2. Математические модели (аналитические, экспериментальные)
объекта и результаты расчета АСР на устойчивость и качество работы.
3. Выводы по работе.
10. Контрольные вопросы
1. Классификация объектов с точки зрения задач
автоматизации. Объекты с сосредоточенными и распределенными
параметрами; обладающие свойством собственного
самовыравнивания и не имеющие таких свойств.
2. Сущность аналитического метода описания динамики
объектов. Уравнения единичных процессов и их физическое
истолкование.
3. Экспериментальные методы определения динамических
характеристик объектов. Сущность методов. Виды испытательных
воздействий. Переходные характеристики, импульсные функции,
частотные характеристики. Физический смысл и математическая
запись характеристик.
4. Получение по экспериментальным переходных
характеристикам передаточных функций и частотных характеристик.
5. Расчет и исследование АСР (простых и сложных) на
устойчивость и качество работы. Планирование машинного
эксперимента по проведению многовариантных расчетов АСР.
Выборы оптимального варианта системы.
Литература
1. Автоматическое управление в химической промышленности:
ученик для вузов/Е.Г. Дудунков и др.; под редакцией Е.Г. Дудункова.-
М.:Химия, 1987.-368с.
2. Бородин И.Ф. Автоматизация технологических процессов /
И.Ф.Бордин, Ю.А. Судцик.-М.:Колос, 2004.-344с.
3. Системы автоматизации и управления : лабораторный
практикум/В.А. Фафурин, И.Н. Терешов, А.И. Мухамедзянов .-
Казань:Изд–во Казанского государственного технологического
университета, 2007.-188с.
4. Полоцкий Л.М. Автоматизация химических производств.
Теория, расчет и проектирование систем автоматизации/Л.М.
Полоцкий, Г.И. Лапшенков.-М.:Химия, 1982.-296 с.
5. Ротач В.Я. Теория автоматического управления
теплоэнергетическими процессами: учебник для вузов / Ротач В.Я.-
М.:Энергоатомиздание, 1985.-296с.
