Фафурин В.А., Терюшов И.Н. Автоматизация технологических процессов и производств

 

Р,GVV

ХПКК



.

(89)

Линеаризуя зависимость (88, 89), после ряда преобразований

получим













































P

dt

Pd

P

V

P

V

RT

VM

0

П

0

K



П

0

П

0

K

0

П

G

P

V

P

V

G

V





























































ХП

0

П

0

K

0

ХП

K

G

P

V

P

V

G

V





























































(90)

или

ХП2П1

GkGkP

dt

dP

T





;

(91)

где













































0

П

0

K

P

V

P

V

VM

T

- постоянная времени;



























































0

П

0

K

0

П

1

P

V

P

V

P

V

K

- коэффициент передачи системы по

каналу

PGхх





.

При неизменном паровом потоке V

П

уравнение (II) упрощается

и принимает вид:

ХП2

GkP

dt

Pd

T







,

(92)

где

0

K

P

V

RT

VM

T

















;

(93)

.

P

V

G

V

K

0

K

0

ХП

К

2































(94)

Найдем значения производных, входящих в выражения (93, 94).

Запишем уравнение теплового баланса

 

Н

ХП

К

ХПХПжПK

qqGqqV 

.

(95)

Отсюда

 

жП

Н

ХП

К

ХПХП

K

qq

qqG

V





(96)

и

жП

Н

ХП

К

ХП

K

qq

dG

dV





,

(97)

где V

К

- количество конденсирующих паров верхнего продукта в

конденсаторе; q

П

, q

ж

– теплосодержание паровой и жидкой фаз

верхнего продукта;

Н

ХП

q

,

К

ХП

q

– теплосодержание хладоагента на

входе и выходе их конденсатора.

Значение производной

0

K

P

V















находим, используя уравнение

(96) и соотношение, связывающие давление и теплоту конденсации

насыщенных паров вещества [4].

На основе уравнения (92) находим выражение для передаточной

функции канала

РG

ХП





:

 

1Tp

K

pG

pP

pW

2

ХП







;

(98)

где

0

K

ХП

K

2

P

V

G

V

K

















.

(99)

С учетом запаздывания в импульсных линиях, измерительной и

регулирующей аппаратуре, которое можно принять равным (0,1–

0,2)Т, окончательно получим

 

pτ

2

e

1Tp

K

pW







(100)

Расчет постоянной времени Т и коэффициентов передачи К

2

.

Подставляя исходные данные в выражения (93-97), получим

 

2180

69

151

,

qq

ttG

dG

dV

жП

Н

ХП

К

ХПХП

ХП

K











(101)

ч

м

,

dР

dV

K

2

130

;

c

,

,,

T 46

831413033

360081915880









;

22

2

60681

130

2180

см

с

,

м

ч

,

K 

.

Транспортное запаздывание принимаем равным

с,Т,τ 2920 

Итак, выражение для передаточной функции канала

РG

ХП





,будет иметь вид:

 

р,

e

p,

,

pW

29

1046

60







.

(102)

На основе передаточной функции (102), а также заданных

требований к качеству работы системы регулирования давления

можно выбрать необходимый закон регулирования регулятора и

определить его настроечные параметры.

4. Математическое описание объектов с распределенными

параметрами

Выше были рассмотрены математические модели объектов

со сосредоточенными параметрами. На заводах имеется большое

число объектов, которые нельзя более или менее точно описать

обыкновенными дифференциальными уравнениями с постоянными

коэффициентами вследствие зависимости выходных параметров от

пространственных координат. Такие объекты (с распределенными

параметрами) описываются дифференциальными уравнениями

высоких порядков или дифференциальными уравнениями в частных

производных.

Рассмотрим примеры.

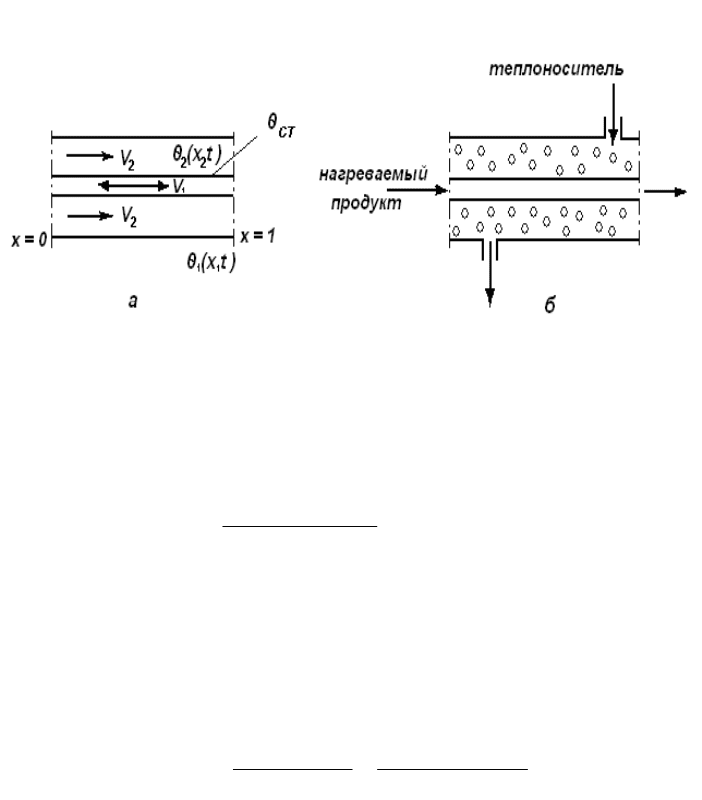
Поток жидкости в трубе. Пусть имеется труба большой длины

(рис. 8.7,а), по которой течет жидкость, нагреваемая другой

жидкостью (или газом), с более высокий температурой. Рассмотрим

элементарный объем жидкости между сечениями 1 и 2. В момент

времени t количества тепла в элементе объема Sdx равно Sρ

ж

с

ж



dx,

где S - сечение трубы; ρ

ж

- плотность жидкости; с

ж

- теплоемкость

жидкости; θ

ж

- температура жидкости; dx- расстояние между

сечениями 1 и 2.

Тепло, накопленное за промежуток времени dt в элементы Sdx,

составит:

Sdxdt

dt

)θср(

жжж



.

Поток тепла, проходящий через сечения 1 за промежуток

времени dt, будет равен ρ

ж

с

ж



V

ж

Sdt, где V

ж

– скорость движения

жидкости.

Рис. 8.7. Нагреваемый трубопровод как объект с

распределенными параметрами (а) и схема теплообменника «труба в

трубе» (б)

Вследствие транспортирования жидкости результирующее

приращение тепла в элементе dx за промежуток времени dt составит:

 

Sdxdt

Vс

жж

х

θρ

жж



Приток тепла нагреваемой жидкости от теплоносителя

вследствие теплопередачи через стенку длиной dx за время dt

определяют исходя из закона теплопередачи. Это приращение равно

QSdxdx, где Q - поток тепла в единице объема.

Используя закон сохранения энергии и выполняя

соответствующие преобразования, получим уравнение теплового

баланса:

   

0

х

θρθρ

жжж









Q

Vс

t

с

жжжж

(103)

Уравнение можно применять для анализа различных типов

жидкостных и газовых теплообменников.

Теплообмен между жидкостью в трубе и окружающей

средой. Рассмотрим динамику процесса теплообмена между

жидкостью в трубе и жидкостью, омывающий трубу (при условии

идеального перемешивания греющего агента и передачи тепла только

конвекцией). Уравнение, описывающие процесс теплообмена между

элементом жидкости в трубе и окружающий средой, будет

нелинейным, так как коэффициент теплоотдачи является функцией

температуры и скорости. В свою очередь скорость представляет собой

функцию вязкости, которая служит функций температуры. Однако

уравнение (103) можно приближенно считать линейным, если

скорость потока и температура жидкости в трубе изменяются в таких

небольших пределах, что коэффициент теплоотдачи практически от

них не зависит.

На основании уравнения (103), считая p

ж

,

с

ж

,

и V

ж

постоянными,

можно записать:

 

жCTB1

ж

жжж

ж

жж

θθdxDπαdx

х

θ

VсρSdx

t

θ

сρS 







,

(104)

где

1

α

- коэффициент теплоотдачи от стенки к жидкости; D

В

–

внутренний диаметр трубы;

СТ

θ

- температура стенки трубы.

Разделив уравнение (104) на Sρ

ж

с

ж

dx и приняв во внимание, что

Ж

ж

Sp

G

V 

, получим:

 

жСТ

жж

B1

ж

θθ

сρS

Dπα

х

θ

ρS

G

t

θ









.

(105)

Введем обозначение:

2

жж

B1

1

ж

С

сρS

Dπα

;С

Sρ

G



.

Тогда

СТ2ж2

ж

1

ж

θСθС

х

θ

С

t

θ









.

(106)

Процесс изменения во времени температуры стенки трубы

можно представить уравнением

   

жCTB1CTCH2

CT

CTB

θθDπαθθDπα

t

θ

δρDπ 



,

(107)

где

δ

- толщина стенки трубы;

С

θ

-температура греющей среды;

.СТСТ

с,ρ

- плотность и удельная теплоемкость материала трубы;

2

α

-коэффициент теплоотдачи от греющий среды к стенки; D

Н

-

наружный диаметр трубы.

Разделив уравнение (85) на коэффициент при

t

θ

СТ



, получим:

ж

CTCT

1

C

CTCTB

H2

CT

CTCT

1

CTB

H2

СТ

θ

cδρ

α

θ

cδρD

Dα

θ

cδρ

α

δρD

Dα

t

θ



















(108)

Примем, что

3

CTCTB

H2

С

cδρD

Dα



и

4

CTCT

1

С

cδρ

α



Тогда

 

θСθСθСС

t

θ

ж4C3CT43

CT





.

Таким образом, имеем два уравнения, описывающие процесс

изменения температуры жидкости

ж

θ

за счет теплопередачи от

греющий среды с температурой

С

θ

к нагреваемой жидкости в трубе,

т.е.

СТ2ж2

ж

1

ж

θСθС

х

θ

C

t

θ









;

(109)

 

ж4C3CT43

CT

θСθСθСС

t

θ





.

(110)

При выводе уравнений (109) и (110) приняты следующие

допущения:

1. Взяты усредненные значения температур по сечению

трубопровода и рассматривается лишь изменение температуры по

направлению х потока;

2. Рассматривается теплопередача только вынужденной

конвекцией;

3. Количеством тепла, проходящим в направление потока как и

жидкости, так и в стенке трубы, пренебрегаем;

4. Эффекты излучения и теплопроводности в радиальном

направлении учтены в коэффициентах теплоотдачи;

5. Теплоемкости, плотности и коэффициент теплоотдачи

конвекций приняты постоянными;

6. Механической энергией по сравнению с тепловой

пренебрегаем;

7. Потерями тепла в окружающую среду пренебрегаем.

Без учета указанных допущений уравнения получились бы очень

сложными и трудными для использования в практических расчетах.

Чтобы вывести зависимость изменения температуры

ж

θ

во

времени, необходимо решить совместно уравнения (109) и (110). Ха-

рактер переходного процесса изменения температуры на выходе из

трубы при скачкообразном изменении

С

θ

и неизменной температуре

жидкости на входе имеет вид, приведенный на рис. 6а при

скачкообразном изменении температуры на входе и неизменной

С

θ

-

на рис 8.6,б.

Теплообменник типа «труба в трубе». Рассмотрим теперь

процесс теплообмена между двумя жидкостями, протекающими в

концентрически расположенных трубах (рис.8.7,б), при котором

нагреваемой является жидкость во внутренней трубе.

Имеем три уравнения, характеризующие процесс

теплообмена:

1. для потока в трубе согласно уравнению(105)

 

1CT

111

B11

11

θθ

CρS

Dπα

x

θ

ρS

G

t

θ









;

(111)

2. для стенки согласно уравнению (107)

   

1CT

CTCT

1

CT2

CTCTB

H2

CT

θθ

cδρ

α

θθ

cδρD

Dα

t

θ





;

(112)

3. для потока в межтрубном пространстве

 

2CT

222

H22

22

θθ

CρS

Dα

x

θ

ρS

G

t

θ









. (113)

В уравнениях (111), (112) и (113) те же обозначения, что и ранее;

индексы 1 относятся к внутреннему потоку, индексы 2 — к

наружному; S

2

— сечение межтрубного пространства. Расходы G

1

и

G

2

приняты постоянными. Введя соответствующие обозначения в

уравнения (111), (112) и (113), можно переписать их в виде:

 

1CT2

1

θθС

x

θ

С

t

θ









;

(114)

   

1CT4CT23

CT

θθСθθС

t

θ





;

(115)

 

2CT6

2

5

2

θθС

x

θ

С

t

θ









. (116)

Для получения зависимости, характеризующей изменение

температуры жидкости на выходе из трубы, необходимо решить

совместно уравнения (114) - (116), дополнив их начальными и

граничными условиями.

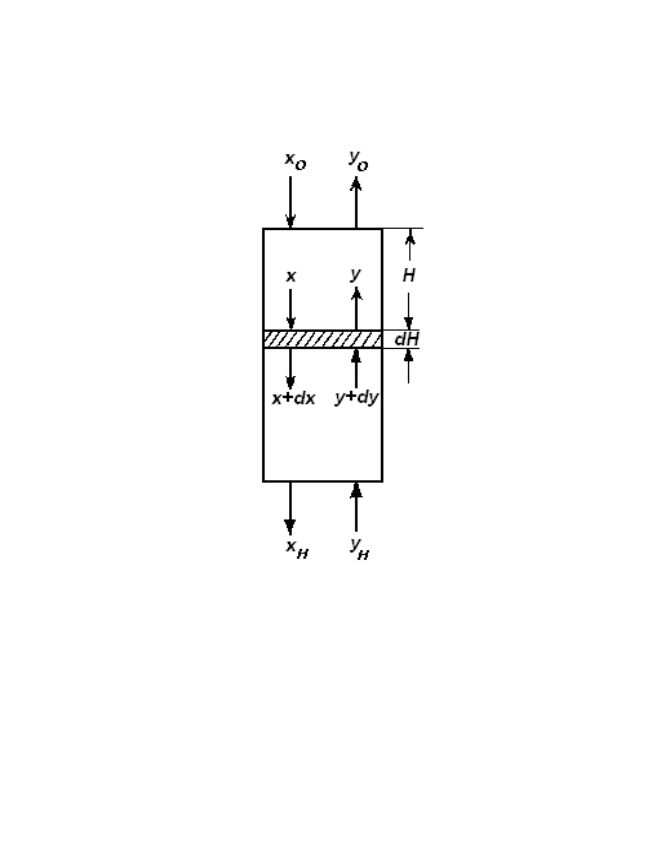
Экстрактор. Рассмотрим еще один объект с распределенными

параметрами.

Пусть имеется экстракционная колонна (рис. 8.8), в верхнюю

часть которой подается раствор, подлежащий экстрагированию, а в

нижнюю часть подводится растворитель.

Рис.8.8. Экстракционная колонна как объект управления

Так как их плотности различны, то раствор в виде сплошной

фазы движется вниз, а растворитель в виде дисперсной фазы

поднимается вверх. В результате массообмена экстрагируемое

вещество переходит из сплошной фазы в дисперсную.

Допустим, что скорости фаз, коэффициент равновесия

распределения постоянны и продольное перемешивание отсутствуют.

Уравнение материального баланса для сплошной фазы в переходном

режиме на элементарном участке колонны высотой dH можно

записать в следующем виде:

Фафурин В.А., Терюшов И.Н. Автоматизация технологических процессов и производств

Подождите немного. Документ загружается.