Фафурин В.А., Терюшов И.Н. Автоматизация технологических процессов и производств

Подождите немного. Документ загружается.

6. Нахождение уравнений динамики и передаточных

функции объекта по его временным (переходным)

характеристикам

Нахождение уравнения объекта по его временной

характеристике

Для получения необходимых исходных данных при расчете

системы автоматического регулирования необходимо найти математи-

ческие выражения экспериментально найденных временных

характеристик. Этими выражениями будут дифференциальные

уравнения объектов, так как временная характеристика представляет

собой не что иное, как графическое изображение результата,

полученного из решения дифференциального уравнения.

В настоящее время имеется несколько методов нахождения диф-

ференциальных уравнений объектов по известным временным харак-

теристикам. Однако ввиду сложности задачи все эти методы являются

приближенными.

Временным характеристикам сложных объектов, очевидно, бу-

дут соответствовать обыкновенные дифференциальные уравнения

высоких порядков или уравнения с частными производными, что

значительно усложняет расчеты. Иногда оказывается возможным

отыскать линейное дифференциальное уравнение с постоянными

коэффициентами невысокого порядка, решение которого с достаточ-

ной точностью соответствует экспериментально снятой кривой.

Рассмотрим некоторые методы аппроксимации.

Большое число простых объектов можно описать дифференциаль-

ными уравнениями первого порядка вида

ВХВЫХ

ВЫХ

kхх

T 



(126)

В этом случае дифференциальное уравнение будет полностью

определенно, если известны коэффициент усиления k и постоянная

времени Т. Решение уравнения (126) представляет собой экспоненту

и записывается в виде

 

T/t

ВХВЫХ

е1хkх





(127)

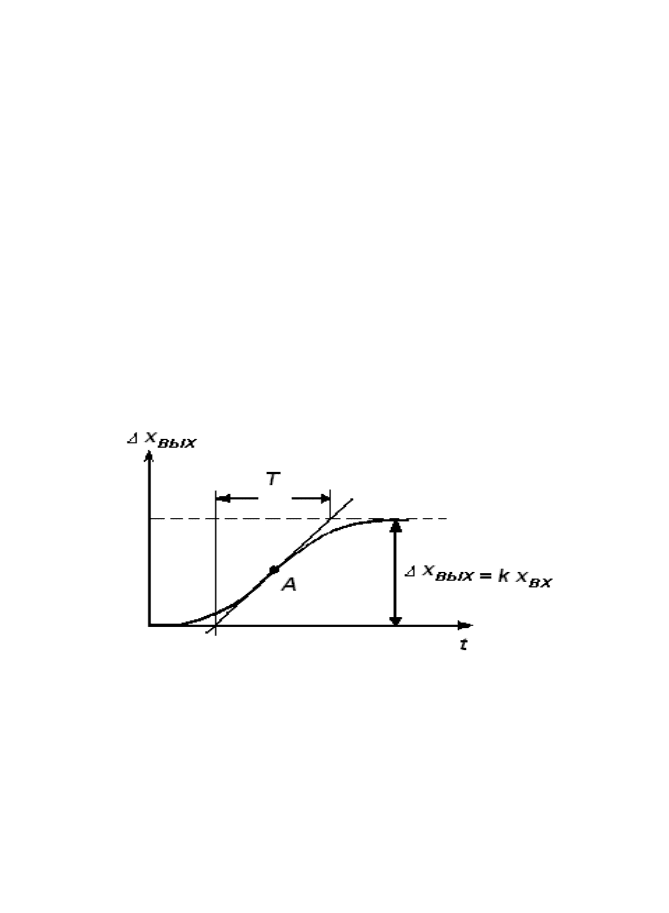
Таким образом, если экспериментально полученная кривая пред-

ставляет собой экспоненту или близка к ней, то непосредственно из

этой кривой можно получить параметры k и Т (см. рис.8.14). Для

проверки удовлетворительности аппроксимации по найденным зна-

чениям k и Т нужно построить кривую, подставив полученные зна-

чения k и Т в уравнение (127). Если расхождения между построенной

кривой и экспериментально снятой временной характеристикой

незначительны (до 5%), то аппроксимацию следует считать

удовлетворительной. В случае же больших расхождений можно

несколько изменить значение постоянной времени Т в ту или иную

сторону и еще раз построить кривую при новом значении Т. После

двух-трех таких изменений можно получить достаточное совпадение.

На точность определения величины Т влияет правильность проведения

касательной к кривой в начальной или любой другой точке.

Рис.8.14. Временная характеристика простого

(одноемкостного) объекта: А – точка перегиба; ∆Х

ВЫХ

– выходная

(регулируемая) координата объекта; ∆Х

ВХ

– входное (возмущающая)

воздействие; k=∆Х

ВЫХ

/∆Х

ВХ

– коэффициент усиления объекта (при

∆Х

ВХ

=1, k=∆Х

ВЫХ

)

Если же кривая имеет вид, показанный на рис. 8.15,а, то

исследуемый объект, относится к сложным объектам и будет

аппроксимироваться дифференциальным уравнением более высокого

порядка.

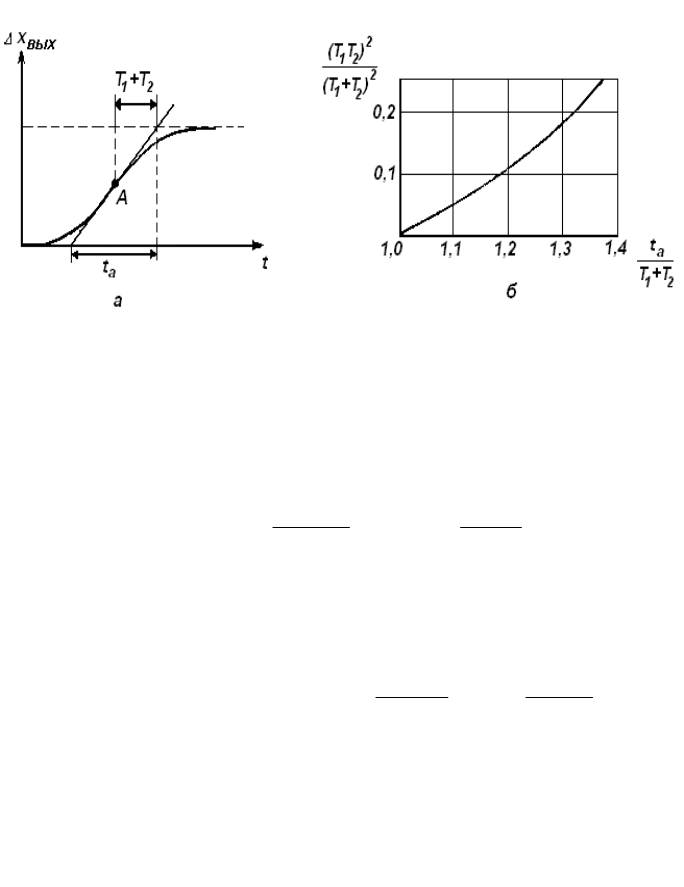
Рис.8.15. Временная характеристика сложного

(многоемкостного) объекта (а) и график для определения Т

и Т

(б)

В этом случае в первом приближении следует попытаться описать

данную кривую дифференциальным уравнением второго порядка

вида

 

ВХВЫХ

ВЫХ

kхх

ТТ

ТT 







(128)

Здесь задача сводится к определению суммы Т

+Т

произведения и Т

постоянных времени при известном коэффициенте

усиления k. Решением уравнения будет выражение



















T/t

ВХВЫХ

ТТ

1хkх

(129)

Проведем касательную к временной характеристике (рис.8.15,а)

в точке перегиба А и отметим отрезки времени t

и Т

+ Т

. Значение

+Т

берем из графика временной характеристики, а величину Т

определяем по вспомогательному графику (рис.8.15,б) в зависимости

от значений t

и Т

+Т

После определения коэффициентов рекомендуется по решению

уравнения (129) построить кривую и сравнить ее с исходной

(экспериментально снятой). При хорошем совпадении найденные

значения коэффициентов можно принять за параметры объекта. В

большом числе случаев подобная аппроксимация дает удовлетво-

рительные результаты.

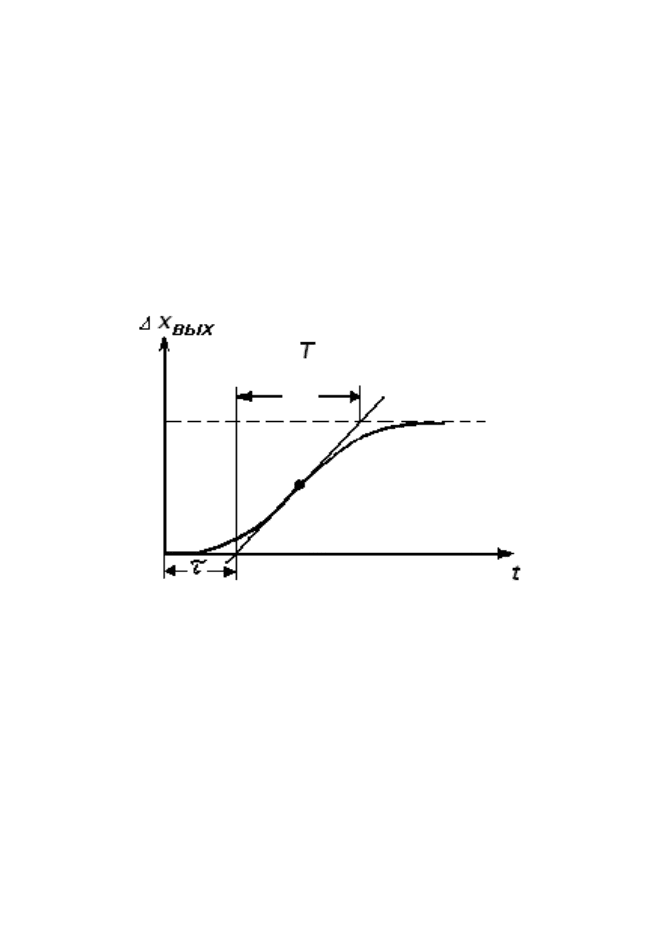
Иногда сложные объекты удается представить в виде простого

объекта с чистым запаздыванием τ (рис. 8.16). Как подтверждает

практика, большинство объектов с распределенными параметрами

можно с достаточной для расчетов точностью описать уравнениями

третьего и четвертого порядков с запаздыванием или без запаздывания.

Рис.8.16. К замене сложного объекта простым с чистым

запаздыванием

Общим недостатком рассмотренных выше экспериментальных

методов определения математических моделей объектов является

искусственное изменение входных величин, что при нормальной

работе технологических установок часто нежелательно, так как это

приводит к нарушению нормального режима работы объекта.

В литературе [4] приводится методы более точной

аппроксимации динамических свойств объектов. Например

устойчивые объекты второго порядка с запаздыванием или без него,

временные характеристики которых имеют S - образную форму,

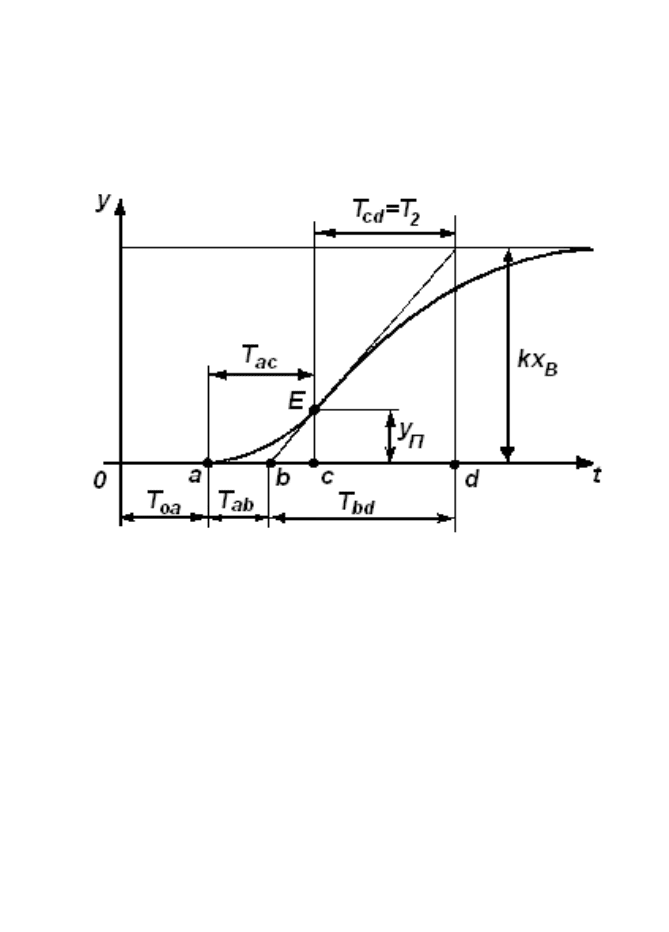
можно математически описать следующим образом. Непосредственно

по графику временной характеристики находят значение

коэффициента усиления объекта

x/kxk 

и времени

действительного запаздывания

, если оно есть, по отрезку

 

oad

Tτoa 

, (см. рис. 8.17).

Рис.8.17. Нахождение постоянных времени объекта по S –

образной временной характеристики

Для определения же постоянных T

и Т

к точке перегиба Е

временной характеристики проводят касательную до пересечения с

осью абсцисс и горизонталью, ордината которой равна

. На этих

горизонтальных прямых откладывают подкасательные T

и T

определяют их величины. Отрезок сd численно равен постоянной

= T

). Постоянную же T

находят по отношению Т

используя зависимость, приведенную на рис. 8.18. Отметим, что S -

образные кривые описываются уравнением устойчивого объекта 2–го

порядка только при соблюдении условия Т



1,4.

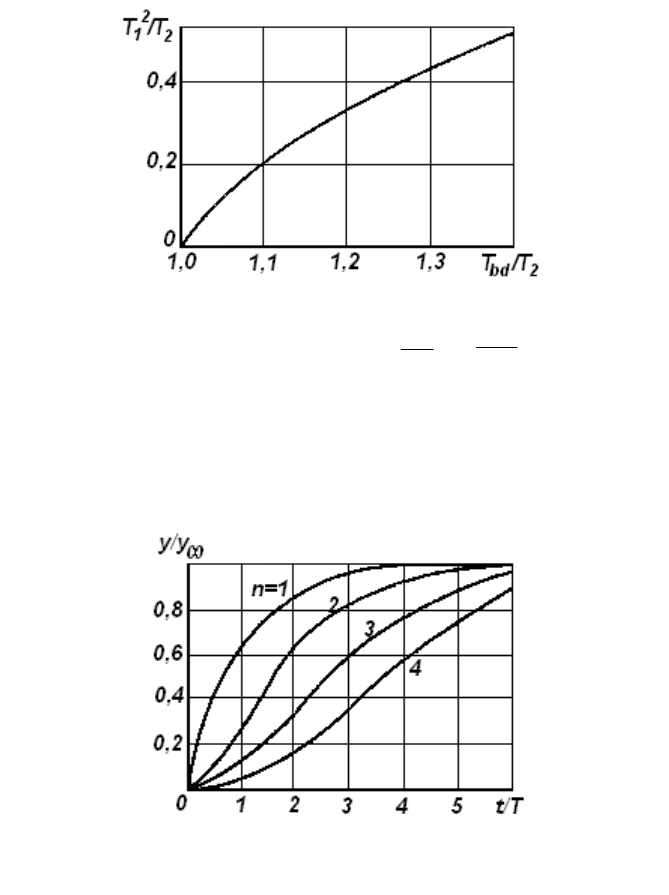
Рис.8.18. Зависимость постоянной

от

При нарушении этого соотношения, экспериментально

полученные S - образные характеристики могут быть описаны

уравнениями более высокого порядка. В качестве примера на рис.8.19

приведены переходные характеристики устойчивых объектов 1- 4–го

порядков.

Рис.8.19. Переходные характеристики объектов n–го порядка

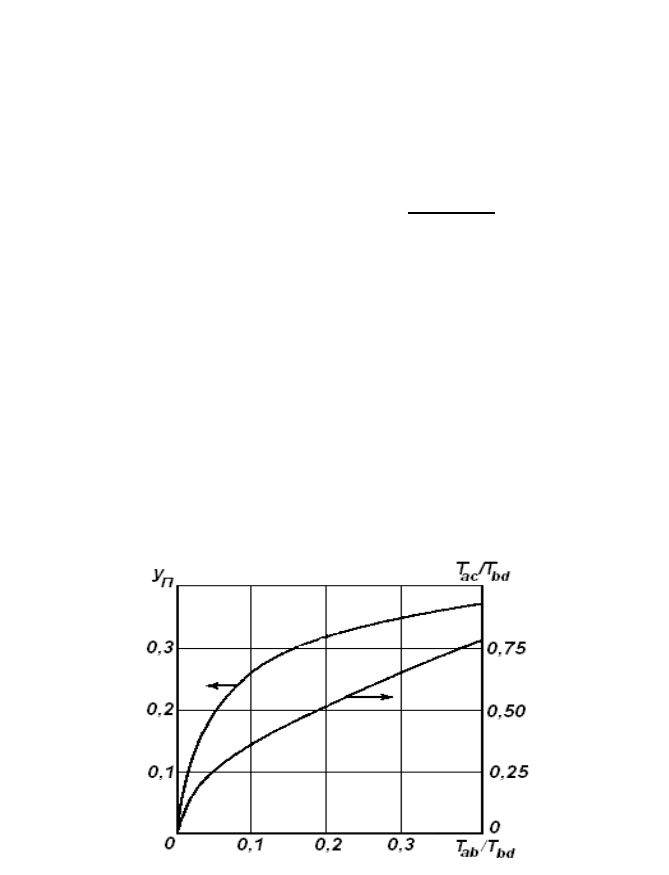
При определении численных значений свойств объектов 3–го и более

высоких порядков по переходным характеристикам последние

аппроксимируют цепочкой последовательно соединенных одного или

нескольких апериодических звеньев 1–го порядка, имеющих

одинаковые постоянные времени Т, и звеном запаздывания, условное

время которого равно

. Передаточная функция такого соединения

запишется в виде:

 

τp

1Tp







(130)

где n=1,2,3,… – число апериодических звеньев.

Сначала экспериментально полученную S - образную

переходную обрабатывают так, как это показано на рис.8.17. Далее

находят величины Т

и Т

и по ним определяют отношение Т

/Т

Затем, используя данные таблицы 8.2, устанавливают порядок

объекта n.

При проведении касательной в точке перегиба кривой

переходной характеристики учитывают, что координаты точки Е и

отношение отрезков Т

/Т

связаны между собой зависимостями,

приведенными на рис.8.20. Это облегчает нахождение точки перегиба

и позволяет скорректировать ее местоположение.

Рис.8.20. Зависимость координаты точки перегиба S–образной

переходной характеристики от отношения Т

Если отношение Т

/Т

с заданной точностью равно табличному

значению, то объект соответствует определенному порядку. Если же

оно отличается от имеющегося в таблице, то порядок объекта

устанавливают по ближайшему меньшему табличному значению Т

и принимают, что передаточная функция описывается равенством

(130)

. При

/Т

< 0,104 порядок объекта равен единице (n=1), а

величины Т и

находят по переходной характеристике:

abybd

TτTT 

Если порядок объекта выше единицы, то сначала определяют

постоянные времени входящих в него апериодических звеньев.

T 

(131)

а затем вычисляют значение времени запаздывания τ

Tkτ



. (132)

Числовые значения постоянных k

и k

при известном порядке

объекта приведены в таблице 8.2.

Таблица 8.2

Данные для определения порядка объекта и параметров его

передаточной функции

bdab

T/T

n k

0,000

0,104

0,218

0,319

0,410

1,000

2,718

3,695

4,463

5,119

0,000

0,282

0,805

1,425

2,100

Условное время запаздывания объекта

находят по равенству

1aby

τTτ 

. (133)

Если на экспериментальной временной характеристике имеется

участок запаздывания оа, то это экспериментально найденное время

запаздывания

объекта можно определить по равенству

τττ 

, (134)

а для объектов 2-го порядка – по равенству

1yd

ττττ 

. (135)

Коэффициент усиления объекта k

находят по отношению

POP

TOT









. (136)

В. Я. Ротач в монографии [5] рассматривает хорошо

зарекомендовавший себя метод, согласно которому

аппроксимирующая передаточная функция объекта представляется в

виде

 

  

τр

1рТ1pT

Ке







(137)

где Т

, Т

, k, τ – соответственно постоянные времени, коэффициент

передачи и запаздывания в объекте; n - показатель, определяющий

порядок знаменателя передаточной функции.

Критерием приближения (адекватности) являются требование

совпадения аппроксимируемой h(t) и аппроксимирующей h

(t)

характеристик в точках t=0, t=



и точке их перегиба Е (см.

рис.8.16), определяемой из условия h(t)=0. Кроме того, в точке

перегиба эти характеристики должны иметь одинаковый наклон.

 

max

tdh















Таким образом, критерий приближения имеет следующий вид:

   

.thth

;thth

;hh

;0h0h

ППa

уст,a



(138)

Для определения производной h(t) переходной характеристики

h(t) в точке Е, где эта характеристика имеет максимальный наклон,

проводится касательная ab и определяется длина отрезка Т

заключенного между точками пересечения этой касательной с осью

абсцисс и линией установившегося значения характеристики h

уст

Приняв, кроме того, обозначение b=h(t

)/h

уст

, критерий

приближения можно переписать следующим образом:

   

 

   

thth

;hh

;0h0h

уста,

Пa

уст,a





(139)

Условия (139) позволяют найти численные значения

постоянных времени

1n,1i,T



, величину t

ПА

и запаздывание

ПАП

ttτ 

аппроксимирующий передаточной функцией (137).

Определение параметров модели

Расчеты параметров

1n,1i,T



, и

 

ПА

tτ 

, входящий в

(137), удобно проводить с помощью таблиц (8.3, 8.4, 8.5, 8.6),

полученных из условий (139) [5].

Порядок использования этих таблиц.

1. По переходной характеристике объекта (см. рис. 8.21)

определяют исходные данные для аппроксимации: h(t

), h

уст

, t

, Т

2. В зависимости от полученного значения b= h(t

)/h

уст

выбирают величину n, определяющую порядок аппроксимирующий

передаточной функции (137).