Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

Compendium

C.1 Basic Algebraic Structures

See for instance [1].

Monoid ð M; Þ or shortly M:

• g

 g

2 M for all g

, g

2 M,

• (g

 g

)  g

= g

 (g

 g

• e 2 M with e  g = g  e = g for all g 2 M, (frequent notation e =:1)

Group (G, )orG:

• (G, ) is a monoid,

• g

-1

2 G with g  g

-1

= g

-1

 g = e for all g 2 G.

Abelian (commutative) group (G, +):

• g

+ g

= g

+ g

, e =: 0.

Ring (K,+,)orK (with unity):

• (K, +) is an Abelian group with e =: 0,

• (K, ) is a monoid with e =:1,

• k

 (k

+ k

) = k

 k

+ k

 k

,(k

+ k

)  k

= k

 k

+ k

 k

(distributivity; if 1 = 0 then K = {0}).

Division ring:

• 1 = 0,

• ðK nf0g; Þ is a group.

347

Field

• K is a division ring with commutative multiplication.

(Some authors consider rings without unity of multiplication and call a division

ring also a ﬁeld.)

Module (V, K,+)orV over the ring K (K-module):

• (V, +) is an Abelian group with e =: 0,

• for all a, b 2 K and for all a, b 2 V, aa 2 V holds with

– a(a + b) = aa + ab,

–(a + b)a = aa + ba,

– a(ba) = (a  b)a.

K itself is a special (one-dimensional) module over K.

Vector space over K (K-vector space):

• K is a ﬁeld. (Often K ¼ R or

K ¼ C:)

K itself is a special (one-dimensional) vector space over K.

Algebra (A, K,+,)orA (K-algebra):

• K is a commutative ring (with unity),

• (A, K, +) is a module,

• (A, ) is a monoid, and for all a, b, c 2 A and for all a 2 K

– a  (b + c) = a  b + a  c,(a + b)  c = a  c + b  c,

– a(a  b) = (aa)  b = a  (ab).

itself is a special (one-dimensional) algebra over K.

Associative algebra:

• (a  b)  c = a  (b  c).

Algebra with unity:

• e 2 A with a  e = e  a = a for all a 2 A.

In an associative algebra with unity (A,  ) is a ring.

Commutative algebra:

• a  b = b  a.

348 Compendium

Algebraic homomorphism f :AS? AS

, where f commutes with all algebraic

operations, for instance

f ðg

 g

Þ¼f ðg

Þf ðg

Þ etc.

In cases of modules or vector spaces and algebras, usually only K = K

is of

interest. Homomorphisms of modules or of vector spaces are called linear

mappings or linear functions or linear operators.

Kernel of the homomorphism: Ker f = f

-1

f :AS? AS

is called an algebraic isomorphism,iff and f

-1

are algebraic

homomorphisms. AS and AS

are called algebraically isomorphic in this case:

AS  AS

A homomorphism f :AS? AS is called Endomorphism (f 2 End (AS)).

An isomorphism f :AS? AS is called Automorphism (f 2 Aut (AS)).

AS is called a sub-AS of AS

, if it is isomorphic to a part of AS

. For every

homomorphism f :AS? AS

, f(AS) is a sub-AS of AS

Let S be part of an AS. The intersection of all sub-AS containing S is called the

sub-AS generated by S. A part S generating a module is said to be linearly

independent if every ﬁnite subset of S is linearly independent; a linearly

independent set S generating a module is called its algebraic base. The

cardinality of an algebraic base of a vector space is its algebraic dimension.

Invariant subgroup (normal subgroup) H of G:

H is a subgroup of G and

gHg

1

 H for all g 2 G:

In this case there exists a homomorphism f : G ? G

with Ker f = H and

f (G) = G

is the quotient group or factor group G= H.

For any g

2 G=H; f

1

ðg

ÞG is called coset of H in G.

If G

¼ G=H is also an invariant subgroup of G, then G = H 9 G

is a direct

product of groups, that is,

G ¼ g ¼ g

 g

¼ g

 g

2 H; g

2 G

; g  g

¼ðg

 g

Þðg

 g



Ideal ((twosided) invariant subring) I of a ring K:

I is a subring of K and

aI  I; Ia  I for all a 2 K:

Compendium 349

In this case there exists a homomorphism f : K ! K

 K

with Ker f = I and

f (K) = K

is the quotient ring (factor ring) K=I.

If K

¼ K=I is also an ideal of K, then K ¼ I  K

is a direct sum of rings, that

is,

K ¼ a ¼ a

þ a

2 I; a

2 K

; a  a

¼ a

 a

þ a

 a



Simple group a group G = {e} that has no non-trivial invariant subgroups, that

is, no invariant subgroups besides G and {e}.

Representation of a group G is a homomorphism D : G ? Aut (S) into the group

of transformations (permutations) of a non-empty set S.

Dðg

 g

Þ¼Dðg

ÞDðg

Þð)DðeÞ¼ Id

Þ:

The adjoint representation Ad : G ? Aut (G) represents g 2 G as the

transformation g

7!gg

1

of G,

Ad ðgÞ : G ! G : g

7! Ad ðgÞg

¼ gg

1

In this case, a common notation is

Ad ðg

1

Þg

¼ g

1

g ¼ðg

; ððg

¼ðg

; ðg

¼ g

Another most important special case of group representation is that S is a

complex vector space V (C-vector space).

Representation of a K-algebra A is a homomorphism D : A ? End(V) into the

K-algebra of endomorphisms of a K-module V, the representation module,

which commutes with the action of K into both algebras:

• D(e)=Id

if A is an algebra with unity,

• D(aa + bb) = aD(a)+bD(b), a, b 2 K, a, b 2 A,

• D(a  b) = D(a)  D(b).

For both groups and algebras there exists always the trivial representation (unit

representation, null representation)

• D(g) = Id

for all g 2 G and

• D(a) = 0 for all a 2 A.

If G(A) itself is a group (algebra) of automorphisms (endomorphisms), then the

identical isomorphism is called the identical representation.

A representation is called faithful, if the representing homomorphism is

injective.

If a group G or an algebra A is represented in a ﬁnite-dimensional vector space

V and V contains an invariant subspace V

, that is, D(g)V

, V

for all g 2 G or

350 Compendium

A, then the representation D is called algebraically reducible, otherwise it is

algebraically irreducible.IfD is reducible, then there exists a suitable basis in

V so that

DðgÞ¼

ðgÞ F

0 D

ðgÞ



for all g 2 G or g 2 A:

If V

¼ V=V

is also invariant, then D ¼ D

 D

is a direct sum of

representations, that is,

DðgÞ¼

ðgÞ 0

0 D

ðgÞ



for all g 2 G or g 2 A:

Two representations D and D

in V and V

are called equivalent, D  D

; if

there is an isomorphism L : V ? V

so that

DðgÞ¼L

1

ðgÞL for all g 2 G or g 2 A:

Schur’s lemma If D is a ﬁnite-dimensional irreducible representation in V, then

each linear operator L in V which commutes with all D(g), g 2 G or A is

proportional to the unit operator, L = k Id

Derivation d Linear mapping d : A ? A of an algebra A to itself obeying the

Leibniz rule d(g

) = d(g

+ g

d(g

) for all g

, g

2 A.

Category A : Consisting of

• a class ObðAÞ ¼ fA; B; C; ...g of objects,

• a class Ar ðAÞ of morphisms (arrows) f, g,... with the properties

– for each pair ðA; BÞ2Ob ðAÞ  Ob ðAÞ there is a set MorðA; BÞ2

ArðAÞ so that the composition rule

Mor ðB; CÞ Mor ðA; BÞ! Mor ðA; CÞ : ðg; f Þ7!g  f

holds,

–ArðAÞ ¼ [

ðA;BÞ

Mor ðA; BÞ is a disjoint union,

– for each A 2 Ob ðAÞ there is Id

[ Mor (A, A) = End (A) with

 f ¼ f ¼ f  Id

for every f 2 Mor ðA; BÞ;

– when it is deﬁned, the composition of morphisms is associative:

ðh  gÞf ¼ h ðg f Þ:

Isomorphism and automorphism have their usual meaning; End (A)is

obviously a monoid with respect to composition, Aut (A) is a group (its

morphisms are called permutations or transformations). Hence there are

group homomorphisms from any group G into Aut (A)ofany category.

Compendium 351

Examples of categories are sets with mappings, various AS with algebraic

homomorphisms, topological spaces with continuous functions, topological AS

with homomorphisms, topological, differentiable, smooth, analytic manifolds

with corresponding mappings, ﬁber spaces with homomorphisms and so on.

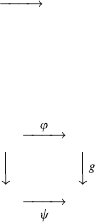
Diagrams For f 2 Mor (A, B) the diagram

is used. If A is a category then its arrows may be taken as objects of a new

category M : Ar ðAÞ ¼ Ob ðMÞ : A morphism f ! g; f ; g 2 Ar ðAÞ of M

is a pair ðu; wÞ so that the following diagram is commutative:

A C

B D

The commutative diagram means w  f ¼ g  u: If B = D and w = Id

are ﬁxed, then a category A

is obtained with morphisms u:

Covariant functor F from category A into category B :

• Ob ðAÞ 3 A ! FðAÞ2 Ob ðBÞ with F(Id

) = Id

F(A)

• Mor ðA; BÞ3f ! Fðf Þ2 Mor ðFðAÞ; FðBÞÞ with F(g  f) = F(g)  F(f).

Instead of F(f) the notation f

is often used: push forward.

A cleaning covariant functor maps a category into a simpler category.

Let S be the category of sets, and let some category A and an object A 2

Ob ðAÞ be ﬁxed. The functor M

: A!Sgiven by

• M

(X) = Mor (A, X) (taken as a set of mappings) for every X 2 Ob ðAÞ;

• M

ðuÞ : Mor ðA; XÞ! Mor ðA; X

Þ : w 7!u  w for every u 2 Mor ð X;

ÞAr ðAÞ

is called a representing covariant functor.

Contravariant functor F from category A into category B :

• Ob ðAÞ 3 A ! FðAÞ2 Ob ðBÞ with F(Id

) = Id

F(A)

• Mor ðA; BÞ3f ! Fðf Þ2 Mor ðFðBÞ; FðAÞÞ with F(g  f) = F(f)F(g).

Instead of F(f) the notation f

is often used: pull back.

Let again some category A and an object A 2 Ob ðAÞ be ﬁxed. The functor

: A!Sgiven by

352 Compendium

• M

(X) = Mor (X, A) (taken as a set of mappings) for every X 2 Ob ðAÞ;

• M

ðuÞ : Mor ðX; AÞ! Mor ðX

; AÞ : w 7!w u for every u 2 Mor ðX

;

XÞ ArðAÞ

is called a representing contravariant functor.

A functor puts isomorphisms into isomorphisms.

Representing functors are used to transfer certain structures on sets to arbitrary

categories. (If e.g. A has a group structure, then Mor (X, A) has also a group

structure by (fg)(x) = f(x)g(x), and M

is a functor from the category A into the

category of groups. Conversely, if Mor (X, A) has some group structure, then, by

the same relation, A has a group structure.)

Complexes of K-modules

• C ¼

r2Z

with C

 C

 C

rþr

is a graded (by r) module (vector space,

algebra) over a ring (ﬁeld) K,

• d ¼fd

jr 2 Zg : C ! C

is a graded morphism of degree s, d

: C

? C

r+s

from the graded module C into the graded module C

• a complex (C, d) consists of a graded K-module C and a graded

endomorphism d : C ? C of degree 1,

• a morphism f :(C, d) ? (C

, d

) of complexes of degree s is a graded

morphism for which the diagram

r−1

r−1+s

r−1

r−1+s

r+s

commutes.

Homology and cohomology of a complex (C, d):

• Z

= Ker d

is the module of r-cocycles,

• B

¼ Im d

r1

is the module of r-coboundaries,

• H

¼ Z

is the rth cohomology module of the cohomology H(C) of the

complex (C, d).

• if f :(C, d) ? (C

, d

) is a graded morphism of degree s, then it is pushed

forward to a canonical homomorphism f

: H(C) ? H(C

) of degree s of their

cohomologies,

• homology is the same for a complex (C, d) with d of degree -1; this is

included into the above scheme by the mapping r ? -r.

Exact sequences

• a sequence of morphisms of AS,

!A ! B !

Compendium 353

is called exact, if the image of each morphism in the sequence is the kernel of

the next,

• 0 ! G!

H means that f is injective,

• G!

H ! 0 means that f is surjective,

• 0 ! G!

H ! 0 means that f is an isomorphism,

• for Abelian groups or modules, the sequence

0 ! H ! G ! G=H ! 0

is called a short exact sequences,

• let

0 !ðC; d

Þ!

ðD; d

Þ!

ðE; d

Þ!0

be a short exact sequence of graded morphisms, without loss of generality of

degree 0, of complexes; then there exists canonically a graded morphism

HðEÞ!

HðCÞ

of degree 1 of their cohomologies, so that the long sequence

!

ðCÞ!



ðDÞ!



ðEÞ

!

rþ1

ðCÞ!



rþ1

ðDÞ!



rþ1

ðEÞ!



ð3:124Þ

is exact (‘snake lemma’).

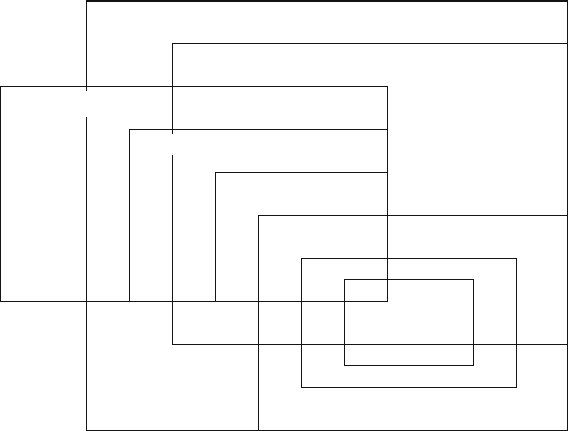
vector spaces

locally convex vector spaces

topological spaces

metric spaces

Lie groups

ﬁber bundles

manifolds

normed vector spaces

Schematic interrelation of various to

olo

ical s

aces

354 Compendium

C.2 Basic Topological (Analytic) Structures

See for instance [2]; for homotopy groups, [3].

Topological space ðX; TÞor shortly X:

• T is the set of open subsets of X; [ 2T; X 2T;

• Every union of sets T 2T belongs to T ;

• Every intersection of ﬁnitely many sets T 2T belongs to T ;

T is called the topology on X.

Coarser (ﬁner) topology T

on X : T

T; ðT

TÞ: Discrete topology: T¼

PðXÞðPðXÞ : set of all subsets of X). Trivial topology: T¼f[; Xg:

Closed sets C : C ¼ XnU for some U 2T: In the discrete topology every set is

open-closed. The closure

A of a set A , X is the smallest closed set containing

A; the interior A



is the largest open set contained in A. The boundary oA of

A is

A n A



. A is dense in X,ifX ¼ A; A is nowhere dense in X,ifðAÞ



¼ [. X is

separable,ifX ¼

A for some countable A.

Neighborhood of a point x 2 X : UðxÞ2T; x 2 UðxÞ: A neighborhood of a set is

a neighborhood of every point of the set. Inner point x of A , X: U(x) , A for

some neighborhood UðxÞ; x 2 A



: Point of closure x of A , X: A \ U(x) = [

for any neighborhood UðxÞ; x 2

A: Cluster point x of A  X : ðA nfxgÞ \

UðxÞ 6¼ [ for any neighborhood U(x).

Relative topology T

on A , X related to ðX; TÞ: T

¼fA \T jT 2Tg:

Hausdorff topology Every pair of points x = y 2 X has a pair of disjoint

neighborhoods, U(x) \ U(y) = [. Then, every one point set {x} is closed. The

limes of a sequence of points is unique if it exists. Regular topology: Every

non-empty open set contains the closure of another non-empty open set.

Normal topology: Every one point set is closed and every pair of disjoint

closed sets has a pair of disjoint neighborhoods.

Continuous function F: X ? Y from a topological space ðX; TÞinto a topological

space ðY; UÞ : For every U 2U; F

1

ðUÞ2T:

Homeomorphism F: X ? Y: a bicontinuous bijection F: F

-1

exists and F and F

-1

are continuous. X and Y are homeomorphic, X * Y, if a homeomorphism F:

X ? Y exists. A topological invariant is a property preserved under

homeomorphisms.

Compendium 355

Base of the topology T : Family BT; so that every T 2T is a union of sets

B 2B: Neighborhood base BðxÞ at x 2 X: Every B 2BðxÞ is a neighborhood

of x, and for every neighborhood U(x) there is a B 2BðxÞ with B , U(x). X is

ﬁrst countable, if every x 2 X has a countable neighborhood base, X is second

countable if it has a countable base of topology.

Product topology ðX; TÞ¼ð

a2A

; f

a2A

gÞ where U

and U

= X

for all but ﬁnitely many U

(Tychonoff’s product; the set

a2A

is the set of

all functions F : a 7!x

2 X

on A.)

Quotient topology The ﬁnest topology on X=R (R is an equivalence relation in

X) in which the canonical projection p: X ! X=R is continuous. (U 2 X=R is

open, iff p

-1

(U) 2 X is open.)

Metric topology with base B¼fB

1=n

ðxÞjx 2 X; 0\n 2 Zg of open balls

ðxÞ¼fx

jdðx; x

Þ\r; r [ 0g; d : X  X ! R

is the distance function:

• d(x, y) = 0iffx = y,

• d(x, y) = d(y, x),

• d(x, z) B d(x, y)+d(y, z) (triangle inequality).

Metrizable space A topological space with topology which has a base of open

balls in some metric d.

Cauchy sequence in a metric space X:{x

} with lim

m;n

dðx

; x

Þ¼0:

Complete metric space X Every Cauchy sequence converges in X. Every

contracting sequence C

. C

. _ of closed balls has a non-empty

intersection.

Topological vector space X over the ﬁeld K : K  X ! X : ðk; xÞ7!kx; X  X !

X : ðx; x

Þ7!x þx

; k 2K; x; x

2 X are continuous. Sum of subsets:

A + B = {x + x

x j2A, x

2 B.If{B

(0)} is a neighborhood base at x = 0,

then {x + B

(0)} is a neighborhood base at x.(x + A =: {x}+A.)

Functional F: X ? K.

Linear independence of a set E , X If

n¼1

holds for any set of N \ ?

distinct x

2 E, then all k

= 0. With arbitrary k

2 K, all possible such linear

combinations with all possible N \ ? form the span span

E of E.Ifspan

E ¼

X; then the cardinality of E is the dimension of X and E forms a base in the

vector space X. X is separable, if it admits a countable base. If E is a base of

X and F is a base of Y, then E [ F taken as a linear independent disjunct sum is

a base of X + Y, the direct sum of the topological vector spaces X and Y with

the product topology; X \ Y = {0}.

356 Compendium