Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.



 d



; l ¼ 1; ...; m;

which after matrix multiplication with w

1

from the right uniquely determines



; tÞ on UðuÞ: h

Now, let M be a Riemannian manifold and consider the Riemannian geometry

provided by the Riemannian connection on M. Let u 2 M be any point. Modify the

choice of the ﬁxed frame at u from the above proof into an orthonormal frame with

respect to the Riemannian metric tensor: ðX

Þ¼d

. (Compare (9.4, 9.5).)

Then, t acquires the meaning of the arc length of geodesics measured from the point

u, and the frame ﬁeld becomes a local section in the orthonormal frame bundle

ðMÞ. With respect to the corresponding normal coordinates v

¼ t



, a tangent

vector onM at u,that is, atv ¼ 0 isX

¼ o= o t ¼

ðov

=otÞðo=ov

Þ¼



ðo=ov

Þ.

By the above choice, g

ðuÞ¼gðX

; X

Þ¼d

, or, with hh

; X

i¼d

g ¼

i¼1

 h

. Since, by deﬁnition of a Riemannian connection, g does not

change upon parallel transport, the last expression holds on the whole normal

coordinate neighborhood UðuÞ. (Caution: h

6¼ dv

in general on UðuÞ and g is not

 dv

.) Moreover, for the local connection forms themselves in these normal

coordinates x

þ x

¼ 0 (see text after the second formulation of the Fundamental

Theorem of Riemannian Geometry in the previous section). There are m standard

horizontal vector ﬁelds X

; i ¼ 1; ...; m whose values at point u are X

and which on

UðuÞ hence make up the above frame ﬁeld, and dual to them there are m components

of the canonical one form so that hh

; X

i¼d

(p. 234) yielding

¼ g

ðh

ð9:46Þ

for the element of the arc length. The symmetric 2-form (9.46) is called the ﬁrst

fundamental form of a Riemannian geometry. It is obviously covariant under

OðmÞ-transformations of the structure group of the orthonormal frame bundle

ðMÞ. The corresponding natural deﬁnition of a volume form of a Riemannian

geometry is

s ¼ h

^^h

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

jdet gj

^^dx

; ð9:47Þ

where the ﬁrst expression is invariant under SOðmÞ-transformations and only

changes sign under OðmÞ-transformations with determinant 1 of the transfor-

mation matrix (and hence switching orientation of the frame), while the second

expression holds in any local coordinate system as was shown for (5.84).

As in the previous proof on p. 316, h



dt þ



, where



¼ 1;



t¼0

0; ðo



=otÞ

t¼0

¼ d



and



does not contain dt. The element of the arc length in

UðuÞ is obtained as

¼ dt

þ 2dt



9.4 Geodesic Normal Coordinates 317

However,



t¼0

¼ 0, and by the ﬁrst equality (9.44), ð o = o tÞ







¼ 0; the ﬁrst sum vanishes because of the normalization of



Þ and the second because of the skew-symmetry of x

. Hence,



¼ 0 on

UðuÞ, and

¼ dt



;



¼ td



; tÞd



;





t¼0

¼ 0;





t¼0

¼ 0:

ð9:48Þ

In particular, (9.48) implies ðdtj



Þ¼0; i ¼ 1; ...; m on UðuÞ. Observe that

m 1 linearly independent linear combinations of the m (linearly dependent

because of the linear dependence of the d



) cotangent vectors



span locally

(inﬁnitesimally) the hypersurface t

ðv

¼ const., while dt is a cotangent

vector on the geodesic through u. (Since with respect to normal coordinates

¼ d

, tangent vectors X with components X

and cotangent vectors r with

components r

¼ g

¼ X

are equivalent.)

In a Riemannian geometry, in every normal coordinate neighborhood of a point

u, geodesics through u are orthogonal to hypersurfaces (hyperspheres)

ðv

¼ const.

It is easy now to prove that

in a Riemannian geometry M there exists at every point u 2 M a normal

coordinate neighborhood W such that (i) every point u

2 W has a normal

coordinate neighborhood that contains W and (ii) the geodesic curve that con-

nects u and u

2 W is the unique shortest curve in W connecting these two points.

Proof (i) was already proved to hold true for any linear connection manifold.

Hence, it holds in particular for the Riemannian connection of a Riemannian

manifold.

To prove (ii), let W ¼ U



ðuÞ with sufﬁciently small  be the neighborhood

(9.41)ofu with respect to normal coordinates v

at u. Pick u

2 W, and let

: v



¼ const.; 0 t t

be the geodesic connecting u with u

, t

being

its arc length, that is, u

has normal coordinates



. Let C : v

¼ v

ðtÞ be any curve

in W from u to u

with parameter t, without loss of generality chosen to be the

geodesic arc length from u to the point u

2 C with normal coordinates v

ðtÞ. Then,

the arc length of C is

s ¼

ds ¼



1=2



dt ¼ t

318 9 Riemannian Geometry

Hence, s cannot be shorter then t

, and s ¼ t

implies



¼ 0 for i ¼ 1; ...; m.In

view of (9.48), this means that for 0 t t



; tÞ



¼ 0;

while d



is independent of t, and lim

t!0



; tÞ=tÞ¼0 due to the initial

conditions of (9.48). Hence, it follows d



¼ 0 and



¼ const. for 0 t t

, which

means that C is the unique geodesic C

connecting u and u

: h

In the normal coordinate neighborhood W of this theorem the distance (9.8)

from u to u

equals the arc length of the unique geodesic connecting the two points.

This is in general not true globally; for instance, on a sphere geodesics are the

great circles, and for two points on a great circle not being antipodes there are two

arcs of different length connecting them.

Sufﬁciently small -ball normal coordinate neighborhoods have important

properties in relation to geodesics which are analogues of corresponding properties

of balls of any radius in Euclidean space in relation to straight lines. This section is

concluded with their consideration.

Let UðuÞ be a normal coordinate neighborhood of u in a Riemannian geometry

and let

¼ x

i¼1

ðv

ðxÞÞ

¼ q



()

ð9:49Þ

be a hypersphere of radius q in UðuÞ. Then, (i) there exists a positive number  so

that for any q; 0\q\, any geodesic curve v

ðsÞ tangent to S

at s ¼ 0 is outside

for small values of the curve parameter s and has s ¼ 0 as its only one point in

common with S

in a neighborhood of s ¼ 0; (ii) there exists a positive q such that

for any two points in the q-ball neighborhood U

ðuÞ of u there is a unique

geodesic in U

ðuÞ connecting the two points.

A neighborhood of u having the two properties of U

ðuÞ of this theorem is

called a geodesic convex neighborhood; the theorem states the existence of a

geodesic convex neighborhood of every point in a Riemannian geometry.

Proof Consider the real function Fðv

; ...; v

Þ¼ð1=2Þð

ðv

 q

Þ. Then, S

is determined by Fðv

ðxÞÞ ¼ 0. Let C : v

ðsÞ be a geodesic through u

2 S

and

being tangent to S

at this point, with curve parameter s passing through zero at u

Since it was already shown that a geodesic C

: v

¼ tv

ðs ¼ 0Þ from u to u

orthogonal to S

at u

, the latter condition amounts to saying that C is orthogonal to

at u

. Denote tangent vectors to these geodesics at u

by X

and X

, respec-

tively. Their orthogonality spells

0 ¼ðX

Þ¼

i¼1

ðs ¼ 0Þ



s¼0

9.4 Geodesic Normal Coordinates 319

This implies

dFðv

ðsÞÞ



s¼0

ð0Þ



s¼0

¼ 0;

Fðv

ðsÞÞ



s¼0



ijk

ð0ÞC

ðv

ð0ÞÞ

;

where all derivatives are taken for s ¼ 0 and (9.36) was used in the second

derivative. Therefore,

Fðv

ðsÞÞ ¼





ijk

ð0ÞC

ðv

ð0ÞÞ

þ oðs

Þ:

Since with respect to normal coordinates C

ð0Þ¼0, its value at u

, that is, for

ð0Þ can be made arbitrarily small by taking a small value of q. Therefore, for

small enough q, Fðv

ðsÞÞ is zero for s ¼ 0 and strictly positive for small non-zero

values of s. This proves (i).

Next, chose q =4 where  is the value of statement (i). For the distance of

two points u

; u

2 U

ðuÞ the triangle inequality yields dðu

; u

Þ

dðu; u

Þþdðu; u

Þ\2q =2. Hence, u

2 U

=2

ðu

Þ, and for any x 2 U

=2

ðu

Þ it

holds that dðu; xÞdðu; u

Þþdðu

; xÞ\3=4. According to the theorem visual-

ized in Fig. 9.2, U



ðuÞ may be chosen such that every point u

2 U



ðuÞ has a

normal coordinate neighborhood Uðu

Þ that contains U



ðuÞ. Then,

=2

ðu

ÞU



ðuÞUðu

Þ, and normal coordinates at u

can be used in U

=2

ðu

Þ.

By the previous theorem above there is a unique geodesic C connecting u

with u

whose arc length is dðu

; u

Þ, and for any intermediate point x on this geodesic

dðu

; xÞdð u

; u

Þ. C  U

=2

ðu

ÞU



ðuÞ, and hence dðu; xÞ is bounded by  on

C, while dðu; u

Þ and dðu; u

Þ are less than q =4. Suppose that the maximum of

dðu; xÞ on C is at an intermediate point x

and is equal to d

\. Then, C is tangent

to S

and hence by virtue of (i) d

is a local minimum on C. This contradiction

proves dðu; xÞ\q, that is, C lies in U

ðuÞ: h

Again, in that last theorem no statement is made on the global behavior of

geodesics. For large enough values of the curve parameter s, a geodesic tangent to

at u

may return arbitrarily close to u

and cross S

, and likewise two points in

ðuÞ may in addition to the claimed unique geodesic in U

ðuÞ be connected by a

geodesic (maybe the same) that intermediately leaves U

ðuÞ; think for instance

again of a great circle on a spherical manifold.

Modifying the last proof in such a way that one works only with Euclidean

distances in coordinate neighborhoods U, the existence of geodesic convex

neighborhoods can be proved for any linear connection manifold independent of

the presence of a Riemannian metric [3].

From the above analysis it is also clear that a curve x

¼ x

ðtÞ in a linear

connection space M is a geodesic, iff it is the projection on M of an integral curve

320 9 Riemannian Geometry

of a standard horizontal vector ﬁeld on the frame bundle LðMÞ. Recall, that every

integral curve of a vector ﬁeld is contained in a maximal integral curve

corresponding to some open interval a\t\b of the parameter t of the local

1-parameter group. A linear connection is called a complete linear connection,if

every geodesic with parameter t may be continued to a geodesic for 1\t\1:

9.5 Sectional Curvature

For the case of a Riemannian geometry a more detailed geometric meaning of the

curvature tensor can now be found.

The Riemannian curvature tensor (9.33), as any tensor of type ð 0; 4Þ may be

considered as a quadrilinear function R : T

ðMÞT

ðMÞ!R:

RðW; X; Y; ZÞ¼hR; W  X  Y  Zi¼R

ijkl

: ð9:50Þ

In particular, in arbitrary local coordinates,

ijkl

¼ R

;



: ð9:51Þ

The properties (9.34) transfer to corresponding properties of the quadrilinear

function:

RðW; X; Y; ZÞ¼RðX; W; Y; ZÞ¼RðW; X; Z; YÞ;

RðW; X; Y; ZÞþRðW; Y; Z; XÞþRð W; Z; X; YÞ¼0;

RðW; X; Y; ZÞ¼RðY; Z; W; XÞ:

ð9:52Þ

On p. 311 f it was shown that the third line of (

9.34) follows from the ﬁrst two

lines. Hence, the same is true for (9.52). Moreover, let R and R

be two quadri-

linear functions on some vector space V, having the properties of the ﬁrst two lines

of (9.52). If

RðX; Y; X; YÞ¼R

ðX; Y; X; YÞ for all X; Y 2 V; ð9:53Þ

then R ¼ R

. Indeed, consider R

¼ R

 R and suppose R

ðX; Y; X; YÞ¼0 for all

X; Y 2 V. Then, for all Z 2 V, 0 ¼ R

ðX; Y þ Z; X; Y þ ZÞ¼R

ðX; Y; X; ZÞþ

ðX; Z; X; YÞ¼2R

ðX; Y; X; ZÞ due to the third line of (9.52) which follows from

the ﬁrst two lines. Hence, R

ðX; Y; X; ZÞ¼0 for all X; Y; Z 2 V and therefore

0 ¼R

ðW þY; X; W þY;ZÞ¼R

ðW; X; Y; ZÞþR

ðY; X; W; ZÞ¼R

ðW; X; Y; ZÞþ

ðW; Z; Y; XÞ¼R

ðW; X; Y; ZÞR

ðW; Z; X; YÞ, where in the third equality the

third line of (9.52) was used and in the last equality the ﬁrst line. Thus, also

ðW; X; Y; ZÞ¼R

ðW; Z; X; YÞ and, by simply renaming X; Y;Z into Y; Z; X,

ðW; Y; Z; XÞ¼R

ðW; X; Y; ZÞ for all W; X; Y; Z 2 V. From these last two rela-

tions, 3R

ðW; X; Y; ZÞ¼R

ðW; X; Y; ZÞþR

ðW; Y; Z; XÞþR

ðW; Z; X; YÞ¼0 for

all W; X; Y; Z 2 V and hence R ¼R

9.4 Geodesic Normal Coordinates 321

A quadrilinear function determined solely by the metric tensor (9.3), which has

the same properties (9.52), is

GðW; X; Y; ZÞ¼GðW; YÞGðX; ZÞGðW; ZÞGðX; YÞ: ð9:54Þ

For X; Y 2 T

ðMÞ,

GðX; Y; X; YÞ¼jXj

jYj

ðXj YÞ

¼jXjjYjsin \ðX; YÞðÞ

: ð9:55Þ

This is the square of the area of a parallelepiped spanned by the vectors X and

Y. Let X

; Y

span the same two-dimensional subspace E of T

ðMÞ as X; Y, that is,

ðX

; Y

¼ AðX; YÞ

, where A is a regular ð2 2Þ-matrix, det A 6¼ 0. From the

properties (9.52) it is easily found (exercise) that

RðX

; Y

; X

; Y

Þ¼ðdet AÞ

RðX; Y; X; YÞ;

GðX

; Y

; X

; Y

Þ¼ðdet AÞ

GðX; Y; X; YÞ:

Hence, the quotient of R and G is an invariant of E. Its negative is called the

sectional curvature of M at ðx; EÞ:

Kðx; EÞ¼

RðX; Y; X; YÞ

GðX; Y; X; YÞ

: ð9:56Þ

Since G is uniquely deﬁned by the metric tensor, it follows from the above that

the curvature tensor of a Riemannian manifold M at point x is uniquely determined

by the sectional curvatures of all the two-dimensional subspaces of the tangent

space T

ðMÞ:

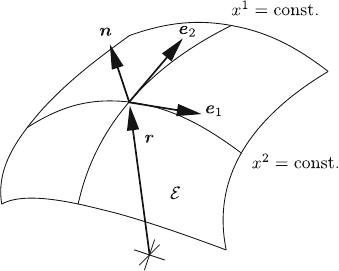
Gauss’ theory of surfaces uses a parameter representation

r ¼ rðx

; x

Þ; r ¼ðr

; r

Þ ð9:57Þ

with parameters x

; x

for a two-dimensional smooth surface E embedded in the three-dimen-

sional Euclidean space R

, with Cartesian coordinates r

(with respect to an orthonormalized base

; a

g, r ¼

). The frame (Fig. 9.3)

; e

; n ¼

 e

; e

 e

6¼ 0; ð9:58Þ

at point rðx

; x

Þ2R

describes the tangent plane on E at point ðx

; x

Þ2Eas the plane spanned

by the vectors e

and e

and having the normal n in R

. In the metric inherited from R

, the

element of arc length on E is given by

ds ¼ e

þ e

;

i¼1

j;k¼1

¼ Eðdx

þ 2Fdx

þ Gðdx

¼ g

;

E ¼

i¼1



; F ¼

i¼1

; G ¼

i¼1



; ðg

Þ¼



ð9:59Þ

The second line is Gauss’ ﬁrst fundamental form of the surface E. The volume form of E

(surface area element, without a deﬁnition of sign of orientation) is

322 9 Riemannian Geometry

jsj¼je

 e

j¼ðje

jje

je

 e

1=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

EG F

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

ð9:60Þ

From dn ¼je

 e

1

ðde

 e

þ e

 de

Þþn  and n ds ¼ 0, for Gauss’ second fun-

damental form one easily ﬁnds

dn ds ¼ Lðdx

þ 2Mdx

þ Nðdx

¼ b

;

L ¼ðEG F

1=2

det

;

M ¼ðEG F

1=2

det

;

ðb

Þ¼



;

N ¼ðEG F

1=2

det

ð9:61Þ

with the abbreviations r

¼ o

=ox

, r

¼ or

=ox

. While the ﬁrst fundamental form depends

only on the metric on E, the second fundamental form depends also on the embedding of E in R

(on

the differential dn of the normal vector n on E in R

Any point r 2Emay be chosen as origin of R

, and the Cartesian base fa

; a

g may in

particular be chosen such that a

; a

span the tangent plane on E and a

¼ n. Then, in a

neighborhood of this point, with the just introduced notation of derivatives the surface E is

described as r

ðx

; x

Þ¼ðr

ðx

þ 2r

þ r

ðx

Þ=2 þ; x

¼ r

; x

¼ r

, where the

derivatives are taken at the origin. By a rotation of the ðx

; x

Þ-plane around n this expression

may be brought to the form r

ðx

; x

Þ¼ðk

ðx

þ k

ðx

Þ=2 þfrom which it is immedi-

ately seen that k

are the two principal curvatures in the two (orthogonal to each other) principal

curvature directions e

¼ a

and e

¼ a

, that is, the inverse values of the curvature radii of the

corresponding parabolic intersection lines of the planes spanned by e

and n with E. The total

Fig. 9.3 A smooth surface E

embedded in the Euclidean

space R

9.5 Sectional Curvature 323

curvature or Gaussian curvature is deﬁned as the product Kðx

; x

Þ¼k

. The signs of k

and

depend on the orientation of E (or n, determined by the choice of subscripts of e

and e

Their product K, however, is a true scalar. The special choice of coordinates implies r

; r

¼ 0 for i ¼ 1; 2 and r

¼ k

. Hence, LN  M

¼ K; EG F

¼ 1, and the canonical

fundamental forms are (compare (9.46))

¼ðdx

þðdx

; dn ds ¼ k

ðdx

þ k

ðdx

: ð 9:62Þ

Now, K has a geometric meaning of the embedding of E in R

which is independent of used

coordinates. On the other hand, g

and b

are tensors of type ð0; 2Þ in two dimensions, and hence

the quotient det b=det g is also independent of used coordinates. Hence,

K ¼

det b

det g

LN  M

EG F

ð9:63Þ

holds independently of chosen coordinates.

Let the frame fe

; e

; ng move on E. The corresponding derivatives of e

at ðx

; x

Þ may be re-

expanded into the frame there:

l¼1

þ b

n: ð9:64Þ

The ﬁrst term is an intrinsic relation on E and does not make use of the embedding in R

Identifying in view of the ﬁrst line of (9.59) e

with o=ox

, this term becomes a case of (7.41) and

recovers C

as the Christoffel symbols of the two-dimensional Riemannian manifold E, which

according to (9.23) are expressed in terms of derivatives of the metric tensor g. As regards the

second term, the general property e

 n ¼ 0 of the considered frame implies de

 n ¼e

 dn,

and scalar multiplication of (9.64) with n dx

, dx

and dx

arbitrary, and summation over the

two values of j and k yields b

¼ðoe

=ox

Þn dx

¼e

ðon=ox

Þdx

¼ds  dn,

which agrees with (9.61). Equation 9.64 is Gauss’ equation for the moving frame. For the change

of n, Weingarten’s equation

¼

j¼1

; g

¼ d

; ð9:65Þ

is obtained, where summation over l ¼ 1; 2 as tensor multiplication is understood and as usual

ðg

Þ is the inverse of ðg

Þ. First of all, n

¼ 1 implies n  dn ¼ 0, and hence a term proportional

to n is missing on the right hand side. Scalar multiplication of (9.65) with e

, the latter two

again arbitrary, and summation yields ðon=ox

Þe

¼ dn  ds ¼b

and hence

ðon=ox

Þe

¼b

. The ﬁnal result follows since g

¼ e

 e

implies

¼ 1.

The relations (9.64, 9.65) comprise 18 differential equations for the 9 functions e

; e

; n of

and x

, and hence for their solubility by smooth functions integrability conditions must be

imposed on their right hand sides. These are the 9 conditions

þ b



þ b



;

ð9:66Þ

In the present context, most important of the implications of a straightforward but lengthy

analysis (preferably in the above particular coordinates of R

) of these integrability conditions is

Gauss’ theorema egregium (exquisite theorem)

324 9 Riemannian Geometry

Kðx

Þ¼

1212

det g

; R

1212

122



121

j¼1

2j2

 C

2j1



ð9:67Þ

Gauss found it amazing since the two principal curvatures k

and k

clearly depend on ðb

Þand

hence on the second fundamental form, that is, on the embedding of E in R

while their product does

not. It is uniquely deﬁned by the metric ðg

Þof E and hence can be determined by measurements on

E alone without reference to the embedding in R

. For instance, on a cylinder one of the principal

curvatures is zero and the other is non-zero. On a plane both values are zero. The total curvature K is

zero in both cases, and in fact both manifolds per se are isometric and locally essentially equivalent,

their embedding in R

, however, is locally different.

Comparison of (9.67) with (7.48) shows, that R

1212

is the component of the curvature tensor,

which due to the general properties (9.34) in the case of a two-dimensional Riemannian geometry

is up to permutations of subscripts the only non-zero tensor component of the curvature tensor

ijkl

: for i ¼ j or k ¼ l it is zero, and the remaining components are equal up to a sign.

Returning to the general case, let M again be a Riemannian geometry of

dimension m, let u 2 M, and let X and Y span the two-dimensional subspace

E  T

ðMÞ. Choose an orthogonal frame fe

; ...; e

g at u for which e

; e

span E.

Consider the submanifold E of M formed by the points of all geodesics through u

and tangent to E. Then, E is given by the conditions

E : v

¼ 0; r ¼ 3; ...; m; ð 9:68Þ

for the normal coordinates v

at u. The submanifold E is a two-dimensional

Riemannian geometry with metric tensor (cf. (9.9))



ðv

; v

Þ¼g

ðv

; v

; 0; ...; 0Þ; 1 i; j 2; ð9:69Þ

inherited from the metric tensor g

of M, and v

; v

are normal coordinates at u in

E since the shortest path in M between two points of E, which is completely in E,is

a fortiori the shortest path in E between the points. Clearly, the Christoffel symbols

ijk

of E are









ijk

ðv

; v

Þð9:70Þ

again for 1 i; j; k 2. In particular, since v

are normal coordinates at u in both

manifolds,

ijk

ð0Þ¼C

ijk

ð0Þ¼0 at u. Hence,

1212

ð0Þ¼

122



121



122



121





1212

ð0Þ: ð9:71Þ

At u one has det



gð0Þ¼g

 g

¼ Gðe

; e

Þ, so that ﬁnally the

important result

Kðu; EÞ¼

Rðe

; e

Gðe

; e

¼



1212

det



KðuÞð9:72Þ

9.5 Sectional Curvature 325

follows. (Recall, that the value of Kðu; EÞ is independent of the tangent vectors

X; Y 2 T

ðMÞ used which span E.)

The sectional curvature Kðu; EÞ in a Riemannian geometry M is equal to the

total curvature of the surface E formed by all geodesics through u which are

tangent to E, with the inherited metric.

A Riemannian geometry M is called wandering at u,ifKðu; EÞ¼KðuÞ is

independent of E  T

ðMÞ. Since RðW; X; Y; ZÞ is uniquely determined by all

RðX; Y; X; YÞ for all linearly independent X; Y 2 T

ðMÞ, and likewise for G,

ijkl

ðuÞ¼Kð uÞ g

ðuÞg

ðuÞg

ðuÞg

ðuÞ



; iff M is wandering at u:

ð9:73Þ

M is called a constant curvature space, if it is wandering at every point and

KðuÞ¼K is independent of u.

In three dimensions, for every real value of K there is up to positioning exactly

one two-dimensional connected constant curvature space; for K [ 0 it is a sphere

(of radius 1=K), for K ¼ 0 it is a plane, and for K\0 it is called a pseudo-sphere

(obtained by rotating a tractrix around its asymptote; it is singular on its largest

circumference).

9.6 Gravitation

(For further studies [4] is recommended.)

Identical physical entities as atoms or molecules from which one can say that

they are positioned at ﬁxed mutual distance emit characteristic light with identical

frequency spectra. This allows for the deﬁnition of an absolute time scale (unit of

time). Phenomenologically there is no velocity of propagation of information

observed exceeding the velocity of light in vacuum, which is found to be the same

in all directions. Therefore the speed of light is assumed to be a universal constant.

Distances on the other hand of remote events can only be measured reliably by

propagating light signals between them. It is natural to deﬁne distances by the time

interval a light signal needs to propagate forth and back between the events. This is

why Minkowski’s metric

¼ g

¼ðdx

ðdx

; dx

¼ cdt; ð9:74Þ

where t is time, c is the vacuum speed of light, and x

; x

are taken to be

Cartesian spatial coordinates, is assumed to have physical reality.

Think of a clock ﬁxed with an isolated particle (for instance realized by the

phase of a vibration mode of a molecule). In a frame attached to the particle,

i¼1

ðdx

¼ 0 and hence ds

¼ðcdt

. An observer, who sees the particle move

326 9 Riemannian Geometry