Eschrig H. Topology and Geometry for Physics
Подождите немного. Документ загружается.

g
1
gg
1
2
, and consider the corresponding isotropy group at e 2 G. It is given as
fðg
1
; g
2
Þjg
1
eg
1
2
¼ eg implying g
1
¼ g
2
. Hence, the isotropy group ðG GÞ
e
is
the diagonal D ¼fðg
1
; g
1
Þjg
1
2 GgG. Moreover, G G acts transitively on
G, since for arbitrary g; g
0
2 G there is g
0
¼ g
0
gg
1
¼ðg
0
; gÞg. Hence, ðG
GÞ=D ! G : ðg
1
; g
2
ÞD 7!g
1
eg
1
2
is a diffeomorphism of manifolds. By choosing
ðg
1
2
; g
1
2
Þ2D for a representative of the coset ðg
1
; g
2
ÞD one finds ðg
1
g
1
2
; eÞ
which together with the coset is mapped to g
1
g
1
2
by the above diffeomorphism, so
that the diffeomorphism is also a homomorphism of groups and hence it is a Lie
group isomorphism, ðG GÞ=D G. Consequently, if the Lie group G and hence
also D is compact, G ðG GÞ=D itself can be provided with an invariant metric
and thus be made into a homogeneous Riemannian manifold.
Consider the Lie algebra g T
e
ðGÞ of the Lie group G and introduce on it the
symmetric 2-form
jðX; YÞ¼trðadðXÞadðYÞÞ; X; Y 2 g: ð9:18Þ
It is called the Killing form or Killing–Cartan form of g. Since the elements of
the Lie algebra g are left invariant vector fields on G,(9.18) is clearly an invariant
2-form:
jðX; YÞ¼jðl
e
g
X; l
e
g
YÞ for all g 2 G; ð9:19Þ
where l
e
g
is the left translation of tangent vectors from e to g in G like in Sect. 6.1.
Recall from that section, that after choosing a base fX
1
; ...; X
m
g in g, one gets
adðX
i
ÞX
j
¼½X
i
; X
j
¼
P
m
k¼1
c
k
ij
X
k
with the structure constants c
k
ij
of the Lie group
G. Thus, adðX
i
Þ
k
j
¼ c
k
ij
is cast into an ðm mÞ-matrix acting on the m-dimensional
vector space g ¼ span
R
fX
1
; ...; X
m
g, the composition of adðYÞ with adðXÞ
becomes the matrix multiplication and the trace becomes the matrix trace. From
the theory of Lie algebras [2] and citations therein it is known that the Killing form
j is non-degenerate, iff the Lie algebra g is semi-simple; it is negative definite, iff g
is moreover the Lie algebra of a compact Lie group G: Hence,
gðX; YÞ¼jðX; YÞð9:20Þ
is an invariant metric making a compact semi-simple Lie group into a homoge-
neous Riemannian manifold, and it is an invariant indefinite metric making a
non-compact semi-simple Lie group into a generalized homogeneous Riemannian
manifold.
In the above considered simple case G ¼ OðnÞ, the Lie algebra is g R
n1
, and
after introducing a standard orthonormal base in R
n1
, gðX
i
; X
j
Þ¼g
ij
becomes the
unit matrix, related to standard orthogonal local coordinates on the sphere S
n1
.
In physics, a closed finite piece of a Riemannian manifold with fixed time-
independent distances between all of its points is called a rigid body. The pecu-
liarity of a homogeneous manifold is that a piece of it as a rigid body can move
through it without deformation. For that reason, after Riemann’s habilitation talk
9.2 Homogeneous Manifolds 307
where he introduced his revolutionary new concept of geometry, many scholars
including Helmholtz thought that physical relevance should be restricted to
homogeneous manifolds, because the free motion of rigid bodies in space was still
a dogma based on Kant’s absolute space and time. At least after Einstein’s theory
of relativity it is known that rigid bodies are an abstraction from the real world,
only possible in the limit of infinite velocity of light. Nevertheless, as this limit is
often a very good approximation, homogeneous manifolds may continue to have
relevance in kinematics and classical physics. Besides, Lagrangian Grassmannians
are important homogeneous manifolds forming subspaces of the phase space of
classical mechanics.
9.3 Riemannian Connection
Further on, M is a generalized Riemannian manifold with the metric form g. Like
any tensor field, g can be considered as a section in a tensor bundle over M which
is associated with the frame bundle ðLðMÞ; M; p; Glðm; RÞÞ as its principal fiber
bundle. In Sect. 7.7, linear connections on M were introduced as connections on
LðMÞ, and covariant derivatives r
X
t of tensor fields t in the direction of the
tangent vector X as well as covariant differentials rt were associated with linear
connections. A linear connection C on M is called a metric connection,ifrg ¼ 0
on M, a metric connection is called a Riemannian connection,orLevi–Civita
connection, if it is torsion free, T ¼ 0 on M. This is subject of the Fundamental
Theorem of Riemannian Geometry:
Every generalized Riemannian manifold allows for exactly one Riemannian
connection. It is defined by the following expression for r
X
Y valid for every
X; Y; Z 2 g:
2gðr
X
Y; ZÞ¼XgðY; ZÞþYgðX; ZÞZgðX; YÞ
gðX; ½Y; ZÞ gðY; ½X; ZÞþ gðZ; ½ X; YÞ; ð9:21Þ
where the first line on the right hand side is understood according to (7.26).
A Riemannian connection is said to define a pseudo-Riemannian geometry on
a generalized Riemannian manifold with indefinite metric tensor, it is said to
define a Riemannian geometry on a Riemannian manifold. A metric tensor
defines uniquely not only a (possibly indefinite) metric on M, but also a (pseudo-)
Riemannian geometry. A tensor bundle or more generally any vector bundle
associated with LðMÞ with a Riemannian connection is called a Riemannian
vector bundle and g is called a Riemannian structure on it.
Put in local coordinates X ¼ o=ox
i
; Y ¼ o=ox
j
and Z ¼ o=ox
k
into (9.21). From
(3.19) it is immediately seen that the second line of (9.21) vanishes in this case.
Recall gðo=ox
i
; o=ox
j
Þ¼g
ij
and, from (7.42), r
o=ox
i
ðo=ox
j
Þ¼
P
l
C
l
ij
ðo=ox
l
Þ. One
readily obtains
308 9 Riemannian Geometry

X
l
g
lk
C
l
ij
¼
1
2
og
jk
ox
i
þ
og
ik
ox
j
og
ij
ox
k
¼ C
ikj
: ð9:22Þ
The last expression defines new Christoffel symbols for the Riemannian
connection. For historical reasons they are also called Christoffel symbols of the
first kind while the general Christoffel symbols introduced in Sect. 7.9 are called
Christoffel symbols of the second kind. (Recall that Christoffel symbols are not
tensors.) For reference, some properties of Christoffel symbols valid for
Riemannian connections are given which are obvious from (9.22):
C
k
ij
¼
1
2
g
kl
og
il
ox
j
þ
og
jl
ox
i
og
ij
ox
l
¼ C
k
ji
; ð9:23Þ
C
ikj
¼ C
jki
;
og
ij
ox
k
¼ C
ijk
þ C
jik
: ð9:24Þ
Proof of the Fundamental Theorem Let a Riemannian connection be given and let
r be the corresponding covariant differential. Then, rg ¼ 0 and hT; X ^
Yi¼r
X
Y r
Y
X ½X; Y¼0 (see (7.31)). From (7.27), 0 ¼ðrgÞðY; Z; XÞ¼
r
X
gðY; ZÞgðr
X
Y; ZÞgðY; r
X
ZÞ¼XgðY; ZÞgðr
X
Y; ZÞgðY; r
Z
XÞg
ðY; ½X; ZÞ, since g is bilinear and gðY; ZÞ is a real function (see (7.26)). Likewise,
0 ¼r
Y
gðX; ZÞgðr
Y
X; ZÞgðX; r
Y
ZÞ¼YgðX; ZÞgðr
X
Y; ZÞgðZ; ½Y; XÞ
gðX;r
Y
ZÞ and 0 ¼r
Z
gðX;YÞgðr
Z
X;YÞgðX;r
Z
YÞ¼ZgðX;YÞgðr
Z
X;YÞ
gðX;r
Y
ZÞgðX;½Z;YÞ. Adding the first two relations and subtracting the last one
yields (9.21).
Conversely, assume that (9.21) is valid. Since g is non-degenerate, (9.21)
defines the action of r
X
on tangent vector fields Y uniquely, its action on functions
is understood according to (7.26) by definition. Hence, according to Sect. 7.7
the action of r
X
on tensor fields is uniquely defined, if it is a derivative. Due to
multi-linearity of the right hand side of (9.21), (7.18) is readily fulfilled, and the
validity of (7.19) is easily checked. Hence, (9.21) defines a covariant derivative
with Christoffel symbols (9.23) for which the demanded transformation properties
(7.38) may straightforwardly calculated from the latter expression. This shows that
(9.21) defines uniquely a linear connection on M. With (9.24) and (7.43), rg ¼ 0
is straightforwardly calculated, and hence C is a metric connection. It is torsion
free which follows most easily from (7.47) and (9.23). h
The reader should perform the straightforward calculations of this proof as an
exercise.
Useful relations are obtained from
g
ij
C
k
ij
¼
1
2
g
ij
g
kl
og
il
ox
j
þ
og
jl
ox
i
og
ij
ox
l
¼ g
il
g
kj
og
ij
ox
l
1
2
g
kl
g
ij
og
ij
ox
l
:
9.3 Riemannian Connection 309

From g
kj
g
ij
¼ d
k
i
it follows that g
kj
og
ij
=ox
l
¼g
ij
og
kj
=ox
l
, and hence the first term
of the displayed result is og
kl
=ox
l
. Since ðg
ij
Þ is the matrix inverse to ðg
ij
Þ the
element g
ij
is the minor of g
ij
divided by det g,ordet gg
ij
¼ o det g=og
ij
and hence
o det g
ox
l
¼
o det g
og
ij
og
ij
ox
l
¼ det gg
ij
og
ij
ox
l
¼det gg
ij
og
ij
ox
l
: ð9:25Þ
The last equality is just a special case of the preceding consideration. Now, one
has
g
ij
C
k
ij
¼
og
kl
ox
l
1
2
g
kl
det g
o det g
ox
l
¼
1
ffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
o
ffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
g
kl
ox
l
: ð9:26Þ
On the other hand, rg ¼ 0 implies g
kl
;l
¼ 0, and with (7.44, 7.45) this means
og
kl
=ox
l
¼ g
ml
C
k
ml
þ g
km
C
l
ml
, which combines with (9.26)to
C
i
ji
¼
1
ffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
o
ffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
ox
j
: ð9:27Þ
The latter result yields for the divergence C
1;1
rX of a vector field X
X
i
;i
¼
oX
i
ox
i
þ C
i
ji
X
j
¼
1
ffiffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
oð
ffiffiffiffiffiffiffiffiffiffiffiffi
jdet gj
p
X
i
Þ
ox
i
: ð9:28Þ
A similar expression is obtained for the divergence t
ij
; j
of an alternating tensor t.
Let local coordinates be given in LðMÞ as before (7.23), and let it be provided
with a Riemannian connection with connection form x. Then, the first structure
equation (7.23) for vanishing torsion reads (as previously, the index a of a
coordinate neighborhood is only occassionally used for the sake of clarity at local
forms and is dropped here)
dh
i
X
j
h
j
^ x
i
j
¼ 0: ð9:29Þ
In view of (7.43), the condition for x to be a metric connection reads 0 ¼
rg ¼ðog
ij
=ox
k
C
l
ki
g
lj
C
l
kj
g
il
Þdx
i
dx
j
dx
k
¼ðdg
ij
g
lj
x
l
i
g
il
x
l
j
Þdx
i
dx
j
,
where in the last equality the definition of the Christoffel symbols by the local
connection form given on p. 241 was used. Hence, this condition reads
dg
ij
g
lj
x
l
i
g
il
x
l
j
¼ 0; ð9:30Þ
where dg
ij
is the ordinary differential of the component of the symmetric 2-form g.
These last two relations yield an equivalent formulation of the Fundamental
Theorem of Riemannian Geometry:
Given a generalized Riemannian manifold M with metric form g and given m
linearly independent 1-forms h
i
; i ¼ 1; ...; m on every coordinate neighborhood U
310 9 Riemannian Geometry
of M, there exists a unique set of m
2
1-forms x
i
j
solving the equations (9.29, 9.30)
and forming local connection forms of a Riemannian connection. The metric form
may then be expressed as g
kl
h
k
h
l
:
Use coordinate lines according to the integral curves of m standard horizontal
vector fields X
i
; hh
k
; X
i
i¼d
k
i
(p. 234). Then, g
ij
¼ gðX
i
; X
j
Þ¼g
kl
hh
k
; X
i
ihh
l
; X
j
i.
In the case of a Riemannian manifold (that is with a positive definite metric form)
one may choose linearly independent standard horizontal vector fields for which
g
ij
¼ d
ij
and hence ds
2
¼
P
i
ðh
i
Þ
2
. Then, (9.30) yields a skew-symmetric local
connection form: x
i
j
þ x
j
i
¼ 0.
Since g
ij
ðxÞ is a smooth function, the exterior derivative of its differential
vanishes: d ^ dg
ij
¼ 0. The exterior derivative of (9.30) yields 0 ¼ g
kj
x
k
l
^
x
l
i
þ g
lk
x
k
j
^ x
l
i
þ g
lj
dx
l
i
þ g
kl
x
k
i
^ x
l
j
þ g
ik
x
k
l
^ x
l
j
þ g
il
dx
l
j
. The second and the
fourth terms cancel, and, after some renaming of summation indices, ðx
l
k
^ x
k
i
þ
dx
l
i
Þg
lj
þ g
il
ðx
l
k
^ x
k
j
þ dx
l
j
Þ¼0 results. According to (7.23), the parentheses of
the last relation contain the components of the curvature form X ¼ dx þ x ^ x,
so that this relation reads
X
l
i
g
lj
þ g
il
X
l
j
¼ 0: ð9:31Þ
X
ij
¼ X
l
i
g
lj
of a Riemannian connection (with possibly indefinite metric) is skew-
symmetric.
Expressing (7.30) in local coordinates results in (exercise, see also the text of
the next paragraph)
X
i
j
¼
X
k\l
R
i
jkl
dx
k
^ dx
l
; ð9:32Þ
where the curvature tensor R is given by (7.49). The curvature tensor field of a
generalized Riemannian manifold,
R
ijkl
¼ g
im
R
m
jkl
; ð9:33Þ
has the following properties:
R
ijkl
¼R
jikl
¼R
ijlk
;
R
ijkl
þ R
iklj
þ R
iljk
¼ 0;
R
ijkl
¼ R
klij
:
ð9:34Þ
The first line follows directly from (9.31, 9.32). To obtain the second line, first
realize that (9.29) must hold locally for any linear independent system of 1-forms
h
i
. Putting locally h
i
¼ dx
i
yields 0 ¼
P
j
x
i
j
^ dx
j
. take the exterior derivative of
this relation and use it again to get 0 ¼
P
j
dx
i
j
^ dx
j
¼
P
j
ðX
i
j
P
k
x
i
k
^ x
k
j
Þ^
dx
j
¼
P
j
X
i
j
^ dx
j
. Insert (9.32) and obtain
P
j\k\l
R
i
jkl
dx
j
^ dx
k
^ dx
l
¼ 0 from
which the second line follows. Interchanging in the second line i with j, subtracting
9.3 Riemannian Connection 311

the result from the second line and observing the first line yields 2R
ijkl
þ
R
iklj
þ R
ljik
þ R
iljk
þ R
jkil
¼ 0. Interchanging here ij with kl, subtracting and
observing again the first line of (9.34) yields the third one.
Finally, exterior differentiation of X ¼ dx þx ^ x yields the Bianchi identi-
ties in the form dX ¼ dx ^ x x ^dx ¼ X ^ x x ^X. This relation, which is
still a relation of forms on the frame bundle, in the notation of (7.30) paired with
tangent vectors X
on LðMÞ, may be pulled back from the canonical section to the
base manifold M as the same relation for the corresponding local forms on a
trivializing coordinate neighborhood in M, which are paired with tangent vectors
X on M as hX
a
; ðo=ox
k
Þ^ðo=ox
l
Þi ¼ R
i
jkl
dx
j
ðo=ox
i
Þ or X
i
aj
¼
P
R
i
jkl
dx
k
^ dx
l
(compare the text before (7.5) and before (7.14) as well as (7.46) and (9.32)).
Insert this expression together with x
i
aj
from p. 241 into the relation dX
i
aj
¼
x
i
an
^ X
n
aj
þ X
i
an
^ x
n
aj
and obtain
X
oR
i
jkl
ox
m
dx
m
^ dx
k
^ dx
l
¼
X
C
i
mn
R
n
jkl
þ C
n
mj
R
i
nkl
dx
m
^ dx
k
^ dx
l
:
Complete the left hand side to a covariant derivative according to (7.43) and get
X
R
i
jkl;m
dx
m
^ dx
k
^ dx
l
¼
X
C
n
mk
R
i
jnl
þ C
n
ml
R
i
jkn
dx
m
^ dx
k
^ dx
l
:
Now, this right hand side vanishes in the torsion free case, because according to
(7.47) in this case the Christoffel symbols are symmetric in the lower indices.
Hence, also the left hand side vanishes, which means that the corresponding
alternating combination of R
i
jkl;m
in the last three subscripts must vanish. This is the
sum with cyclic permutation minus the sum with anti-cyclic permutation of these
subscripts. In view of the alternating dependence of R on its last two subscripts the
six items can be combined into three. Thus,
R
ijkl;m
þ R
ijlm;k
þ R
ijmk;l
¼ 0 ð9:35Þ
expresses the Bianchi identities for a Riemannian connection.
9.4 Geodesic Normal Coordinates
In this section, the linear connection on M is specialized step by step.
First a general manifold M with a linear connection is considered, that is, the
frame bundle LðMÞ with a linear connection C. In a coordinate neighborhood
U
a
M, the system of ordinary differential equations (7.51),
d
2
x
i
dt
2
þ
X
jk
C
i
jk
dx
j
dt
dx
k
dt
¼ 0; i ¼ 1; ...; m; ð9:36Þ
312 9 Riemannian Geometry

has the geodesics as solutions, which are the curves in M whose tangent vector is
transported parallel to itself along the curve. As is well known from standard
analysis, given initial conditions
x
i
ð0Þ¼u
i
;
dx
i
dt
0
¼ v
i
; ð9:37Þ
there are a neighborhood U U
a
and two positive real numbers r; d, so that for all
ðu
i
Þ2U ¼ u
a
ðUÞ and ðv
i
Þ¼v 2 R
m
; jvj\r the system (7.51) has a unique
solution
x
i
¼ y
i
ðt; u
k
; v
k
Þ for jtj\d; ð9:38Þ
where y
i
depends smoothly on t; u
k
; v
k
. It may be thought of as a motion in time t
through M passing at t ¼ 0 through ðu
k
Þ with velocity vector ðv
k
Þ. Rescaling the
time by a factor c is equivalent to rescaling the velocity with 1=c:
y
i
ðct; u
k
; v
k
=cÞ¼y
i
ðt; u
k
; v
k
Þ or y
i
ðct; u
k
; v
k
Þ¼y
i
ðt; u
k
; cv
k
Þ: ð9:39Þ
In these relations, the left hand side is defined where the right hand side was
defined in (9.38). Take jcj\d and fix ðu
k
Þ2U. Then, with the first initial con-
dition (9.37), the relation
x
i
¼ y
i
ð1; u
k
; v
k
Þ with u
i
¼ y
i
ð0; u
k
; v
k
Þ¼y
i
ð1; u
k
; 0Þ¼u
i
ð9:40Þ
provides a mapping ðv
k
Þ7!ðx
i
Þ from a neighborhood of the origin of T
u
ðMÞR
m
onto a neighborhood of u 2 M with the origin of T
u
ðMÞ mapped to u. Indeed, now
with the second initial condition (9.37),
oy
i
ð1; u
k
; v
k
Þ
ov
v¼0
v ¼
oy
i
ð1; u
k
; tv
k
Þ
ot
t¼0
¼
oy
i
ðt; u
k
; v
k
Þ
ot
t¼0
¼ v
i
and hence oy
i
ð1; u
k
; v
k
Þ=ov
j
v¼0
¼ d
i
j
so that the mapping is regular at v ¼ 0 and
provides a bijection of some neighborhood of v ¼ 0 onto a neighborhood of
u 2 M. This latter neighborhood is a coordinate neighborhood of M with coordi-
nates v
i
whose transition to the original coordinates x
i
is defined by the first
relation (9.40). The coordinates v
i
are called geodesic normal coordinates at u or
in short normal coordinates. Of course, they are determined up to the choice of a
base in T
u
ðMÞ, that is up to a non-degenerate linear transformation. (So far, M is a
linear connection space, a metric in M and angles in T
u
ðMÞ were not yet intro-
duced.) For every u 2 M and every fixing of a base in T
u
ðMÞ there is a neigh-
borhood UðuÞ and a local coordinate system in UðuÞ of geodesic normal
coordinates at u; it is called a normal coordinate neighborhood of u.
Choose a coordinate neighborhood U
a
M (with respect to coordinates x
i
), a
point u 2 U
a
and a base fX
iu
ji ¼ 1; ...; mgin T
u
ðMÞ, and consider a tangent vector
X
u
¼
P
i
v
i
X
iu
. The points with geodesic normal coordinates ðv
i
¼ t
v
i
Þ form a
9.4 Geodesic Normal Coordinates 313
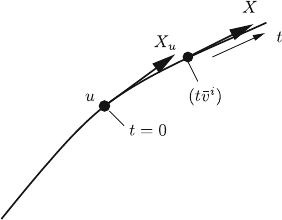
geodesic through the point u 2 M (at t ¼ 0) which has X
u
as its tangent vector at u.
If this tangent vector is parallel transported along the geodesic, it remains tangent to
it in all points of the geodesic (Fig. 9.1). From the above analysis it is clear that
given a point u
0
2 UðuÞ with normal coordinates v
i
(with respect to u), the tangent
vector X
u
of a geodesic from u to u
0
is uniquely defined up to a scaling factor with an
inverse scaling of the curve parameter t of the geodesic. Such a rescaling does of
course not change the geodesic curve itself, it changes only its parametrization.
In a normal coordinate neighborhood UðuÞ of u 2 M, there is for every point
u
0
2 UðuÞ a uniquely defined geodesic curve connecting u and u
0
.
For small enough q [ 0, there is a q-ball neighborhood
U
q
ðuÞ¼ x
X
m
i¼1
ðv
i
ðxÞÞ
2
\q
2
()
; U
q
ðuÞ¼ x
X
m
i¼1
ðv
i
ðxÞÞ
2
\q
2
()
ð9:41Þ
of u contained in the normal coordinate neighborhood UðuÞ (U
q
ðuÞ¼u
a
ðU
q
ðuÞÞ).
Moreover, if B
d
ð0Þ is the open ball of radius d centered at the origin of the
Euclidean space R
m
, then there is d [ 0 so that through every point u
0
2 U
q
ðuÞ and
for every v 2 B
d
ð0Þ there is a unique geodesic through u
0
with tangent vector v at u
0
and given by x
i
¼ y
i
ðt; u
0
k
; v
k
Þ; jtj\2. In summary, there is a mapping
w : U
q
ðuÞB
d
ð0Þ!U
q
ðuÞU
a
: ðu
0
k
; vÞ7!wðu
0
k
; vÞ¼ðu
0
k
; y
k
ð1; u
0
k
; v
k
ÞÞ:
ð9:42Þ
For every u 2 U
a
there are such positive numbers q and d (depending on u). Of
basic importance for the following is the statement visualized in Fig. 9.2:
For any point u in a linear connection manifold M there exists a neighborhood
W of u such that every point u
0
2 W has a normal coordinate neighborhood Uðu
0
Þ
that contains W.
Proof By the analysis after (9.39), the Jacobian of the mapping w is ½oðu
0
k
; y
k
Þ=
oðu
0
k
; v
k
Þ
ðu;0Þ
¼ 1. Hence, the differential w
ðu;0Þ
is a linear isomorphism, and from
the inverse function theorem (Sect. 3.5, case 3) it follows that there is a neighbor-
hood V of ðu; 0Þ2U
q
ðuÞB
d
ð0Þ and a positive number \d so that the restriction
Fig. 9.1 A geodesic through
the point u with the
corresponding geodesic
normal coordinates
314 9 Riemannian Geometry
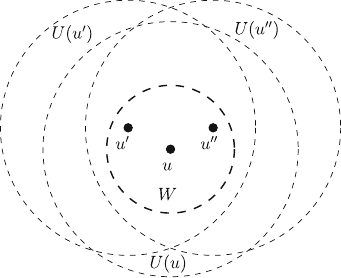
wj
V
:V ! U
ðuÞU
ðuÞ is a diffeomorphism. For every point u
0
2 U
ðuÞ take the
set of vectors B
u
0
¼fv 2 B
ð0Þjðu
0
; vÞ2Vg. Then, the set of points x 2 U
a
with
a-coordinates x
i
¼ y
i
ð1; u
0
k
; v
k
Þ; v 2 B
u
0
is contained in a normal coordinate
neighborhood Uðu
0
Þ of u
0
and is diffeomorphic to U
ðuÞ¼W: h
An immediate consequence is that every pair of points of W can be connected
by a geodesic.
Now, let the linear connection space W additionally be torsion-free. The normal
coordinates along a geodesic through a given point u may be chosen v
i
¼ t
v
i
,
hence d
2
v
i
=dt
2
¼ 0, with t ¼ 0 at u, and for instance unit vectors
v, and the system
(9.36)atu, expressed with the normal coordinates v
i
instead of the x
i
, reads
P
jk
C
i
jk
ð0Þ
v
j
v
k
¼ 0, where now the Christoffel symbols C
i
jk
ðv
l
Þ refer to the normal
coordinates at u. Since in the torsion-free case these symbols are symmetric in the
lower indices in any coordinate system, it follows that C
i
jk
ð0Þ¼0 for all
i; j; k ¼ 1; ...; m.
At any point u of a torsion-free linear connection manifold M, by choosing
geodesic normal coordinates at u the Christoffel symbols C
i
jk
ð0Þ at u are made
vanish.
This is again an indication that the Christoffel symbols do not form a tensor, for
a tensor vanishing in some coordinate system would vanish in any coordinate
system.
Another remarkable property of torsion-free linear connection manifolds is that
the local connection form of a torsion-free linear connection manifold M is
uniquely defined by the curvature tensor.
Proof Let u 2 M be any point and let UðuÞ be a normal coordinate neighborhood
of u. Fix a frame ðu; X
1
; ...; X
m
Þ at u and choose corresponding geodesic normal
coordinates in the following way:
P
i
v
i
X
i
;
P
i
ð
v
i
Þ
2
¼ 1; is a tangent vector at u in
any direction given by the components
v
i
with respect to the fixed frame; ðv
i
Þ¼
ðt
v
i
Þ are geodesic normal coordinates in UðuÞ on geodesics having the tangent
Fig. 9.2 See statement on
the previous page
9.4 Geodesic Normal Coordinates 315

vector
P
i
v
i
X
i
at u. Build a frame field in UðuÞ by transporting the chosen frame at
u parallel (horizontally in LðMÞ) along geodesics. Tangent vectors to geodesics,
expressed in the polar coordinates
v
i
; t;
P
i
ðv
i
Þ
2
¼ 1 are o=ot and have constant
components
v
i
with respect to this frame field along geodesics through u. Since the
frame field is spanned by horizontal vectors, m linearly independent vector fields
X
j
with constant components
v
i
j
extend to standard horizontal vector fields Bð
v
j
Þ on
LðMÞ (compare (7.7)). Hence, according to (7.24), the canonical 1-form h and the
connection 1-form x are given as h
i
¼
v
i
dt þ
h
i
; x
i
j
¼
x
i
j
, where
h
i
and
x
i
j
depend
on the
v
i
and on t but do not contain dt (annihilate tangent vectors to geodesics
v ¼ const.). Moreover, since at t ¼ 0 a tangent vector in any direction is
proportional to dt (away from t ¼ 0 this holds only for vectors tangent to the
constructed geodesics through u),
x
i
j
j
t¼0
¼ 0 and
h
i
j
t¼0
¼ 0:
In view of the vanishing torsion, the structure equations (7.23) read
dh
i
þ
X
j
x
i
j
^ h
i
¼ 0; dx
i
j
þ
X
k
x
i
k
^ x
k
j
¼ X
i
j
: ð9:43Þ
Since each component X
i
j
of the tensorial curvature form X is a horizontal 2-form,
it can be expressed as X
i
j
¼
P
k\l
R
i
jkl
h
k
^ h
l
. In fact,
R
i
jkl
is the (bijective) u-trans-
formation of the curvature tensor R
i
jkl
¼ u
i
p
R
p
qrs
ðu
1
Þ
q
j
ðu
1
Þ
r
k
ðu
1
Þ
s
l
in the meaning of
(7.30) and (7.6); the u-transformation is not to be confused with the point u above.
The components of both tensors R and
R are functions of the
v
i
and of t. Comparing in
the equations (9.43) of forms only the terms proportional to dt yields
d
v
i
o
h
i
ot
þ
X
j
x
i
j
v
j
!
^ dt ¼ 0;
o
x
i
j
ot
X
kl
R
i
jkl
v
k
h
l
!
^ dt ¼ 0: ð9:44Þ
(Note that d
h
i
¼ dt ^ðo
h
i
=otÞþ¼ðo
h
i
=otÞ^dt þ:) Hence, the expres-
sions in parentheses must vanish. A further differentiation of the first expression
with respect to t (t and
v
i
are independent) and then insertion of the second results in
o
2
h
i
ot
2
X
jkl
R
i
jkl
v
j
v
k
h
l
¼ 0: ð9:45Þ
Given R
i
jkl
and hence
R
i
jkl
, this last equation is in fact an ordinary differential
equation for
h
i
, which with the initial conditions h
i
j
t¼0
¼ 0 and ðo
h
i
=otÞ
t¼0
¼
d
v
i
þ
P
j
v
j
x
i
j
j
t¼0
¼ d
v
i
has a unique solution
h
i
ð
v
k
; tÞ¼
P
j
h
i
j
ð
v
k
; tÞd
v
j
þ
h
i
t
ð
v
k
; tÞdt. (Recall that the components
h
i
are 1-forms, (9.45) is an equation of
forms and contains an equation for every
h
i
j
and every
h
i
t
:)
Finally, take any point in UðuÞ with coordinates ðv
i
Þ¼ðt
v
i
Þ. For every fixed
l ¼ 1; ...; m there is a (non-unique) regular linear transformation w with
v
j
¼
P
k
w
j
k
d
k
l
. Inserting this into the first equation (9.44) yields
316 9 Riemannian Geometry
