Eschrig H. Topology and Geometry for Physics

Подождите немного. Документ загружается.

with velocity v relative to himself, observes in the same interval ds (which is an

invariant and hence the same in all reference systems) the particle run a distance

ðdx

¼ðvdtÞ

. Hence, ðcdt

¼ ds

¼ðcdtÞ

ðvdtÞ

¼ dt

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 



: ð9:75Þ

The time interval dt

is the proper time interval experienced by the particle.

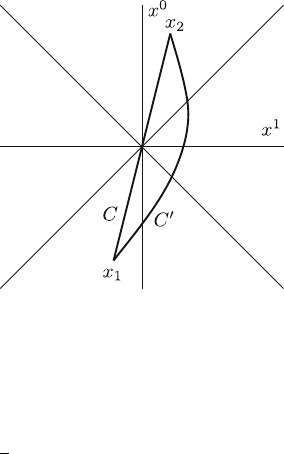
Consider an observer moving with constant speed on a straight world line C

(Fig. 9.4) and observing a particle departing from his own position x

and

returning to him at position x

. Since the particle moves relative to the observer, its

proper time t

stays all the way behind that of the observer, t. (In Fig. 9.4 an

inertial reference system is used which moves relative to both observer and par-

ticle. Of course both must have velocities not exceeding c, indicated by the two

lines x

¼ct in the ﬁgure.) Hence,

 t

ds [

ds ¼ t

 t

;

and clearly the straight world line has the maximum length of all world lines

between two given world points. (The situation is asymmetric between C and C

because in vacuum a set of reference systems which move relative to each other at

most with constant speed is distinguished as inertial systems.)

A massive particle propagates between world points (events) x

and x

on a

world line C which is determined by the principle of least action. If nothing is

present besides the particle, the only invariant action that can be formed is

S ¼mc

ds ¼

Ldt; ð9:76Þ

Fig. 9.4 World lines of

observer, C, and a particle, C

9.6 Gravitation 327

where the prefactor is convention and sets a mass or energy scale while the minus

sign is needed because in Minkowski’s metric, as just shown, the integral has a

maximum but no minimum. It yields the Lagrange function L ¼mc

ð1 ðv=cÞ

1=2

, where v is the velocity of the particle. In general geometric terms

this action means that the world line of the particle is a geodesic in the Minkowski

space, which is a straight line.

However, if a force acts on the particle, its motion is accelerated, and it turns

out that, if the force is that of a gravitational ﬁeld, all accelerations of all particles

passing a region where the ﬁeld has a certain value (measured statically by means

of a spring-balance) are the same independent of the particle mass. Exactly the

same way force-free particle motions are seen by an accelerated observer, that is, if

the particle coordinates are described with respect to an accelerated frame.

Because these two situations are indistinguishable and (9.74) is invariant under

mere changes of the coordinates, the same action (9.76) must describe the motion

of a particle under the action of a gravitational ﬁeld, while the metric tensor g

now may be much more general than in the case of use of mere general coordinates

in the above discused case of absence of gravitation. Hence, the world line of a

particle in a gravitational ﬁeld is still a geodesic, but now in a more general metric.

If one takes the geodesic arc length s as curve parameter, the equation of motion is

lm¼0

¼ 0; ð9:77Þ

with the Christoffel symbols C

of the Riemannian connection of the metric

tensor g now describing the action of the gravitational ﬁeld. The Christoffel

symbols are obtained from derivatives of the metric tensor with respect to the

coordinates, hence the metric tensor itself may be viewed as forming gravitational

potentials.

Since coordinates are now arbitrary and cannot have any more an immediate

physical meaning, their relation to time intervals and distances in ordinary space

must be analyzed. In this section, systematically Latin tensor indices run from 1 to

3, Greece indices run from 0 to 3, and t means the physical time, that is the proper

time of a material entity. Although a consequent covariant formulation of physical

laws as used in the theory of gravitation would tolerate the use of completely

arbitrary (smooth) coordinate systems, every point of physical space time is the

apex of a cone of future and of a cone of past, and the convention is reasonable to

use only coordinate systems where the coordinate line for x

runs from the past to

the future while the coordinate lines of x

are outside of the cones. Such coordi-

nates may be realized by material constructions (sample holders and clocks). If in

such a case dx

¼ 0, then ds

¼ g

ðdx

¼ðcdtÞ

, and

dt ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðxÞ

; t ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðxÞ

; g

ðxÞ[ 0; ð9:78Þ

328 9 Riemannian Geometry

describes the proper time of a world line x

ðsÞ. To ﬁnd an expression for spatial

distances, consider two neighboring world lines C and C

with their proper times t

and t

. Send a light signal from C to C

which arrives at C

at world point x

and is

reﬂected back to C. It departs from C at world point x

þ dx

and returns to C at

þ dx

. For the propagation forth and back (a ¼ 1; 2) one has

0 ¼ g

¼ g

ðdx

þ 2g

þ g

Assume the two world lines kept at constant spatial distance, dx

¼ dx

Then,

¼



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðg

 g



with the upper sign for a ¼ 1 and the lower sign for a ¼ 2 yield the proper time

interval on world line C from departure to return of the light signal as

dt ¼

ﬃﬃﬃﬃﬃﬃ

ðdx

 dx

Þ¼

ﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðg

 g

Þdx

This time is apparently two times the spatial distance between the world lines

divided by c, hence the square of the distance is



;



 g

;



¼g

; ð9:79Þ

with the metric tensor



of the spatial submanifold in a coordinate neighborhood

of materializable coordinates x

of space–time given by x

¼ const. The last

relation, in which as usual ðg

Þ is the inverse of ðg

Þ and likewise for ð



Þ,isa

simple exercise.

For physical reasons, since it describes spatial distances,



must be a positive

deﬁnite metric. This implies for the submatrices



[ 0; det





[ 0; det



g [ 0: ð9:80Þ

The last equations (9.78) and (9.79) then require

[ 0; det



\0; det

[ 0; det g\0:

ð9:81Þ

(Caution: Some authors of physics textbooks, including [4], use a convention

¼g

, then only \ signs appear in (9.81), and the second and third

relations (9.79) have reversed signs.) These relations must be fulﬁlled in any

coordinate system realized by matter constructions.

9.6 Gravitation 329

As a simple example, consider an observer at rest and use cylinder coordinates

ðx

; r

; u

; z

Þ,

¼ðdx

ðdr

 r

ðdu

ðdz

Let the observer rotate around the z

-axis with angular velocity x. He now makes

observations with respect to coordinates x

¼ x

; r ¼ r

; u ¼ u

ðx=cÞx

;

z ¼ z

, and

¼ 1 



ðdx

 2

dudx

ðdrÞ

 r

ðduÞ

ðdzÞ

For r [ c=x one would have g

\ 0 and hence outside of this radius the

considered rotating coordinate systems would not be materializable. Matter at

radius r \ c=x, seen at rest by the rotating observer, ‘in truth’ moves with velocity

v ¼ xr in the primed coordinates. The proper time t of the rotating matter is

related to the time t

of an observer at rest as

dt ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 

: ð9:82Þ

Compared to a time interval Dt

¼ Dx

=c ¼ Dx

=c, its proper time interval is

DtðrÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

Dtð0Þ . Light emitted from this matter

at r by atomic vibrations is observed at r ¼ 0 by the observer who is measuring

with his atomic clocks at rest ticking with frequency mðr ¼ 0Þ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

mðrÞ. Since the clocks of the observer tick at lower frequency, he

registers the incident light coming from r blue shifted and approaching inﬁnite

frequency for r ! c=x from below.

Consider the observed circumference of a circle of radius r:

L ¼

dl ¼

ﬃﬃﬃﬃﬃﬃﬃﬃ



du ¼ 2p

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

 g

2pr

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

: ð9:83Þ

The observed radius would be unchanged: R ¼

ﬃﬃﬃﬃﬃﬃ



dr ¼

dr ¼ r. The

observed ratio L=R approaches the familiar value 2p only for r ! 0 and is

otherwise larger than 2p, diverging for r ¼ c=x. The reason is the following.

Assume, in the primed system at rest an observer calibrates a measuring rod to

have length l

¼ r

=n ¼ r=n; n  1, and lays it down tangent to the circle with

radius r centered at r

¼ r ¼ 0. Its ends seen from the origin form an angle

¼ l

=r ¼ 1=n. The rotating observer sees the rod move with velocity v ¼ xr

(against the rotation direction), and hence sees it Lorentz contracted to length

l ¼ l

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

. Its ends seen from him at the origin form an angle

du ¼ du

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

=n. This comes about by synchroniza-

tion of clocks at both ends of the rod in the rotating system. A by a factor

330 9 Riemannian Geometry

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  x

larger number of rods is needed to cover the full angle of 2p, or,

alternatively expressed, the seen angle summed up of rods ﬁlling one circumfer-

ence is smaller than 2p.Atr ¼ c=x the rods would be seen shrunk to zero. The

observed 2-space perpendicular to z is not Euclidean any more, it has got a neg-

ative curvature. (On a sphere having positive curvature, obviously L=R \ 2p,if

the radius is measured from a pole along a great circle.)

The proper time t of rotating matter (including electromagnetic matter as light)

so that it is at rest in the rotating system is related to the time t

of the observer at

rest at r ¼ 0 as (9.82). Compared to his it runs slower and slower at increasing

distances from the observer, and, since the vacuum speed of light is the same

constant if measured with proper time (9.78) and is deﬁning lengths (9.79), if he

sends out a light signal radially, it will propagate less and less distance, if less and

less of time is passing. At r ¼ c=x it seems to come to a halt. In fact it does not

propagate radially in the rotating coordinates. Instead its ray bends against the

direction of rotation and ﬁnally it nestles to the sphere r ¼ c=x. Similarly, a light

ray emitted from rotating matter inward is bent in the opposite direction.

The observer is unable to trace any process outside the radius c=x since any two

signals coming close in time from the same direction are originating from a-causal

events (separated by Ds \0). Nevertheless, the particular role of r ¼ c=x is solely

caused by the chosen rotating coordinate system. The physics is not special there,

and for instance det g, which is invariant under linear coordinate transformations,

in the considered case is regular in both systems, det g

¼ det g ¼ r

as directly

calculated from the above two expressions for ds

The observer at r ¼ 0 would see the same physics regardless whether he is

rotating or a gravitational ﬁeld is in effect which acts on all masses with a force

equal to the ﬁctitious forces of the rotating system in the domain r \ c=x: As

soon as he is able to be convinced to see real physical processes outside this

domain simply by changing his rotation frequency with respect to his reference

system, he can put an upper limit to such a gravitational ﬁeld and ﬁnally exclude

its existence by extending his observations to unlimited distances. So much

about the example.

Since the space-time manifold M (generalization of the Minkowski space) has

got a metric, the Hodge operator (4.89) may be deﬁned and applied to the external

calculus on M. Since det g \ 0, according to (4.87) and (9.47) the invariant

volume form is

s ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

^ dx

; ð9:84Þ

and the Levi–Civita pseudo-tensor (5.85)is

jklm

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

0123

jklm

; E

jklm

1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

0123

jklm

: ð9:85Þ

For various alternating tensors x,(5.87) now reads

9.6 Gravitation 331

ð1Þ

jklm

¼ E

jklm

;

ðxÞ

¼ E

jklm

jkl

; ðxÞ

klm

jklm

;

ðxÞ

jklm

; ðxÞ

jklm

;

ðxÞ

klm

jklm

; ðxÞ

¼ E

jklm

jkl

;

ð1Þ

jklm

¼ E

jklm

ð9:86Þ

These rules provide a duality between alternating tensors x of rank n and

alternating tensors x of rank 4 n. The dual d to the external differentiation d is

(5.90) for m ¼ 4:

dx ¼ðdðxÞÞ; ð9:87Þ

and for x; r 2D

ðMÞ; 0 n 4

½xjr¼

x ^r ð9:88Þ

is an invariant integral to which Stokes’ theorem can be applied. For contravariant

alternating tensors x the forms x of the right column of (9.86) are often called

tensor densities, which name, however, has no deeper meaning; the understanding of

tensor and tensor density may be interchanged in (9.88). Among many other things

these relations allow to apply readily the equations (5.96)to(5.101) and their

consequences to the case of Maxwell ﬁelds in the presence of a gravitational ﬁeld.

As is seen from (9.77), gravitation is related to deviations of space–time from

being ﬂat. In a ﬂat space-time, C

 0 for chosen coordinates, all free particles

move along straight lines of an inertial system of coordinates which means that no

gravitational ﬁeld is present (or it is exactly compensated in an accelerated ref-

erence system of the observer, as for instance in the case of an observer in a freely

falling lift; these two possibilities can principally not be distinguished). In order to

construct an action integral for the gravitational ﬁeld, one needs a scalar formed

from curvature of space–time. The Christoffel symbols cannot directly be used

since they are not covariant at all. Scalars can systematically be formed by con-

traction of tensors. The Riemannian curvature tensor (9.33) allows only for one

non-zero contraction

¼ g

jlkm

; R

¼ R

; ð9:89Þ

since contraction of the ﬁrst or last pair of indices of R

jklm

yields a vanishing result

due to the alternating behavior (ﬁrst line of (9.34)) and the remaining contractions

are equal up to a sign. The obtained Ricci tensor is symmetric due to the last line

of (9.34) and hence may have again a non-zero contraction, the curvature scalar

R ¼ g

: ð9:90Þ

332 9 Riemannian Geometry

Einstein’s action is

S½g¼

Rs; ð9:91Þ

where j is Einstein’s gravitational constant, but the prefactor is convention as long

as no interaction with matter is considered. However, the action integral would not

have a minimum unless this prefactor is positive. The volume form s was given in

(9.84). True, this action contains second derivatives of the potentials g

, however,

they can be eliminated by an integration by parts. The variation of this action

yields

d R

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g



¼ d g

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g



¼ R

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

þ Rd

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

þ g

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

With (9.25),

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

;

and the above variation may be cast into

d R

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g



¼ R





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

The last expression is a total derivative, which can be seen from calculating it in

normal coordinates at x

, where then the C

and the derivatives of the g

vanish

at x

. (See p. 315; rg ¼ 0, and for vanishing C

one has from (7.43)

o=ox

g ¼ og=ox

.) From (7.48), in normal coordinates,

¼ g





 g



In these expressions, dC

is the variation of C

under a variation of the metric

. Such a variation does not affect the second term on the right hand side of (7.38)

which only depends on the transition function between two local coordinate

systems. Hence, it drops out of the variation of (7.38), and from what remains it is

seen that unlike C

itself its variation is a tensor. (It measures the difference of two

parallel transported tensors along the same path element in different metrics and

hence takes the difference of two tensors in the same point of the manifold.) Thus,

is a vector, and since the left hand side of the above chain of equations is a

scalar, the right hand side must also be a scalar. This allows to write down this

relation in arbitrary coordinates as g

¼ w

. Now, from (9.91),

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

¼ oð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

det g

Þ=ox

, and this derivative can be omitted in the

variation of the action (9.91). For a free gravitational ﬁeld the ﬁnal equation of

motion is R

ð1=2ÞRg

¼ 0 or

9.6 Gravitation 333



¼ 0: ð9:92Þ

Linearization of this equation at g

0lm

, equal to the Minkowski metric (9.74),

that is, linearization in h

from g

¼ g

0lm

þ h

, yields the wave equation hh

ðo=octÞ



ðo=ox



¼ 0 for gravitational waves in vacuum. With (9.85–

9.87) it is a simple exercise to get the relation ðdxÞ

¼ð1=2Þg

ðo=ox

Þx

for an

alternating tensor ﬁeld x and a homogeneous metric, g

¼ const. Hence,

ðddxÞ

¼ð1=2Þg

=ðox

Þx

, from which ðddÞ

¼ð1=2Þg

=ðox

results. Similarly, ðddÞ

yields the same result. That means that the d’Alembert

operator h for a homogeneous metric is to be replaced by the Laplace–Beltrami

operator ðdd þ ddÞ in covariant relations for an arbitrary metric. Therefore, ðdd þ

ddÞh

¼ 0 is the wave equation for the propagation of gravitational waves on top

of any gravitational ﬁeld.

If in addition to a gravitational ﬁeld matter ﬁelds are present, then similar to

(9.91) an action integral

s ð9:93Þ

may additionally be introduced with again a prefactor of convention and of setting

an energy scale, where T

is the energy–momentum tensor of matter. Its

expression for various forms of matter can be found in theoretical physics text-

books. (T

=c is an energy density in 3-space, and its multiplication with the

4-volume gives an action.) The mere demand of covariance couples matter to the

gravitational potential g

. (By using anti-commutators in the symmetry group,

gravity as supergravity becomes a Yang–Mills theory and hence a gauge ﬁeld

theory [5, Chapter 18].) Varying g

in the sum of (9.91) and (9.93) yields

Einstein’s ﬁnal ﬁeld equations for the gravitational ﬁeld as



; R ¼

T; R





ð9:94Þ

in which the energy-momentum tensor appears as the source term for gravitation

as phenomenologically expected. The second and hence the third equation simply

follow from tensor contraction of the ﬁrst. Note that this equation, on which

nowadays the construction of highest resolution GPS is based, was established

prior to all experimental observations of its consequences.

Let

¼ 1 þ

; g

¼ 0; g

¼d

1 



;

 1; ð9:95Þ

334 9 Riemannian Geometry

and let T

¼ mc

dðrÞ¼T; r ¼ðx

; x

Þ be the only non-zero component of the

energy-momentum tensor for a point particle of mass m at rest at the coordinate

origin. Then, from the last equation (9.94),

jmdðrÞ; R

¼ R

¼ 0; R

¼d

jmdðrÞ:

From (7.48) and (9.23), in lowest order of 1=c,

 R



Du R

with the Laplacian D. Hence,

Du ¼

dðrÞ¼4pkmdðrÞ; j ¼

8pk

; ð9:96Þ

which is Newton’s law, if k is Newtons phenomenological gravitational constant.

This ﬁnally determines Einstein’s constant in (9.91).

A solution of (9.96)isuðrÞ¼km=r. It has a singularity at r ¼ 0, and for

an observer on a world line x

ðsÞ proper time and length element (9.78, 9.79)

are

dt ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 

2km

; dl

¼ 1 þ

2km



i¼1

ðdx

Although (9.96) is the right equation for the gravitational ﬁeld of a point

charge only in lowest order in 1=c and hence only for large enough

distances from the center r ¼ 0 (in truth, in modiﬁed coordinates ðr; h; /Þ in

which 2pr means the length of a circle centered at the mass center so

that due to the curvature r is not any more the proper radius, dl

¼ dr

ð1  2km=ðc

rÞÞ þ r

ðsin h d/

þ dh

Þ), a qualitative feature is retained in the

solution of the exact equation: there is a horizon, the Schwarzschild radius

¼ 2km=c

at which dt vanishes for any world line x

ðsÞ. A clock on this

world line becomes so fast that any motion with velocity v c measured with

this clock seems to come to a halt. No passing of the horizon by matter or

light seems to be possible. The latter is indeed what happens with matter or

light from smaller radii. However, in the above mentioned exact Schwarzschild

solution of the problem, g

and hence dl

diverges at the same radius r

, and all

world lines of matter are bent inward for r\r

, which radius thus can be passed

only in one direction. Although g

and g

are singular in the chosen coordi-

nates, det g for the exact solution has again no singularity there. For an observer

from outside, in regularized coordinates the surface of the r

-sphere shrinks to a

point in which all information approaching it disappears. Inside r

no materi-

alizable rest frame exists. All matter moves eventually only further inward; there

is no cone of future opening outward from r

. If for a real spherical mass

9.6 Gravitation 335

distribution of high enough mass density q there is a solution of r ¼ r

ðmðrÞÞ,

where mðrÞ is the total mass inside r, then this situation of a black hole is

realized. Even at large enough values of r for which (9.96) is justiﬁed,

clocks, for instance atomic vibrations, slow down with increasing r. For an

observer at a ﬁxed value r

; r

\r light from atomic spectra at r arrives

at r

red shifted and its rays are bent. This gravitational red shift and bend-

ing from the earth’s mass has to be taken into account in the high resolution

GPS.

9.7 Complex, Hermitian and Kählerian Manifolds

Throughout this text real manifolds were considered with differentiable structures

(complete atlases) for simplicity assumed smooth although many statements on

manifolds generalize to less restrictive cases of C

-manifolds for sufﬁciently large

m (between 0 and 3 for most statements). If M has a complete atlas of coordinate

neighborhoods U

which are homeomorphic to open sets U

2 C

in such a way

that all transition functions u

 u

1

: u

ðU

\ U

Þ¼U

\ U

! U

\ U

ðU

\ U

Þ, are analytic (C

), then M is called an m-dimensional complex

manifold.

Recall from complex function theory, that a complex function Fðz

; ...; z

Þ¼

Re Fðx

; y

; ...; x

; y

Þþi Im Fðx

; y

; ...; x

; y

Þ; z

¼ x

þ iy

is analytic (ho-

lomorphic) at point ðz

Þ, iff it obeys the Cauchy–Riemann conditions

oRe F

oIm F

;

oRe F

¼

oIm F

; j ¼ 1; ...; m; ð9:97Þ

or iff it can be Taylor expanded in a neighborhood of ðz

Þ. If a mapping is analytic

and a homeomorphism, then the inverse mapping exists and is also analytic. Recall

also that a complex function F analytic on some domain cannot assume an extremal

absolute value jFj at an inner point of that domain unless it is a constant. Hence, any

analytic mapping of a compact, connected complex manifold without boundary into

the C

must be a mapping to one single point of C

. This gives some ﬂavor of how

restrictive the condition of analyticity on complex manifolds is.

As the simplest example, consider a two-dimensional oriented real manifold M

with a Riemannian metric ds

¼ðx

þðx

, where x

are two 1-forms on M,

in a coordinate neighborhood given by x

¼ x

ðx; yÞdx þx

ðx; yÞdy. A complex-

valued 1-form x in two real dimensions is called an analytic 1-form, if it can be

written as x ¼ f ðzÞdz; z ¼ x þ iy, with an analytic complex function f . If in the

above metric x

þ ix

is analytic, then ds

¼ðx

þ ix

Þðx

 ix

Þ is called an

analytic metric. This metric can be written as

¼jf ðzÞj

dzdz ¼jf ðzÞj

ðdx

þ dy

Þ: ð9:98Þ

336 9 Riemannian Geometry