Еремеев В.А., Зубов Л.М. Основы механики вязкоупругой микрополярной жидкости

Подождите немного. Документ загружается.

Глава 1

Кинематика континуума Коссера

Микрополярный континуум представляет собой сплошную среду,

в которой каждая частица обладает шестью степенями свободы аб-

солютно твердого тела [32, 45, 92, 101, 119, 120, 126, 151, 155]. Каж-

дая частица микрополярной сплошной среды помимо обычных транс-

ляционных степеней свободы обладает также ориентационными, или

вращательными, степенями свободы.

В текущей, или актуальной, конфигурации в момент времени t по-

ложение частицы микрополярного тела описывается радиус-вектором

R, а ее ориентация задается при помощи трех ортонормированных

векторов D

(k = 1, 2, 3), которые называются директорами. Эти век-

торные поля и определяют трансляционные и вращательные степени

свободы частиц тела.

Для описания деформации рассмотрим некоторое фиксированное

состояние тела, например, но не обязательно, взятое при t = 0, кото-

рое назовем отсчетной конфигурацией. В этом состоянии положение

частиц определяется при помощи радиус-вектора r, а ориентация –

директорами d

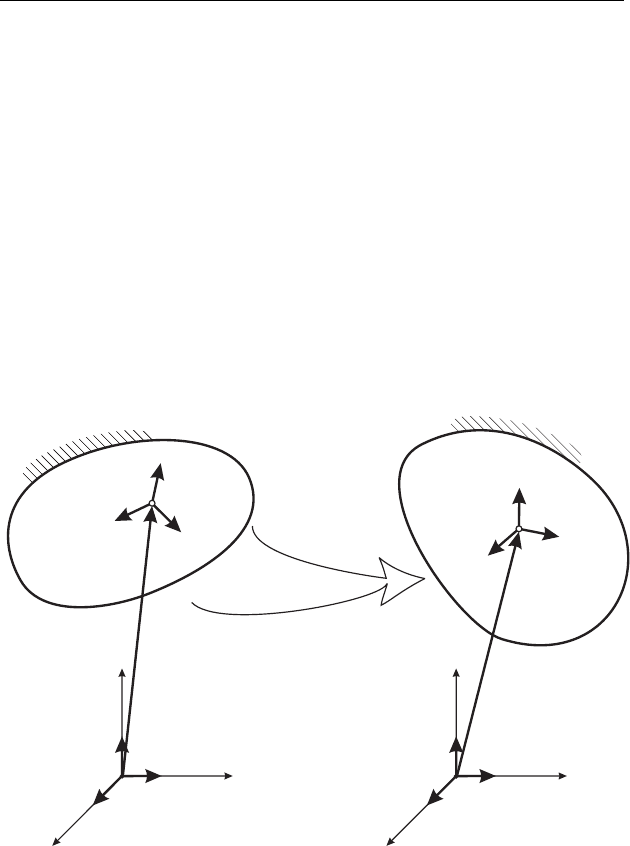
(рис. 1.1). Движение микрополярной среды может

быть описано при помощи векторных полей

R = R(r, t) , D

= D

(r, t). (1.1)

Поскольку в процессе деформации директоры D

остаются ортонор-

мированными, их изменение может быть представлено при помощи

ортогонального тензора

H = d

⊗ D

1.1. 11

называемого тензором микроповорота. Предполагается, что векторы

, D

, а также векторы d

, d

образуют правые тройки. По-

этому H является собственно ортогональным. Следовательно, дефор-

мация микрополярной среды может также быть описана при помощи

следующих отображений

R = R(r, t), H = H(r, t). (1.2)

Поскольку кинематика микрополярной сплошной среды отличает-

ся от простых материалов наличием дополнительных векторных или

тензорного полей, то отображения (1.1) или (1.2) порождают меры

и тензоры деформации, вообще говоря, отличные от используемых в

классической механике сплошной среды.

C, H

Рис. 1.1. Движение микрополярного тела.

12 Глава 1. Кинематика континуума Коссера

1.1 Меры и тензоры деформаций в континууме Коссе-

ра

Для введения мер и тензоров деформации рассмотрим бесконечно

малые приращения величин, описывающих движение микрополярно-

го тела.

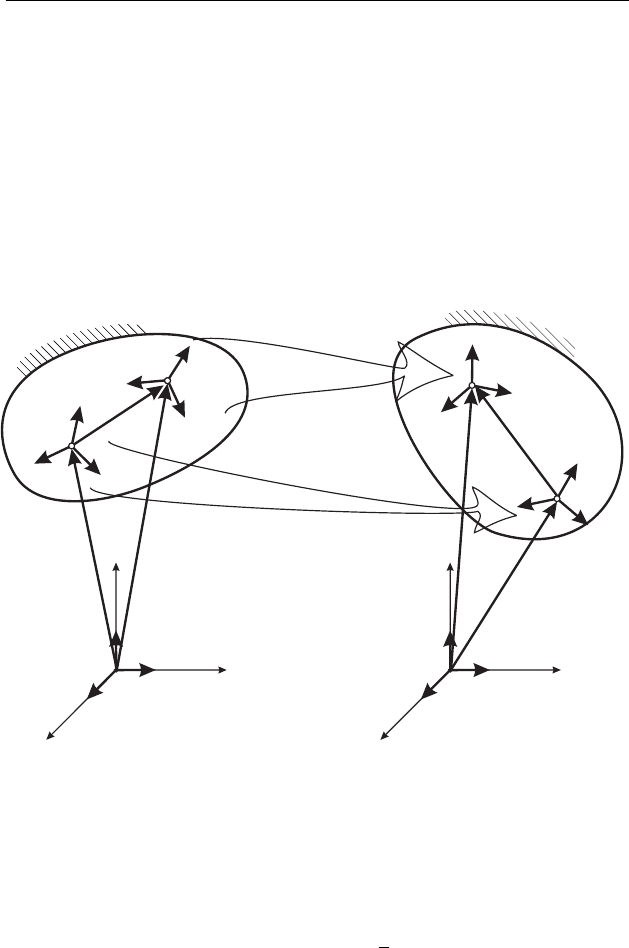
Градиент деформации C ≡ grad R связывает бесконечно малые

приращения радиус-вектора частиц тела в отсчетной и актуальной

конфигурациях:

dR = dr · C. (1.3)

R + dR

r + dr

C, H

Рис. 1.2. Деформация микрополярного тела.

Рассмотрим далее приращения директоров D

в актуальной кон-

фигурации. Поскольку D

единичны, то вектор dD

будет ортогона-

лен к D

. Отсюда следует представление

= B

× dD

, B

× dD

. (1.4)

1.1. Меры и тензоры деформаций в континууме Коссера 13

Соотношение (1.4) позволяет ввести тензор B следующим формулой

= d

(1.5)

Отсюда следует, что

B = −

(Grad D

) × D

. (1.6)

Тензор B можно назвать тензором кривизны микроструктуры

актуальной конфигурации, поскольку он описывает изменение трие-

эдра директоров D

в этой конфигурации.

Рассматривая приращения директоров d

в отсчетной конфигу-

рации, аналогично можно ввести тензор кривизны микроструктуры

b отсчетной конфигурации

= b

× d

, b

× dd

, b

= dr · b, (1.7)

b = −

(grad d

) × d

В (1.6) и (1.7) Grad и grad – операторы градиента в актуальной

и отсчетной конфигурациях. Тензоры B и b описывают локальноe

изменение директоров в актуальной и отсчетной конфигурациях со-

ответственно.

Найдем приращение тензора микроповоротов H. Выполняются со-

отношения

dH = d(d

⊗ D

= ( dd

) ⊗ D

+ d

⊗ dD

= (1.8)

= b

× d

⊗ D

− d

⊗ D

× B

= dr · b × H − H × B

· dR =

= dr · b × H − H · ( dr · C · B × I).

Используя (1.4)–(1.7), из (1.8) получим формулу

( dH) · H

= dr · (b − C · B · H

) × I, (1.9)

где I – единичный тензор.

Учитывая, что по определению градиента выполняется равенство

dH = dr · grad H,

14 Глава 1. Кинематика континуума Коссера

из (1.9) вытекает формула для градиента тензора микроповорота

grad H = (b − C · B · H

) × I. (1.10)

При деформации частицы микрополярного континуума испыты-

вают не только трансляционные перемещения, но и повороты, кото-

рые, в отличие от простого нелинейно упругого тела, вообще говоря,

не связаны с тензором макроповорота (C · C)

−1/2

· C, являющимся

ортогональным сомножителем в полярном разложении градиента де-

формации [48, 61]. Ориентация частиц в пространстве задается при

помощи тензора микроповорота H. Найдем разность dR − dr · H.

Получим

dR − dr · H = dr · (C − H). (1.11)

Меры и тензоры деформаций естественно связать с нормами рас-

сматриваемых приращений. Используя евклидову норму, получим

kdR − dr · Hk

= dr · (C · H

− I) · (H · C

− I) · dr, (1.12)

kdHk

= 2 dr · (C · B · H

− b) · (H · B

· C

− b

) · dr. (1.13)

Формула (1.12) следует из (1.11), а (1.13) получается из (1.9) c

учетом равенств kdHk = k( dH)·H

k и kWk =

√

2kwk, выполняюще-

гося для любого антисимметричного тензора W, связанного со своим

аксиальным вектором w формулой W = I × w.

На основании (1.12) и (1.13) eстественно ввести следующие тензо-

ры и меры деформаций типа Коши-Грина

E = C · H

− I, L = C · B · H

− b,

Y = C · H

, K = C · B · H

(1.14)

При отсутствии деформаций (R = r, H = I) тензоры деформаций

обращаются в нуль (E = L = 0), в то время как меры деформаций

нет (Y = I, K = b).

Следует отметить, что соотношения (1.12), (1.13) в принципе поз-

воляют ввести несимметричные тензоры деформаций бесчисленным

числом способов. Выбранный здесь связан с тем обстоятельством, что

как будет отмечено ниже, такие же меры и тензоры деформации могут

1.2. Меры и тензоры деформаций в континууме Коссера 15

быть введены на основе и других идей, не связанных с рассмотрением

бесконечно малых приращений.

Через Y также выражается изменение длины элементарного во-

локна:

kdRk

− kdrk

= dr · (Y · Y

− I) · dr. (1.15)

Отметим, что соотношение (1.15) вместе с равенством

C = Y · H (1.16)

позволяет считать Y аналогом правого тензора растяжения в нели-

нейной теории упругости простых материалов, однако уравнение

(1.16) не является полярным разложением градиента деформации C,

и Y – несимметричный тензор.

Соотношения (1.12), (1.13) можно записать в другом виде

kdR − dr · Hk

= dR · (I − C

−1

· H) · (I − H

· C

−T

) · dR, (1.17)

kdHk

= 2 dR · (B − C

−1

· b · H) · (B

− H

· b

· C

−T

) · dR. (1.18)

Уравнения (1.17), (1.18) позволяют ввести меры и тензоры деформа-

ций типа Альманзи

e = I − C

−1

· H, ` = B − C

−1

· b · H,

y = C

−1

· H, k = C

−1

· b · H.

(1.19)

В результате рассмотренных выше геометрических рассуждений

формулами

(1.14), (1.19) для континуума Коссера естественным образом были

введены первая мера деформаций Y и тензоры деформаций E, e, вто-

рая мера деформаций y, первая и вторая меры изгибных деформаций

K, k , тензоры изгибных деформаций L, `.

Следует заметить, что определенные таким образом меры и тензо-

ры деформаций для микрополярной среды могут быть введены и по-

другому, например, на основе дополнительных рассуждений с исполь-

зованием принципа материальной индифферентности (см., например,

[155]) или как сопряженные к соответствующим тензорам напряжений

и моментных напряжений. Подробное обсуждение мер деформации в

континууме Коссера дано в [143, 144]. В [143] кроме того приведен

обзор работ, в которых обсуждалось введение мер деформации в мик-

рополярном континууме.

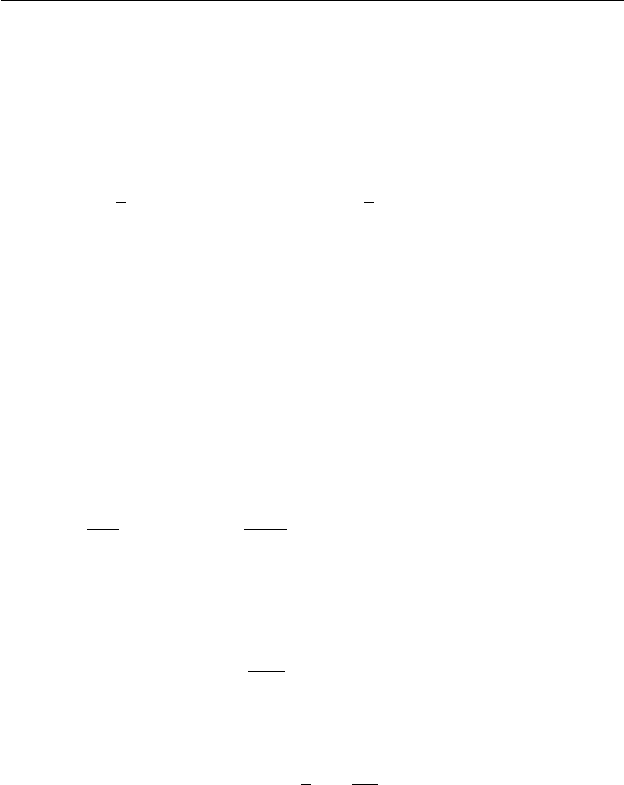
16 Глава 1. Кинематика континуума Коссера

1.2 Тензоры кривизны микроструктуры

Наряду с мерами и тензорами деформаций выше были также вве-

дены тензоры кривизны микроструктуры B и b в актуальной и от-

счетной конфигурациях, определяемые формулами

B = −

(Grad D

) × D

, b = −

(grad d

) × d

. (1.20)

Тензоры кривизны микростуктуры B и b не имеют прямых анало-

гов в механике простых тел и играют важную роль в механике микро-

полярного континуума. Если поля директоров постоянны D

= const,

= const, то b = B = 0.

Можно также показать, что B и b определяются через дифферен-

циальные связности.

Чтобы прояснить эту связь, предположим, что векторы D

свя-

заны с какой-то криволинейной ортогональной системой координат

, R

∂R

∂Q

, H

= |R

|, R

· R

= δ

Найдем вторые производные R. По определению символов Кри-

стоффеля Γ

имеем [22]

∂R

∂Q

= Γ

откуда с учетом предыдущих формул и определения B получим

· B · D

i,j

ijp

где ²

ijp

– символы Леви-Чивиты.

В общем случае неголономного базиса D

компонеты тензора B

также можно связать со связностями Γ

Знание тензорных полей B и b позволяет определить поля триэд-

ров D

и d

соответственно. Рассмотрим этот вопрос более подробнее.

1.3. Уравнения совместности для B 17

1.3 Определение направляющих векторов D

по задан-

ному полю тензора кривизны микроструктуры.

Уравнения совместности для B.

Следуя [49], рассмотрим задачу определения триэдра векторов

при заданном тензорном поле B(R), которое будем предполагать

непрерывно дифференцируемым. Обозначим через i

орты декарто-

вых координат X

и введем ортогональный тензор Q , D

⊗ i

. Так

как D

= Q·i

, то между триэдром D

и тензором Q имеется взаим-

но однозначное соответствие. Из (1.20) вытекает следующая система

уравнений для определения тензора Q при заданном поле тензора B

∂Q

∂X

= Π

· Q, Π

= I × B

, B

= i

· B. (1.21)

Необходимые и достаточные условия разрешимости системы (1.21)

относительно тензора Q имеют вид

∂B

∂X

∂B

∂X

+ B

× B

. (1.22)

Это соотношение можно записать в безкоординатном виде

(Rot B)

= B

− (tr B)B +

B − tr B

I. (1.23)

В случае неособого тензора B уравнение совместности (1.23) при

помощи формулы Гамильтона–Кэли можно записать иначе

(Rot B)

= B

−1

det B.

В односвязной области тройка ортонормированных векторов D

определяется по заданному гладкому тензорному полю B, удовлетво-

ряющему условию совместности (1.23), единственным образом, если

триэдр D

задан в некоторой точке области, а решение можно за-

писать при помощи мультипликативного криволинейного интеграла

[155]

Q =

∧

(I + dR · Π) · Q

, Q

= Q(M

), (1.24)

Π = i

⊗ Π

, dR = i

18 Глава 1. Кинематика континуума Коссера

В односвязной области формула (1.24) дает однозначное (т.е. не

зависящее от выбора пути, соединяющего точки M

и M) выражение

ортогонального тензора Q, определяющего ориентацию частиц жид-

кого континуума Коссера. Если область многосвязна, то несмотря на

однозначность тензорного поля B(R), тензорное поле Q(R), вообще

говоря, будет неоднозначным. Если провести разрезы (перегородки),

превращающие область в односвязную, то при пересечении каждого

из разрезов функция Q(R) может претерпевать скачок. Можно пока-

зать, что скачок описывается формулой

= Q

−

· Ω,

где Ω – постоянный для данного разреза и ортогональный тензор,

определяемый соотношением

Ω , Q

∧

(I + dR · Π) · Q

Здесь замкнутый контур мультипликативного интегрирования дол-

жен пересекать только одну перегородку.

1.4 Определение векторов D

вдоль кривой

Можно определить векторы D

по заданному полю тензора кри-

визны микроструктуры и в том случае, если тензор B задан не во

всем пространстве, а только на некоторой кривой. При этом выпол-

нение условий совместности от B не потребуется.

Рассмотрим в актуальной конфигурации произвольную гладкую

кривую L, заданную при помощи естественной параметризации R =

R(S) ≡ X

(S)i

, где S – длина дуги, i

– декартов базис. Опреде-

лим, как связано изменение триэдра D

вдоль кривой L с тензором

кривизны микроструктуры B и геометрическими характеристиками

кривой L. Обозначим через τ единичный вектор касательной к L.

Тогда τ = dR / dS.

Можно показать, что на кривой L выполняется соотношение

= τ ·B × D

= W · D

, (1.25)

1.4. Определение векторов D

вдоль кривой 19

Рис. 1.3. Изменение триэдра D

вдоль кривой.

где W

= τ ·B × I – антисимметричный тензор.

Действительно, имеем

∂D

∂X

× D

Учитывая, что τ =

и B = i

⊗B

, отсюда сразу следует

формула (1.25).

Если поле тензора кривизны микроструктуры задано на кривой

L, то (1.25) представляет собой систему обыкновенных дифференци-

альных уравнений, позволяющих определить триэдр D

на кривой

L по начальным данным, заданным в произвольной точке кривой:

) = D

. Например, если тензор W постоянный на кривой L

(W = W

), то из (1.25) следует формула

(S) = e

· D

Отметим важное следствие, следующее из (1.25). Имеет место