Elsevier Encyclopedia of Geology

Подождите немного. Документ загружается.

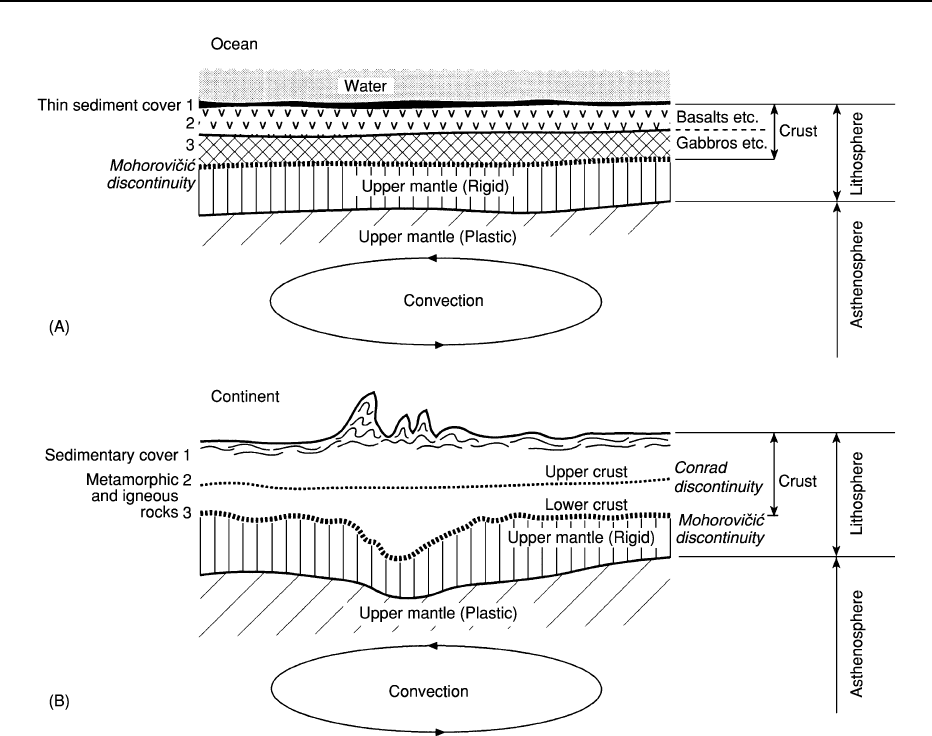
Recycling of the Crust

Plate tectonics requires that crustal slabs are recycled

in subduction zones and taken down to the mantle

(Figure 2). However, this is by no means an even

process, with oceanic crust being subducted very rap-

idly, but continental crust resisting recycling. The

result of this is that the oceans are all products of

the last plate dispersion cycle, which commenced

about the beginning of the Mesozoic, and no oceanic

crust is older than about 200 million years. In con-

trast, continental crust has been preserved almost

indefinitely, and there is some continental crust in

the Slave Province of Canada which is more than

4000 million years old. Minerals (zircons) in con-

tinental rocks in Western Australia are also up to

4300 million years old.

Physical Regions of the Crust

Continental crust is subdivided into a number of

physical regions.

Shields: deeply eroded expanses of low relief,

which have been stable since Precambrian times.

Platforms: similar to the above, but mantled by

thick sedimentary cover, which may be entirely or

in part Phanerozoic in age.

Orogens: long, curved belts of folded rocks, usually

forming mountain chains, mostly formed by con-

tinental collisions.

Rifts: linear, fault-bounded depressions, traversing

continents; these are the structures which originate

crustal splitting and dispersion, and lead to mid-

ocean ridge formation, but they may, as in the case

of the East African Rifts, be aborted, i.e., never

developed into oceans.

Oceanic crust is also subdivided into a number of

physical regions.

Volcanic islands: scatterings or chains of islands

which mark mantle hotspots.

Volcanic arcs: above subduction zones (e.g., Aleu-

tian Islands), these may be represented by their

Figure 1 Diagrams showing the threefold layering of the oceanic (A) and continental (B) crust. The continental crust is much thicker

than the oceanic crust. The two diagrams are not to scale.

404 EARTH/Crust

eroded underworks – chains of calc-alkaline batho-

liths (e.g., Peru).

Trenches: the outer margin of subduction zones;

the deepest parts of the oceans.

Ocean basins/abyssal plains: the extensive flat,

deep areas of oceans, beyond continental slopes.

Marginal basins: small basins separating arcs, or

landward from arcs (back-arc basins).

Inland seas: seas within continents (e.g., Caspian).

The relative area and volume of the major crustal

types are shown in Figure 3.

Crustal Structure

We can broadly determine the contrasting layers

in the crustal structure by means of seismic wave

velocities, determined from earthquake waves and

artificial (e.g., nuclear) explosions. This shows us

Figure 2 Diagram showing the recycling of the crust by subduction. After Edwards K and Rosen B (2000) From the Beginning. London:

Natural History Museum.

Figure 3 Area and volume proportions of the major crustal types. From Plate Tectonics and Crustal Evolution by K. C. Condie (1976).

Reprinted by permission of Elsevier Ltd.

EARTH/Crust 405

that there are three contrasting layers in the oceanic

crust and also three in the continental crust, but they

are different. In the oceanic crust, we can use analo-

gies with ‘ophiolites’ (see Tectonics: Convergent Plate

Boundaries and Accretionary Wedges), which have

been recognized as old oceanic crust, subducted and

later obducted onto the continental surface, where

they form bodies of surface rocks. Ophiolites are

present in surface rock assemblages of all ages, as

far back as the Archaean upper boundary (2500 Ma).

The three layers of the oceanic crust are believed

to comprise a sediment layer (0–1 km thick), a

basement layer (mainly basalt) (0.7–2.0 km thick),

and an oceanic layer (sheeted basaltic dykes, gabbros)

(3–7 km thick).

The continental crust can be divided into an upper

layer (10–20 km thick) and a lower layer (15–25 km

thick). Sedimentary cover, possibly up to several kilo-

metres thick, may or may not be present above the

upper layer. The boundary between the upper and

lower layer may be well defined by a change in seis-

mic velocities, although it may not be detectable. It is

called the ‘Conrad discontinuity’.

Chemical Composition

of the Crust

Much of the crust is buried, and we have no direct

access to the material from which it is composed;

therefore, much reliance must be placed on indirect

methods of determination.

Seismic Wave Velocities

An important method is based on the measurement of

seismic wave velocities, which indicate what mater-

ials are possible for any particular layer according to

density (see Seismic Surveys).

Chemical Analyses

The many different rock materials that make up the

continental shields can be analysed directly and

weighted according to observations of relative abun-

dance to give an average for the upper continental

crust. Fine sediments, such as clays, can be analysed,

being assumed to match closely the average com-

position of the upper continental crust. This assump-

tion is based on the fact that clays give consistent

values for thorium and rare-earth elements, which

are relatively insoluble in natural water; amounts of

such elements vary widely in concentration between

different rock types of the upper continental crust,

and this suggests that mixing in such fine-grained

sediments of the contributory source rocks is very

thorough.

Studies of Sections of Deep Crustal Rocks Exposed

by Tectonic Processes: Deep-Sourced Xenoliths in

Volcanic Rocks

There are some regions in which tectonic processes

have revealed sections of the crust, on end, so that a

geologist can traverse across the surface terrain, en-

countering progressively deeper crustal levels, includ-

ing deep metamorphic rocks, such as granulites, at the

surface. One such case is the Kapuskasing Belt in

Ontario, Canada. Such exposed sequences of the

deeper crustal rocks indicate that, in the deeper con-

tinental crust, below the Conrad discontinuity, there is

much variation in both the horizontal and vertical

dimensions, and that models invoking uniform

layering of, for example, a granulite layer are not

valid. The evidence from both exposed sequences

and deep-sourced xenoliths in volcanic rocks suggests,

besides heterogeneity, that the lower continental crust

is of more basic, less siliceous, composition than the

upper continental crust – that is, more rocks of bas-

altic composition are represented and metamorphic

granulites are characteristic.

Oceanic Crust

The composition of the oceanic crust can be derived

from the study of ophiolitic sequences, which have a

systematic layering from lavas at the top, through

sheeted basaltic dykes, to gabbros or layered diff-

erentiates of gabbroic magma below. Ophiolites can

commonly be studied in traverses on the ground,

through sections exposed on end, and even, as in

Oman and western Newfoundland, from exposures

of the oceanic crust–mantle boundary. Deep ocean

sediments are very thin and can be ignored in making

a weighted assessment according to the observed

abundance of these three components. Such an esti-

mate yields a basaltic composition for the oceanic

crust, but poor in K

The values derived from such methods and given in

Table 1 seem to be reasonable.

Table 1 Chemical composition (wt.%) of the crust

Component

Continental

upper layer

Continental

lower layer

Ocean

crust

SiO

65.5 49.2 49.6

15.0 15.0 16.8

TiO

0.5 1.5 1.5

FeO 4.3 13.0 8.8

MgO 2.2 7.8 7.2

CaO 4.2 10.4 11.8

O 3.6 2.2 2.7

O 3.3 0.5 0.2

Total 98.6 99.6 98.6

406 EARTH/Crust

Partial Melting within the Crust

At the mid-ocean ridges, where the oceanic crust is

thinnest, partial melting of the upper mantle material

leaves behind a depleted mantle. Some crustal ma-

terial may also suffer partial melting, modifying

the residual oceanic crust, but this is probably not a

major process, because the ascent of magma is rapid

here. However, in the island arc situations in the

overriding plate above the subducting plate, the erup-

tives that form the volcanic arcs and batholiths be-

neath them, mainly of calc-alkaline igneous rocks,

pass quite slowly through the quite thick crustal

rocks of the overriding plate; therefore, here there is

much mixture of partial melting products from both

mantle and crust, and the crust is always suffering

modification and displacement. This process makes

for a very heterogeneous continental crust at all levels.

Crustal Growth and Loss

The fact that some isotopically derived ages of con-

tinental crustal rocks are more commonly obtained

than others, e.g., 2700 Ma and 2000 Ma being par-

ticularly common, suggests that the rate of new

continental crust growth compared with loss by sub-

duction has not been constant through geological

time. This may be explained in terms of the plate

tectonics paradigm, but may also be explained, at

least partly, if plate tectonics processes did not oper-

ate or did not operate significantly in Archaean times

(something for which there is considerable evidence).

This is, however, an area of considerable uncertainty.

In any case, there are a number of processes by which

continents grow: (1) by continental plate collision

(which does not affect the overall total of continental

crust, but can cause crustal loss by metamorphism of

the deep roots of collision zones to denser PT-com-

patible mineral phases, gravitational instability, and

sinking to the mantle); (2) by underplating by basaltic

magma from mantle hotspots or plumes (assuming

that plumes do exist), or surface eruption therefrom

to form lava plateaux (e.g., the Deccan); (3) by the

addition of ophiolite material of old oceans; (4) by

obduction onto continental edges; or (5) by collisions

with oceanic terranes (islands, island arcs, submarine

plateaux). The return process may be the direct sub-

duction of continental slabs, or a three-stage process

of erosion of continental crustal material, deposition

of it as sediments, and their subduction.

Oceanic crust is either rapidly subducted or lost to

continents by obduction onto their edges or by colli-

sions of terrains with continents as mentioned above.

It does not have a protracted geological history as

does continental crust. It can, however, be added to

during its relatively ephemeral history by the addition

of magma from mantle hotspots or plumes beneath

(e.g., Ontong-Java Plateau).

The Primitive Crust

It is widely believed that the early Earth possessed a

primitive globe-encircling basaltic crust. The pre-

sent surfaces of Mercury, the Moon, or Mars may

provide an analogue as they have apparently never

experienced plate tectonics and there is evidence

suggesting a basaltic surficial shell still covering the

whole of Mars (see Solar System: Mars). We now

know that there must have been some continental

crust very early in the Earth’s history, the evidence

being in the form of zircons of continental crust prov-

enance up to 4300 Ma at Mt Narryer in western

Australia. The process of continental crust formation

has been compared to a scum or slag of light material

forming on the surface of a basaltic melt, repeated

again and again, until extensive continents emerged

after a repetition of cycles. Thick continental blocks

appear to have been in place by 3500 Ma, being rep-

resented by the oldest cratons of South Africa and

Australia, but the earlier protocontinents were prob-

ably small and thin. This is as far as we can go at the

present state of knowledge.

The Crust and Isostasy

The concept that gravitational equilibrium controls

the heights of continents and ocean floors was pro-

posed by Dutton in America in 1889. The analogy

with wooden blocks floating in water was elegantly

illustrated by Holmes in 1965 (Figure 4). The concept

is one of hydrostatic balance, the Earth’s major relief

being compensated by the underlying differences in

density, whereas minor relief features are compen-

sated by the strength of the underlying rock. The

compensation depth was traditionally placed at the

Moho, but the plate tectonics paradigm necessitates a

rethink of this. Isostasy is, however, a real crustal

process and can be seen in action in the central sag

of Greenland under the weight of the enormous

Figure 4 Representation of isostasy using floating wooden

blocks of unequal dimensions. Reproduced with permission from

Holmes A (1965)

Principles of Physical Geology. London: Nelson.

EARTH/Crust 407

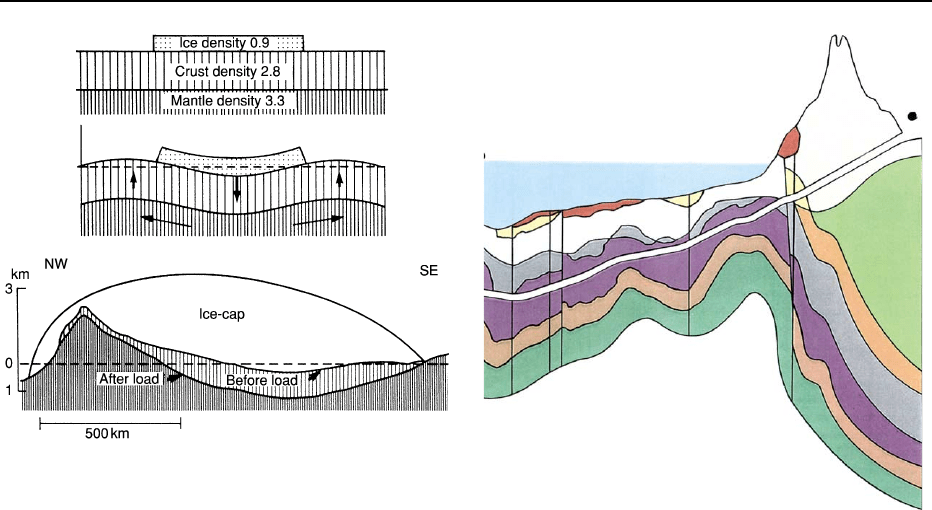
Figure 5 The Earth’s crust floats on a dense mantle that be-

haves as a viscous liquid. If we place an ice-cap on it, enough

mantle material is displaced sideways to equal the additional

crustal load, and a low broad welt is raised peripheral to the

ice-cap. The mantle adjustment is very slow, so that depression

and rebound after removal of the ice-cap are delayed. The situ-

ation at present in Greenland is shown in the lower part of the

figure, and the delayed rebound is being experienced in the

Baltic. From Van Andel TJ (1994)

New Views on an Old Planet.

Cambridge: Cambridge University Press.

Figure 6 A sectional diagram of the French entry section to the

Channel Tunnel showing tectonic deformation (folding, faulting)

of the Cretaceous and Quaternary strata of the crust. Extract from

BREAKTHROUGH by Derek Wilson published by Century Hutch-

inson. Reproduced from The Random House Group Limited.

ice-sheet which has sagged below sea-level in places

(Figure 5), and also in the rebound occurring now in

the Baltic after the ice-sheet has gone – the renowned

Swedish geologist, Harry von Eckerman, used to go

to the Alno

Island carbonatite complex yearly to see

what new rocks had surfaced due to this rebound.

Heat Flow to the Crustal Surface

The continental surface heat flow is linearly related to

the heat productivity of the near-surface granitic

rocks. Variability from region to region is mainly

related to the distribution of near-surface radioactiv-

ity, derived from certain minerals in the granitic

rocks. Most models favour an exponential decrease

in radioactive heat source with depth in the continen-

tal crust and a residual amount of heat rising from

the upper mantle. The weighted average heat flow

from both continental and oceanic crust is 1.5 heat

flow units (HFU). This equivalence is explained by

the heat flow to the oceanic crust surface coming

mainly from the mantle, whereas it comes mainly

from radioactive minerals in the crust at the contin-

ental surface. This requires increased radioactive

sources in the mantle under the oceans, or that con-

vective heat from the mantle under the oceans

happens to equate to the radioactive-sourced heat

from the continental crust, or that the mantle-derived

convective heat is much the same under continental

and oceanic lithosphere, but the thicker continental

lithosphere is more depleted in radioactive heat

sources than the oceanic lithosphere. The latter is

preferred because it allows equal movements of both

continental and oceanic crust-dominated plates.

Crustal Deformation

The crustal rocks of the Earth are subject to many

and diverse deformation processes. The most signifi-

cant are ‘tectonic’ processes (folding and faulting;

Figure 6), which act very slowly through long periods

of geological time and are mostly related to the move-

ment of tectonic plates (especially collision and sub-

duction). Stress on faults is subject to long build-up,

but may be relieved by abrupt, almost instantaneous

dislocation (which may form a linear earthquake

scarp on the surface; Figure 7), or prolonged dissipa-

tion by creep movements without any earthquake.

Earthquake foci are mostly situated within the crust,

but some, especially those in margins of continental

areas of plates, may have foci several hundred kilo-

metres deep, within the mantle (see Tectonics: Earth-

quakes).

In contrast with tectonic deformation, ‘superficial’

deformation of the crust, such as landsliding, sink-hole

formation, and submarine slumping, occurs abruptly,

within a matter of seconds, minutes, hours, or days

(Figure 8)(see Sedimentary Processes: Landslides).

408 EARTH/Crust

Conclusion

The Earth’s crust is the site of the great majority

of processes studied by geologists, and thus is

better known and understood than the mantle or

core. However, there remain aspects of uncertainty,

particularly the mechanisms of plate movement and

earthquakes, and the exact nature of the lower parts

of the crust.

Further Reading

Condie KC (1976) Plate Tectonics and Crustal Evolution.

New York, Toronto, Oxford, Sydney, Braunschweig,

Paris: Pergamon Press.

Edwards K and Rosen B (2000) From the Beginning.

London: Natural History Museum.

Goudie A (1989) The Nature of the Environment. Oxford:

Blackwell.

Hancock PL and Skinner BJ (2000) Oxford Companion to

the Earth. Oxford: Oxford University Press.

Holmes A (1965) Principles of Physical Geology. London:

Nelson.

Stamp LD (1951) The Earth’s Crust. London, Toronto,

Wellington, Sydney: GGHarrap.

Van Andel TJ (1994) New Views on an Old Planet.

Cambridge: Cambridge University Press.

Figure 7 A low fresh scarp of the Nojima Fault, Awaji Island, caused by the Kobe Earthquake, Japan, 1995. This was the almost

instantaneous product of relief of one of many successive prolonged build-ups of stress on an active fault. Reproduced with permission

from Esper P and Tachibana E (1998) The Kobe Earthquake. In: JG Maurel and M Eddleston (eds.) Geohazards in Engineering Geology,

Geological Society of London Engineering Geology Special Publication 15

, pp. 105–116. London: Geological Society.

Figure 8 Classification of superficial mass movements on

slopes and examples of some major types. Reproduced with

permission from Goudie A (1989)

The Nature of the Environment.

Oxford: Blackwell.

EARTH/Crust 409

Orbital Variation (Including Milankovitch Cycles)

HPa

like, Stockholm University, Stockholm, Sweden

Introduction

Earth’s orbital variations, caused by the mutual gravi-

tational interaction between the sun, the planets, and

their satellites, have been invoked as a mechanism for

long-term variations (time-scales of 10

–10

years) of

Earth’s climate system. The orbital variations are

known as ‘Milankovitch cycles’,aftertheSerbian

mathematician Milutin Milankovitch. In this article,

the relationships between the different parameters that

affect orbital variations are explored, with a further

view towards long-term patterns.

Celestial Mechanics

The time-varying motion of the planets and other

satellites around the sun and around each other is

controlled by mutual gravitational interactions. This

relationship can be described by Newton’slaws,cor-

rected by Einstein’s principles of general relativity. The

overall behaviour of the entire solar systemis even more

complex; it is posed as an N-body problem (which is

solved numerically), and is further complicated by

physical parameters such as the tidal dissipation of

energy and the detailed and changing distribution of

mass within each body. Given this complexity, the

planets do not follow stationary orbits around the

Sun, but rather undergo perturbed quasiperiodic vari-

ations that, from a climatic point of view, this affects the

amount, distribution, and timing of solar radiation

received at the top of Earth’s atmosphere. Milutin

Milankovitch explained glaciations and de-glaciations

(on time-scales of 10

–10

years) by variations of

solar radiation distribution at the top of Earth’s atmos-

phere, coupled with the latitudinal distribution of

land masses on Earth (see Palaeoclimates).

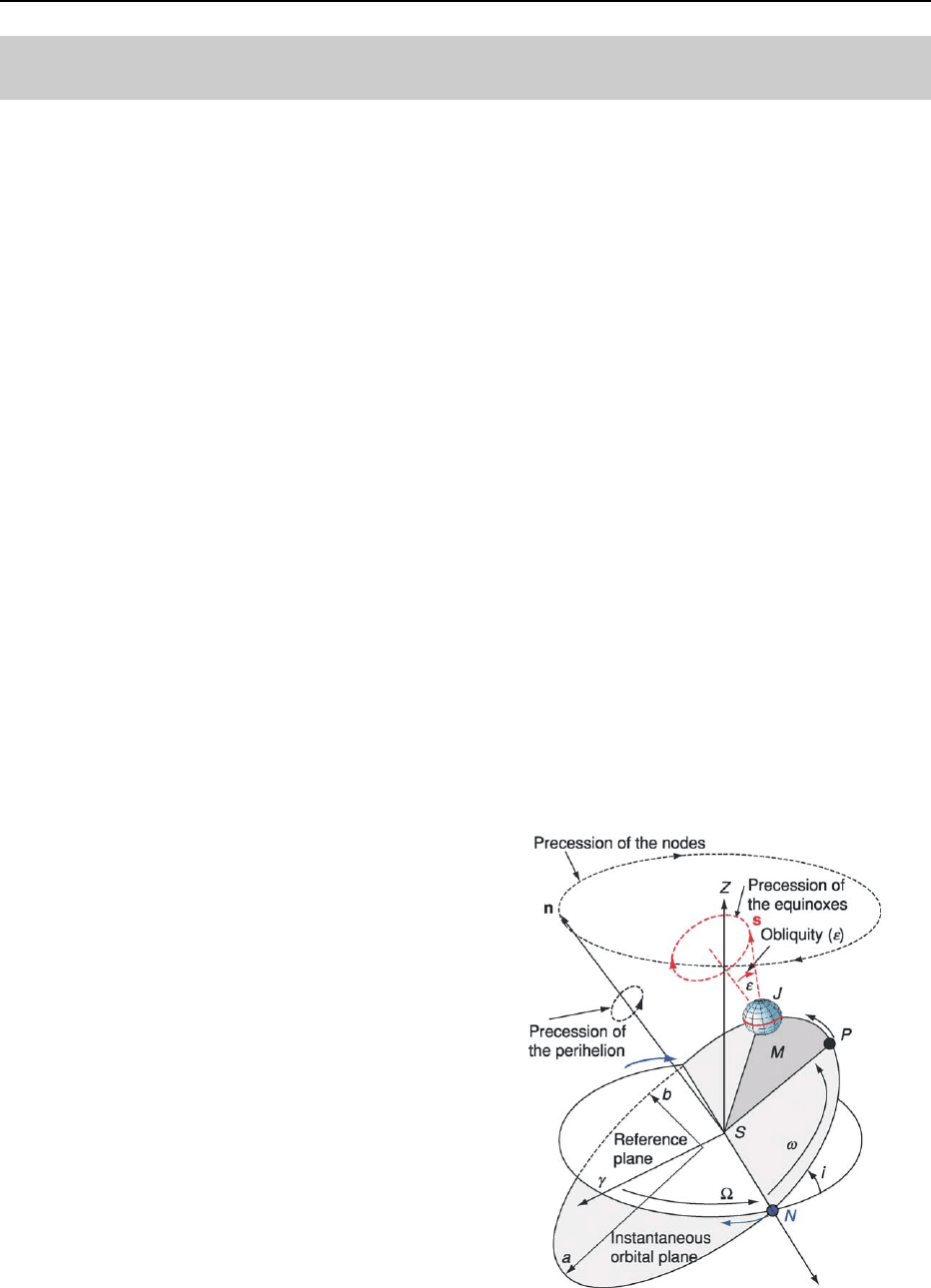
At any given time, the orbit of a body can be de-

scribed by six parameters. These parameters define

the position, shape, and orientation of an orbit and

the location of a body in the orbit, with respect to a

frame of reference. The trajectory of the orbiting body

follows an ellipse; in the case of the Solar System, the

sun is located at one focal point. Due to gravitational

interactions between the different planets, the orien-

tation and dimension of the ellipse change over time.

Figure 1 illustrates how the relationships between the

six ‘Keplerian orbital elements’ (a, e, i, l,

o, and O)

apply to Earth in its orbit. A reference plane is fixed

with respect to the stars; it is typically chosen as the

orbital plane of Earth at a particular time (say, ad 1950

or 2000) and is called the ‘ecliptic of date’.Alterna-

tively one can choose a plane perpendicular to the

total angular momentum of the Solar System (the ‘in-

variant’ plane). The ‘invariant’ plane almost coincides

with the orbital plane of Jupiter due to its large mass.

The reference plane is defined by two axes, both ori-

ginating from the position of the Sun (S; Figure 1)on

the reference plane. One of these, g, is typically the

position of the mean vernal (spring) equinox on the

reference plane at a given time; the second axis, Z,is

perpendicular to g as well as to the reference plane. The

parameter a, the semi-major axis of the orbital ellipse,

corresponds to the average radius. The eccentricity e of

the ellipse is defined as e ¼ (a

 b

)

1=2

/a,whereb is

the semi-minor axis of the ellipse. The inclination of the

orbit with respect to the reference plane is given by

the angle i. The position of the ascending node N is

specified by the angle O (‘longitude of the node’), meas-

ured from the fixed direction in the reference plane (g).

The parameter

o specifies the position of the moving

perihelion P (the closest approach to the Sun) and is

defined as

o ¼ O þ o (‘longitude of the perihelion’).

Finally, the sixth Keplerian element, l, specifies the

position of the orbiting body (J) on its elliptical orbit,

and is defined as l ¼ o þ M, where the mean anomaly

M is an angle that is proportional to the area SPJ

(Kepler’s third law).

Figure 1 Orbital elements of the Earth’s movement around

the Sun.

410 EARTH/Orbital Variation (Including Milankovitch Cycles)

Origin of Orbital Frequencies

If Earth were the only planet orbiting the sun, and in

the absence of dissipative effects and other physical

processes, the position and orientation of its orbit

would remain fixed for all times. In this situation,

the only Keplerian element that would change over

time is l, which describes the position of a body in its

orbit. In this case, the position and velocity of the

orbiting body would vary according to the Keplerian

laws of motion around a fixed ellipse. However,

gravitational interactions between all bodies of the

Solar System cause changes in the shape and orienta-

tion of the elliptical orbit on various time-scales,

which are typically of the order of 10

–10

years.

From a long-term climatic point of view, the relevant

variations are those obtained after averaging the

planetary orbits over their long-term orbital periods.

These are termed ‘secular variations’, and they can be

related to a set of fundamental frequencies. Variations

in the orbital elements that characterize the secular

variations can be separated into two categories that

are related to different types of precession move-

ments. The first category, variation within an orbital

plane, is described by the variation of the eccentricity

e and the rotation of the location of the perihelion

(described by o). The second category, variation of the

orientation of an orbital plane, is described by the

inclination angle i and the location of the ascending

node N (described by O). These oscillations are

coupled such that it is possible to investigate the be-

haviour of these parameters as pairs: (e, o)and(i, O).

Fundamental Frequencies of the Solar System

Computing the orbital elements for the eight main

planets (Pluto can be excluded due to its small mass)

obtains eight characteristic modal frequencies for

each of the paired elements (e, o)and(i, O). Table 1

illustrates these fundamental frequencies, estimated

over the past 20 My. Individual frequencies g

are

related to variations in the pair (e, o), whereas fre-

quencies s

are related to variations in the pair (i, O).

The individual g

and s

frequencies arise as eigen-

values from a matrix of linear differential Lagrange/

Laplace equations that are used to expand the orbital

elements for the eight planets. As eigenvalues of a

matrix, they are not strictly associated with a particu-

lar planet. However, because the matrix from which

they are obtained has a rear-diagonal structure, sup-

pressing a planet removes one set of frequencies but

does not change the other frequencies significantly.

Thus, the indices g

, s

can be used to indicate which

planet provides the strongest contribution to a particu-

lar frequency (indices g

, s

correspond to Mercury;

indices g

, s

correspond to Earth; and so on). Note

that all of the g

terms are positive, indicating that the

perihelia advance counterclockwise if viewed from the

‘north’ of the orbital axis shown in Figure 1.Incon-

trast, seven out of the eight s

terms are negative, indi-

cating that the positions of the nodes, which mark the

intersection of the orbital plane with the reference

plane, regress (rotate clockwise). Due to considerations

of angular momentum the eighth frequency is set to

zero, and by conversion is chosen to be s

because the

invariant plane is close to the orbital plane of Jupiter,

due to Jupiter’s large mass (see Solar System: The Sun;

Asteroids, Comets and Space Dust; Meteorites; Mer-

cury; Venus; Moon; Mars; Jupiter, Saturn and Their

Moons; Neptune, Pluto and Uranus).

General Precession of Earth

In addition to the fundamental orbital frequencies,

which apply to the Solar System as a whole, two addi-

tional fundamental frequencies are necessary to

Table 1 Fundamental orbital frequencies

Related to (e, o) Related to (i, O)

Term Frequency (

year

1

) Period (ky) Term Frequency (

year

1

) Period (ky) Associated planet

5.596 231.0 s

5.618 230.0 Mercury

7.456 174.0 s

7.080 183.0 Venus

17.365 74.6 s

18.851 68.7 Earth

17.916 72.3 s

17.748 73.0 Mars

4.249 305.0 s

0.000 Jupiter

28.221 45.9 s

26.330 49.2 Saturn

3.089 419.0 s

3.005 431.0 Uranus

0.667 1940.0 s

0.692 1870.0 Neptune

Fundamental orbital frequencies of the precession motions in the Solar System, computed as mean values over 20 million years.

The g

and s

are eigenvalues that characterize the evolution of the orbital elements (e, o) and (i, O), respectively, and are loosely

associated with the eight planets considered; i.e., the indices

, s

correspond to Mercury, and the indices g

, s

correspond to

Neptune. The period

a, in years, can be calculated from the frequency, in arcseconds (

) per year, as a ¼ (360  60  60)/

year

1

Data from Laskar J (1990) The chaotic motion of the Solar System – a numerical estimate of the size of the chaotic zones.

Icarus 88(2):

266–291.

EARTH/Orbital Variation (Including Milankovitch Cycles) 411

describe the orbital motion of Earth. The formation

of an equatorial bulge is caused by the rotation of

Earth, and other processes (e.g., the formation of

ice-caps at high latitudes and mantle convection) re-

distribute mass on Earth. These processes result in a

torque that is applied to Earth by the Sun, the Moon,

and the other planets. Approximately two thirds of

the torque is caused by the Moon, and one third by the

Sun. Similar to a spinning top, this applied torque

results in the nutation and precession of Earth’s spin

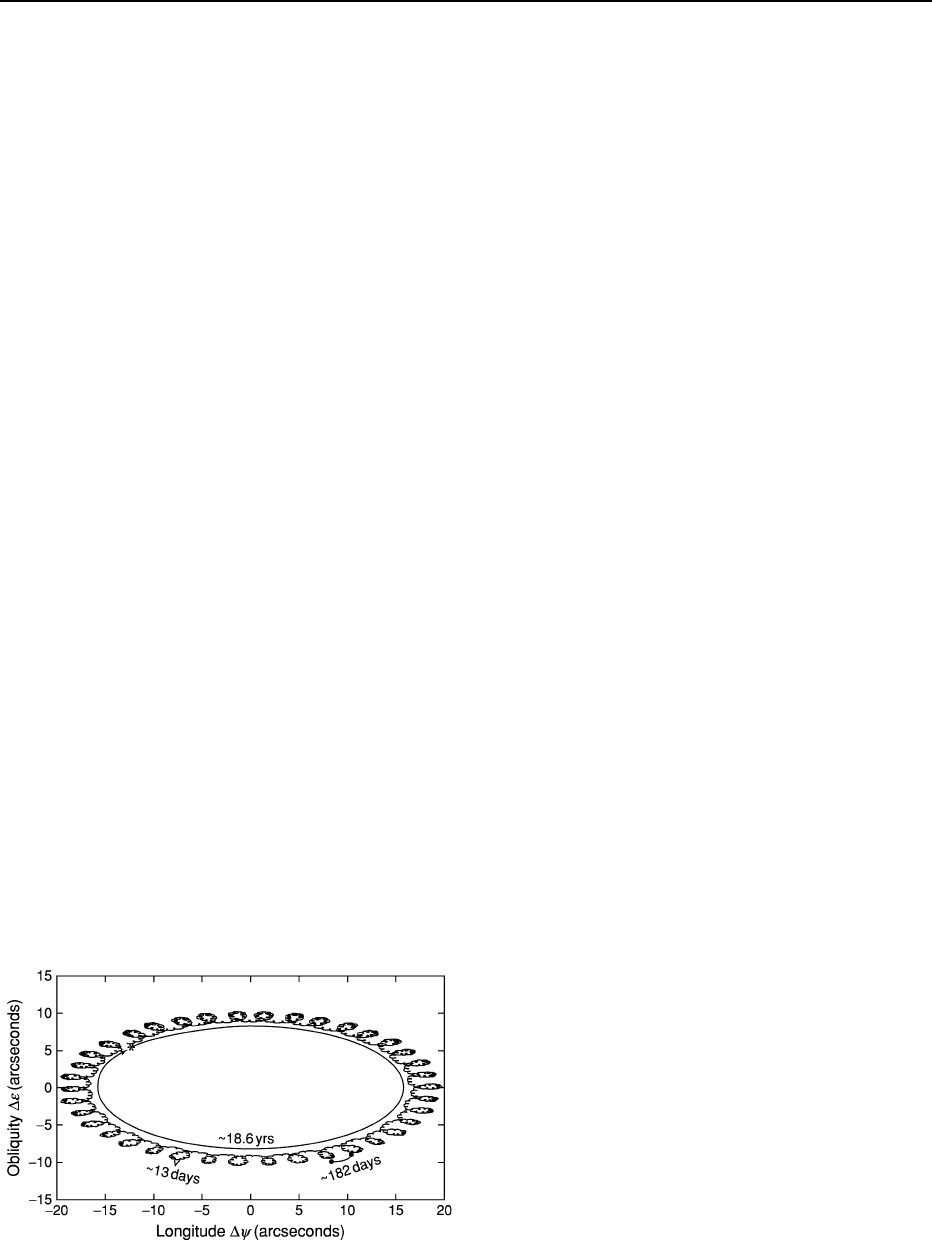
axis. Nutation is the short-term period portion

(periods 18.6 years) of these variations; precession

is the long-period portion. The nutational component

leads to a ‘nodding’ motion of Earth’s spin axis, with

main periods of 13 days, 6 months, 1 year, 9.3 years,

and 18.6 years, whereas the precessional component

makes Earth’s spin axis trace out a cone shape. The

short-term nutation component that is superimposed

on top of the longer term precession component is

illustrated in Figure 2, and the precession component

is illustrated in Figures 1 and 3. From a climatic per-

spective on geological time-scales, only the preces-

sion component has a significant effect; nutational

variations result in small, mainly atmospheric effects.

With respect to the fixed stars, the frequency p of

the precessional cycle has a period of approximately

25.8 ky. The precession of Earth’s spin axis has sev-

eral effects on Earth’s climate system, one of which is

that the position of the seasons with respect to Earth’s

orbit, defined by the solstices and equinoxes with

respect to the perihelion and aphelion of the orbit,

changes over time. For this reason, the precession of

Earth’s spin axis is also called the ‘precession of the

equinoxes’. As shown in Figure 1, the precession of

Earth’s spin axis traces out a cone shape that forms an

angle with Earth’s orbital plane. This angle, denoted

by e, is the obliquity (tilt) of Earth. The angle e

changes due to the combined effect of the precession

Figure 2 Short-term nutation motion of Earth’s spin axis, based

on nutation and precession model IAU2000A of the International

Astronomical Union. The nutation components in longitude and

obliquity are with respect to the equinox and ecliptic of date. The

figure is plotted for an 18.5-year period, beginning on 1 January

2004.

of Earth’s spin axis and the changing orientation of

Earth’s orbital plane (this will be discussed in more

detail in a following section).

As an approximation, the fundamental frequencies

and s

can be used together with the precession

constant p to explain the origin of almost all periodi-

cities that affect the climate system, which arise from

‘beats’ between the fundamental frequencies. How-

ever, Jacques Laskar discovered that additional reson-

ance terms are present in the Solar System, and these

lead to the presence of chaos. The presence of chaos

in the solar system has important consequences (see

later). How the three orbital parameters, eccentricity,

obliquity, and climatic precession, which are involved

in the calculation of the solar radiation, are related to

the fundamental frequencies of the Solar System is

discussed in the following sections. The main param-

eters, known as ‘Milankovitch cycles’, are illustrated

in Figure 3.

Eccentricity

Earth’s orbital eccentricity e quantifies the deviation

of Earth’s orbital path from the shape of a circle. It is

the only orbital parameter that controls the total

amount of solar radiation received by Earth, averaged

over the course of 1 year. The present eccentricity of

Earth is e  0.01671. In the past, it has varied be-

tween 0 and 0.06. The eccentricity value can be

used to compute the difference in the distance from

Earth to the Sun between their closest and furthest

approaches (perihelion and aphelion); presently, this

amounts to 2e  3.3%. At maximum eccentricity, the

annual variation of solar insolation due to eccentri-

city is thus 24%. Although the exact values of orbital

parameters should be computed by numerical inte-

gration, it is possible to approximate the calculation

as a series of quasiperiodic terms, some of which are

listed in Table 2. It is important to point out that the

eccentricity frequencies are completely independent

of the precession frequency p. Earth’s eccentricity

frequency component with the largest amplitude has

a period of approximately 400 ky, which arises mainly

from the interactions of the planets Venus and Jupiter,

due to their close approach and large mass, respect-

ively. This component is called the ‘long’ eccentricity

cycle, and of all of Earth’s orbital frequencies, it is

considered to be the most stable. Additional terms

can be found with periods clustered around 96

and 127 ky. These are called ‘short’ eccentricity

cycles.

An important feature of all orbital components is

the presence of ‘beats’. These arise from the inter-

action between different frequency components and

they produce a modulation in amplitude. This results,

for example, in an amplitude modulation of the short

eccentricity cycle, because the difference between the

412 EARTH/Orbital Variation (Including Milankovitch Cycles)

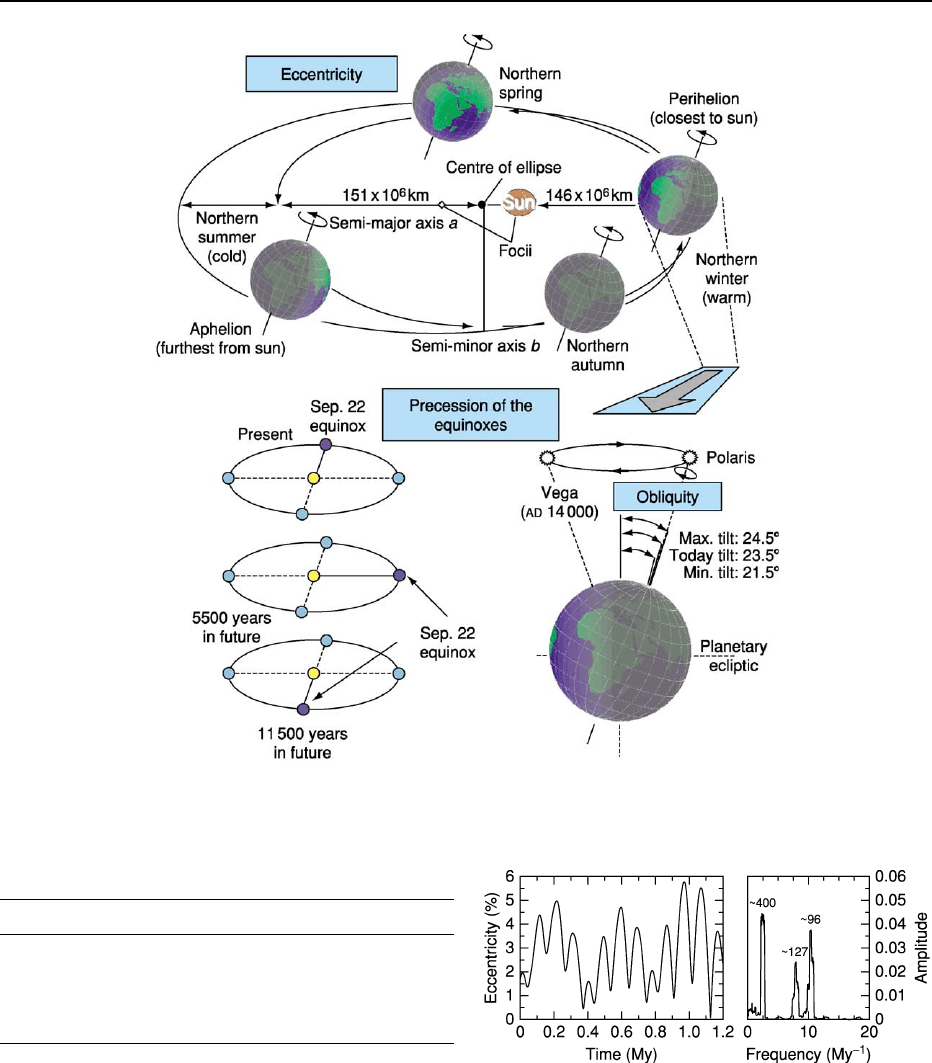
second and third strongest eccentricity components is

 g

)  (g

 g

) ¼ (g

 g

), which corresponds to

the 400-ky eccentricity cycle. The same modulation

is observed for the fourth and fifth strongest terms.

This type of amplitude modulation can be found in

all orbital components of Earth. The nature of

eccentricity variations is illustrated in Figure 4. The

superposition of the long and short eccentricity

cycles, and their variation in amplitude, are clearly

visible. The right-hand side of the plot shows the

Table 2 Five leading terms for Earth’s eccentricity

Term Frequency (

year

1

) Period (ky) Amplitude

 g

3.1996 406.182 0.0109

 g

13.6665 94.830 0.0092

 g

10.4615 123.882 0.0071

 g

13.1430 98.607 0.0059

 g

9.9677 130.019 0.0053

Principal eccentricity frequency components in an astronomical

solution analysed over the past 4 My. The frequency terms g

refer to those given in Table 1.

Data from Laskar J (1999) The limits of Earth orbital calculations

for geological time-scale use. Philosophical Transactions of the

Royal Society of London

, Series A, Mathematical, Physical and

Engineering Sciences

357(1757): 1735–1759.

Figure 3 Orbital motions of Earth, showing the main Earth orbital parameters, eccentricity, obliquity, and precession of the

equinoxes.

Figure 4 Earth’s orbital eccentricity over time (1.2 million

years) and frequency analysis for a 10-My time-span. The peaks

in the frequency analysis correspond to the frequencies given in

Table 2; the numbers over the peaks represent the periods

(in thousands of years).

EARTH/Orbital Variation (Including Milankovitch Cycles) 413

Elsevier Encyclopedia of Geology - vol I A-E

Подождите немного. Документ загружается.