Ellis A.M., Feher M., Wright T. Electronic and Photoelectron Spectroscopy: Fundamentals and Case Studies

Подождите немного. Документ загружается.

15 Photoelectron spectrum of NO

−

135

90°

180°

ONO

3σ

2σ

4σ

3σ

5σ

4σ

−

...

−

− −

−

Figure 15.3 Walsh diagram for the valence molecular orbitals of an XY

molecule such as NO

Approximate atomic orbital contributions to the MOs are shown. Notice that for the π MOs on the

right-hand side only the in-plane component is shown. Also, all σ

g/u

orbitals should actually be labelled

g/u

but the + superscript has been omitted for clarity.

Although we know NO

is bent, it is simpler to start by considering a linear geometry.

The valence MOs can be divided into two groups, σ and π orbitals. It is easy to envisage

that the energies of the σ MOs, in which the electron density points primarily along bonds,

will not be strongly altered if the molecule bends. Consequently, while the σ MOs will play

a major role in the N

O bonding, they do not have a strong inﬂuence on the equilibrium

bond angle.

The π orbitals in the linear molecule are doubly degenerate MOs. There are three sep-

arate π orbitals resulting from 2p orbital overlap, one bonding, one non-bonding, and one

antibonding. The right-hand side of Figure 15.3 shows the phases of the atomic orbitals for

the three π orbitals. As expected, in the bonding MO (1π

) all three atoms have 2p orbitals

with the same phase. In the antibonding MO (2π

) the 2p orbitals on the O atoms have the

same phase but opposite to that on the central N atom. In the non-bonding MO (1π

) the

136 Case Studies

O atoms have opposite phases and are therefore unable to interact with a 2pπ orbital on

nitrogen.

As the molecule bends, each π orbital loses its degeneracy and two distinct MOs are

formed with different symmetries. As shown in Figure 15.3,the1π

bonding MO is resolved

into a

and b

MOs.

The energies of these orbitals are not very sensitive to the bond angle

because the bonding interactions are largely unaltered by the bending process.

The π

non-bonding MO is resolved into a

and b

MOs when the molecule is bent. The

energies of both of these orbitals rise as the molecule bends due to increased antibonding

interactions between the O 2p orbitals. This is more pronounced for the b

component

because of the in-plane orientation of the O 2p orbitals, as can be seen from the AO

contributions shown on the left-hand side of Figure 15.3.

The antibonding 2π

MO of linear NO

is resolved into a

and b

orbitals when the

molecule is bent. The energy of the b

orbital is relatively insensitive to the bond angle.

However, the energy of the a

orbital is lowered dramatically as the molecule is bent. At ﬁrst

sight this might seem implausible; after all, the antibonding interactions between adjacent 2p

orbitals would not appear to be removed by bending the molecule. However, there is another

factor that needs to be taken into account, and which is not shown in Figure 15.3, namely

the mixing-in of nitrogen 2s character. Such mixing is strictly forbidden by symmetry at the

linear geometry (the 2s orbital on N has σ

symmetry and so cannot interact with the π

combination of 2p orbitals) but when the molecule bends mixing becomes possible (since

the 2s orbital on N now has a

symmetry and can interact with the a

component correlating

with the π

orbital). This mixing, or hybridization of the 2s and 2p orbitals on N, reduces

the antibonding interactions.

The above considerations are distilled into the diagram in Figure 15.3,which shows the

effect of the bond angle on molecular orbital energies. Such a diagram is known as a Walsh

diagram. Walsh diagrams are often used to provide a qualitative explanation of bond angles

in small molecules [7].

Seventeen electrons must be distributed amongst the twelve valence molecular orbitals

of NO

.Ifthe molecule is linear in its ground electronic state then these electrons will ﬁll

all orbitals up to and including 1π

. The remaining electron will be in the 2π

orbital, the

HOMO, which is the π antibonding orbital discussed earlier. Evidently, there will be some

energetic gain by bending the molecule so that the unpaired electron is now in the 6a

(which correlates with 2π

in the linear molecule limit). However, the energies of the 4b

and 1a

orbitals, both of which are doubly occupied, rise as the molecule is bent. Clearly

there will be a compromise and the equilibrium bond angle will adopt an intermediate value

between the linear and fully bent (90

◦

) limits. The known bond angle is 134

◦

, consistent

with this proposition.

This follows also from formal symmetry arguments. The combination of 2pπ orbitals on the O atoms with opposite

phases gives a symmetry orbital having π

symmetry. This cannot interact with a 2pπ orbital on the N atom since

all 2p orbitals on the central atom have u symmetry (because the phases on their two lobes have opposite signs). The

N2p orbitals therefore make no contribution to the π

antibonding MO.

When NO

is bent the symmetry is lowered from D

∞

to C

. The resulting symmetry of each orbital can be

deduced by consulting the C

character table and noting how the orbital is transformed under each symmetry

operation of the point group.

15 Photoelectron spectrum of NO

−

137

The additional electron in the ground electronic state of NO

−

will reside in the 6a

MO. Since this orbital will now be doubly occupied, the Walsh diagram leads us to expect

a smaller bond angle for NO

−

than NO

. These arguments conﬁrm the sign of the bond

angle change deduced by Erwin et al., namely that the bond angle increases by c.16

◦

photodetaching an electron from NO

−

References

1. K. M. Ervin , J. Ho, and W. C. Lineberger, J. Phys. Chem. 92 (1988) 5405.

2. Y. Morino, M. Tanimoto, S. Saito, E. Hirota, R. Awata, and T. Tanaka, J. Mol. Spectrosc.

98 (1983) 331.

3. W. J. Lafferty and R. L. Sams, J. Mol. Spectrosc. 66 (1977) 478.

4. M. W. Chase, C. A. Davies, J. R. Downey, D. J. Frurip, R. A. McDonald, and A. N. Syverud,

JANAF Thermochemical Tables, 3rd edn., J. Phys. Chem. Ref. Data, Suppl. 14 (1987).

5. Atomic Energy Levels,C.E.Moore, National Bureau of Standards, Circ. 467, Washington

DC, US Department of Commerce, 1949.

6. H. Hotop and W. C. Lineberger, J. Phys. Chem. Ref. Data 14 (1985) 731.

7. A. D. Walsh, J. Chem. Soc. (1953) 2260; ibid. (1953) 2266.

These arguments can also be extended to explain the change in bond length on photodetachment, although a more

sophisticated analysis is needed. See Reference [1] for further details.

Laser-induced ﬂuorescence

spectroscopy of C

: rotational

structure in the 300 nm system

Concepts illustrated: laser-induced ﬂuorescence spectroscopy; symmetries of electronic

states; assignment of rotational structure in spectra of linear molecules; combination

differences; band heads; nuclear spin statistics.

As described in Chapter 11, laser-induced ﬂuorescence (LIF) spectroscopy is one of the

simplest and yet most powerful tools for obtaining high resolution spectra. Its high sensitivity

is particularly convenient for the investigation of extremely reactive molecules, such as free

radicals and ions. In this Case Study we illustrate how LIF spectroscopy can be used to obtain

important information on a small carbon cluster, the C

molecule. The spectra presented

were originally obtained by Rohlﬁng [1], who produced C

by pulsed laser ablation of

graphite. This is a violent method for vaporizing a solid and the plasma formed above the

graphite surface will undoubtedly contain carbon atoms, clusters such as C

, and various

cations and anions. To reduce spectral congestion, the laser ablation source was combined

with a supersonic nozzle to produce a cooled sample for spectroscopic probing.

The LIF spectrum was obtained by crossing the supersonic jet with a tunable pulsed

laser beam and measuring the intensity of ﬂuorescence as a function of laser wavelength.

As discussed in Section 11.2,anLIF excitation spectrum is similar to an absorption spec-

trum but the signal intensity depends not only on the absorption probability, but also the

ﬂuorescence quantum yield of the upper state. C

has LIF spectra in several regions of the

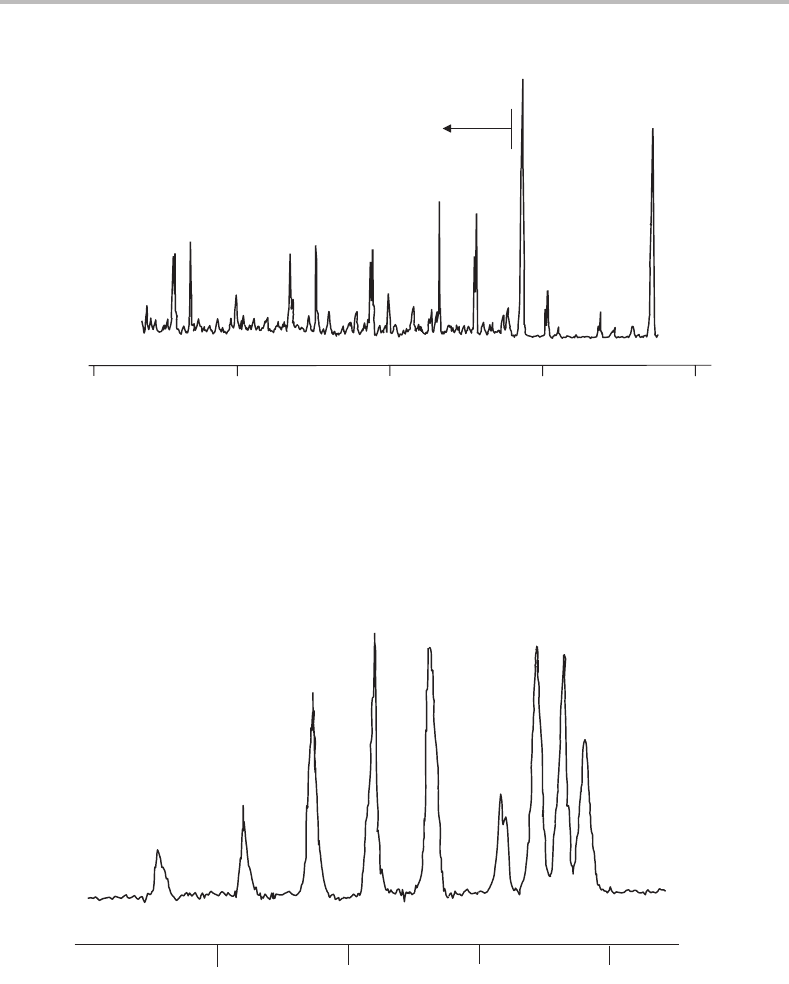
ultraviolet, and one such system, in the 298–311 nm region, is shown in Figure 16.1.Given

that this spectrum spans several hundred cm

−1

, most if not all of the coarse structure must

be vibrational in origin. Rotationally resolved scans of individual vibrational components

would greatly facilitate the spectral assignment, as well as providing structural information

on the molecule. Figure 16.2 shows a higher resolution scan of the strongest band in Figure

16.1, and this will now be considered in some detail.

16.1 Electronic structure and selection rules

Spectra of C

in the region shown in Figure 16.1 are very strong. Consequently, the transi-

tions presumably originate from the ground electronic state. Ab initio electronic structure

138

16 Laser-induced ﬂuorescence spectroscopy of C

139

32000

32400

32800

33600

Wavenumber/cm

−1

× 10

33200

Figure 16.1 Survey LIF excitation spectrum of jet cooled C

in the 32 145–33 500 cm

−1

region. The

band marked with an asterisk is rotationally resolved in Figure 16.2. (Reproduced with permission

from E. A. Rohlﬁng, J. Chem. Phys. 91 (1989) 4531, American Institute of Physics.)

−10

R(0)

R(2)

R(4)

R(6)

P(2)

P(4)

P(6)

P(8)

P(10)

−5

Relative wavenumber/cm

−1

Figure 16.2 Rotationally resolved LIF excitation spectrum of the vibronic band of jet-cooled C

33 147 cm

−1

. (Reproduced with permission from E. A. Rohlﬁng, J. Chem. Phys. 91 (1989) 4531,

American Institute of Physics.)

140 Case Studies

calculations on C

provide a useful starting point for understanding the electronic spectra.

is a linear molecule with an outer electronic conﬁguration...4σ

3σ

1π

,which gives

rise to a



ground electronic state. The highest occupied molecular orbital (HOMO),

the 1π

orbital, is a strongly bonding molecular orbital produced by the in-phase overlap

of C 2pπ atomic orbitals. The lowest unoccupied molecular orbital (LUMO) is the 1π

non-bonding MO formed by the 2pπ orbitals on the two carbon atoms at the ends of the

molecule having opposite phases. Since this orbital is vacant, electron promotion into this

orbital is possible. Only singlet states need be considered given the S = 0 spin selection

rule in electronic transitions. One-electron transitions from the 4σ

and 3σ

orbitals to the

LUMO yield



and



states, respectively, while the one-electron transition 1π

← 1π

gives three possible excited states,





, and



−

states.

Can the spectra be used to

distinguish between these possible transitions?

Rotational structure can provide important information on the symmetries of the upper

and lower states in a transition. In fact C

represents a relatively simple example where this

is true. Even without any detailed analysis it is clear from the spectrum in Figure 16.2 that

there are two distinct branches, which are easily identiﬁed as P(J =−1) and R(J =+1)

branches. There is no trace of any Q branch (J = 0), which shows that the transition must

be − in character, since any other possibility would give rise to a Q branch. Since ab

initio calculations show that the ground state is a



state, then the excited state must be



state. This follows from the application of symmetry arguments, which show that

electric dipole allowed transitions must satisfy g ↔ u, +↔+, and −↔−selection rules

(see Section 7.2.1). It would seem therefore that the symmetry of the excited electronic state

has been established. However, there is a problem with this assignment because high quality

ab initio calculations predict that the lowest



electronic state is ∼8eV(64500 cm

−1

)

above the ground electronic state, whereas the lowest



and



states are calculated to

be at about the right energy, 4.13 eV (33 313 cm

−1

) and 4.17 eV (33 635 cm

−1

), above the

ground state [2]. Although accurate prediction of the energies of electronic excited states is

sometimes difﬁcult to achieve through ab initio calculations, an error of several eV can be

ruled out for a high-level calculation. Consequently, the assignment based on the rotational

structure seems to be at odds with the ﬁndings of the ab initio calculations.

The explanation for this discrepancy lies in a breakdown of the Born–Oppenheimer

approximation. So far the selection rules have been stated for pure electronic transitions,

i.e. it has been assumed that the electronic and vibrational motions can be fully separated.

However, this separation is never exact, and in some cases the mixing is sufﬁciently large

that it is more appropriate to think in terms of a combined vibronic state, i.e. a mixed

vibrational–electronic state. In these circumstances the selection rules are determined by

the symmetries of the vibronic state(s), each of which is a combination of the symmetries

of the component vibrational and electronic symmetries. This breakdown of the Born–

Oppenheimer approximation is possible in polyatomic molecules by a mechanism known

These excited states can be established from direct products of the symmetries of the MOs, as described in Section

4.2.3. For example, the vacancy introduced into the 1π

MO as a result of the transition 1π

← 1π

yields

electronic states with spatial symmetries derived from π

⊗ π

= σ

+ σ

−

+ δ

.Incontrast to MOs, the

convention with electronic states is to employ upper case symmetry labels.

16 Laser-induced ﬂuorescence spectroscopy of C

141

as Herzberg–Teller coupling, sometimes also known as vibronic coupling (for more details

about Herzberg–Teller coupling see Case Study 25). In C

, there are three vibrational

normal modes, the symmetric stretch, the antisymmetric stretch, and the bending mode, with

, σ

, and π

symmetries, respectively.

The symmetries of the resulting vibronic states

can be determined from the direct product of the symmetries of the pure electronic and

pure vibrational states. If only the stretches are excited, then mixing of either the



or the



electronic state with any stretching vibrational state can never yield the required



vibronic state symmetry.

On the other hand, if there is one quantum in the bending mode when the molecule

is in the



electronic state, then three vibronic states,



−



, and



states, are

possible (as seen by taking the direct product



× π

). If the symmetries of vibronic

states for higher excitation of the bend are calculated it is readily shown that a



state is

produced on exciting odd quanta of the bending mode. Similarly even quantum excitation

of the bending mode within the



electronic state can also produce a



vibronic state.

Unfortunately, the data are insufﬁcient to be able to determine whether it is a transition to

the





electronic state that is being vibronically induced. However, we can at least

show that there is no inconsistency between the ab initio predictions and the spectroscopic

ﬁndings.

16.2 Assignment and analysis of the rotational structure

The rotational structure in Figure 16.2 appears to be very simple and indeed it is. The P

and R branches have already been pointed out, and clearly lines in the P branch diverge

away from the band centre whereas lines in the R branch converge. Our ﬁrst concern is to

extract the rotational constants for the upper and lower states from the spectrum. However,

before this is done it is beneﬁcial to derive an estimate of the rotational constant. Assuming

is linear and symmetrical (D

∞h

point group), the moment of inertia is I = 2m

where r is the C

C separation. Since we are not after an exact value at this stage, a

typical C

C bond length (1.3 Å) can be used to estimate the rotational constant, yielding

B ≈ 0.4 cm

−1

The interesting thing about the spectrum in Figure 16.2 is that all the lines have been

assigned to transitions out of levels with even J. The estimate of the rotational constant

allows us to show that this is correct. Accepting the assignment for the moment, the rota-

tional constants in the upper and lower electronic states can be assigned by the method of

combination differences, in which lines are identiﬁed that originate from, or terminate in,

a common rotational level. For example, both the R(J − 1) and P(J + 1) lines transitions

terminate at the Jth rotational level in the upper electronic state and hence the difference

R(J − 1) − P(J + 1) gives the energy difference between the (J + 1) and (J − 1) levels in

the lower electronic state. In a similar way, R(J) − P(J)gives the energy difference between

It is customary to employ lower case symbols to represent the normal coordinates of individual vibrations, as it is

to represent individual molecular orbitals. Upper case symbols are used for symmetries of overall electronic and

vibrational states.

142 Case Studies

Table 16.1 Approximate line positions and combination differences in

the LIF spectrum of the C

molecule

JP(J) R(J)

R(J − 1) − P(J + 1)

J + 1/2

R(J ) − P(J )

J + 1/2

033147.8

1.7333

233145.2 33 149.1 1.5600

1.7429

433143.0 33 150.1 1.5778

1.7636

633140.4 33 150.9 1.6154

1.7733

833137.6

10 33 134.6

the (J + 1) and (J − 1) levels in the upper state, because both transitions originate from the

same lower state level. Consequently, these two combination differences are given by





(J ) = R(J − 1) − P(J + 1) = B



(J + 1)(J + 2) − B



(J − 1)J

= 4B





J +







(J ) = R(J ) − P(J ) = B



(J + 1)(J + 2) − B



(J − 1)J

= 4B





J +



in the rigid rotor limit, where the



and



labels refer to quantities in the upper and lower states,

respectively. The observed lines and the combination differences are given in Table 16.1.

As can be seen, the combination differences, when divided by J +

,giveanearly constant

value, as expected from the relationships above; the slow increase is due to the neglect of

centrifugal distortion, which is normally very small at low J.

The rotational constants in the lower and upper states can be derived from the intercept

of a line ﬁtted through these points by linear regression. As the intercepts equal 4B



and



, the rotational constants are B



= 0.438 ± 0.005 and B



= 0.396 ± 0.007 cm

−1

. The

corresponding C

C bond lengths are therefore 1.263 ± 0.007 Å and 1.328 ± 0.012 Å,

respectively. The increase in bond length on electronic excitation is consistent with the idea

of an electron moving from a bonding MO to a non-bonding MO.

The rotational constants extracted from the spectral analysis are reasonably close to

our earlier estimate. If the assignments in Figure 16.2 were wrong, and instead the P

and R branch lines with odd rotational quantum numbers were not missing, then rotational

constants roughly twice as large as the above values would be obtained. This would clearly be

physically unreasonable, and we would have to conclude that the assignment was incorrect.

The absence of lines from odd J levels is the result of nuclear spin statistics, which is

important in molecules where two or more atoms are in equivalent locations. C

is a good

example since the terminal carbon atoms are equivalent; other examples would include C

O, and NH

. Interested readers can ﬁnd a brief discussion on the origin of nuclear

spin statistics and its impact on the rotational levels of molecules in Appendix F. The effect

16 Laser-induced ﬂuorescence spectroscopy of C

143

for C

is that, because the nuclear spin of the most abundant isotope,

C, is I = 0, only

even J levels exist in the



ground state and odd J levels in the excited vibronic



state. As a result every second line is missing from the spectrum.

16.3 Band head formation

The convergence of the R branch and divergence of the P branch is a consequence of the

difference in rotational constants between the upper and lower states. To see how this arises,

consider the expression for the position of R branch transitions:

ν(R(J )) = F



(J + 1) − F



(J ) = ν

+ B



(J + 1)(J + 2) − B



J (J + 1)

= v

+ 2B



+ (3B



− B



)J + (B



− B



In the above expression ν

represents the transition frequency in the absence of rotational

structure. If B



and B



differ then the quadratic term in J may be signiﬁcant, particularly

at high J.IfB



> B



then ν(R(J )) will reach a maximum at some value of J and begin to

decrease as J continues to increase, i.e. the branch forms a so-called band head.Beyond the

band head the branch reverses direction and diverges as J continues to increase. In contrast,

the P branch will simply diverge as J increases. This is clearly the behaviour observed for

the spectrum of C

in Figure 16.2.IfB



> B



it is the P branch that has a band head and the

R branch that diverges.

Band heads are not always observed if |B



−B



| is very small, since the turning point

occurs for transitions out of a high rotational level and this may have an insigniﬁcant

population at the given temperature. Clearly band head formation is an indicator of the sign

and magnitude of the difference B



−B



The band head in the C

spectrum occurs at R(6);

higher R branch transitions are hidden under the stronger (low J ) R branch transitions.

References

1. E. A. Rohlﬁng, J. Chem. Phys. 91 (1989) 4531.

2. J. R ¨omelt, S. D. Peyerimhoff, and R. J. Bunker, Chem. Phys. Lett. 58 (1978) 1.

Even if the rotational structure is not fully or even partially resolved, the shape, or contour,ofthe band still

provides information on the rotational constants. Even if no individual peaks were resolved in a low resolution

version of Figure 17.2, the overall band would clearly be asymmetric with a tail on the long wavelength side. Such

a band is referred to as being red-shaded, and this red-shading immediately reveals that B



< B



Photoionization spectrum

of diphenylamine: an unusual

illustration of the

Franck–Condon principle

Concepts illustrated: MATI spectroscopy; vibrational wavefunctions; Franck–Condon

principle and Franck–Condon factors.

The photoionization spectrum of diphenylamine provides an unusual and interesting illus-

tration of the Franck–Condon principle. Diphenylamine (DPA), illustrated in Figure 17.1,is

a relatively large molecule to study by gas phase spectroscopy and it might be thought that

the vibrational structure in its electronic spectra would be highly congested and difﬁcult to

interpret. After all, this is a molecule with 66 vibrational modes! However, it was shown in

Section 7.2.3 that only totally symmetric modes generally need to be considered in inter-

preting electronic spectra. Also, there is the further simpliﬁcation that not all of the totally

symmetric modes need be Franck–Condon active, i.e. will give a signiﬁcant progression.

DPA is an excellent example of this, with the main structure arising from a single vibrational

mode.

Before spectra are considered, the experimental procedure, carried out by Boogaarts and

co-workers [1], will be outlined. Mass-analysed threshold ionization (MATI) spectroscopy

was employed. This technique, which was brieﬂy described in Section 12.6,isessentially

the same as ZEKE spectroscopy but employs ion rather than electron detection. It has

the advantage over ZEKE spectroscopy in that ions can be separated according to their

mass, which in most cases enables the spectral carrier to be determined with conﬁdence.

By analogy with ZEKE spectroscopy, a cation ← neutral molecule electronic absorption

spectrum is effectively obtained.

In the experiments on DPA this molecule was promoted from its ground electronic state,

which is a spin singlet (S

), to its ﬁrst excited singlet state (S

), using the output from a

pulsed dye laser. Different vibrational levels of the S

state can be accessed by appropriate

choice of the dye laser wavelength, λ

.Apulse from a second dye laser was then employed

to ionize DPA from its S

state, with the ion signal being detected as a function of the

wavelength, λ

,ofthis dye laser. Actually the experiment is a little more complicated in

that only threshold ions are detected, i.e. those ions for which the corresponding electron

144