Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.12. Линейное программирование

413

Проиаводство

"Pink Flu",

л/день ,

Специальный ингредиент

0,01р +

0,04т

" 16 кг /день

А - точка, в которой достигается

моксимольиый доход

Типичный доход

0,1р+0,3т-

-ЮОф.ст./день

Время работы оборудовония

0,02р

+ 0,4т - 24 ч /день

^УУУУУУУУ^УЛ

Производство

"Mint Pop",

л/день

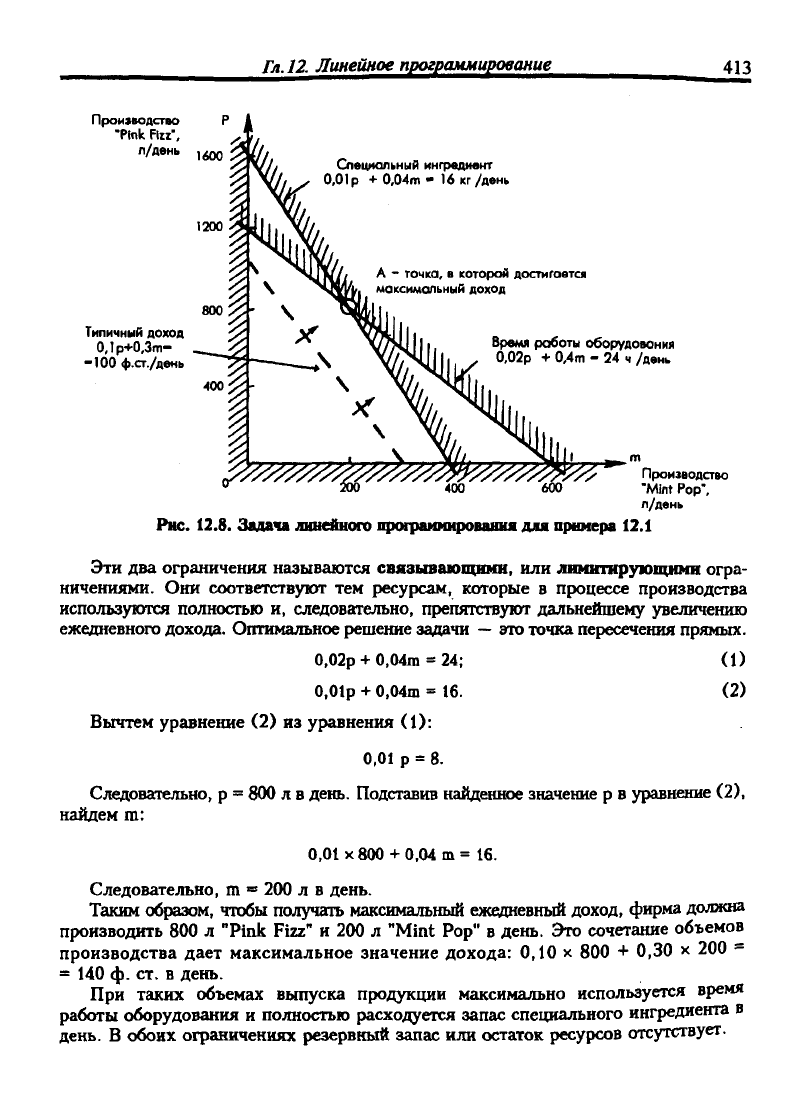
Рис. 12.8. Задача линейного профаимирования для примера 12.1

Эти два ограничения называются связывающими, или лимитирующими огра-

ничениями. Они соответствуют тем ресурсам, которые в процессе производства

используются полностью и, следовательно, препятствуют дальнейшему увеличению

ежедневного дохода. Оптимальное решение задачи — это точка пересечения прямых.

0,02р

0,04т

= 24; (1)

O.Olp

0,04m

= 16. (2)

Вычтем уравнение (2) из уравнения (1):

0,01 р = 8.

Следовательно, р = 800 л в день. Подставив найденное значение р в уравнение (2),

найдем ш:

0,01

800 +0,04 т= 16.

Следовательно, m •= 200 л в день.

Таким образом, чтобы получать максимальный ежедневный доход, фирма должна

производить 800 л "Pink Fizz" и 200 л "Mint Pop" в день. Это сочетание объемов

производства дает максимальное значение дохода: 0,10 х 800 + 0,30 х 200 =

= 140 ф. ст. в день.

При таких объемах выпуска продукции максимально используется время

работы оборудования и полностью расходуется запас специального ингредиента в

день.

В обоих ограничениях резервный запас или остаток ресурсов отсутствует.

414 Ч. 4.

Моделирование

в бизнесе

Этот метод определения оптимальной крайней точки зависит от того, насколько

правильно была построена линия уровня дохода. Ниже излагается практический

прием, который может помочь при нанесении на график линии уровня, которая

будет являться основой для определения оптимальной крайней точки. Выберем

любую удобную точку, лежащую приблизительно в середине допустимого множества.

Предположим, что в примере, изложенном выше, выбрана точка с координатами

р = 200, m = 200. Ежедневный доход от выпуска продукции в таком объеме

составит:

Р = 0,10 р + 0,30 m = 0,10

200 + 0,30 х 200 = 80 ф. ст. в день.

Все остальные сочетания объемов производства, позволяющие получать 80 ф. ст.

ежедневного дохода, принадлежат прямой

80 = 0,10 р + 0,30

(ф. ст. в день).

Одна точка этой прямой уже известна, это

—

точка с координатами р = 200,

m = 200. Для определения другой точки можно положить m = О, тогда р = 800.

Теперь мы можем построить на графике эту линию уровня ежедневного дохода и,

используя вышеизложенный алгоритм, определить оптимальное решение (или

решения). Очевидно, что в результате применения данного алгоритма оптимальное

решение всегда будет представлено либо крайней точкой множества, либо в случае,

если целевая функция параллельна одному из ограничений, множеством точек

отрезка, соединяющего две крайние точки.

Мы предполагали, что переменные в задаче линейного программирювания

непрерывны или, если это -условие не выполняется, могут принимать дробные

значения. И действительно, часто имеет место ситуация, когда в течение временного

п{юмежутка, рассматриваемого в задаче, допустимы дробные значения объемов

выпускаемой прюдукции. Если, например, производятся две модели автомобилей,

а цель задачи линейного программирования состоит в максимизации использования

оборудования в неделю, может оказаться, что оптимальное решение предполагает

наличие к концу недели незавершенного производства. При такой постановке

задачи, когда рассматриваемый период времени равен одной неделе, незавершенное

прюизводство вполне допустимо.

Если, однако, необходимо осуществить распределение рабочих по определенньп4

видам работ, дробные значения для числа рабочих недопустимы. Б этом случае

оптимальное решение должно включать только целые значения. Допустимыми

решениями $1вляются все точки допустимого множества, в которых переменные

принимают целые значения. В качестве оптимального решения выбирается последняя

точка допустимого множества, координаты которой являются целыми числами, однако

в данном случае она может уже не быть крайней точкой допустимого множества.

В задаче линейного программирования с двумя переменными процедура нахож-

дения оптимального решения в условиях целочисленности переменных не составляет

особого труда. Вместо допустимого множества рассматривается множество допус-

тимых точек, лежащих в пределах заданных ограничений. Движение типичной

линии уровня целевой функции осуществляется не вдоль всего допустимого

множества, а только через данные точки. Однако при решении задачи с множеством

Гл.

12.

Линейное программирование

415

переменных используется один из методов целочисленного программирования

рассмотрение которых выходит за рамки этой книги.

О Пример 12.S. Обратимся к примеру 12.2, в котором рассматривалось произ-

водство двух типов деталей к автомобилям. Необходимо определить о(5ъемы производ-

ства, при которых достигается максимальное значение общего дохода за неделю.

Решение.

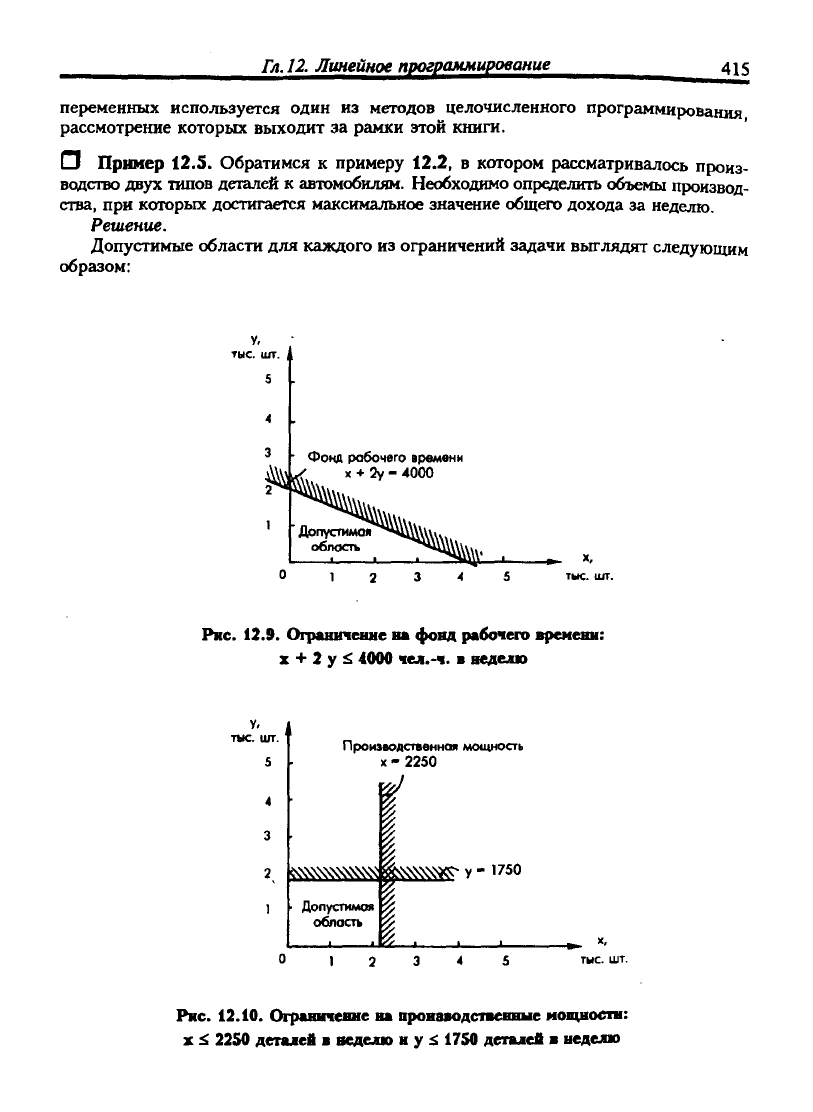
Допустимые области для каждого из ограничений задачи вьплядят следующим

образом:

тыс. UJT.

2*4

• Фона рабочего времени

^ X + 2у - 4000

' ДрпустиА«и1^*114Ши..

область

^^^*ш\\

Рис. 12.9. Огрантенне ва фонд рабочего времени:

х + 2 у £ 4000 чел.-ч.

веделю

у,

тыс.

МП.

Производстаенная мощность

X - 2250

»ч\\\\\\\\\\\Х

Долуспшсп

область

^^^^SS-Y- 1750

тыс. шт.

Ркс. 12.10. Ограннчевнс на пронаводетвевные иопцюстн:

^ 2250 деталей

веделю в у ^ 1750 деталей в неделю

416

Ч. 4. Моделирование в бизнесе

тыс. шт. ,,

Металлические стержни

2х + 5у- 10000

\ 2 3 А S тис. шт.

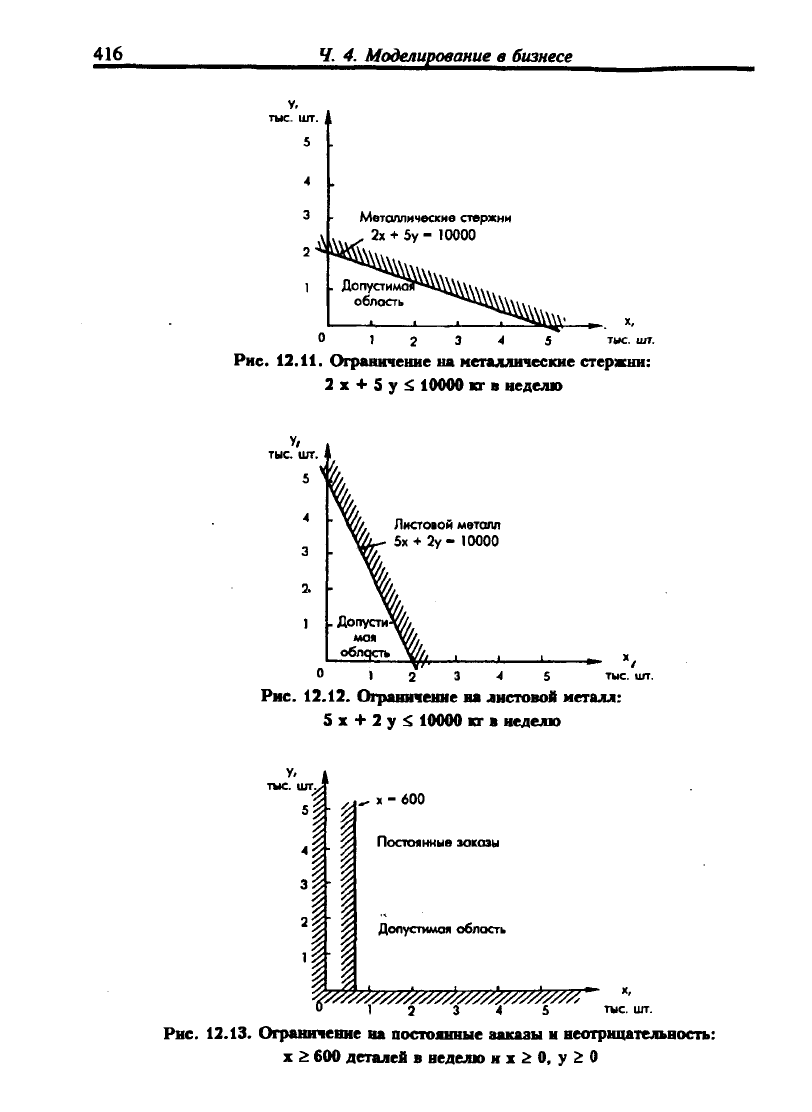
Рис.

12.11.

Ограничение на металлические стержни:

2 X + S у ^ 10000 кг в неделю

Листоаой металл

5х + 2у- 10000

О 12 3 4 5

Рис. 12.12. Ограшпение ва листовой металл:

S X + 2 у ^ 10000 кг в неделю

тыс. ил.

тыс. шт

'^ м-

- 600

^11

,^5;

^ Постоянные заказы

у у Долуспшая область

11.

о 12 3 4 5 тыс. шт.

Рнс. 12.13. Ограничение ва постоянные аакааы и неотрнцательность:

X i 600 деталей в неделю н х ^ О, у 2

Гл.12.

Линейное

программирование

417

тыс. шт.'

Профсоюзное соглошенив

+ у - 1500

%v Д°

Допустимая область

0^ VW'

тыс.

ия.

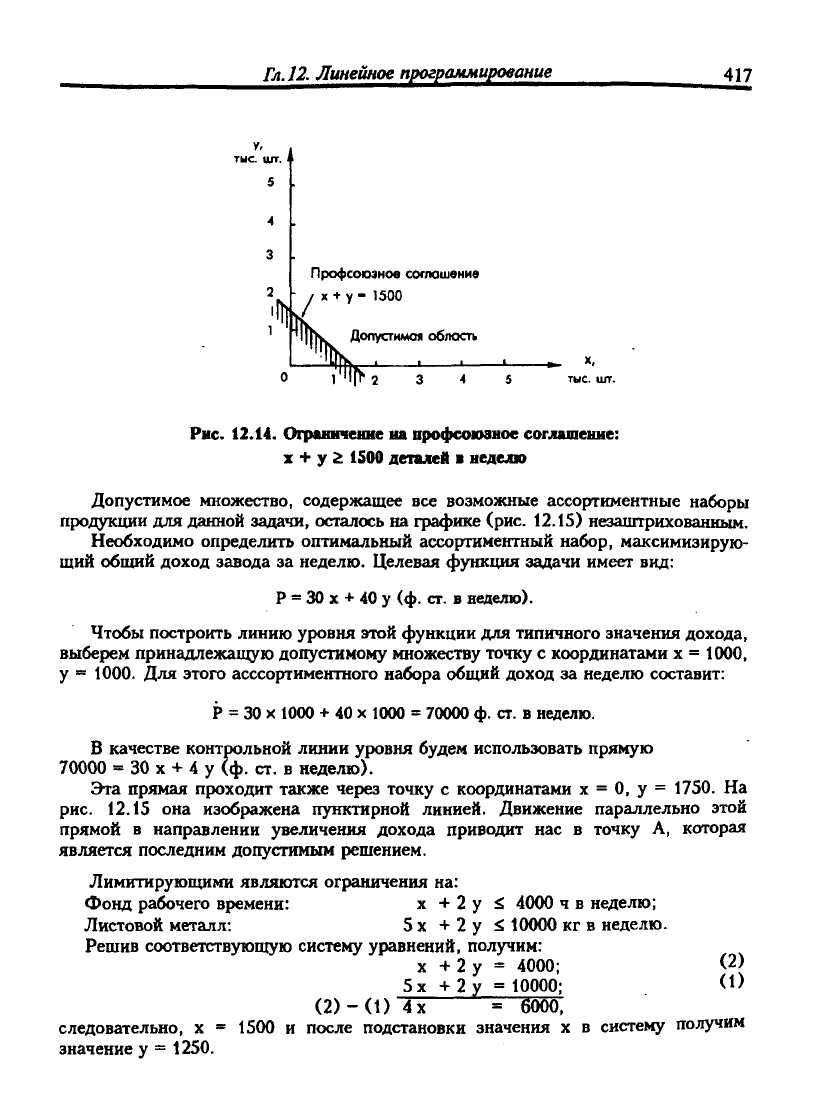
Рис.

12.14. Ограшпение на профсоюзное соглашение:

+ у 2 1500 деталей • неделю

Допустимое множество, содержащее все возможные ассортиментные наборы

продукции для данной задачи, осталось на графике (рис. 12.15) незаштрихованным.

Необходимо определить оптимальный ассортиментный набор, максимизирую-

щий общий доход завода за неделю. Целевая функция задачи имеет вид:

Р = 30

+ 40 у (ф. ст. в неделю).

Чтобы построить линию уровня этой функции для типичного значения дохода,

выберем принадлежащую допустимому множеству точку с координатами х = 1000,

у = 1000. Для этого асссортиментного набора общий доход за неделю составит:

Р = 30

1000 + 40

1000 = 70000 ф. ст. в неделю.

В качестве контрольной линии уровня будем использовать прямую

70000 = 30

+ 4 у (ф. ст. в неделю).

Эта прямая проходит также через точку с координатами х = О, у = 1750. На

рис.

12.15 она изображена пунктирной линией. Движение параллельно этой

прямой в направлении увеличения дохода приводит нас в точку А, которая

является последним допустимым решением.

Лимитирующими являются ограничения на:

Фонд рабочего времени: х + 2 у 5 4000 ч в неделю;

Листовой металл: 5 х + 2 у S 10000 кг в неделю.

Решив соответствующую систему уравнений, получим:

X +2у = 4000; (2)

+ 2 у = 10000; (1>

(2) - (1) Тк = 6000,

следовательно, х = 1500 и после подстановки значения х в систему получим

значение у = 1250.

418

Ч. 4. Моделирование в бизнесе

Выпуск деталей типа

V • недело,

тыс.

шт.

Листы

5х + 2у - 10000

\/ Заказы

г- х-600

Мощность

Точте • « - 2250

получения §

S манси- ^

Сотошенив

X+Y-I500

Типичмый доход,

30jci-40y-

-70000

Мощность

у.-

1750

Стержни 2х + 5у - 10000

Фонд аременн

-4000

Выпуск детолей

типа X • неделю,

тыс.

шт.

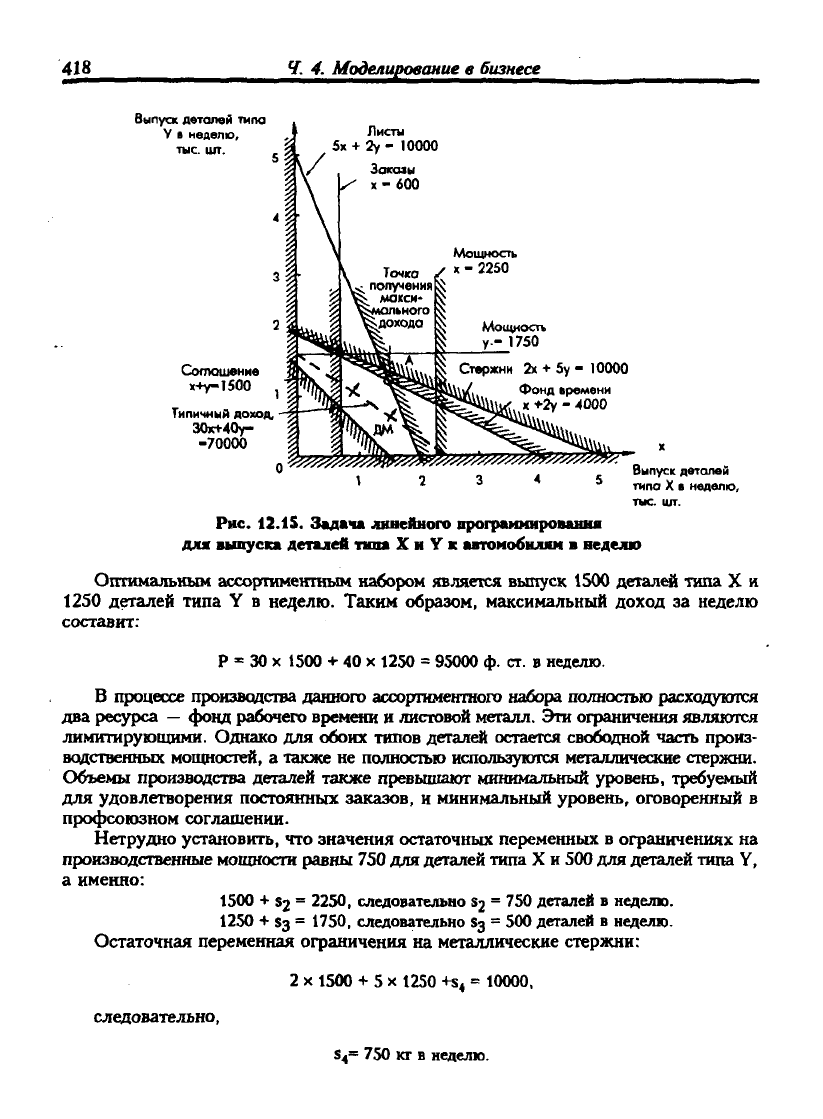
Рис. 12.1S. Задача линейного програимиромшия

для выпуска деталей mm X и Y к автоиобнляи в неделю

Оптимальным ассортиментным набором является выпуск 1500 деталей типа X и

1250 деталей типа Y в не;{елю. Таким образом, максимальный доход за неделю

составит:

Р = 30

1500 + 40

1250 = 95000 ф. ст. в неделю.

В прюцессе произвоаства данного ассортнментаого набора полностью расходуются

два ресурса — фонд рабочего времени и листовой металл. Эти ограничения являются

лимитирующими. Однако для обоих типов деталей остается свободной часть произ-

водственных мощностей, а также не полностью используются металлические стержни.

Объемы производства деталей также превышают минимальный уровень, требуемый

для удовлетворения постоянных заказов, и минимальный уровень, оговоренный в

профсоюзном соглашении.

Нетрудно установить, что значения остаточных переменных в ограничениях на

производственные мощности равны 750 для деталей типа X и 500 для деталей типа Y,

а именно:

1500 + $2 = 2250, следовательно

ъ^

~ 750 деталей в неделю.

1250 + S3 = 1750, следовательно S3 = 500 деталей в неделю.

Остаточная переменная ограничения на металлические стержни:

1500 + 5

1250 +S4 = 10000.

следовательно.

84= 750 кг в неделю.

Избыточная переменная ограничения на постоянные заказы:

1500

Sg =

600,

следовательно,

= 900 деталей в неделю

сверх минимального количества, необходимого для удовлетворения постоянных

заказов. Избыток по профсоюзному соглашению составил;

1500 +

1250

Sj=

1500,

следовательно,

1250

деталей в неделю

сверх минимального количества деталей, оговоренного в профсоюзном соглашении.

Как уже отмечалось выше, оптимальньш решением обычно является крайняя

точка допустимого множества. Следовательно, после построения графика определить

оптимальную крайнюю точку можно путем подсчета значений целевой функции во

всех крайних точках допустимого множества. Множество значений переменной,

соответствующей крайней точке допустимого множества, называется базисным

решением. Переменные, принимающие ненулевые значения в некоторой крайней

точке, называются базисными переменными.

Иногда в процессе решения задачи линейного программирования возникают

некоторые

трудности.

Задача может оказаться несовмеслюй.

В этом

случае допустимое

множество задачи является пустым. Ни одно сочетание переменных не удовлетворяет

всем ограничениям задачи одновременно и задача не имеет р>ешевий. Если в данной

ситуации все же необходимо найти решение задачи, чтобы построить допустимое

множество, то необходимо исключить одно или несколько ограничений.

Проблемы иного рода возникают, если задача линейного программирования

является неограниченной. В этом случае решение задачи может неограниченно

улучшаться, не нарушая при этом ни одного ограничения задачи. Обычно это

означает, что задача линейного программирования сформулирована некорректно,

и некоторые ограничения в ней отсутствуют.

О возможности существования целого множества оптимальных решений мы

уже говорили. Это случается, если целевая ф}гнкция параллельна лимитирующему

ограничению задачи. Оптимальное значение целевой функции будет достигаться в

любой точке этого ограничения, лежащей между двумя оптимальными крайними

точками, и соответственно любая из этих точек является оптимальным решением

модели. Эта ситуация имеет рад преимуществ, поскольку предоставляет админи-

страции некоторую свободу в принятии решений.

12.4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ

В большинстве случаев принятия решений полезно составить предварительный

план действий, чтобы проанализировать, какое воздействие окажут изменения,

вносимые в исходную задачу, на принятое решение. УЬшейное программирование не

420 Ч. 4. Моделирование в

бизнесе

является исключением. Существуют три аспекта решения задач линейного програм-

мирования, которые необходимо подвергнуть тщательному изучению:

• воздействие дополнительного количества лимитирующего ресурса;

• воздействие дополнительного количества нелимитирующих ресурсов;

• воздействие изменений в коэффициентах целевой функции. Рассмотрим

каждую из этих ситуаций в отдельности. При дальнейшем рассмотрении

примем предпосылку о том, что в любой момент времени изменяется только

один параметр.

12.4.1.

Воздействие изменений в обеспечении лимитирующим

ресурсом на решение задачи линейного профаммирования

Поскольку один или несколько ресурсов используются полностью, значение

целевой функции ограничено. Если появляется дополнительное количество лими-

тирующего ресурса, то оптимальное решение может быть улучшено. Однако

необходимо принять во внимание, что изменение оптимального решения приведет

к улучшению значения целевой функции только в том случае, если сумма допол-

нительных издержек по обеспечению дополнительным количеством ресурса не

превышает сумму прибыли, полученной в результате его использования.

С увеличением объема лимитирующего ресурса соответствующее ограничение

становится менее жестким. Так как жесткость лимитирующего ограничения посте-

пенно снижается, его график будет перемещаться параллельно своему начальному

положению, одновременно будет происходить перемещение оптимальной крайней

точки в направлении, которое улучшает значение целевой функции. Этот процесс

будет продолжаться до тех пор, пока какой-либо др)ггой {юсурс не будет полностью

использован и рассматриваемое ограничение перестанет бьггь лимитирующим.

Величина, на которзгю увеличивается значение целевой функции при снижении

жесткости лимитирующего ограничения на единицу, т.е. при увеличении количества

лимитирующего ресурса на единицу, называется теневой ценой ресурса. Теневая

цена ресурса

—

это стоимость единицы данного ftecypca в оптимальном решении.

Увеличение объема лимитирующего ресурса на единицу целесообразно только в

том случае, если существует возможность его получения по стоимости, которая

ниже, чем теневая цена данного ресурса.

О Пример 12.6. Обратимся к примерам 12.2 и 12.5. Из примера 12.S мы знаем,

что лимитирующими являются ограничения на фонд рабочего времени и на листовой

металл. Рассмотрим сначала последнее из указанных офаничений. Обратимся к

графику, изображенному на рис. 12.16. Жесткость ограничения на листовой

металл снижается по мере перемещения линии ограничения параллельно ее исходному

положению в противоположном направлении от начала координат. Допустимое

множество расширяется, а оптимальная крайняя точка пертмещается вниз по

линии ограничения на фонд рабочего времени, что увеличивает х и уменьшает у.

Снижение жесткости ограничения на листовой металл является эффективным до

тех пор, пока линия ограничения не достигнет точки пересечения ограничений на

фонд рабочего времени и производственные мощности для деталей типа X, т.е.

Гл.12.

Линейное

программирование

421

точки в. Если и далее снижать жесткость ограничения на листовой металл оно

перестанет быть лимитирующим, что приведет к появлению остатка в виде неис-

пользованного листового металла.

Выпуск деталей типа

У в неаелю.

Листы

5х + 2у- 10000

Новый оптимум при увеличении

фонда рабочего времени

х+у-1500

Исходный оптимум

'jf///,///у/////,/,,,„,

у - 1750

Новый оптимум при увеличении

листового металла

Стержни 2х + 5у - 10000

Фонд времени

X +2у - 4000

Выпуск деталей

типа X в неделю,

тыс. шт.

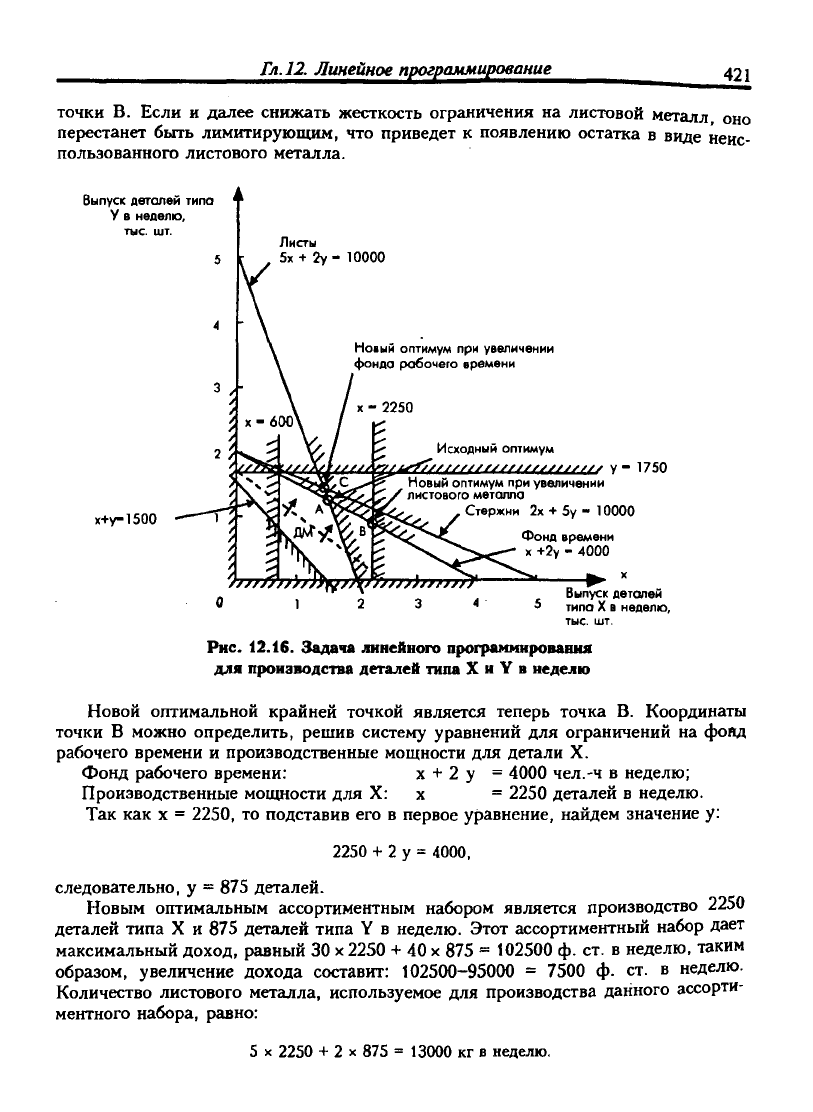
Рис.

12.16. Задача линейного программирования

для производства деталей типа X и Y в неделю

Новой оптимальной крайней точкой является теперь точка В. Координаты

точки В можно определить, решив систему уравнений для ограничений на фойд

рабочего времени и производственные мощности для детали X.

Фонд рабочего времени: х + 2 у = 4000 чел.-ч в неделю;

Производственные мощности для X: х = 2250 деталей в неделю.

Так как х = 2250, то подставив его в первое уравнение, найдем значение у:

2250 + 2 у = 4000,

следовательно, у = 875 деталей.

Новым оптимальным ассортиментным набором является производство 2250

деталей типа X и 875 деталей типа Y в неделю. Этот ассортиментный набор дает

максимальный доход, равный 30 х 2250 + 40 х 875 = 102500 ф. ст. в неделю, таким

образом, увеличение дохода составит: 102500-95000 = 7500 ф. ст. в неделю.

Количество листового металла, используемое для производства данного ассорти-

ментного набора, равно:

2250 + 2

875 = 13000 кг в неделю.

4.22 Ч. 4. Моделирование в бизнесе

Оно превышает начальное количество на 3000 кг в неделю. В новой оптимальной

точке фонд рабочего времени и производственные мощности для деталей X также

используются максимально.

Дополнительное количество листового металла

—

3000 кг

—

позволяет получать

дополнительный доход, равный 7500 ф. ст. в неделю, следовательно, теневая цена

данного ресурса составит: 7500 : 3000 = 2,50 ф. ст. за

кг. Каждый дополнительный

килограмм листового металла ведет к увеличению еженедельного дохода в 2,50 ф. ст.

Из этого следует, что сверхнормативный запас этого ресурса целесообразен только

в случае, если стоимость получения любого дополнительного количества ресурса

не превышает 2,50 ф. ст. за 1 кг ресурса.

Предположив, что ограничение на листовой металл остается неизменным,

применим аналогичную процедуру ко второму лимитирующему ограничению.

Если жесткость ограничения на фонд рабочего времени снизилась на единицу,

т.е.

появилась возможность использовать 1 чел.-ч рабочего времени дополнительно,

то тогда данное ограничение принимает вид:

х +

2у^4001.

Данное ограничение параллельно первоначальному, но его линия находится

дальше от начала координат по сравнению с исходной линией. Из приведенного

выше графика легко видеть, что точка пересечения ограничения на листовой

металл и нового ограничения на фонд рабочего времени все еще является опти-

мальной крайней точкой. В данном случае оптимальным решением является точка

с координатами х = 1499,75 и у = 1250,625, что приводит и к значению целевой

функции Р„ищ = 95017,50 ф. ст. Таким образом, значение целевой функции увеличи-

лось на 17,50 ф. ст. Теневая'цена фонда рабочего времени составляет 17,50 ф. ст. за

1 чел.-ч. Если можно получить один дополнительный час рабочего времени за

дополнительные 17,50 ф. ст. или менее, то это необходимо использовать. Если же

стоимость

чел.-ч. превьппает 17,50 ф. ст., то дополнительное количество рабочего

времени использовать нецелесообразно.

Какое количество дополнительного рабочего времени следует купить? По-

скольку линия ограничения на фонд рабочего времени движется параллельно своему

исходно»ог положению в направлении от начала координат, она стремится к точке

пересечения ограничений на листовой металл и металлические стержни к точке С.

Если и далее снижать жесткость ограничения на фонд рабочего времени, то оно

перестанет быть лимитирующим, и дальнейшее привлечение дополнительного

рабочего времени нецелесообразно. Максимальное число дополнительных чело-

веко-часов можно определить, решив систему ограничений, линии которых пере-

секаются в точке С:

Листовой металл: 5 х + 2 у = 10000;

Металлические стержни: 2 х + 5 у = 10000.

Ее решением являются следующие значения переменных:

= 10000/7 и у = 10000/7 деталей в неделю.

Число используемых в точке С человеко-часов равно:

+ у = 10000/7 + 2 (10000/7) = 4285,7 чел.-ч в неделю.

Это значение на 285,7 чел.-ч превосходит первоначальное максимальное значение

4000

чел.-ч.

Получение максимального сверхнормативного запаса

285,7 чел.-ч в неделю