Дзюбенко А.Л., Ильин А.А., Мишин П.Н. и др. Информационные технологии управления: Учебное пособие

Подождите немного. Документ загружается.

Теперь необходимо скопировать матрицу, обратную матрице коэф-

фициентов СЛАУ (ячейки (

B24:D26)) в ячейки (C28:E30), а вектор свобод-

ных членов СЛАУ (ячейки (

B14:D16)) в ячейки (I28:I30).

Алгоритм процедуры копирования представлен в табл. 1.

Табл. № 3.1

Алгоритм копирования матрицы, обратной матрице коэффициентов СЛАУ

и вектора свободных членов СЛАУ

№

п/п

Щелкнуть левой кнопкой мани-

пулятора “мышь” по ячейке

Набрать в строке формул … и

нажать Enter

Копировать матрицу

1−

(ячейки B24:D26)) в ячейки (C28:E30)

1. B24 =C28

2. B25 =C29

3. B26 =C30

4. C24 =D28

5. C25 =D29

6. C26 =D30

7. D24 =E28

8. D25 =E29

9. D26 =E30

Копировать вектор свободных членов СЛАУ B (ячейки B14:D16)) в ячейки

(

H28:H30)

1. B14 =G28

2. B15 =G29

3. B16 =G30

Процедура копирования позволяет при изменении исходных данных

СЛАУ (матрицы коэффициентов СЛАУ и вектора свободных членов

СЛАУ) в ячейках (

I28:I30) получать вектор решения СЛАУ, используя

функцию умножения матриц =МУМНОЖ(

C28:E30;G28:G30). Функцию

умножения матриц возможно создать, используя мастер формул. Для этого

необходимо выделить ячейки (

I28:I30) и щелкнуть по пиктограмме MS Ex-

cel

, за тем в группе “Математические” выбрать функцию МУМНОЖ и

нажать кнопку “OK”. После появления окна “Аргументы функции” выде-

лить (при нажатой левой кнопки манипулятора “мышь”) элементы матри-

цы, обратной матрице коэффициентов СЛАУ (ячейки (

C28:E30)), щелк-

нуть левой кнопкой манипулятора “мышь” в визуальном компоненте после

метки с заголовком “Массив2”, выделить (при нажатой левой кнопки ма-

нипулятора “мышь”) элементы вектора свободных членов СЛАУ (ячейки

(

G28:G30)) и нажать кнопку “OK”. При закрытии окна “Аргументы функ-

ции” в выделенной области (ячейках (

I28:I30)) для вектора решения СЛАУ

сформируется только первый элемент вектора. Для формирования осталь-

ных элементов вектора решения СЛАУ следует нажать клавишу

F2, а за

тем при одновременно нажатых клавишах Shift и Ctrl нажать клавишу En-

ter. В результате в ячейках (

I28:I30) образуется вектор решения СЛАУ.

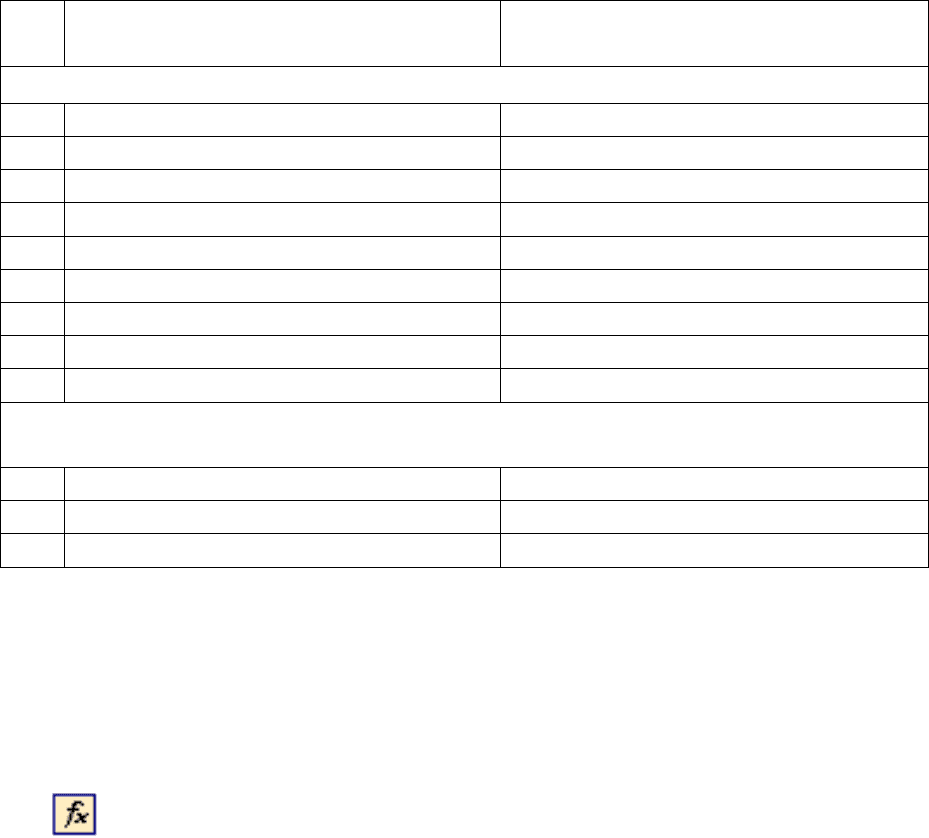
Формулы на рис. 3.1 получены в редакторе формул MS Equation 3.0,

поставляемом совестно с интегрированным пакетом прикладных программ

Microsoft Office 2003.

Лист MS Excel, представленный на рис. 1 позволяет получить вектор

решения для любой СЛАУ, состоящей из трех уравнений. Описанная тех-

нология решения СЛАУ легко позволяет решить задачу любой размерно-

сти (для любого количества уравнений в

СЛАУ).

3.1.2. Решение СЛАУ, используя метод "Поиск решения..."

(пункт главного меню "Сервис") MS Excel

Рассмотрим использование метода "Поиск решения..." на исходных

данных представленных на рис. 3.1.

Для использования метода "Поиск решения..." необходимо свести

задачу решения СЛАУ к задаче оптимизации. Введем целевую функцию

вида

()

∑∑

⎟

⎠

⎞

⎜

⎝

⎛

⋅−=

jjii

xabXF

, (3.4)

где

– i-й элемент вектора свободных членов СЛАУ;

i,j

– i, j-й элемент матрицы коэффициентов СЛАУ;

– j-й элемент вектора решения СЛАУ;

n – количество уравнений в СЛАУ.

Ограничений на вектор решения

X накладывать не будем.

Тогда математически задачу поиска вектора решения СЛАУ

X можно

записать

∑∑

⎟

⎠

⎞

⎜

⎝

⎛

⋅−=

jjii

xabX

min . (3.5)

Подобная задача (5) легко решается использованием метода "Поиск

решения..." MS Excel (см. рис. 2) следующим образом:

¾ обнуляем ячейки (B26:B28), в которых будем формировать вектор

решения СЛАУ X;

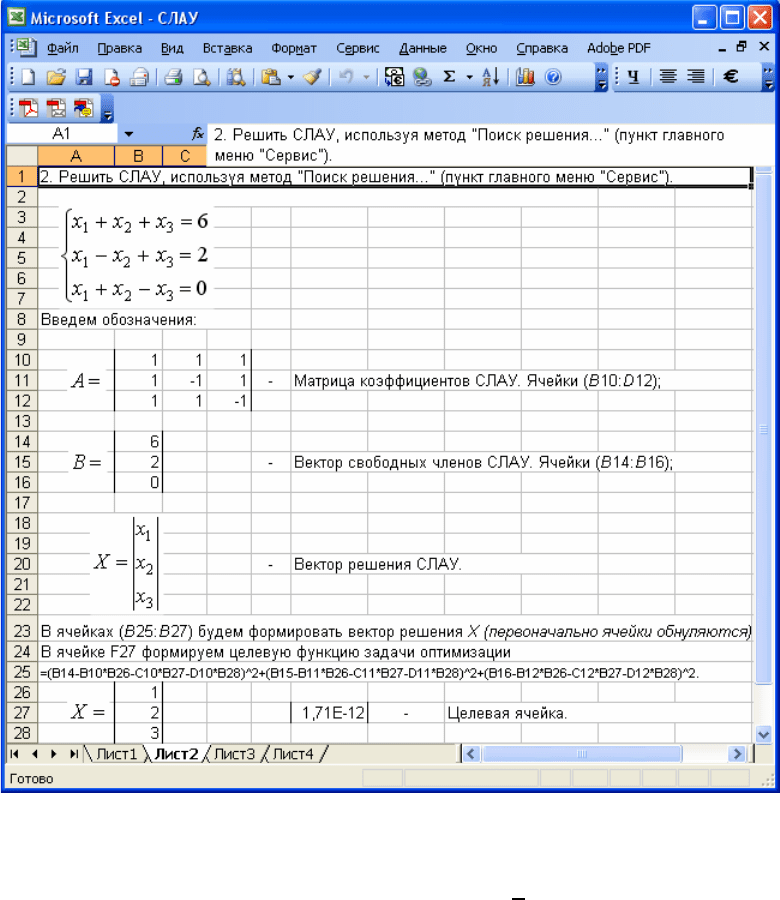
¾ для ячейки F27 в строке формул запишем

=(B14-B10*B26-C10*B27-D10*B28)^2+(B15-B11*B26-C11*B27-

D11*B28)^2+(B16-B12*B26-C12*B27-D12*B28)^2 –

правую часть целевой функции (4) для исходных данных нашей задачи;

Рис. 3.2. Решение СЛАУ, используя метод "Поиск решения..."

(пункт главного меню "Сервис") MS Excel

¾ в пункте главного меню MS Excel "Сервис" выбираем подпункт

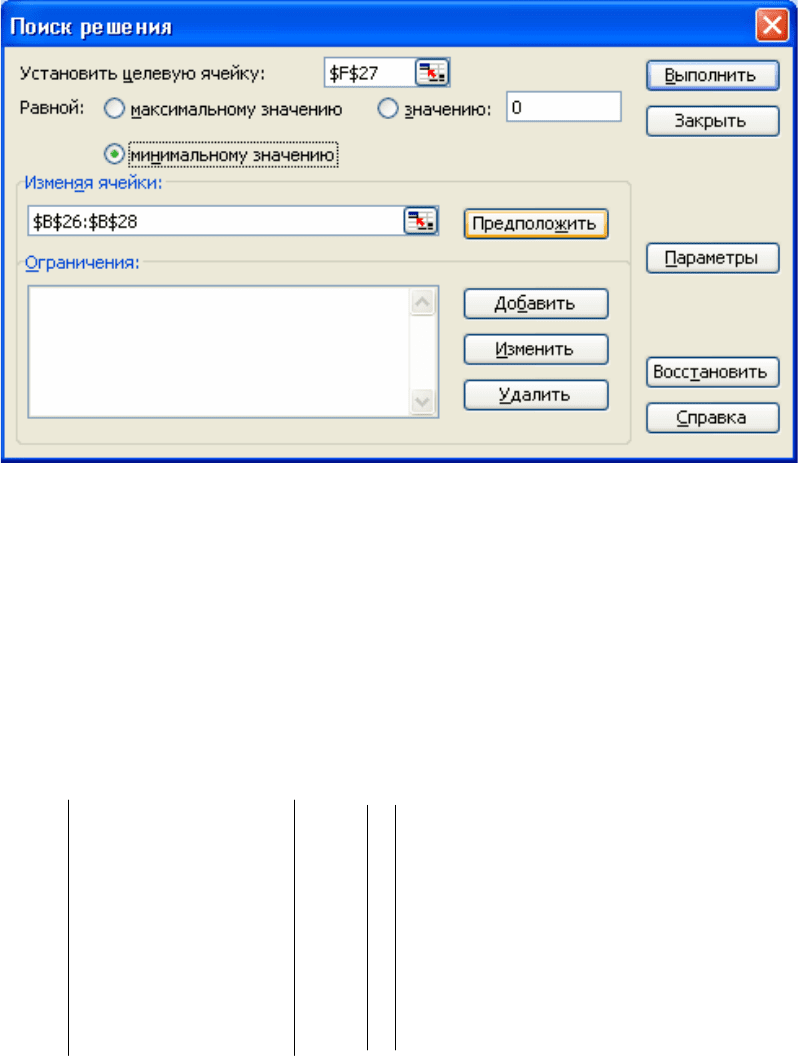
"Поиск решения..." (см. рис. 3.3).

При открытии окна "Поиск решения" напротив метки "Установить целе-

вую ячейку:" будет отражен адрес активной ячейки (ячейки, в которой был

установлен курсор при открытии окна). В ячейке $F$27 (F27) должна быть

записана формула вычисления правой части целевой функции (4). Также в

окне "Поиск решения

" ниже метки "Изменяя ячейки:" необходимо задать

адрес вектора решения СЛАУ X ($B$26:$B$28) (B26:B28). Адреса целевой

ячейки и вектора решения СЛАУ можно формировать в режиме конструк-

тора. Для этого необходимо поместить курсор в ячейку формирования со-

ответствующего адреса и на листе MS Excel выделить ячейку или массив

ячеек;

¾ нажать кнопку "Выполнить". После чего появится окно "Резуль-

таты поиска решения" и в ячейках (B26:B28) сформируется вектор реше-

ния СЛАУ X.

Рис. 3.3. Окно “Поиск решения”

Лист MS Excel, представленный на рис. 3.2 позволяет получить век-

тор решения для любой СЛАУ, состоящей из трех уравнений. Описанная

технология решения СЛАУ легко позволяет решить задачу любой размер-

ности (для любого количества уравнений в СЛАУ).

3.1.3. Решение СЛАУ методом Крамера (методом определителей)

СЛАУ из n уравнений задается матрицей коэффициентов СЛАУ A и

вектором свободных членов СЛАУ B.

nnnnn

nijii

aaaa

aaa

aaaa

,3,2,1,

,,1,

,23,22,21,2

,13,12,11,1

...

... ...

...

= ;

...

где a

i,j

– i, j-й элемент матрицы коэффициентов СЛАУ;

– i-й элемент вектора свободных членов СЛАУ.

Суть метода Крамера в следующем: сначала вычисляется определи-

тель матрицы коэффициентов СЛАУ

nnnnn

nijii

aaaa

aaa

aaaa

,3,2,1,

,,1,

,23,22,21,2

,13,12,11,1

...

... ...

...

=∆ ,

за тем вычисляются еще n определителей nj

,...,1,

∆

nnnnn

nijii

aaab

aab

aaab

,3,2,

,23,22,22

,13,12,11

...

... ...

...

=∆

nnnnn

nijiii

aaba

,3,1,

,,1,

,23,221,2

,13,111,1

...

... ...

...

=∆

,…,

nnnn

ijii

baaa

baa

baaa

...

... ...

...

3,2,1,

,1,

23,22,21,2

13,12,11,1

=∆

т.е. определитель nj

,...,1, =

∆

вычисляется для матрицы, полученной из

матрицы коэффициентов СЛАУ путем замены j-го столбца матрицы коэф-

фициентов СЛАУ вектором свободных членов СЛАУ.

Тогда элементы вектора решения СЛАУ x

, j = 1, …, n определяются

по формуле

njx

,...,1, =

∆

= .

В MS Excel существует формула

=МОПРЕД(левый_верхний_элемент_исходной_матрицы: пра-

вый_нижний_элемент_исходной_матрицы) для вычисления значений оп-

ределителей квадратных матриц.

Решение СЛАУ методом Крамера (методом определителей) пред-

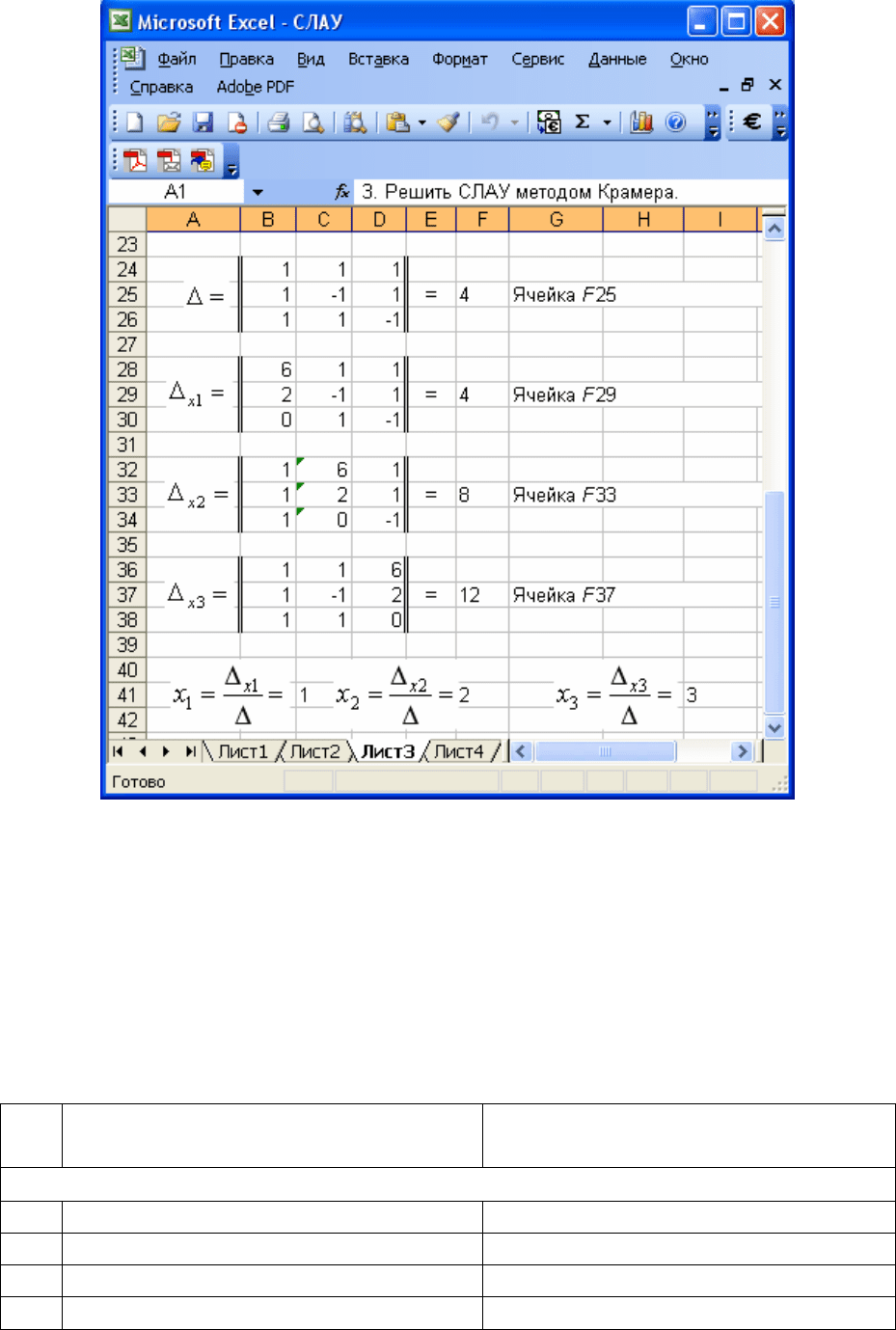
ставлено на рис. 3.4.

Рис. 3.4. Решение СЛАУ методом Крамера

Строки с 1 по 22 на рис. 3.4 не показаны, потому что они полностью

совпадают с соответствующими строками рис. 3.1, 3.2.

Необходимо сформировать матрицы для вычисления определителей

∆, ∆

, ∆

в ячейках (B24:D26), (B28:D30), (B32:D34), (B36:D38), соот-

ветственно. Алгоритм формирования матриц для вычисления определите-

лей представлен в табл. 3.2.

Табл. № 3.2

Алгоритм формирования матриц для вычисления определителей

№

п/п

Щелкнуть левой кнопкой мани-

пулятора “мышь” по ячейке

Набрать в строке формул … и

нажать Enter

Формирование матрицы для вычисления определителя ∆

1. B24 =B10

2. B25 =B11

3. B26 =B12

4. C24 =C10

№

п/п

Щелкнуть левой кнопкой мани-

пулятора “мышь” по ячейке

Набрать в строке формул … и

нажать Enter

5. C25 =C11

6. C26 =C12

7. D24 =D10

8. D25 =D11

9. D26 =D12

Формирование матрицы для вычисления определителя ∆

1. B28 =B14

2. B29 =B15

3. B30 =B16

4. C28 =C10

5. C29 =C11

6. C30 =C12

7. D28 =D10

8. D29 =D11

9. D30 =D12

Формирование матрицы для вычисления определителя ∆

1. B32 =B10

2. B33 =B11

3. B34 =B12

4. C32 =B14

5. C33 =B15

6. C34 =B16

7. D32 =D10

8. D33 =D11

9. D34 =D12

Формирование матрицы для вычисления определителя ∆

1. B36 =B10

2. B37 =B11

3. B38 =B12

4. C36 =C10

5. C37 =C11

6. C38 =C12

7. D36 =B14

8. D37 =B15

9. D38 =B16

Алгоритм вычисления определителей представлен в табл. 3.3.

Табл. № 3.3

Алгоритм вычисления определителей

№

п/п

Щелкнуть левой кнопкой мани-

пулятора “мышь” по ячейке

Набрать в строке формул … и

нажать Enter

F25 (определитель ∆)

=МОПРЕД(B24:D26)

F29 (определитель ∆

)

=МОПРЕД(B28:D30)

F33 (определитель ∆

)

=МОПРЕД(B32:D34)

F37 (определитель ∆

)

=МОПРЕД(B36:D38)

Возможно вычисление определителей в режиме конструктора. Для

этого необходимо выделить ячейку, в которой вычисляется определитель,

например, F25 и щелкнуть по пиктограмме MS Excel

, за тем в группе

“Математические” выбрать функцию МОПРЕД и нажать кнопку “OK”.

После появления окна “Аргументы функции” выделить (при нажатой ле-

вой кнопки манипулятора мышь) элементы исходной матрицы, например,

ячейки (B24:D26) и нажать кнопку “OK”.

Вектор решения СЛАУ X определяется в строке 41. Алгоритм фор-

мирования вектора решения представлен в табл. 3.4.

Табл

. № 3.4

Алгоритм формирования вектора решения СЛАУ X

№

п/п

Щелкнуть левой кнопкой мани-

пулятора “мышь” по ячейке

Набрать в строке формул … и

нажать Enter

Формирование матрицы для вычисления определителя ∆

1. C41 =F29/F25

2. F41 =F33/F25

3. I41 =F37/F25

В результате в ячейках (C41, F41, I41) сформируется вектор решения

СЛАУ X (см. рис. 3.4).

Лист MS Excel, представленный на рис. 3.4 позволяет получить век-

тор решения для любой СЛАУ, состоящей из трех уравнений. Описанная

технология решения СЛАУ легко позволяет решить задачу любой размер-

ности (для любого количества уравнений в СЛАУ).

3.2. Решение задачи линейного программирования

Рассмотрим информационную технологию задачи линейного про-

граммирования на примере следующей задачи.

Требуется определить, в каком количестве надо выпускать продук-

цию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления кото-

рой требуются ресурсы трех видов: трудовые, сырье, финансы, чтобы по-

лучить максимум прибыли. Количество ресурса каждого вида, необходи-

мое для выпуска единицы продукции данного типа, называется нормой

расхода. Нормы расхода, а также прибыль, получаемая от реализации еди-

ницы каждого типа продукции, приведены ниже в таблице.

Таблица № 3.5

Исходные данные задачи линейного программирования

Ресурс Прод1 Прод2 Прод3 Прод4 Знак Наличие

Прибыль 60 70 120 130 max -

Трудовые 1 5 1 1 <= 16

Сырье 6 5 4 3 <= 110

Финансы 4 6 10 13 <= 100

Составим математическую модель, для чего введем следующие обо-

значения:

– количество выпускаемой продукции j-го типа;

– количество располагаемого ресурса i-го вида;

– норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

– прибыль, получаемая от реализации единицы продукции j-го типа;

n – количество типов выпускаемой продукции;

m – количество ограничений на ресурсы.

Тогда задача линейного программирования в общем виде может

быть записана.

() ( )

⎪

⎭

⎪

⎬

⎫

≥

=≤⋅

→→⋅=

∑

;,...,1,

;min или max

jij

mibxa

xcXF

Задача сводится к нахождению такого вектора X, при котором целе-

вая функция F(X) принимает максимальное (или минимальное) значение с

учетом ограничений, задаваемых нестрогими линейными неравенствами

(или линейными уравнениями). В задачах линейного программирования

целевая функция F(X) тоже должна быть линейной.

Для приведенных выше конкретных

данных задача линейного про-

граммирования записывается в виде:

()

⎪

⎭

⎪

⎬

⎫

=≥

≤+++

→+++=

1,40

100131064

1103456

165

max1301207060

4321

j;x

xxxx

xxxxXF

В ячейках A8:G12 листа 2 MS (см. рис. 3.5) Exсel разместим таблицу

исходных данных задачи (см. табл. 3.5). Ячейки I22:I25 выделим для фор-

мирования вектора решения задачи

X =

. В ячейке F22 запишем выра-

жение для вычисления правой части целевой функции. В ячейках

F24:F26

сформируем формулы для вычисления левых частей ограничений (в виде

нестрогих неравенств). Формулы, записанные в ячейки

F22, F24:F26 при-

ведены в табл. 3.6.

Таблица 3.6

Формулы целевой функции и ограничений

№

п/п

Ячейка Формула

1. F22 =I22*B9+I23*C9+I24*D9+I25*E9

2. F24 =I22*B10+I23*C10+I24*D10+I25*E10

3. F25 =I22*B11+I23*C11+I24*D11+I25*E11

4. F26 =I22*B12+I23*C12+I24*D12+I25*E12

Для решения задачи линейного программирования необходимо в

пункте главного меню MS Excel “Се

рвис” выбрать подпункт “Поиск реше-

ния…”. Если в пункте главного меню MS Excel “Се

рвис” отсутствует под-

пункт “Поиск р

ешения…”, то необходимо в пункте главного меню “Сер-

вис” выбрать подпункт “Надстрой

ки” и в окне “Надстройки” поставить га-

лочку в строке “Поиск решения…”. Если же в окне “Надстройки” отсутст-

вует строка “Поиск решения…”, то следует переустановить MS Excel.