Dunajski M. Solitons, Instantons, and Twistors

Подождите немного. Документ загружается.

306 B: Complex analysis

section of O(n), n ≥ 0, is same as a global function on C

homogeneous of degree

n (a polynomial). Thus we get an extension of Liouville theorem:

Theorem B.2.4 A holomorphic function on

homogeneous of degree n > 0 is

of the form

f (Z)=φ

AB···C

···Z

for some symmetric constant ‘spinor’ φ

AB···C

Example. Tangent and cotangent bundles. Holomorphic vector ﬁelds on CP

are sections of the holomorphic tangent bundle TCP

. Holomorphic one-forms

are sections of the holomorphic cotangent bundle T

∗

. Observe that

∂

∂λ

= −λ

−2

∂

and dλ = −λ

λ.

We absorb the minus signs into the local trivializations, and deduce that

= O(2) and T

∗

= O(−2).

Therefore a global section of T

is of the form

(uλ

+ xλ + v)

dλ

, (B5)

for (u, x,v) ∈

and there are no global section of T

∗

Example. To any rank-k vector bundle E we assign a line bundle det E := 

(E).

It has transition functions det F

αβ

. Deﬁne the canonical bundle K of M to be

det(T

∗

M). This is the line bundle of holomorphic volume forms. On CP

have an isomorphism K

∼

O(−2).

The theorem of Grothendieck states that all holomorphic line bundles over a

rational curve are equivalent to O(n) for some n. In fact more is true

Theorem B.2.5 (Birkhoff–Grothendieck) A rank-k holomorphic vector bundle

E →

is isomorphic to a direct sum of line bundles O(m

) ⊕···⊕O(m

) for

some integers m

This theorem is proved for example in [121].

Therefore for a rank k vector bundle the transition matrix

F :

∗

→ GL(k, C)

can be written in the form

F =

H diag (λ

−m

,...,λ

−m

−1

where H : U → GL(k,

C) and

H :

U → GL(k, C) are holomorphic.

Example. Let E

be a one-parameter family of rank-two vector bundles over CP

determined by a patching matrix

F =



λ t

0 λ

−1



B.3

Cech cohomology 307

For t =0,F is already in the form given by the Birkhoff–Grothendieck theorem,

with H =

H =1,m

= −1, and m

=1.Butfort = 0, we have

F =



0 t

−t

−1



−1

λ 1



, (B6)

so that m

= m

= 0 by Lemma B.2.2. Therefore E

" O(1) ⊕ O(−1), but E

the trivial bundle for t = 0. This is an example of ‘jumping’: as t changes through

0, the holomorphic structure of the bundle changes discontinuously, in spite of

the fact that the bundles E

are all the same (and all trivial) from the topological

point of view.

B.3

Cech cohomology

An element of the ﬁrst cohomology group of E → M relative to the cover U

of M

is a map that assigns a holomorphic section f

αβ

∈ (U

∩ U

) to each non-empty

intersection such that

αβ

+ f

βα

= 0 and f

αβ

+ f

βγ

+ f

γα

=0.

Two such maps f and f



are equivalent iff



αβ

− f

αβ

= h

− h

(the RHS is called a co-boundary) where h

is a holomorphic section of E over

. The ﬁrst cohomology group is a quotient of the additive group { f

αβ

} by this

relation. (The deﬁnition is in fact independent of the covering chosen [121].) A

more concrete deﬁnition can be used if it is possible to choose an open cover

consisting on two pseudo-convex sets U and

(M, E)=

(U ∩

U, E)

(U, E)+(

U, E).

We will ﬁnd H

(CP

, O(k)). This is the space of functions f

holomorphic on

∩ U

and homogeneous of degree k in coordinates [Z

, Z

], modulo cobound-

aries. In a trivialization over U

= Uf

is represented by a holomorphic function

f on

∗

. In the trivialization over U

U, f

is represented by λ

−k

f . For k ≥−1

we can write

f =

∞



−∞

= λ

h − h,

where

h = −

∞



and

h =

∞



−i

−i−k

308 B: Complex analysis

are holomorphic in U and

U, respectively. Therefore f ∼ 0, and the ﬁrst cohomol-

ogy group vanishes. The splitting is not unique unless k = −1, as we are free to set

the ﬁrst k + 1 terms in h to 0 by modifying

If k ≤−2 we have f = λ

h − h + q, where

−h =

∞



h =

∞



−k

−i

−i−k

, and q =

−k−1



−i

The functions h and

h are holomorphic in U and

U, respectively, therefore f ∼ q,

and the class of f is uniquely determined by the coefﬁcients f

−1

,..., f

k+1

.We

conclude that

(CP

, O(k)) =



0fork > −2

−k−1

for k ≤−2.

(B7)

Therefore f ∈ H

(CP

, O(−1)) can be split uniquely, as f =

h − h. We shall often

use the explicit form of this splitting:

h =

2πi





f (ζ )

λ − ζ

dζ and

h =

2πi





f (ζ )

λ − ζ

dζ, (B8)

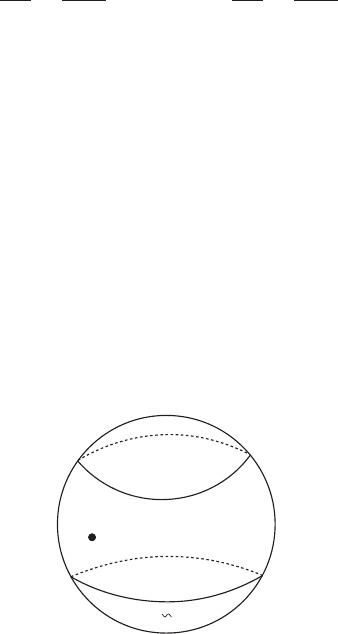
where ζ is an afﬁne coordinate on

(Figure B.1). The contours  and

 are

homologous to the equator of

in U ∩

U and are such that  −

 surrounds the

point λ = ζ . We see that f =

h − h follows from the Cauchy’s integral formula.

Given f ∈ H

(CP

, O(k)), k > −1, we may divide it by a homogeneous polyno-

mial of degree k + 1, and apply (B8) to the quotient. The non-uniqueness of this

procedure (the choice of the polynomial) is measured by H

(CP

, O(k + 1)).

B.3.1 Deformation theory

Let L be a complex submanifold of a complex manifold Z. The normal bundle

N(L) → L is deﬁned to be ∪

ζ ∈L

(L) where N

=(T

Z)/(T

L) is a quotient vector

space.

The following result of Kodaira underlies the twistor approach to curved geome-

tries. Let Z be a complex manifold of dimension d + r. A pair (F , M) is called a

complete analytic family of compact submanifolds of Z of dimension d if

Î = Ê

Figure B.1 Splitting formula

B.3

Cech cohomology 309

F is a complex analytic submanifold of Z × M of co-dimension r with the

property that for each t ∈ M the intersection L

× t := F ∩ (Z ×t) is a compact

submanifold of Z × t of dimension d.

There exists an isomorphism

M " H

, N

) (B9)

where L

⊂ Z is submanifold of Z and N

−→ L

is the normal bundle of L

Theorem B.3.1 (Kodaira [95]) Let L be a d-dimensional complex compact sub-

manifold of a complex manifold Z, and let N be the normal bundle of L in Z.If

(L, N)=0then there exists a complete analytic family of compact submanifolds

(F, M) such that L = L

for some t

∈ M.

In Chapter 10 we apply the above theorem to the situation when Z is a twistor

space and L =

. Roughly speaking, the moduli space M is the ‘arena’ of

differential geometry and integrable systems. One way to analyse such moduli

spaces is to consider inﬁnitesimal deformations and to exponentiate them.

APPENDIX C

Overdetermined PDEs

C.1 Introduction

This appendix treats geometric approaches to DEs, both ODEs and PDEs.

Geometry in this context means that certain results do not depend on coordinate

choices made to write down a DE, and also that structures like connection and

curvature are associated to DEs.

The subject can get very technical but we shall take a low-technology approach.

This means that sometimes, for the sake of explicitness, a coordinate calculation

will be performed instead of presenting an abstract coordinate-free argument.

We shall also skip some proofs, and replace them by examples illustrating the

assumptions and applications. The proofs can be found in [23] (see also [90] and

[151]).

Given a system of DEs it is natural to ask the following questions:

Are there any solutions?

If yes, how many?

What data is sufﬁcient to determine a unique solution?

How to construct solutions?

These are all local questions, that is, we are only interested in a solution in a small

neighbourhood of a point in a domain of deﬁnition of dependent variables. We

shall mostly work in the smooth category, except when a speciﬁc reference to the

Cauchy–Kowalewska theorem is made. This theorem holds only in the real analytic

category.

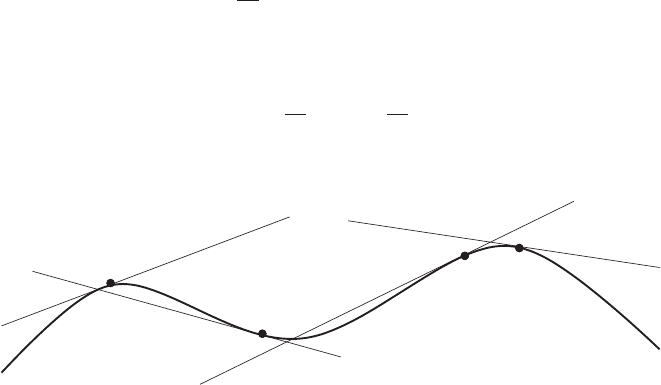
Problem 1. Consider an ODE

= F (x, u) (C1)

where F and ∂

F are continuous

in some open rectangle

U = {(x, u) ∈

, a < x < b, c < u < d}.

The Picard theorem states that for all (x

, u

) ∈ U there exists an interval I ⊂ R

containing x

such that there is a unique function u : I → R which satisﬁes (C1)

In fact it is sufﬁcient if F is Lipschitz.

C.1 Introduction 311

and such that u(x

)=u

. We say that the general solution to this ﬁrst-order ODE

depends on one constant. The unique solution in Picard theorem arises as a limit

u(x) = lim

n→∞

(x)

of a uniformly convergent sequence of functions {u

(x)} deﬁned iteratively by

n+1

(x)=u



F (t, u

(t))dt.

One can treat a system of n ﬁrst-order ODEs with n unknowns in the same way:

The unique solution depends on n constants of integration.

The conditions in Picard theorem always need to be checked and should not be

taken for granted. For example, the ODE

= u

1/2

, u(0) = 0

has two solutions in any neighbourhood of (0, 0): u(x)=0andu(x)=x

/4.

More geometrically, the solutions to (C1) are curves tangent to a vector ﬁeld

X =

∂

∂x

+ F (x, u)

∂

∂u

The Picard theorem states that the tangent directions always ﬁt together to form a

curve.

One can rephrase this in a language of differential forms. The one-form annihilated

by X is (a multiple of) θ = du − Fdx and a parameterized curve x → (x, u(x)) is

an integral curve of (C1) if θ (or any of its multiples) vanishes on this curve. In

general, if θ is a k-form on a manifold M the submanifold S ⊂ M is an integral of

θ if f

∗

(θ)=0,where f : S → M is an immersion.

We aim to reformulate systems of DEs as the vanishing of a set of differential

forms (in general of various degree). This gives a coordinate invariant formulation

of DEs as exterior differential systems (EDSs), and allows a discussion of the

dimension of integral manifold.

Problem 2. Consider a system of PDEs

= A(x, y, u) and u

= B(x, y, u), (C2)

where u

= ∂

u, etc. Both derivatives of u are determined at each point (x, y, u) ∈

where A, B, A

, and B

are continuous. This gives rise to a two-dimensional

312 C: Overdetermined PDEs

plane spanned by two vectors

∂

∂x

+ A

∂

∂u

and X

∂

∂y

+ B

∂

∂u

Do these planes ﬁt together to form a solution surface in a neighbourhood of (say)

(0, 0, u

) ∈ R

? Let us try two successive applications of Picard theorem.

Set y =0, u(0, 0) = u

. The Picard theorem guarantees the existence of the unique

u(x) such that

= A(x, 0,

u),

u(0) = u

Consider

u(x) and hold x ﬁxed, regarding it as a parameter. Picard theorem gives

the unique u(x, y) such that

= B(x, y, u), u(x, 0) =

u(x).

We have therefore constructed a function u(x, y) but it may not satisfy the original

PDE (C2) which is overdetermined and requires that the compatibility condition

)

=(u

)

holds. Expanding the mixed partial derivatives yields

− B

+ A

B − B

A =0. (C3)

Do we need more compatibility conditions arising from differentiating (C3) and

using (C2) to get rid of u

, u

? The answer is no. This follows from the Frobenius

theorem which we are going to prove in Section C.2 (the LHS of (C3) is the

obstruction to the vanishing of the commutator [X

, X

]). If (C3) holds then

solving the pair of ODEs gives the solution surface depending on one constant.

What happens if (C3) does not hold?

If u does not appear in (C3) then (C3) is a curve in R

and there is no solution in

an open set containing (0, 0, u

If (C3) gives an implicit algebraic relation between (x, y, u), then solve this

relation to get a surface (x, y) → (x, y, u(x, y)). This may or may not be a solution

to the original pair of PDEs (C2). In particular the initial condition may not be

satisﬁed.

This simple example raises a number of questions. How should we deal with more

complicated compatibility conditions? When can we stop cross-differentiating?

Theorems C.3.1 and C.3.2 proved in Section C.3 and more generally the Cartan

test (Theorem C.6.5) discussed in Section C.6 give some of the answers.

Problem 3. Consider a system of linear PDEs

= αu + βv, u

+ v

= γ u + δv, and v

= u + φv, (C4)

C.1 Introduction 313

where α,β,...,φ are some functions of (x, y) deﬁned on an open set U ⊂ R

. This

is an overdetermined system as there are three equations for two unknowns, but

(unlike the system (C2)) it is not overdetermined enough, as the partial derivatives

are not speciﬁed at each point. Therefore we cannot start the process of building

the solution surface as we cannot specify the tangent planes. One needs to use

the process of prolongation and introduce new variables for unknown derivatives

hoping to express derivatives of these variables using the (differential consequences

of) the original system. In our case it is enough to deﬁne

w = u

− v

(there are other choices, e.g. w = u

, but the solution surface will not depend on

the choices made). Now

(γ u + δv + w) and v

(γ u + δv − w),

and we can impose the compatibility conditions

)

=(u

)

, and (v

)

=(v

)

These conditions will lead to expressions

= ... and w

= ...,

where (...) denote terms linear in (u,v,w). The system is now closed as ﬁrst

derivatives of (u,v,w) are determined at each point thus specifying a family of

two-dimensional planes in

. Do these two planes ﬁt in to form a solution surface

(x, y) −→ (x, y, u(x, y),v(x, y),w(x, y))

? Not necessarily, as there are more compatibility conditions to be imposed

(e.g. (w

)

=(w

)

). These additional conditions will put restrictions of the func-

tions (α,β,...,φ). In Section C.4 we shall see how to deal with the prolongation

procedure systematically.

This simple example of prolongation arises naturally in the geometry of surfaces.

Assume you are given a metric (a ﬁrst fundamental form) on a surface

g = Edx

+2Fdxdy+ Gdy

Does there exist a one-form K = udx + vdy such that the Killing equations

∇

= 0 and x

=(x, y)

are satisﬁed, where ∇ is the Levi-Civita connection of g? Expanding the Killing

equations in terms of the Christoffel symbols leads to the system (C4) where the

six functions (α,β,...,φ) are given in terms of E, F, G, and their derivatives.

The consistency conditions for the prolonged system to admit non-zero solutions

give differential constraints on E, F , and G. These constraints can be expressed

in tensor form as differential invariants of the metric g. In Section C.4.1 we

shall discuss an approach to constructing such invariants and ﬁnd necessary and

sufﬁcient conditions of a metric g to admit a Killing vector.

314 C: Overdetermined PDEs

C.2 Exterior differential system and Frobenius theorem

Deﬁnition C.2.1 An EDS is a pair (M, I) where M is a smooth manifold and

I ⊂ 

∗

(M) is a graded differential ideal in a ring of differential forms that is closed

under exterior differentiation:

dθ ∈ I if θ ∈ I.

For example, the set of forms

{dy − pdx, dp ∧ dx, dx}

gives EDS where M =

. We shall use the following notation: I

= I ∩ 

(M)is

a set of all forms of degree k in I. The evaluation of a form θ at x ∈ M will be

denoted θ

and I

will denote the evaluation of all forms in I at x.

One way to present an EDS is by specifying the set of differential generators

<θ

,...,θ

diff

:= {γ

∧ θ

,...,γ

∧ θ

,β

∧ dθ

,...,β

∧ dθ

where γ and β are arbitrary differential forms. We shall assume that none of the

generators are zero-forms (i.e. functions). Otherwise we shall restrict the EDS to

submanifolds on which these functions vanish. An EDS whose generators are one-

forms is called a Pfafﬁan system.

We shall also use the notation

<θ

,...,θ

alg

:= {γ

∧ θ

,...,γ

∧ θ

}

to denote the set of forms generated algebraically by exterior multiplication.

Deﬁnition C.2.2 An integral manifold of I is a submanifold f : S → M such that

∗

(θ)=0for all θ ∈ I.

In particular S is an integral submanifold of I = <θ

,...,θ

diff

iff f

∗

(θ

)=0.

Example. A system of N ﬁrst-order ODEs

= F

(x, u

,...,u

),α=1,...,N

is modelled by the EDS I generated by N one-forms <du

− F

dx>

diff

on an

open set in

N+1

. The integral manifolds of this EDS are integral curves of the

vector ﬁeld

X =

∂

∂x



α=1

∂

∂u

which annihilates all forms in I.

Example. The pair of PDEs u

= A(x, y, u) and u

= B(x, y, u) is modelled by an

ideal generated by one one-form

I = <du − Ad x − Bdy>.

C.2 Exterior differential system and Frobenius theorem 315

The vectors ∂

+ A∂

and ∂

+ B∂

annihilating this one-form are tangent to the

integral surface if one exists. There are no integral surfaces if the compatibility

(C3) does not hold.

Two EDSs (M, I) and (

I) are equivalent if there exist a diffeomorphism such

that

f : M −→

M and f

∗

(

I)=I.

This notion can be applied to determine whether two systems of DEs are equivalent

and, in particular, to linearize some DEs. In the next two examples we shall use the

following notation: if θ = θ

,...,x

) dx

then

θ = θ

(

,...,

) d

where x

and

are local coordinates on M and

M, respectively.

Example. Consider the Monge–Ampere equation

− u

=1,

where u = u(x, y). This non-linear equation is modelled by the EDS

<θ

= du − pdx − qdy,θ

= dp ∧ dq − dx ∧ dy>

diff

(C5)

. In particular, it is not a Pfafﬁan system. Consider f : R

→ R

given by

f (x, y, u, p, q)=(

q):=(x, q, u − qy, p, −y).

We verify that

∗

(

)=d

u −

x −

y = du − pdx −qdy and

∗

(

)=d

p ∧ d

q − d

x ∧ d

y = dy ∧ dp + dq ∧ dx.

The integral manifolds of the pulled-back ideal are

du − pdx − qdy = 0 and dy ∧dp + dq ∧ dx =0.

Vanishing of the one-form gives p = u

, q = u

, and vanishing of the two-form

gives the linear Laplace equation

+ u

=0.

Some care needs to be taken with this example: We have established a one-to-

one correspondence between integral surfaces of the Laplace equation and the

Monge–Ampere equation, but not between solutions as some integral surfaces

may have dx ∧ dy =0.

Example. A similar procedure can be used to reduce the general four-dimensional

Ricci-ﬂat Kähler metric with a tri-holomorphic Killing vector to the Gibbons–

Hawking form where the non-linear Ricci-ﬂat condition reduces to the Laplace

equation on

. Consider a Kähler metric in an open ball in C

with local

holomorphic coordinates (w, z) given in terms of the (non-holomorphic) Kähler

potential  :

−→ R:

g = 

w ¯w

dw d ¯w + 

dw d

z + 

z ¯w

dzd ¯w + 

dzd

z. (C6)