Dunajski M. Solitons, Instantons, and Twistors

Подождите немного. Документ загружается.

276 10 : Anti-self-dual conformal structures

and the second heavenly equation (10.2.22) arises from the vanishing of the

coefﬁcient of λ

in  ∧ .

Example. This example is modiﬁed from [83] to allow the application of the

heavenly formalism. Take the Hamiltonian f ∈ H

(PT , O(2)) deﬁning the

deformation (10.5.112) to be

f =

(ω

)

4π



The deformation equations (10.5.112)

dω

= 0 and

dω

(ω

)



integrate to

˜ω

= ω

and ˜ω

= ω

+ t

(ω

)



Therefore ω

gives a global holomorphic function on CP

homogeneous of

degree one, so by the Liouville theorem (Theorem B.2.4) it must be linear,

that is,

= π



y + π



for some complex numbers (y,w). Substituting this in the formula for ˜ω

gives an expression homogeneous of degree one:

˜ω

−

(π



)



− 3π



y − 3π



twy

= ω

(π



)



The LHS is holomorphic around π



=(1, 0) and the RHS is holomorphic

around π



=(0, 1). Thus, again applying the Liouville theorem, we deduce

that this expression deﬁnes a linear function, say π



z − π



x, for some com-

plex numbers (z, x). Rearranging gives

= π



z − π



x −

(π



)



The four complex numbers (w, z, x, y) parameterize the family of curves, and

serve as local coordinates on the ASD Ricci-ﬂat four-manifold M.

We can now read off the functions (P, Q) from the formula (10.5.113):

P = w + λy and Q = z − λx − λ

. (10.5.115)

Comparing this with (10.5.114) gives the second heavenly potential

10.5 Twistor theory 277

Finally the ASD Ricci-ﬂat metric (10.2.13) is

g = dwdx + dzdy − 3ty

. (10.5.116)

The ASD Weyl curvature in the second heavenly formalism is given by

ABC D

∂

∂x

, (10.5.117)

where x

=(y, −x). Therefore our simple example is of Petrov–Penrose type

N and has constant curvature – the only non-vanishing component being

0000

=6t, where t is a constant deformation parameter.

We shall re-derive the expression for the metric using the Penrose’s original

prescription presented in the proof of Theorem 10.5.5 without referring

to the heavenly formalism. In this approach the conformal structure on

the moduli space of lines parameterized by x

=(w, z, x, y) is calculated by

determining the quadratic condition for a section of the normal bundle to

a twistor line to vanish. The sections of the normal bundle to the curve

(10.5.115) correspond to tangent vectors and sections with one zero will

determine null vectors and therefore the conformal structure. Now take the

variation of P(λ) and Q(λ) for a small change δx

to obtain

δ P = δw + λδy = 0 and δ Q = δz − λδx − 3λ

δy =0.

Substituting λ = −δw/δy from the ﬁrst expression to the second and multi-

plying the resulting expression by δy we ﬁnd that the conformal structure

is represented by the metric (10.5.116). The conformal factor now needs to

be determined from (10.5.108) to ensure that the resulting metric is Ricci-

ﬂat. We ﬁnd that this conformal factor is a constant in agreement with the

calculation based on the heavenly formalism.

Example. The second heavenly equation (10.2.22) with

= 0 can be

expressed as

∧ dx ∧ dy + dw ∧ d

∧ d

=0. (10.5.118)

Introduce p :=

and perform a Legendre transform

F (p, y,w):=px(w, y, p) − (w, y, x(w, y, p)).

Then x = F

= −F

and (10.5.118) yields the wave equation [65] (which

in Riemannian signature is the Laplace equation on R

+ F

=0. (10.5.119)

Implicit differentiation gives

= −F

= −

, and

278 10 : Anti-self-dual conformal structures

and so (with the help of (10.2.13) and (10.5.119))

g = F

(

+ dwdp) −

(dz −

dy + F

dw)

= V(

+ dwdp) − V

−1

(dz + A)

, (10.5.120)

where V = F

and A = F

dw − (F

/2)dy satisfy the monopole equation

(9.4.36) which follows from (10.5.119). Thus (10.5.120) is the complexiﬁed

Gibbons–Hawking metric (9.4.35).

The twistor description is as follows: The vanishing of

implies that the

whole series (10.5.113) for ω

truncates at second order. Thus the twistor

space admits a global holomorphic function of degree two given by π



(i.e. PT ﬁbres holomorphicaly over the total space of the line bundle O(2)),

and this is the Hamiltonian with respect to , for the holomorphic vector

ﬁeld corresponding to the tri-holomorphic Killing ﬁeld ∂

= K



∂



M. Conversely, given a tri-holomorphic symmetry, the tri-holomorphicity

condition means that its lift to the spin bundle M is horizontal and so on

twistor space, the corresponding holomorphic vector ﬁeld is tangent to the

ﬁbres of µ. It also preserves  and so is Hamiltonian with Hamiltonian given

by a homogeneity degree-two global function. We can choose ω

to be this

preferred section divided by π



so that the series for ω

terminates after λ

Substituting the Legendre transform into (10.5.113) yields

P = w + λy − λ

p and

Q = z − λF

+ λ

+ ···,

where F = F (w, y, p). With the deﬁnition  = dω

∧ dω

λ=const

(10.5.119)

follows from  ∧  =0. The basis of SD two-forms can be read off from

 = 







= −dz ∧ dp + dy ∧ dF

− dw ∧ dF

,



= dz ∧ dy + dw ∧ dF

and 



= dz ∧ dw,

and these determine the metric above.

This example is a starting point to constructing ASD Ricci-ﬂat metric

without Killing vectors. One assumes that the twistor space admits a holo-

morphic ﬁbration over a total space of the line bundle O(2k) for some k > 2.

In this case the series for ω

truncates after 2k + 1 terms, and the function F

in the series for ω

is a solution of a system of overdetermined but consistent

PDEs generalizing the Laplace equation. See [14, 49, 106] for details.

10.5 Twistor theory 279

10.5.2.3 Recursion operator and twistor functions

Given a solution φ

∈ W

to the background-coupled wave equation (10.2.24),

deﬁne, for i ∈ Z, a hierarchy of linear ﬁelds, φ

≡ R

. Deﬁne a function

on the correspondence space by  =



∞

−∞

and observe that the recur-

sion equations (10.2.27) are equivalent to L

 = 0. Thus  is a function

on the twistor space PT . Conversely every solution of L

 = 0 deﬁned on

a neighbourhood of |λ| = 1 can be expanded in a Laurent series in λ with

the coefﬁcients forming a series of elements of W

related by the recursion

operator. It is clear that a series corresponding to Rφ

is the function λ

−1

,

thus we deﬁne R = /λ.

We can in this way build coordinate charts on twistor space from those on

M arising from the choices in the heavenly equations. Put ω

= w

=(w, z); the

surfaces of constant ω

are twistor surfaces. We have that ∇



= 0 so that

in particular ∇



∇



= 0 and if we deﬁne ω

= R

then we can choose

= 0 for negative i. We deﬁne

∞



i=0

. (10.5.121)

We can similarly deﬁne ˜ω

by ˜ω

=˜w

and choose ˜ω

=0 for i > 0. Note

that ω

and ˜ω

are solutions of L

holomorphic around λ = 0 and λ = ∞,

respectively, and they can be chosen so that they extend to a neighbourhood of

the unit disc and a neighbourhood of the complement of the unit disc and can

therefore be used to provide a patching description (10.5.110) of the twistor

space.

The recursion operator acts on linearized perturbations of the ASD Ricci-ﬂat

equations. Under the twistor correspondence, these correspond to linearized

holomorphic deformations of (part of) PT . Consider the inﬁnitesimal version

of (10.5.112) given by

δ ˜ω

∂δf

∂ ˜ω

. (10.5.122)

If the ASD Ricci-ﬂat metric is determined by a solution to the second

heavenly equation (10.2.22) then δ f is a linearized deformation of the twistor

space corresponding to δ ∈ W

. The recursion operator acts on linearized

deformations as follows:

Proposition 10.5.6 Let R be the recursion operator deﬁned by (10.2.27). Its

twistor counterpart is the multiplication operator

R δ f =



δ f = λ

−1

δ f. (10.5.123)

280 10 : Anti-self-dual conformal structures

(Note that R acts on δ f without ambiguity; the ambiguity in boundary condi-

tion for the deﬁnition of R on space-time is absorbed into the choice of explicit

representative for the cohomology class determined by δ f .)

Proof Pull back δ f to the primed spin bundle S



on which it is a coboundary

so that

δ f (π



, x

)=h(π



, x

) −

h(π



, x

), (10.5.124)

where h and

h are holomorphic on U and

U, respectively (here we abuse

notation and denote by U and

U the open sets on the spin bundle that are the

preimage of U and

U on twistor space). A choice for the splitting (10.5.124) is

given by (compare (B8))

h =

2πi





(π



)

(ρ



)(ρ



)

δ f (ρ



)ρ



dρ



and (10.5.125)

h =

2πi





(π



)

(ρ



)(ρ



)

δ f (ρ



)ρ



dρ



Here ρ



are homogeneous coordinates of CP

pulled back to the spin bundle.

The contours  and

 are homologous to the equator of CP

in U ∩

U and are

such that  −

 surrounds the point ρ



= π



The functions h and

h are homogeneous of degree two in π



and do not

descend to PT , whereas their difference does so that



∇



h = π



∇



h = π







, (10.5.126)

where the ﬁrst equality shows that the LHS is global with homogeneity degree

three and implies the second equality for some 



which will be the

third potential for a linearized ASD Weyl spinor. 



is in general deﬁned

modulo terms of the form ∇

A( A



)

but this gauge freedom is partially ﬁxed

by choosing the integral representation above; h vanishes to third order at



= o



and direct differentiation, using ∇



δ f = ρ



δ f

for some δ f

, gives





= o



∇



δ where

δ =

2πi





δ f

(ρ



)



dρ



. (10.5.127)

This is consistent with the Pleba

nski gauge choices leading to (10.2.22). The

condition

∇

A(D







)

follows from (10.5.126) which, with the Pleba

nski gauge choice, implies δ ∈

. Thus we obtain a twistor integral formula for the linearization of the

second heavenly equation.

10.5 Twistor theory 281

Now recall formula (10.2.27) deﬁning R. Let Rδ f be the twistor function

corresponding to Rδ by (10.5.127). The recursion relations yield





Rδ f

(ρ



)



dρ







δ f

(ρ



)

(ρ



)



dρ



so Rδ f = λ

−1

δ f . 

10.5.2.4 Hidden symmetry algebra

The ASD Ricci-ﬂat equations in the Pleba

nski forms (10.2.18) or (10.2.22)

have a residual coordinate symmetry. This consists of area-preserving dif-

feomorphisms in the w

coordinates together with some extra transforma-

tions that depend on whether one is reducing to the ﬁrst or second form.

By regarding the inﬁnitesimal forms of these transformations as linearized

perturbations and acting on them using the recursion operator, the coordinate

(passive) symmetries can be extended to give ‘hidden’ (active) symmetries of

the heavenly equations. Formulae (10.5.127) and (10.5.123) can be used to

recover the relations of the hidden symmetry algebra of the heavenly equations.

Let V be a volume-preserving vector ﬁeld on M. Deﬁne δ



:= [V, e



where e



is a null tetrad of the metric. This is a pure gauge transformation

corresponding to the addition of Lie

g to the space-time metric and preserves

the ﬁeld equations. Note that

[δ

,δ



:= δ

[V,W]



Once a Pleba

nski coordinate system and reduced equations have been

obtained, the reduced equation will not be invariant under all the SDiff(M)

transformations, where SDiff(M) is the group of volume-preserving diffeomor-

phisms of M. The second form (10.2.22) will be preserved if we restrict our-

selves to transformations which preserve the SD two-forms 



= dw

∧ dw

and 



= dx

∧ dw

. The conditions Lie





= Lie





= 0 imply that V

is given by

V =

∂h

∂w

∂

∂w



∂k

∂w

− x

∂

∂w



∂

∂x

where h = h(w

) and k = k(w

). The four-manifold M is now viewed as a

cotangent bundle M = T

∗



with w

being coordinates on a two-dimensional

complex manifold 

. The full SDiff(M) symmetry breaks down to the semi-

direct product of SDiff(

), which acts on M by a Lie lift, with (

, O) which

acts on M by translations of the zero section by the exterior derivatives of

functions on 

. Let δ

correspond to δ



∂

∂x

∂

∂x

282 10 : Anti-self-dual conformal structures

This gives the pure gauge elements in the second heavenly equation. These

symmetries take a solution to an equivalent solution. The recursion operator

can be used to deﬁne an algebra of ‘hidden symmetries’ that take one solution

to a different one as follows: Let δ

be a pure gauge which also satisﬁes



=0.Weset

:= R

∈ W

Proposition 10.5.7 Generators of the hidden symmetry algebra of the second

heavenly equation satisfy the relation

[δ

,δ

]=δ

[V,W]

i+ j

. (10.5.128)

Proof Let δ

f be the twistor function corresponding to δ

(by (10.5.127))

treated as an element of (U ∩

U, O(2)) rather than H

(PT , O(2)). Deﬁne

[δ

,δ

]by

[δ

,δ

] :=

2πi



{δ

f,δ

f }

(π



)



dπ



where the Poisson bracket is calculated with respect to a canonical Poisson

structure on PT . From Proposition 10.5.123 it follows that

[δ

,δ

] =

2πi



−i−j

{δ

f,δ

f }

(π



)



dπ



= R

i+ j

[V,W]

as required. 

10.5.2.5 Hierarchies

The twistor space PT

for a solution to the hierarchy (10.2.29) associated

to the Lax system (10.2.30) on N is obtained by factoring the correspon-

dence space N × CP

by the twistor distribution L

. One can repeat the

steps leading to the proof of Theorem 10.5.5 to show that PT

is a three-

dimensional complex manifold which holomorphically ﬁbres over CP

such

that the sections of this ﬁbration have normal bundle O(n) ⊕ O(n) and there

exists a non-degenerate two-form  on the ﬁbres of µ : PT

→ CP

, with

values in the pull-back from CP

of O(2n).

One can then ﬁnd the twistor spaces for the four-dimensional hyper-Kähler

slices given by x

= const, i ≥ 2 by taking a sequence of n − 1 blow-ups of

points in the ﬁbre over o



∈ CP

, the choice of point in the ﬁbre to blow up at

the (n − i + 1)th blowup corresponding precisely to the choice of the values of

. See [45, 49] for details of this construction.

10.5 Twistor theory 283

10.5.3 Twistor theory and symmetries

In Section 10.3 we discussed the appearance of EW structures and projec-

tive structures in the cases of a non-null and null conformal Killing vectors,

respectively. In both cases there is a twistor correspondence which arises as a

symmetry reduction of Theorem 10.5.3.

Given a four-dimensional holomorphic ASD conformal structure, its twistor

space is the space of α-surfaces. A conformal Killing vector preserves the

conformal structure, so preserves α-surfaces, giving rise to a holomorphic

vector ﬁeld on the twistor space. If the Killing vector is non-null then the vector

ﬁeld on twistor space PT is non-vanishing. This is because a non-null Killing

vector is transverse to any α-surface. In this case one can quotient the three-

dimensional twistor space by the induced vector ﬁeld, and it can be shown

[93] that the resulting two-dimensional complex manifold contains CP

’s with

normal bundle O(2).

Theorem 10.5.8 (Hitchin [79]) There is a one-to-one correspondence between

solutions to EW equations (10.3.41) and two-dimensional complex manifolds

admitting a three-parameter family of rational curves with normal bundle

O(2).

In this twistor correspondence the points of W correspond to rational O(2)

curves in the complex surface Z and points in Z correspond to totally geodesics

null surfaces in W. The conformal structure [h] arises as we deﬁne the null

vectors at p in W to be the sections of the normal bundle N(L

) which vanish

at some point to second order. A section of O(2) has the form V



thus the vanishing condition (V



)

− V



is quadratic. To deﬁne the

connection D we deﬁne a direction at p ∈ W to be a one-dimensional space

of sections of O(2) which vanish at two points Z

and Z

in L

. The one-

dimensional family of O(2) curves in Z passing through Z

and Z

gives a

geodesic curve in W in a given direction. In the limiting case Z

= Z

these

geodesics are null with respect to [h] in agreement with (10.3.40).

The dispersionless integrable systems described in Section 10.3.1 can be

encoded in the twistor correspondence of Theorem 10.5.8 if the twistor

space admits some additional structures. The coordinate equivalence classes

of solutions to the SU(∞)-Toda equations correspond to twistor spaces with

a preferred section of κ

−1/2

, where κ is the canonical bundle of Z (see [104]

for details). The solutions to dKP correspond to Z with a preferred section of

−1/4

(see [46]). Finally the solutions to the Diff(S

) equation correspond to Z

which holomorphically ﬁbre over CP

(see [51]).

If the Killing vector is null then the induced vector ﬁeld on the twistor space

PT vanishes on a hypersurface. This is because at each point, the Killing vector

284 10 : Anti-self-dual conformal structures

is tangent to a single α-surface. Hence it preserves a foliation by α-surfaces, and

vanishes at the hypersurface in twistor space corresponding to this foliation.

However, one can show [57] that it is possible to continue the vector ﬁeld on

twistor space to a one-dimensional distribution

K that is nowhere vanishing.

Quotienting PT by this distribution gives a two-dimensional complex mani-

fold Z containing CP

’s with normal bundle O (1), and we can make use of

another result of Hitchin:

Theorem 10.5.9 (Hitchin [79]) There is a one-to-one correspondence between

two-dimensional projective structures and two-dimensional complex mani-

folds admitting a two- parameter family of rational curves with normal bundle

O(1).

In this correspondence the points of the projective structure U correspond to

rational curves in a complex surface Z, and the geodesics of the projective

structure correspond to points in Z. Two points in U are connected by a

geodesic iff the corresponding rational curves in Z intersect at one point.

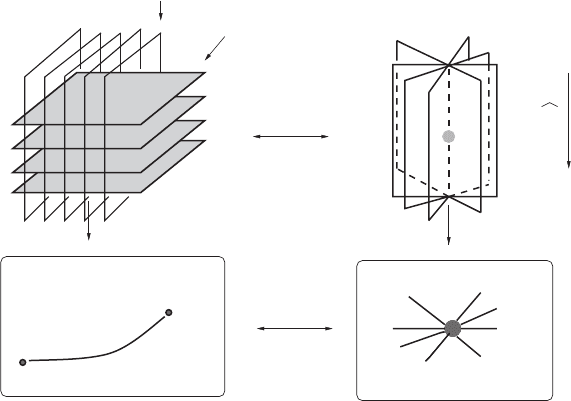
The twistorial version of the correspondence described in Section 10.3.2 is

illustrated by the Figure 10.2. In M, a one parameter family of β-surfaces

is shown, each of which intersects a one-parameter family of α-surfaces s,

also shown. The β-surfaces correspond to a projective structure geodesic in U,

shown at the bottom left.

‚1

‚2

‚1

‚2

‚1

‚2

„

‚1

‚2

· surface

‚ surface

Figure 10.2 Relationship between M, U, PT ,andZ

10.5 Twistor theory 285

The β-surfaces in M correspond to surfaces in PT . These surfaces intersect

at the dotted line, which corresponds to the one-parameter family of α-surfaces

in M. When we quotient PT by

K to get Z, the surfaces become twistor lines

in Z, and the dotted line becomes a point at which the twistor lines intersect,

this is shown on the bottom right. This family of twistor lines intersecting at a

point corresponds to the geodesic of the projective structure. See [29, 57] for

the details of this correspondence.

Exercises

1. Show that the curvature scalar of a four-dimensional null-Kähler structure

vanishes. [Hint: Differentiate the relation ∇



= 0 where ι



is the parallel

spinor deﬁning the null-Kähler structure.]

Impose the ASD Ricci-ﬂat condition on the null-Kähler structure

(10.2.13) and show that the function satisﬁes the second heavenly equa-

tion (10.2.22).

Calculate the ASD Weyl spinor C

ABC D

of (10.2.13) in terms of and

deduce that SD null-Kähler structures are given by (10.2.13) with =

ABC

where x

=(x, y) and !

ABC

are arbitrary functions of (w, z).

2. Show that the vector ﬁelds

= −x

∂

∂x

,τ

−

∂

∂x

, and τ

=2x

∂

∂x

generate the Lie algebra sl(2, R). Use the KdV Lax pair (8.1.2) with the

matrices replaced by vector ﬁelds to obtain solutions to the Diff(S

) equa-

tion (10.3.53) out of solutions to the KdV.

[Hint: Proceed by analogy with the procedure leading to (10.3.59).]

3. Show that all solutions to the Laplace equation in R



i=1

∂

∂x

which are constant on central quadrics are of the form

V =





(H − β

)(H − β

) ···(H − β

)

where



i=1

H − β

= C,

and C,β

,β

,...,β

are constants.