Dunajski M. Solitons, Instantons, and Twistors
Подождите немного. Документ загружается.


286 10 : Anti-self-dual conformal structures
4. Consider a deformation of the twistor space given by a Hamiltonian f =
f (ω
0
,π
A
) homogeneous of degree two and independent of ω
1
, and show
that it leads to a family of ASD pp-waves generalizing the metric (10.5.116)
and given by
g = dwdx + dzdy + F (w, y)dw
2
,
where F is an arbitrary function of two variables.
5. Find the ASD Ricci-flat metric corresponding to a deformed twistor space
with a deformation Hamiltonian
f =
(π
0
)
4
ω
0
ω
1
.
[Hint: Show that the deformation equations integrate to
˜ω
0
= exp[t(π
0
)
4
Q
−2
]ω
0
and ˜ω
1
= exp [−t(π
0
)
4
Q
−2
]ω
1
, (10.5.129)
where Q = ω
0
ω
1
restricts to α
A
β
B
π
A
π
B
on each twistor curve for some α
A
and β
A
. Obtain the splitting Q
−2
(o ·π)
4
=
˜
h − h where, setting ∂
α
:= o
A
∂
∂α
A
and ∂
β
:= o
A
∂
∂β
A
,
˜
h =2(π · o)∂
α
∂
β
α · o
(α · β)(π · α)
and h =2(π · o)∂
α
∂
β
β · o
(α · β)(π · β)
.
The twistor curves are now given by
ω
0
=(γ · π )e
ht
and ω
1
=(δ · π )e
−ht
,
for some spinors γ
A
and δ
A
.]
APPENDIX A
Manifolds and Topology
The first six chapters of this book are intended to give an elementary introduction
to the subject and the reader is expected only to be familiar with basic real and
complex analysis, algebra, and dynamics as covered in the undergraduate syllabus.
In particular no knowledge of differential geometry is assumed. One obvious
advantage of this approach is that the book is suitable for advanced undergraduate
students.
The disadvantage is that the discussion of Hamiltonian formalism and con-
tinuous groups of transformations in earlier chapters used phrases like ‘spaces
coordinatized by ( p, q)’, ‘open sets in
R
n
’, or ‘groups whose elements smoothly
depend on parameters’ instead calling these object by their real name – manifolds.
The first part of this appendix is intended to fill this gap. The second part of
the appendix contains the discussion of homotopy groups and topological degree
needed in Chapters 5–7.
Definition A.0.1 An n-dimensional smooth manifold is a set M together with a
collection of open sets U
α
called the coordinate charts such that
r
The open sets U
α
labelled by a countable index α cover M.
r
There exist one-to-one maps φ
α
: U
α
→ V
α
onto open sets in R
n
such that for any
pair of overlapping coordinate charts the maps
φ
β
◦ φ
−1
α
: φ
α
(U
α
∩ U
β
) −→ φ
β
(U
α
∩ U
β
)
are smooth (i.e. infinitely differentiable) functions from
R
n
to R
n
. (Figure A.1)
Thus a manifold is a topological space together with additional structure which
makes local differential calculus possible. The space
R
n
itself is of course a manifold
which can be covered by one coordinate chart.
r
Example. A less trivial example is the unit sphere
S
n
= {r ∈ R
n+1
, |r| =1}.
To verify that this is indeed a manifold, cover S
n
by two open sets U
1
= U and
U
2
=
U:
U = S
n
/{0,...,0, 1} and
U = S
n
/{0,...,0, −1},
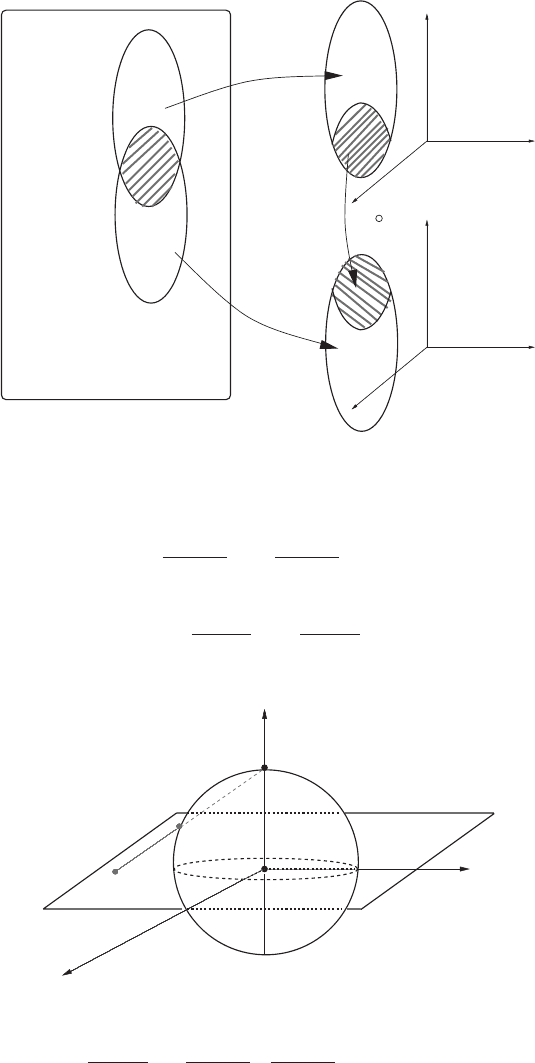
288 A: Manifolds and topology
U
·
R
n
R
n
U
‚
V
·
V
‚
M
÷
·
÷
‚
÷
‚
÷
·
–1
Figure A.1 Manifold
and define the local coordinates by stereographic projections
φ(r
1
, r
2
,...,r
n+1
)=
r
1
1 − r
n+1
,...,
r
n
1 − r
n+1
=(x
1
,...,x
n
) ∈ R
n
and
˜
φ(r
1
, r
2
,...,r
n+1
)=
r
1
1+r
n+1
,...,
r
n
1+r
n+1
=(x
1
,...,x
n
) ∈ R
n
.
N = (0, 0, . . . , 0, 1)
r
n+1
R
n
P
ê (P)
Using
r
k
1+r
n+1
=
1 − r
n+1
1+r
n+1
r
k
1 − r
n+1
, k =1,...,n,

289
where r
n+1
= ±1 shows that on the overlap U ∩
U the transition functions
φ ◦
˜
φ
−1
(x
1
,...,x
n
)=
x
1
x
2
1
+ ···+ x
2
n
,...,
x
n
x
2
1
+ ···+ x
2
n
are smooth.
The Cartesian product of manifolds is also a manifold. For example, the n-torus
arising in the Arnold–Liouville theorem (Theorem 1.2.2) is the Cartesian product
of n one-dimensional spheres.
Another way to obtain interesting manifolds is to define them as surfaces in
R
n
by a vanishing condition for a set of functions. If f
1
,..., f
k
: R
n
→ R then the set
M
f
:= (x ∈ R
n
, f
i
(x)=0, i =1,...,k) (A1)
is a manifold if the rank of the k × n matrix of gradients ∇ f
i
is constant in a
neighborhood of M
f
in R
n
. If this rank is maximal and equal to k then dim M
f
=
n − k. The manifold axioms can be verified using the implicit function theorem. For
example, the sphere S
n−1
arises this way with k = 1 and f
1
=1−|x|
2
.Thereisa
theorem which says that every manifold arises as some surface in
R
n
for sufficiently
large n. If the manifold is m-dimensional then n is at most 2m + 1. This useful
theorem is now nearly forgotten – differential geometers like to think of manifolds
as abstract objects defined by a collections of charts as in Definition A.0.1.
A map between smooth manifolds f : M →
M, where dim M = n and dim
M =
˜
n, is called smooth if it is smooth in local coordinates. This means that the maps
˜
φ
β
◦ f ◦ φ
α
−1
: R
n
−→ R
˜
n
are smooth maps in the ordinary sense. Here (U
α
,φ
α
) and (
U
β
,
˜
φ
β
) are coordinate
charts for M and
M, respectively.
Let γ :
R → M be a smooth curve such that
γ (0) = p ∈ M and
dγ (ε)
dε
|
ε=0
= V ∈ T
p
M,
where V is a vector tangent to γ at p and the tangent space T
p
M consists of all
tangent vectors to all possible curves through p.IfdimM = n, the tangent space is
an n-dimensional vector space. The collection of all tangent spaces as p varies in
M is called the tangent bundle TM = ∪
p∈M
T
p
M. The tangent bundle is a manifold
of dimension 2n.
A smooth map f between two manifolds induces, for each p ∈ M, a smooth
map between tangent spaces
f
∗
: T
p
M −→ T
f ( p)
M
such that
f
∗
(V)=
df(γ (ε))
dε
|
ε=0
. (A2)
This map is called the tangent map. It depends smoothly on a point p ∈ M and
thus it extends to the tangent bundle TM.IfV
i
are components of the vector field

290 A: Manifolds and topology
V with respect to the natural basis {∂/∂x
i
} then
( f
∗
V)
i
= V
j
∂γ
i
∂x
j
.
The Lie derivative of a vector W along a vector V is defined as
Lie
V
W = lim
→0
W( p) − γ ()
∗
W( p)
, (A3)
where γ () is the one-parameter group of transformations generated by V. Thus,
using the Leibniz rule
Lie
V
( f )=V( f ), Lie
V
(W)=[V, W], and Lie
V
(ω)=d(V ω)+V
(dω),
where f, W, and ω are a function, a vector field and a one-form, respectivelly, and
is a contraction of a differential form with a vector field.
A.1 Lie groups
We can now give a proper definition of a Lie group:
Definition A.1.1 A Lie group G is a group and, at the same time, a smooth
manifold such that the group operations
G × G → G, (g
1
, g
2
) → g
1
g
2
, and G → G, g → g
−1
are smooth maps between manifolds.
r
Example. The general linear group G = GL(n, R) is an open set in R
n
2
defined
by the condition det g =0, g ∈ G. It is therefore a Lie group of dimension n
2
.
The special orthogonal group SO(n) is defined by (A1), where the n(n +1)/2
conditions in
R
n
2
are
gg
T
− 1 =0, det g =1.
The determinant condition just selects a connected component in the set of
orthogonal matrices, so it does not count as a separate condition. It can be shown
that the corresponding matrix of gradients has constant rank and thus SO(n)is
an [n(n − 1)/2]-dimensional Lie group.
In Chapter 4 a Lie algebra
g was defined as a vector space with an antisymmetric
bilinear operation which satisfies the Jacobi identity (4.2.6).
A Lie algebra of a Lie group G is the tangent space to G at the identity element,
g = T
e
G with the Lie bracket defined by a commutator of vector fields at e. For any
g ∈ G define left translation L
g
using the group multiplication
L
g
: G −→ G and L
g
(h)=gh.
The tangent mapping (A2) maps T
e
G = g to T
g
G and each element V ∈ g corre-
sponds to a vector field (L
g
)
∗
V on the group manifold. Theses vector fields are
A.1 Lie groups 291
called left-invariant. The Lie bracket of two left-invartiant vector fields is again
left-invariant as
[(L
g
)
∗
(V), (L
g
)
∗
(W)] = (L
g
)
∗
[V, W]
g
from the properties of the tangent map (A2). (The bracket on the LHS is the Lie
bracket of two vector fields. The symbol [ , ]
g
on the RHS is the bracket in the Lie
algebra
g.) Therefore the elements of g can be represented by global vector fields
on G, and Lie groups are paralizable as they globally admit dim(G) non-vanishing
vector fields which are left translations of vectors in
g.
Let L
α
,α =1,...,dimg be a basis of left-invariant vector fields such that
[L
α
, L
β
]= f
γ
αβ
L
γ
,
and let σ
α
be the dual basis of one-forms such that L
α
σ
β
= δ
β
α
. The identity
dω(V, W)=V[ω(W)] − W[ω(V)] − ω([V, W])
with V = L
α
, W = L
β
, and ω = σ
γ
gives
dσ
α
+
1
2
f
α
βγ
σ
β
∧ σ
γ
=0.
If G is a matrix group the one-form
g
−1
dg
is called the Maurer–Cartan one-from on G. The Maurer–Cartan one-form is
invariant under left multiplication of g by a constant group element. This one-
form takes its values in
g, as for any smooth curve g(s)inG we have
g
−1
(s)g(s + ε)=1+εg
−1
dg
ds
|
ε=0
+ O(ε
2
),
so g
−1
(dg/ds) is a tangent vector to G at g, and so it is an element of g. Thus we
can write
g
−1
dg = σ
α
T
α
,
where T
α
are matrices spanning g and σ
α
are left-invariant one-forms on G. The
metric
h = −Tr(g
−1
dg g
−1
dg)=−Tr(T
α
T
β
)σ
α
σ
β
is the left-invariant metric on the Lie group.
The right-invariant one-forms ˜σ
α
are defined by
g
−1
dg = T
α
˜σ
α
,
and the right-invariant vector fields R
α
are defined by the duality R
α
˜σ
β
= δ
β
α
.
They satisfy
[R
α
, L
β
]=0 and [R
α
, R
β
]=− f
γ
αβ
R
γ
.

292 A: Manifolds and topology
r
Example. The left-invariant one-forms σ
α
on the Lie group SO(3) can be
explicitly given in terms of Euler angles:
σ
1
= cos ψ dθ + sin ψ sin θ dφ, σ
2
= −sin ψ dθ + cos ψ sin θ dφ, and
σ
3
= dψ + cos θ dφ.
r
Example. Consider the three-dimensional Heisenberg group (4.1.1) with the
corresponding Lie algebra (4.1.3). We have
g
−1
=
⎛
⎜
⎝
1 −m
1
−m
3
+ m
1
m
2
01 −m
2
00 1
⎞
⎟
⎠
so
g
−1
dg = T
α
σ
α
= T
1
dm
1
+ T
2
dm
2
+ T
3
(dm
3
− m
1
dm
2
).
This gives
dσ
1
=0, dσ
2
=0, and dσ
3
= −σ
1
∧ σ
2
.
The left-invariant metric
h =(σ
1
)
2
+(σ
2
)
2
+(σ
3
)
2
= dm
2
1
+ dm
2
2
+(dm
3
− m
1
dm
2
)
2
has a Kaluza–Klein interpretation: Its geodesics, when projected to the (m
1
, m
2
)-
plane, are trajectories of a particle moving in a uniform magnetic field F = dm
1
∧
dm
2
with a potential A = m
1
dm
2
. The first integral
˙
m
3
− m
1
˙
m
2
= const of the
geodesic motion corresponds to charge conservation.
If G is a transformation group of some manifold X, then the elements of
g can
also be represented by vector fields on X.Ifρ : G × X −→ X then for any V ∈
g
we define ρ(V) to be a vector in X by demanding that its flow coincides with a
one-parameter subgroup e
εV
of G in X. This induces a Lie algebra homomorphism
form
g to the Lie algebra of vector fields on X, that is,
[ρ(V),ρ(W)] = ρ([V, W]
g
), V, W ∈ g.
We will usually omit the reference to the map ρ, and denote the vectors in
g and
the corresponding vector fields in TXby the same symbol.
r
Example. The group SO(3, R) acts on R
3
as the group of rotations. The action
x −→ Ax is infinitesimaly generated by three vector fields
X
c
=
1
2
ε
abc
x
a
∂
∂x
b
.
The group preserves the Euclidean distance, and so its action descends to the
two-sphere S
2
⊂ R
3
given by |x| = 1. The S
2
-volume form ω = d(cos θ ) ∧ dψ is

A.1 Lie groups 293
preserved by this action, and the corresponding vector fields are Hamiltonian,
that is, X
c
ω = −dh
c
with Hamiltonians h
a
: S
2
−→ R:
h
1
= sin θ sin ψ, h
2
= −sin θ cos ψ, and h
3
= cos θ
such that
{h
a
, h
b
} =
1
2
ε
abc
h
c
. (A4)
Proof of the first part of Arnold–Liouville’s Theorem 1.2.2. The gradients ∇ f
k
are
independent, thus the set
M
f
:= {(p, q) ∈ M; f
k
(p, q)=c
k
},
where c
1
, c
2
,...,c
n
are constant defines a manifold of dimension n.Letξ
a
=(p, q)
be local coordinates on M such that the Poisson bracket is
{ f, g} = ω
ab
∂ f
∂ξ
a
∂g
∂ξ
b
, a, b =1, 2,...,2n,
where ω is the constant antisymmetric matrix
01
n
−1
n
0
.
The vanishing of the Poisson brackets { f
j
, f
k
} = 0 implies that each Hamiltonian
vector field
X
f
k
= ω
ab
∂ f
k
∂ξ
b
∂
∂ξ
a
is orthogonal (in the Euclidean sense) to any of the gradients ∂
a
f
j
, a =
1,...,2n, j, k =1,...,n. The gradients are perpendicular to M
f
, thus the Hamil-
tonian vector fields are tangent to M
f
. They are also commuting as
[X
f
j
, X
f
k
]=−X
{ f
j
, f
k
}
=0,
so the vectors generate an action of the abelian group
R
n
on M. This action restricts
to an
R
n
action on M
f
. Let p
0
∈ M
f
, and let be the lattice consisting of all vectors
in
R
n
which fix p
0
under the group action. Then is a discrete subgroup of R
n
and
(by an intuitively clear modification of the orbit-stabiliser theorem) we have
M
f
= R
n
/.
Assuming that M
f
is compact, this quotient space is diffeomorphic to a torus T
n
.
In fact this argument shows that we get a torus for any choice of the constants
c
k
. Thus, varying the constants, we find that the phase-space M is foliated by
n-dimensional tori.

294 A: Manifolds and topology
A.2 Degree of a map and homotopy
Definition A.2.1 Let M
1
and M
2
be oriented, compact D-dimensional manifolds
without boundary, and let ω be a volume-form on M
2
. A degree deg( f ) of a smooth
map f : M
1
→ M
2
is given by
M
1
f
∗
ω =[deg( f )]
M
2
ω. (A5)
Rescaling ω by a constant does not change the degree, and neither does choosing a
different volume-form because
M
2
ω =
M
2
ω
implies that ω − ω
= dα for some (D − 1)-form α (the D-dimensional cohomology
of M
2
is one-dimensional) and
f
∗
ω
= f
∗
ω − f
∗
dα = f
∗
ω − d( f
∗
α)
gives
M
1
( f
∗
ω
− f
∗
ω)=0
by application of Stokes’ theorem. We conclude that the deg( f ) depends only
on f .
There is another useful way of calculating degree by counting a number of pre-
images. Let y ∈ M
2
be a generic point, that is, the set f
−1
(y)={x; f (x)=y} is
finite, and the Jacobian J ( f ) = 0 (recall that if x ∈ U has local coordinates x
i
, and
y ∈ f (U) has local coordinates y
i
, then J = det (∂ y
i
/∂x
j
)ify
i
= y
i
(x
1
,...,x
D
)).
Proposition A.2.2 deg( f ) is the integer given by
deg( f )=
x∈f
−1
(y)
sign[J (x)]. (A6)
Proof Let f
−1
(y)={x
α
}, where α is a discrete index with possibly infinite range.
The set of critical values of f has measure zero (by the Sard theorem [43]), and
such points do not contribute to the integral. Clearly (A6) is an integer, but it may
depend on the choice of y. Choose a neighbourhood V of y and U
α
of x
α
for some
fixed value of α such that f : U
α
→ V is one-to-one and onto. Let ω have support
on
-
f (U
α
) ⊂ V (i.e. ω = 0 outside V). Therefore
M
1
f
∗
(ω)=
α
U
α
f
∗
ω.
Now change coordinates from x
j
to y
j
near x
α
. Then
U
1
f
∗
ω =
V
ω
sign[J (x
α
)],
A.2 Degree of a map and homotopy 295
where we have used
ω = ρ(y)dy
1
∧···∧dy
D
and
f
∗
ω =
ρ[ f (x)]Jdx
1
∧···∧dx
D
=
ρ(y)dy
1
∧···∧dy
D
sign(J )
as the last change of variables from x to y introduces the term |J |
−1
. We obtain
similar relations on all other open sets U
α
, which proves (A6).
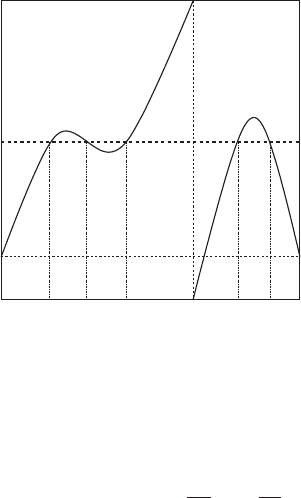
r
Example. f : S
1
→ S
1
. In this case the topological degree is called the winding
number. Formula (A6) gives
N =
θ: f (θ )= f
0
sign(df/dθ ).
If the graph of f looks like
2
f(Ë)
f
0
2π
+ ++−−
Ë
1
Ë
2
Ë
3
Ë
4
Ë
5
then applying (A6) we find
N =1− 1+1+1− 1=1.
Alternatively the degree can be calculated from the definition (A5) which yields
N = (vol
S
1
)
−1
S
1
df =
1
2π
2π
0
df
dθ
dθ.
If we think of S
1
as the unit circle |z| = 1 in the complex plane then every map of
degree k is homotopic to f (z)=z
k
.
r
Example. For any k ∈ Z there exist smooth maps from S
n
to S
n
of degree k. Let
f : S
n−1
−→ S
n−1
be a smooth map which takes a unit vector n in R
n
to another
such vector f (n). We can construct the suspension f : S
n
−→ S
n
of f by the
