Дубровский В.Г. Теоретические основы технологии полупроводниковых наноструктур
Подождите немного. Документ загружается.


Для выполнения первого граничного условия (1.32) необходимо, чтобы скорость
нуклеации была равна
1
0
)](exp[
)(
−
∞
+
⎥
⎦
⎤
⎢
⎣
⎡
∆=
∫
iF
iW
di
nI
(1.34)
Чрезвычайно резкий максимум подинтегральной функции в (1.34) при i=i
c
позволяет
вычислить интеграл методом Лапласа. В результате для I получим
)exp()(
2
/)(/
FiW
iF
nI
c
c
−
′′
∆
=
+
π
(1.35)
где выражение под квадратным корнем иногда называют неравновесным фактором
Зельдовича. Для рассматриваемого случая нуклеации двумерных островков на
поверхности функция W
+
(i) имеет вид, аналогичный (1.22)
2/1
)( ni
t
l
iW
D
D
σ
=
+
(1.36)
где длина ступени l должна быть заменена на периметр островка p
i
=4(
σ
i)
1/2
. Такая
аппроксимация справедлива для решеточной модели в случае сильно локализованной
адсорбции. Используя (1.27)-(1.29), (1.36) в (1.35), находим окончательное выражение для
скорости нуклеации двумерных островков
⎥
⎦
⎤
⎢
⎣
⎡
+
−++=
)1ln(
exp)1(ln)1(
1
2/1
ζ
ζζ
στπ
a
I
D
(1.37)
Здесь
τ
D
– характерное время роста островков, определяемое согласно
eq
D
Deq
D
D
t
ln
t
θ
σ
τ
~
2
=
(1.38)
Аналогичным образом можно получить скорость нуклеации трехмерных островков.
Результат будет иметь вид [2]
⎥
⎦
⎤
⎢
⎣
⎡
+
−
)1(ln
exp
1
~
2
ζ
στ
b
I
D
(1.39)
39
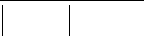
где ,
γ
- поверхностная энергия депозита,
φ
-
контактный угол. Формулы (1.37), (1.38) показывают, что при больших значениях
энергетических параметров a и b скорость нуклеации чрезвычайно резко зависит от
пересыщения адатомов. При относительно малом падении пересыщения I уменьшается на
порядок величины.
()
3/)cos1)(cos2(/16
23
3
φφσγ
−+= Tkb
B
Время установления стационарного режима нуклеации в прикритической области t
s
оценивалась в работах [52,55,58]:
)()(
1
~
cc
s
iWiF
t
+
′′
(1.40)
И для плоских, и для трехмерных островков это время очень мало - не более 10
-4
-10
-5
сек.
Поэтому для практических расчетов вполне достаточно знать только скорость нуклеации,
считая, что стационарное состояние мгновенно охватывает всю прикритическую область.
Условием применимости классической теории нуклеации является сильное
неравенство [52,59]
1)exp( >>F
(1.41)
Это условие физически означает малость флуктуаций в прикритической области, которая
обеспечивается большой высотой активационного барьера зародышеобразования.
I.6 Независимый рост островков
В закритической области диффузия в пространстве размеров, описываемая
вторыми производными в уравнении Зельдовича, становится несущественна, так как все
закритические островки растут уже устойчиво. В результате функция распределения
закритических островков
по размерам подчиняется уравнению первого порядка. В этом
уравнении удобно выбрать такую переменную, связанную с размером островков, в
терминах которой скорость латерального роста островково не зависит от их размера, а
зависит только от времени [24]. Если скорость присоединения адатомов к островку
40

пропорциональна его периметру, то из (1.36) с учетом определения для
τ
D
(1.38) следует
выражение для скорости роста закритических островков
ζ
τ
2/1
2
i
dt
di
D
=
(1.42)
Отсюда видно, что скорость роста не зависит от размера островка для переменной
ρσσ
≡= ir
; (1.43)
2/1
i=
ρ
Здесь r есть длина стороны квадратного островка,
ρ
- размер островка, выраженный в
единицах постоянной решетки. Для него из (1.42) получаем
D
t
dt
d
τ
ζ
ρ
)(
=
(1.44)
Таким образом, в терминах переменной
ρ
скорость роста закритических островков
пропорциональна пересыщению адатомов с характерным временем латерального роста
τ
D
.
В случае механизма латерального роста, отличного от (1.42), всегда можно выбрать такую
переменную
ρ
, для которой скорость роста не зависит от
ρ
. Например, если di/dt~i
m
, то
ρ
=i
1-m
.
Уравнение для функции распределения закритических островков по размерам f(
ρ
,t)
имеет вид [2]
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=====
∂
∂
=
∂
∂
)(
))((
)(),0(;0),(
t
tI
tftfotf
f
t
f
D
s
D
ζ
ζτ
ρρ
ρτ
ζ
(1.45)
Начальное условие к (1.45) очевидно: мы считаем, что в момент времени t=0 на
поверхности нет островков. Граничное условие к (1.45), вообще говоря, должно ставиться
на границе прикритической и закритической областей [24]. Однако, поскольку
критический размер зародыша всегда мал (порядка нескольких десятков атомов), при
рассмотрении роста закритических островков его можно положить равным нулю.
41

Стационарная функция распределения при
ρ
=0 равна
τ
D
I/
ζ
. Это означает, что зародыши,
рождающиеся с интенсивностью I, проходят через прикритическую область со скоростью
d
ρ
/dt=
ζ
/
τ
D
. Решением уравнения (1.45) является функция распределения
(
))((),(
*
)
ρ
ρ
ζ
ρ
−= tftf
s
(1.46)
Здесь
ρ
*
(t) – функция времени, полученная интегрированием уравнения (1.44). Начальное
условие для
ρ
*
(t) естественно выбрать следующим образом [60]: размер
ρ
*
равен нулю в
точке максимума пересыщения, когда островки зарождаются с максимальной
интенсивностью. Это определение означает, что
ρ
*
(t) описывает рост во времени наиболее
представительного («среднего») размера островков, соответствующего максимуму
функции распределения по размерам:
∫
′′
=
t
t
D
ttdt
*
)(
1
)(
*
ζ
τ
ρ
(1.47)
Решение (1.46) позволяет утверждать, что функция распределения по размерам не меняет
своей формы во времени и как единое целое перемещается по оси размеров
ρ
с
постоянной для всех островков скоростью
ζ
(t)/
τ
D
, зависящей только от времени. Именно
для этого и была введена переменная
ρ
, для которой скорость роста не зависит от размера
островка. Следовательно, все характеристики функции распределения по размерам
(поверхностная плотность, дисперсия по размерам и т.д.) определяются на стадии
нуклеации, а уравнение (1.47) определяет закон движения спектра островков по размерам
по оси размеров как целого как целого.
Эволюция во времени среднего размера
и распределения по размерам целиком
определяется зависимостью от времени пересыщения адатомов. Для того, чтобы найти эту
зависимость, необходимо привлечь уравнение материального баланса на поверхности
подложки. На начальном этапе роста, когда степень заполнения поверхности островками
мала, это уравнение имеет вид
42

∫
+=
⎥
⎦
⎤
⎢
⎣
⎡
′
−
′
t
ISL
A
tntn
tn
Jtd
0
)()(
)(
τ
(1.48)
Правая часть (1.48) дает общее количество атомов, поступивших на единицу площади
поверхности за время t с момента начала осаждения. Оно равно сумме концентрации
адатомов в момент времени t n(t) и числу атомов, находящихся в составе островков на
единице площади поверхности n
ISL
(t). Последнюю величину можно выразить как через
функцию распределения островков по размерам, так и через интенсивность зарождения и
скорость роста островков:
∫∫∫
∞
′
⎥
⎦
⎤
⎢
⎣
⎡
′′
′′′′
==
0
2
0
2
)(
)(),()(
t
t
D
t
ISL
t
tdtItdtfdtn
τ
ζ
ρρρ
(1.49)
Эквивалентность двух форм записи (1.49) следует из (1.44) и (1.45). В терминах
пересыщения адатомов (1.49) примет вид
)()(1)]([
1
0
max
tGtttd
t
A
+=−
′
−Φ
′
∫
ζζ
τ
(1.50)
Здесь G(t) – число атомов в островках, выраженное в единицах равновесной концентрации
адатомов
eq
ISL
n
tn
tG
)(
)( =
(1.51)
Величина
Φ
max
по физическому смыслу равна максимальному идеальному пересыщению
адатомов, которое установилось бы на поверхности в отсутствие зарождения островков
(приводим различные варианты записи
Φ
max
):
1exp11
max
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Λ+
=−=−≡Φ
Tk
E
V
V
n
J
B
A
Aeq
A
eq
A
νθ
ττ
(1.52)
Здесь учтены приведенные ранее формулы для равновесной плотности адатомов n
eq
,
времени жизни адатома на поверхности
τ
A
и скрытой теплоты конденсации Λ.
43
Максимальное идеальное пересыщение является важнейшим управляющим параметром
ростового процесса. Согласно (1.52), для данной системы материалов оно определяется
температурой поверхности T и скоростью осаждения V.
На стадии независимого роста островков степень заполнения ими подложки g(t)
равна
)()()( tGtntg
eqISL
θ
σ
==
(1.53)
Это выражение справедливо только при малых g(t). Слияние островков наступает тогда,
когда g(t) возрастает до величины, сравнимой с единицей.
I.7. Оствальдовское созревание
Стадия оствальдовского созревания является поздней стадией фазового перехода. В
случае тонких пленок она имеет место только при достаточно слабых источниках
осаждения или в режимах с остановкой роста. Физическая сущность процесса
заключается в следующем. На стадии независимого роста островков пересыщение
адатомов уменьшается до нуля, поскольку островки растут именно за счет потребления
адатомов с поверхности. Для достаточно больших островков может происходить смена
режима роста, то есть скорость роста островков может отличаться от (1.44). Новых
островков при этом больше не рождается. Сформированный
на стадии нуклеации спектр
островков по размерам движется вправо по оси размеров, однако начинает возрастать и
критический размер i
c
, определяемый формулой (1.28). Согласно этой формуле, при
ζ
→0
критический размер стремиться к бесконечности. Это означает, что на некотором этапе
роста критический размер может догнать перемещающийся по оси размеров спектр
островков (Рис.7). Поскольку островки докритического размера распадаются, а
закритического – растут, на данном этапе в системе возникает особого рода
взаимодействие, передающиеся через обобщенное диффузионное поле. Оно приводит к
тому, что
большие островки начинают расти за счет распада меньших. Этот процесс и
44
называется Отсвальдовским созреванием. Для того, чтобы стадия оствальдовского
созревания наблюдалась, в случае сингулярной поверхности необходимо, чтобы
поверхностная плотность островков N и их средний размер r
*
по окончании стадии
независимого роста (когда
ζ
→0) удовлетворяли неравенствам [61]
2
*
2
*
][
−
−
<<+ rNr
λ
(1.54)
где L
D
– диффузионная длина адатома (1.21). Если N>r
*
-2
, то островки сольются раньше,
чем наступит стадия Оствальдовского созревания. Если, напротив, N<[r
*
+L
D
]
-2
, то атомы
десорбируются с поверхности и не смогут участвовать в диффузионном процессе.
Поскольку в дальнейшем будут в основном рассматриваться вопросы, связанные с
эпитаксиальным выращиванием тонких пленок и наноструктур, для которого типичны
большие скорости осаждения и высокие плотности островков, нас обычно не будет
интересовать стадия Оствальдовского созревания. В рассматриваемых ниже
задачах
определенный тип взаимодействия между островками (прямое слияние, упругое
взаимодействие, передаваемое через подложку и т.п.) всегда наступает раньше, чем стадия
r
c
(0)
v
c
v
r
c
(t)
Island size, r
Size distribution, f(r,t)
Рис.7. Схематическое
изображение процесса
Оствальдовского созревания.
Если скорость роста
островков v меньше
скорости роста критического
размера v
c
, то он догонит
движущийся вправо по оси
размеров спектр. При этом
все островки размера r<r
c
испаряться, а островки с r>r
c
вырастут.
45
Оствальдовского созревания, то есть осуществляется режим с N>r
*
-2
. Поэтому здесь лишь
отметим, что основная идея анализа этой стадии восходит к работе Лифшица и Слезова
[62], которые получили автомодельное решение для функции распределения островков по
размерам на стадии Оствальдовского созревания. Полученные в [62] результаты имеют
весьма общий характер и применимы ко всем дисперсным системам, состоящим из
островков новой фазы и
атомов старой фазы. Именно поэтому указанную стадию иногда
называют переконденсацией Лифшица-Слезова. Современное состояние теории
Оствальдовского созревания на поверхности твердого тела подробно изложено в
монографиях [61] и [63]. Наиболее полное теоретическое описание процесса
Оствальдовского созревания проведено в работе [64], где было получено асимптотическое
решение для функции распределения по размерам, уточняющее результаты [62].
ЛЕКЦИЯ №4.
Формирование сплошной пленки
I.8. Слияние островков. Модель Колмогорова.
После завершения стадии независимого роста островков начинается их слияние
(иначе - коалесценция), в результате которого на поверхности и образуется сплошная
пленка. Вначале процесс коалесценции носит характер парного столкновения островков,
затем, по мере увеличения степени заполнения, начинают происходить множественные
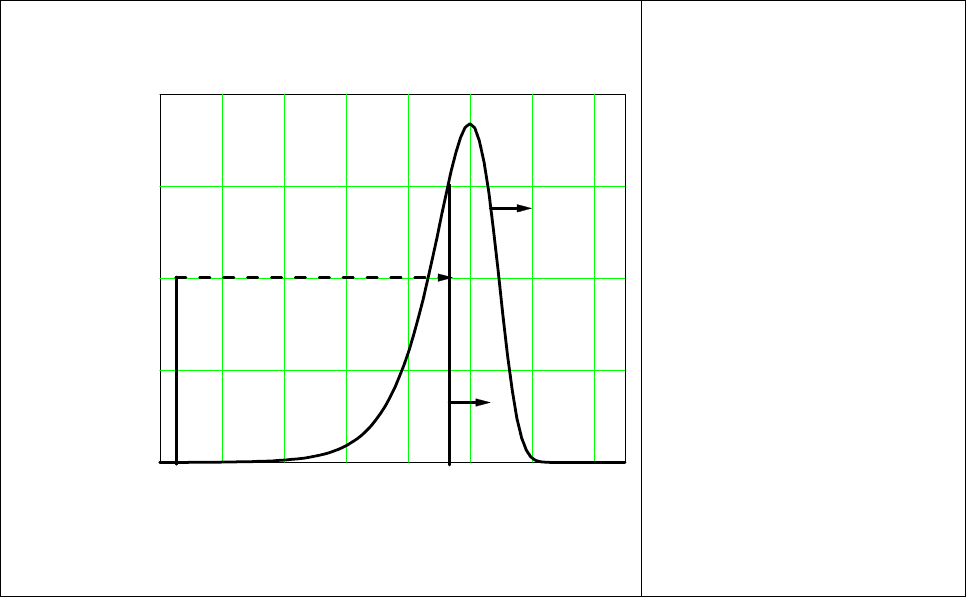
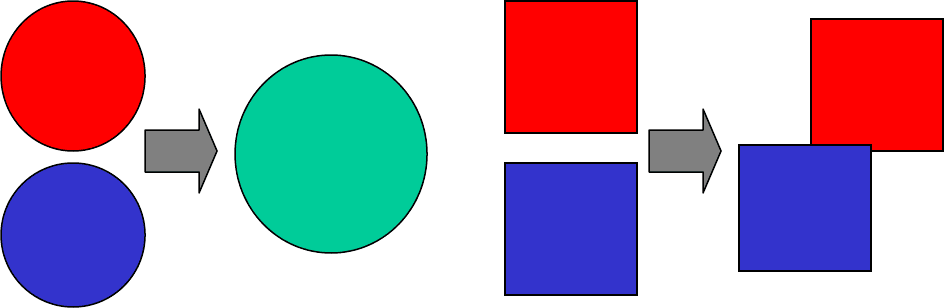
1 2
Рис.8. Жидкокапельная (1) и
твердофазная (2) коалесценция островков
46
столкновения трех, четырех и т.д. островков. На Рис.8 изображены два основных
механизма коалесценции: жидкокапельная и твердофазная [65]. В случае жидкокапельной
коалесценции сливающиеся островки ведут себя подобно каплям жидкости, то есть из
двух маленьких островков образуется один островок большего размера, но той же формы,
что и маленькие. В случае твердофазной
коалесценции сливающиеся островки ведут себя
подобно кристаллам, то есть при соприкосновении островков их рост в местах
соприкосновения прекращается, а в других местах продолжается прежним образом.
Жидкокапельная коалесценция двумерных островков за счет их бокового роста была
исследована Осиповым [66] в рамках кинетической модели для функции распределения
островков по размерам, где парная коалесценция описывается
моделью Смолуховского
[67]. В работе [66] вычислены основные характеристики ансамбля островков на стадии
коалесценции, в частности функция распределения островков по размерам, поверхностная
плотность и степень заполнения подложки островками. Было показано, что в результате
коалесценции плотность островков достигает максимума при некотором значении степени
заполнения. В частности, при постоянном ядре коагуляции этот максимум достигается
при заполнении, примерно равном 0.38.
При росте тонких пленок методом молекулярно-пучковой эпитаксии и его
разновидностями в подавляющем большинстве случаев наблюдается твердофазный
механизм коалесценции. Для теоретического исследования твердофазной коалесценции
широко используется геометрико – вероятностная модель Колмогорова [68]. В
иностранной литературе эту модель иногда называют моделью Колмогорова - Аврами или
Колмогорова – Джонсона – Мейла - Аврами (KJMA), по
имени ученых, получивших
аналогичные результаты несколько позднее [69,70] (о любопытной истории модели см.
[71], там же можно найти подробное изложение теории Колмогорова и ее приложений).
Применением модели Колмогорова для исследования кинетики ростовых процессов
47
занимались Кащиев [36,72] Беленький [71,73] Трофимов и Осадченко [74,75] и ряд других
авторов [25,76-78]. Теория кристаллизации Колмогорова справедлива в рамках
следующих предположений:
1) Зародыши кристалла возникают с одинаковой вероятностью во всех точках
системы, свободных от кристалла, с интенсивностью I(t), зависящей только от
времени; рождающиеся зародыши имеют нулевой размер.
2) Все зародыши имеют одинаковую форму
и ориентацию.
3) Скорость роста зародышей в терминах их линейного размера r зависит только от
времени и не зависит от размера зародыша: v=dr/dt =v(t).
4) Пренебрегается влиянием границ.
Функции I(t) и v(t) являются внешними функциями модели, то есть в рамках самой модели
никак не определяются.
В двумерном случае площадь зародыша есть
cr
2
, где r – линейный размер (радиус)
зародыша, с – константа формы. Формула Колмогорова для степени заполнения
поверхности двумерной пленкой в момент времени t Z(t) имеет вид
)](exp[1),()(exp1)(
0
2
tgtrIdctZ
t
−−≡
⎥
⎦
⎤
⎢
⎣
⎡
−−=
∫
τττ
(1.55)
Здесь
(1.56)
∫
′′
=
t
tvtdtr
τ
τ
)(),(
есть текущий линейный размер зародыша, родившегося в момент времени
τ
. В формулу
(1.55) входит функция g(t) – степень заполнения поверхности островками в отсутствие
коалесценции, то есть если все сросшиеся островки вновь раздвинуть. Поскольку в п. 1.6
мы устремили критический размер зародыша к нулю, интенсивность зарождения в модели
Колмогорова в точности равна интенсивности нуклеации, определяемой формулой (1.37).
Константа формы c для квадратных островков равна 1. Далее
, для скорости роста v(t) из
48
