Дубровский В.Г. Теоретические основы технологии полупроводниковых наноструктур
Подождите немного. Документ загружается.


[]
(
i
A
j
iijjji
D
i
b
tdt
d
θθ
τ
ϕθθθϕθθθ
)
θ
−++−−−−−=
∑
0
)1(
1
]exp[)1(]exp[)1(
4
1
(1.87)
Здесь
ϕ
- константа взаимодействия, t
D
– диффузионное время адатома,
τ
A
– время жизни
адатома на поверхности, эти параметры имеют тот же смысл, что и в выражениях (1.4),
(1.17), (1.20) соответственно. Величина b
≡
J
στ
A
определяет пространственно-однородное
решение (1.87) ленгмюровского типа
θ
i
=
θ
0
=b/(1+b). Сумма по j в (1.87) ведется по
ближайшим соседям узла i. Эта сумма представляет собой нелинейный диффузионный
оператор, суммирующий вероятности диффузионных прыжков из узлов j в i и наоборот.
Множители (1-
θ
i
) учитывают запрет на нахождение более чем одного атома в одном узле:
при
θ
i
=1 вероятность прыжка в узел i равна нулю, так как он занят (отталкивание).
Множители exp[-
ϕθ
i
] учитывают притяжение между адатомами: чем больше заполнение
поверхности вблизи узла i, тем сложнее осуществить прыжок из этого узла, в
приближении среднего поля заполнение вблизи i заменяется его значением в самом узле i.
Диффузионный оператор в (1.87) линеаризуется в случае
θ
i
→
0 (разреженная система) и
ϕ→
0 (отсутствие притяжения). Уравнение (1.87) сохраняет среднее по поверхности
значение плотности адатомов
θ
0
. Континуальное приближение (1.87) получается
разложением
θ
j
в ряд по постоянной решетки a=
√σ
c удержанием членов первого и
второго порядка по a:
θθθθ
θ
−+∇∇=
∂
∂
0
])([D
t
(1.88)
где введены безразмерные координаты x,y
≡
X,Y/a
√Γ
,
Γ≡τ
A
/t
D
(1+b). Зависящий от
заполнения решетки коэффициент диффузии имеет вид
)exp()1()(
2
ϕθϕθϕθθ
−+−=D
(1.89)
Функция D(
θ
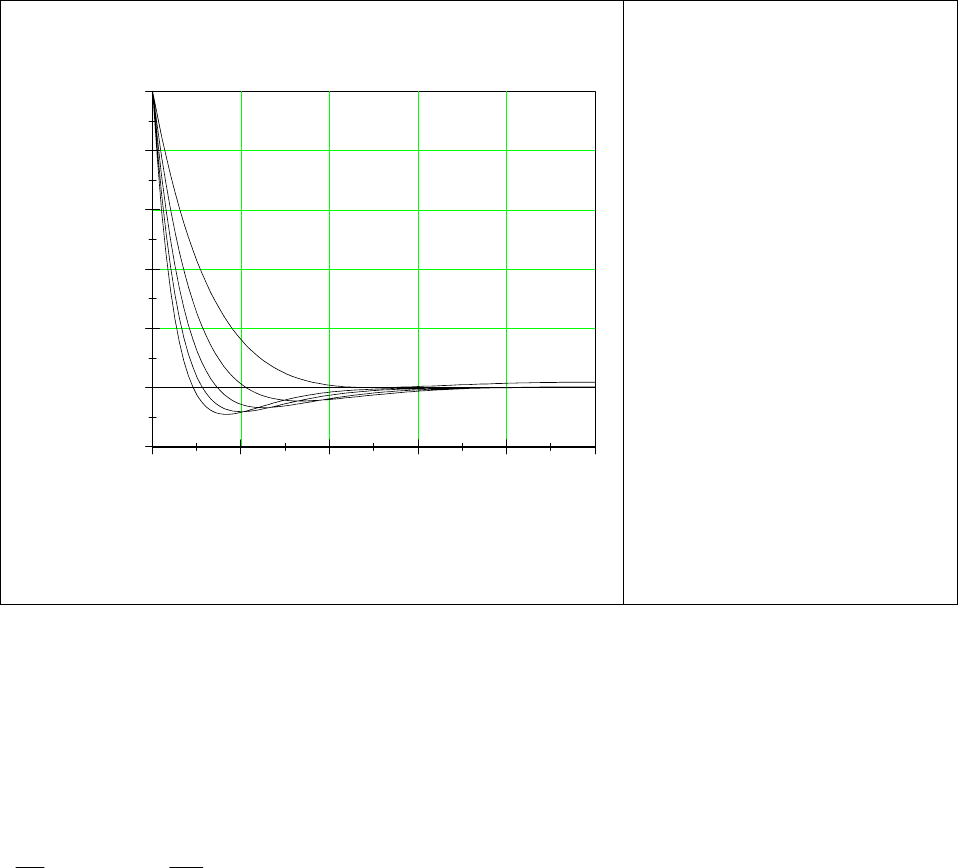
), изображенная на Рис.10 при различных
ϕ
, всегда положительна выше T
c
, а
при T<T
c
обращается в ноль на границах спинодали
θ
1s
,
θ
2s
и отрицательна внутри
спинодали. Это означает, что в спинодальной области имеет место так называемая
59
восходящая диффузия, когда диффузионный поток направлен не в сторону уменьшения, а
в сторону увеличения плотности. Такая аномальная диффузия осуществляется благодаря
притяжению частиц, которое внутри спинодали превалирует над обычным диффузионным
размытием. Уравнение (1.89) является примером уравнения типа «диффузия плюс
реакции» [103]. Однако обычно в уравнениях «диффузия плюс реакции», описывающих
формирование пространственно - упорядоченных структур
, нелинейным является
реакционный член, а диффузионный член линеен, тогда как в (1.89) нелинейным является
именно диффузионный оператор [104,105].
0.00.20.40.60.81.0
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
Coverage, θ
Diffusion coefficient, D
Рис.10. Самосогласованный
коэффициент диффузии D(θ)
при различных значениях ϕ
=4;6;8;10 и 12. С увеличением
ϕ функция D(
θ
) опускается
вниз, тем самым расширяется
спинодальная область
Рассмотрим стационарное решение уравнения (1.88) в одномерном случае, который
особенно прост для анализа. Обозначив как
η≡θ
-
θ
0
отклонение от пространственно-
однородного решения, запишем стационарное уравнение (1.88) в форме
η
η
ηθ
=
⎥
⎦
⎤
⎢
⎣
⎡
+
dx
d
D
dx
d
)(
0
(1.90)
60

Будем считать, что точка
θ
0
лежит внутри спинодали. Уравнение (1.90) с D(
θ
) в виде
(1.89) имеет первый интеграл
)()(
2
0
η
η
ηθ
U
dx
d
DK +
⎥
⎦
⎤
⎢
⎣
⎡
+=
(1.91)
где
[]
∫
−−+++−=+
′′
−=
η
ϕηηϕηηϕθηθηηη
0
23
00
)exp()()exp(2)(2)( cccaDdU
(1.92)
Константы a и c выражаются через пространственно-однородное заполнение
θ
0
:
a
≡
[3+
ϕ
(2
θ
0
-1)]/
ϕ
, b
≡
[6-
ϕ
+4
ϕθ
0
+
ϕ
2
θ
0
(
θ
0
-1)]/
ϕ
3
. Функция U(
η
), изображенная на Рис.11,
является аналогом потенциального поля в системе с полной энергией K, временем x и
зависящей от координаты
η
«массой» 2D
2
(
θ
0
+
η
). Потенциал U(
η
) имеет максимум на
границах спинодали
(нули «массы») и минимум при
η
=0, соответствующий основному
пространственно-однородному состоянию системы. Полную энергию K можно
интерпретировать как интенсивность тепловых флуктуаций. Очевидно, в системе с
полной энергией, меньшей обоих максимумов потенциала U(
η
), возникает периодическое
стационарное распределение плотности адатомов по поверхности подложки. Уравнение
K=U(
η
) имеет два решения
η
-
(K) и
η
+
(K), соответствующие минимальной и максимальной
плотности адатомов. Профиль плотности
η
(x) можно найти из (1.91) в виде обратной
зависимости
∫
+
′
−
′
+
′
±=
η
η
η
ηθ
ηη
)(
)(
)(
0
UK
D
dx
(1.93)
Амплитуда осцилляций плотности B=
η
+
-
η
-
, период осцилляций l=2x(
η
-
). Обе эти
величины возрастают с ростом
ϕ
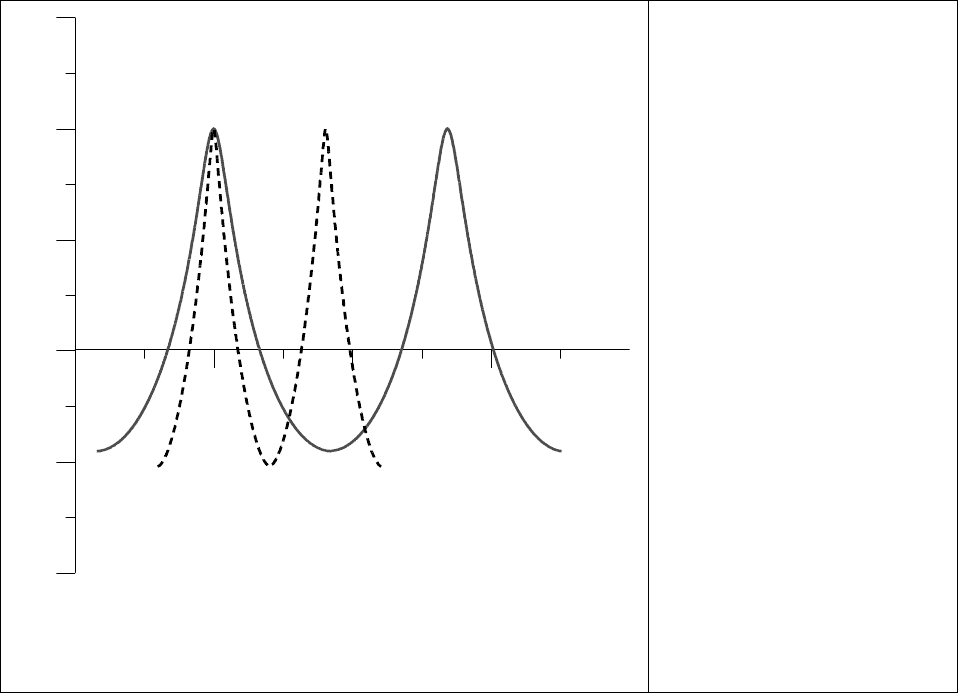
. Зависимости
η
(x), полученные в результате численного
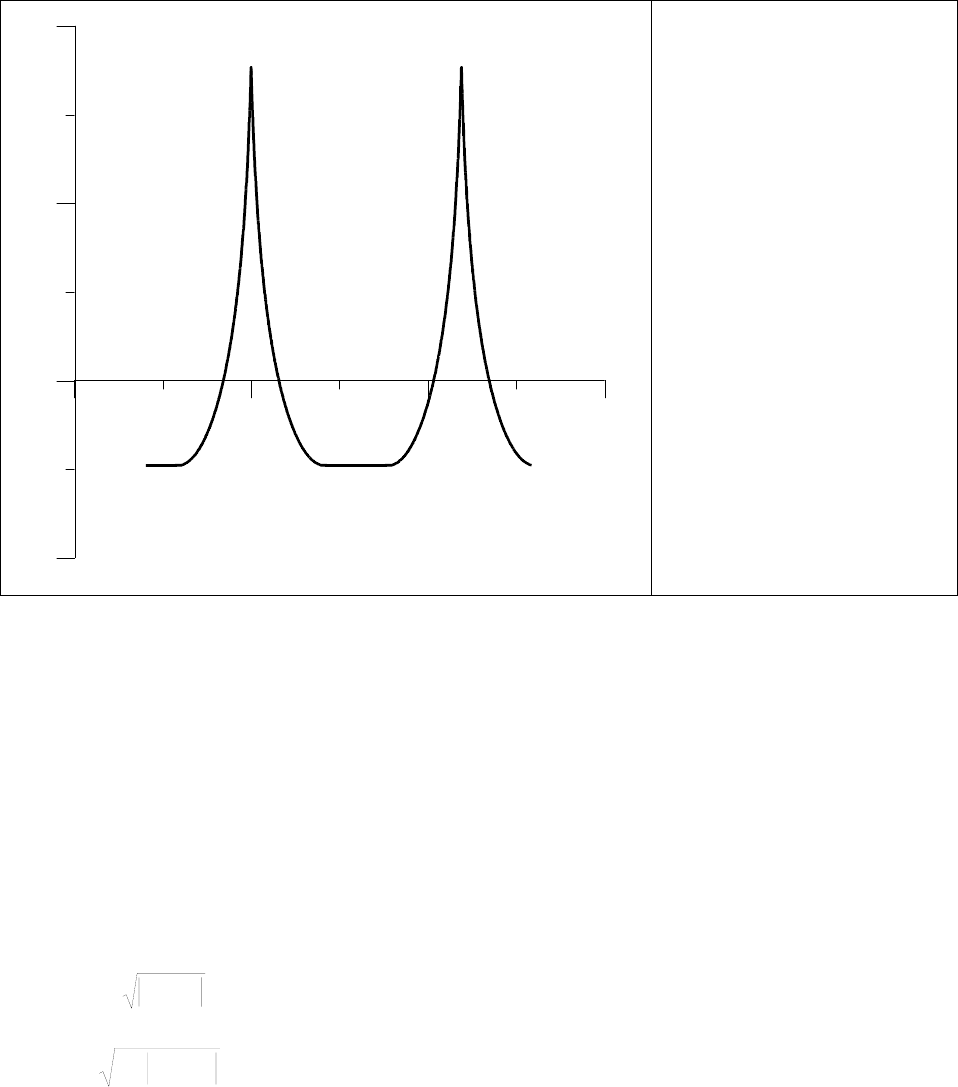
интегрирования (1.93), представлены на Рис.12. Пилообразные структуры,
соответствующие равенству К меньшему из максимумов U(
η
), изображены на Рис.13. В
61
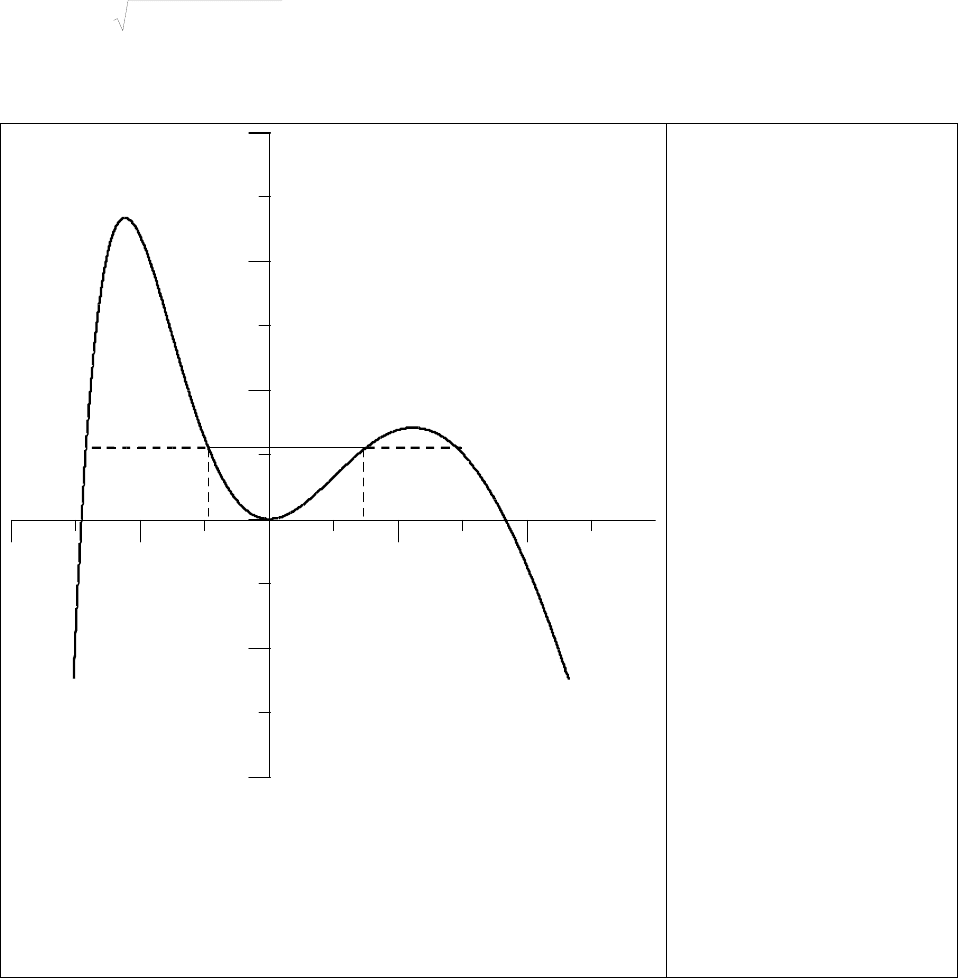
этом случае производная плотности в точке максимума испытывает конечный скачок,
равный )(/2
0 ++
+
′
ηθη
D . Возможность существования таких распределений связана с
тем, что в точке
η
+
коэффициент диффузии обращается в ноль. Поэтому производная
-0.30 -0.10 0.10 0.30 0.50
η
-0.06
-0.02
0.02
0.06
0.10
U(
η
)
η
+
η
-
K
Рис.11. Вид потенциала
U(
η
) при
θ
0
=0.5 и
ϕ
=5.
Для значения K=0.022
максимальные
отклонения заполнения
от среднего значения
θ
0
равны 0.15 и –0.1.
d
η
/dx в этой точке может быть и отличной от нуля, а условие (1.91) все равно будет
выполнено.
Численное решение дискретных уравнений (1.87) представлено на Рис.14. Оно
было получено следующим образом [10]. На неустойчивое пространственно-однородное
состояние
θ
0
=0.5 в спинодальной области накладывалось малое двоякопериодическое
возмущение при t=0 и рассчитывалась его дальнейшая эволюция. Вычисления
62
проводились на квадратной решетке 1200x1200 узлов с периодическими граничными
условиями на границе. Период начального возмущения соответствовал критическому
периоду, при котором континуальное уравнение (1.88) теряет у тойчивость по линейному с
2.50 7.50 12.50
x
-0.20
-0.10
0.00
0.10
0.20
0.30
η(x)
фиксированном
θ
0
=
к
ли
ответственно
0.104 и 0.028.
Рис.12. Профили
распределения
η
(x) при
значении
η
+
=0.2 и 0.5 для
различных значений
онстанты взаимодействия:
ϕ
=5 (пунктирная ния) и
ϕ
=8 (сплошная линия).
Соответствующие значения
K равны со
63
с у
K=U(
η
+
) при
θ
0
=0.5 и
ϕ
=8.
0.00 .0 20.00
η
(
x
)
0.00
0.40
Рис.13. Пилообразные
тр туры в случае к
10 0
0.20
x
-0.20
приближению. Подставляя в линеаризованное уравнение (1.88)
η
η
θ
η
−
∆
=∂∂ )(/ Dt
0
решение в виде диффузионной волны
)exp( trki
ωη
+=
r
r
, получаем дисперсионное
2
уравнение
0
)(1 kD
θω
−−=
, откуда видно, что неустойчивость возникает только в
спинодальной области (D(
θ
0
)<0) при возмущениях с волновым вектором
)(/1
oc
Dkk
θ
=>
. Значение k
c
соответствует критическому периоду возмущения
)(2
0
θσπ
DL
c
Γ=
(1.94)
Коротковолновые флуктуации с L<L
c
нарастают, а длинноволновые с L>L
c
–
убывают. При этом размер структур в стационарном состоянии примерно равен L
c
. Как
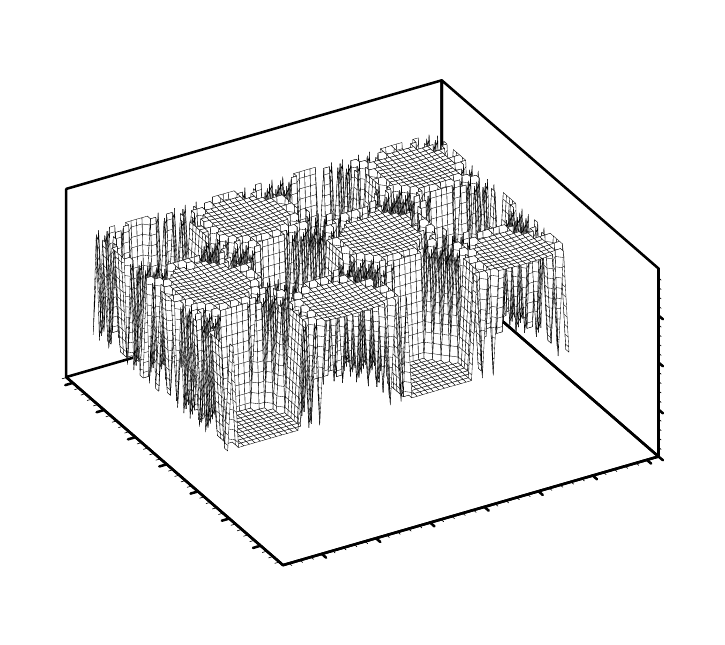
видно из Рис.14, при достаточно низких температурах поверхности (
ϕ
>5) малое линейное
периодическое возмущение с течением времени нарастает, становится нелинейным и
трансформируется в систему островков плотной фазы, имеющих четко выраженную
границу с разреженной фазой. Эти фазы находятся в динамическом равновесии друг с
64
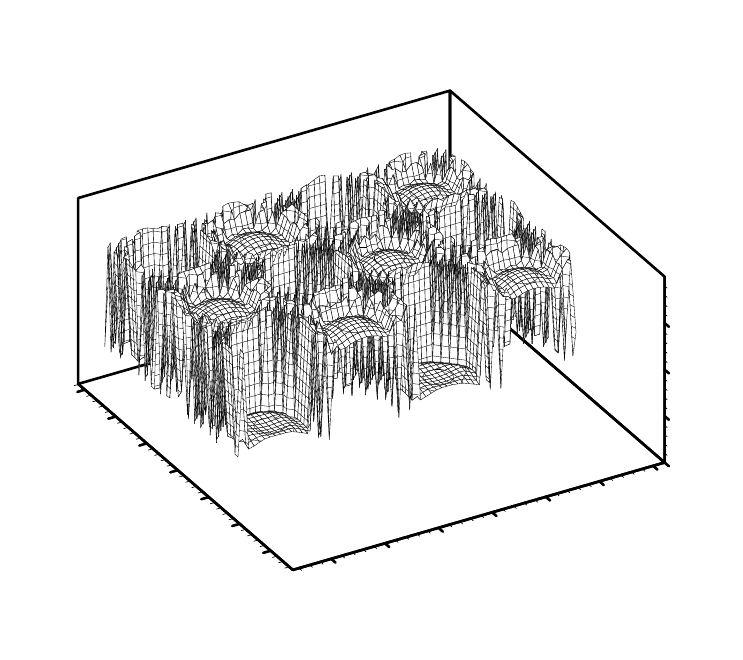
другом, по крайней мере в течение времени, много большем, чем
формирования. Такая картина эволюции системы из пространственно
неустойчивого состояния через нарастание флуктуаций к упорядоченным
структурам характерна для спинодального распада.
характерное время их
- однородного
островковым
0
0.25
0.5
0.75
Teta
0
10
20
30
40
50
60
X
0
10
20
30
40
50
60
Y
65
0
0.25
Te a
0.5
0.75
t
0
20
30
50
60
10
40
X
0
10
20
30
40
50
60
Y
Рис.14. Эволюция морфологии поверхности при спинодальном распаде, L
c
=10 нм,
θ
0
=1.2,
ϕ
=8. Вверху - момент времени t=0.01
τ
A
, внизу – стационарное состояние.
ЛЕКЦИЯ № 5. Одномерные и нульмерные квантовые наноструктуры (обзор)
I.11 Рассогласованные гетероэпитаксиальные системы. Квантовые точки.
В рассогласованных гетероэпитаксиальных системах важнейшую роль играет
процесс релаксации упругих напряжений, вызванных несоответствием решеток
осаждаемого материала и подложки. Этот процесс имеет разный характер при различных
параметрах рассогласования. Если рост идет по механизму Странского-
Крастанова,
вначале на поверхности образуется упруго-напряженный смачивающий слой, имеющий
тот же параметр решетки, материал подложки. Такой слой называют когерентным. что и
При достижении некоторой критической толщины смачивающего слоя, который мы в
дальнейшем будем называть второй критической толщиной, начинают образовываться
дислокации несоответствия. После образования таких дислокаций эпитаксиальный слой
растет с постоянной
решетки осаждаемого материала. Модель формирования дислокаций
несоответствия, позволяющая оценить вторую критическую толщину, была предложена
66

Меттьюзом и Блейксли
Рассмотрим модель р
[106]. В дальнейшем ее изложении мы следуем работе [107].
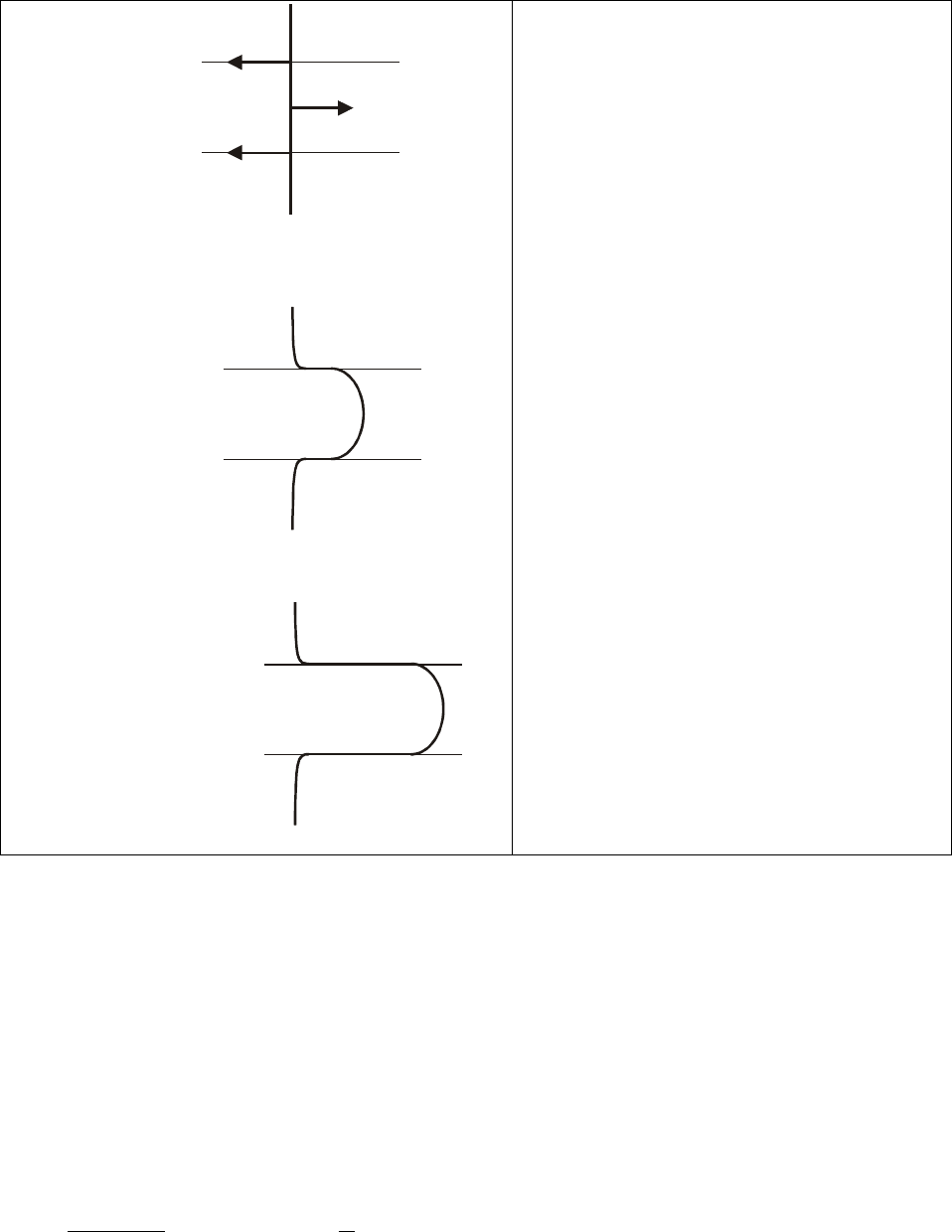
ассогласованной гетероэпитаксиальной системы, изображенную на
ис.15 для случая двойной гетероструктуры GaAs/InGaAs/GaAs. В такой модели винтовая
в правлении гетерограницы и образует
дислокацию несоответствия под действием двух сил: силы F
ε
, стремящейся удлинить
винтовую дислокацию в результате воздействия , и поверхностной силы F
l
,
действующей на ось дислокации, которая им
противоборствует развитию дислокации. До тех
и
стабильна и удлинения не происходит, пр
когерентным. При F
ε
=2F
l
обе силы уравновешивают винтовая
дислокация удлиняется и происходит релакса
дислокаций несоответствия. Силу F
ε
можно опред
Р
дислокация в когерентном слое удлиняется на
напряжений
еет противоположное направление и
пор пока F
ε
<2F
l
, винтовая д слокация
и этом напряженный слой остается
друг друга. При F
ε
>2F
l
ция напряжений через формирование
елить как
φε
ν
ν
ε
cos
)1(
)1(2
0
bh
G
F
−
+
=
(1.95)
67
GaAs
InGaAs
F
l
a)
F
F
e
l
GaAs
b)
Рис.15. Модель образования дислокации
Стадия 1 – стабильная винтовая
дислокация в когерентном слое (а),
c)
несоответствия Меттьюза - Блейксли.
стадия 2 – критическая точка,
соответствующая второй критической
толщине (b), стадия 3 – уд
винтовой дислокации и формирование
линение
дислокации несоответствия (с)
Здесь
ε
есть рассогласование , G - модуль сдвига,
ν
- коэффициент Пуассона, b –
0
решеток
вектор Бюргерса дислокации, h – толщина напряженного слоя и
φ
- угол между
направлением сдвига и направлением в плоскости поверхности пленки, которое
перпендикулярно линии пересечения плоскости сдвига и гетерограницы. Сила F
l
определяется выражением
()
⎟
⎠
⎜
⎝
+−
−
= 1lncos1
)1(4
2
b
F
l
αν
νπ
(1.96)
⎞
⎛
2
hGb
где
α
- угол между осью винтовой дислокации и вектором Бюргерса.
Сила F
l
логарифмически возрастает с ростом толщины слоя, а сила F
ε
возрастает
линейно с увеличением толщины слоя и рассогласования решеток. Для двойной
68
