Дрючин В.Г., Ткачев Р.Ю. Теоретические основы электротехники. Электрические цепи

Подождите немного. Документ загружается.

411

погрешности. Классы точности измерительных приборов, допустимые погрешности

которых выражаются по двучленной формуле, имеют более сложное обозначение.

Класс точности электроизмерительных приборов устанавливают на заводе

при калибровке по образцовому прибору в нормальных условиях. При этом

показание образцового прибора принимают за действительное значение изме-

ряемой величины. Пусть в результате калибровки вольтметра

магнитоэлектрической системы со шкалой О—50 В Получены следующие значения

абсолютной погрешности. На отметках шкалы прибора О 10 20 30 40 50 В

абсолютные погрешности составляют соответственно 0,2 0,3 0,5 0,9 В.

В этом случае приведенная погрешность поверяемого вольтметра

= ΔА

/А

ном

-100 = 0,9/50 · 100 = 1,8%,

где ΔА

= 0,9 — максимальная абсолютная погрешность прибора,

полученная на отметке шкалы 50.

Класс точности 1 ,8 для электроизмерительного прибора не установлен.

Поэтому по ГОСТу определяют ближайшее большее его значение, равное 2,5, и

поверяемый вольтметр относят к этому классу точности. '

Необходимо отметить, что класс точности прибора, характеризуя приведенную

погрешность, не является непосредственным показателем точности измерений,

проводимых с помощью этого прибора. Для этого рассмотрим следующий пример.

Пример 1.1. Необходимо измерить ток I = 4 мА. Для этого имеются два

миллиамперметра: один — класса точности 1,0 с пределом измерения 20 мА и второй

— класса точности 2,5 с пределом измерения 5 мА. Определить, у какого прибора

меньше предел допускаемой основной относительной погрешности и какой прибор

обеспечит более высокую точность заданного измерения.

Решение 1. Пользуясь формулой (2.3), определим предельные значения

абсолютной основной погрешности приборов:

ΔА

= ± γ

%А

ном

= γ

ном

/100.

При измерении прибором

класса 1,0

ΔА

= ± 1,0-20/100 = ± 0,2 мА;

класса 2,5

ΔА

= ±2,5-5/100= ±0,125 мА.

412

2. Определим наибольшие относительные погрешности измерения

приборов

= ΔА

/А 100 = ± 0,2·100/4= ± 5 %;

= ΔА

/А 100 = ±0,125/4. 100 = ±3%.

Как видно, для заданного измерения лучше использовать второй прибор

класса точности 2,5 с пределом 5 мА, обеспечивающий значительно меньшую

относительную погрешность измерения.

Классификация радиоизмерительных приборов имеет следующие

особенности.

1. Низкочастотные генераторы сигналов согласно ГОСТ 10501 —74 делятся на

классы точности по частотным параметр JM (F-параметрам) и параметрам выходного

напряжения (U-параметрам). За индекс класса принимается значение основной

погрешности установки частоты и опорного уровня выходного напряжения в

процентах. Так, обозначение класса точности F

показывает, что генератор имеет

основные погрешности по частоте 2% и установки опорного уровня выходного

напряжения 4%. Этот ГОСТ устанавливает шесть классов точности отсчета

частоты: F

0.1

, F

0.5

, F

1й

, F

и F

и пять классов точности отсчета уровня

выходного напряжения U

, U

2й

, U

и U

2. Генераторы радиовещательного диапазона делятся на классы точности

согласно ГОСТ 10622—70. Принцип их классификации примерно такой же, как у

низкочастотных генераторов.

Важной характеристикой измерительного прибора является вариация его

показаний, определяемая как разность между двумя его показаниями,

соответствующими одному и тому же действительному значению измеряемой

величины, устанавливаемому после плавного ее изменения один раз в сторону

возрастания, а второй — в сторону убывания. Этот параметр нормируется пределом

допускаемого значения или указывается в процентах; так, например, в электронном

вольтметре В7-26 вариация показаний прибора не превышает 1,0 %, а основная

погрешность при измерении постоянного напряжения составляет в зависимости от

предела измерения ± (2,5 ÷ 4,0)%.

Вариация показаний проявляется от наличия трения в опорах, люфта

кернов в подпятниках, механического гистерезиса пружинок, магнитного гистерезиса

деталей измерительного механизма, и поэтому погрешности такого вида наиболее

413

характерны для электромеханических приборов. В соответствии с ГОСТом в

обоснованных случаях допускается не нормировать вариацию показаний.

Расчет погрешностей измерений

Определение абсолютных и относительных погрешностей измерений,

поправки, а также приведенной погрешности прибора выполняется в соответствии

с формулами (2.1)—(2.3). Способ расчета методических погрешностей, возникающих

из-за влияния на режим цепи, включение прибора поясняется на примерах типовых

измерительных схем. Дополнительные погрешности, как правило, рассчитываются в

соответствии с указаниями и формулами, которые даны в инструкции к прибору.

Поэтому расчет погрешностей этого вида выполнен применительно к конкретному

типу прибора.

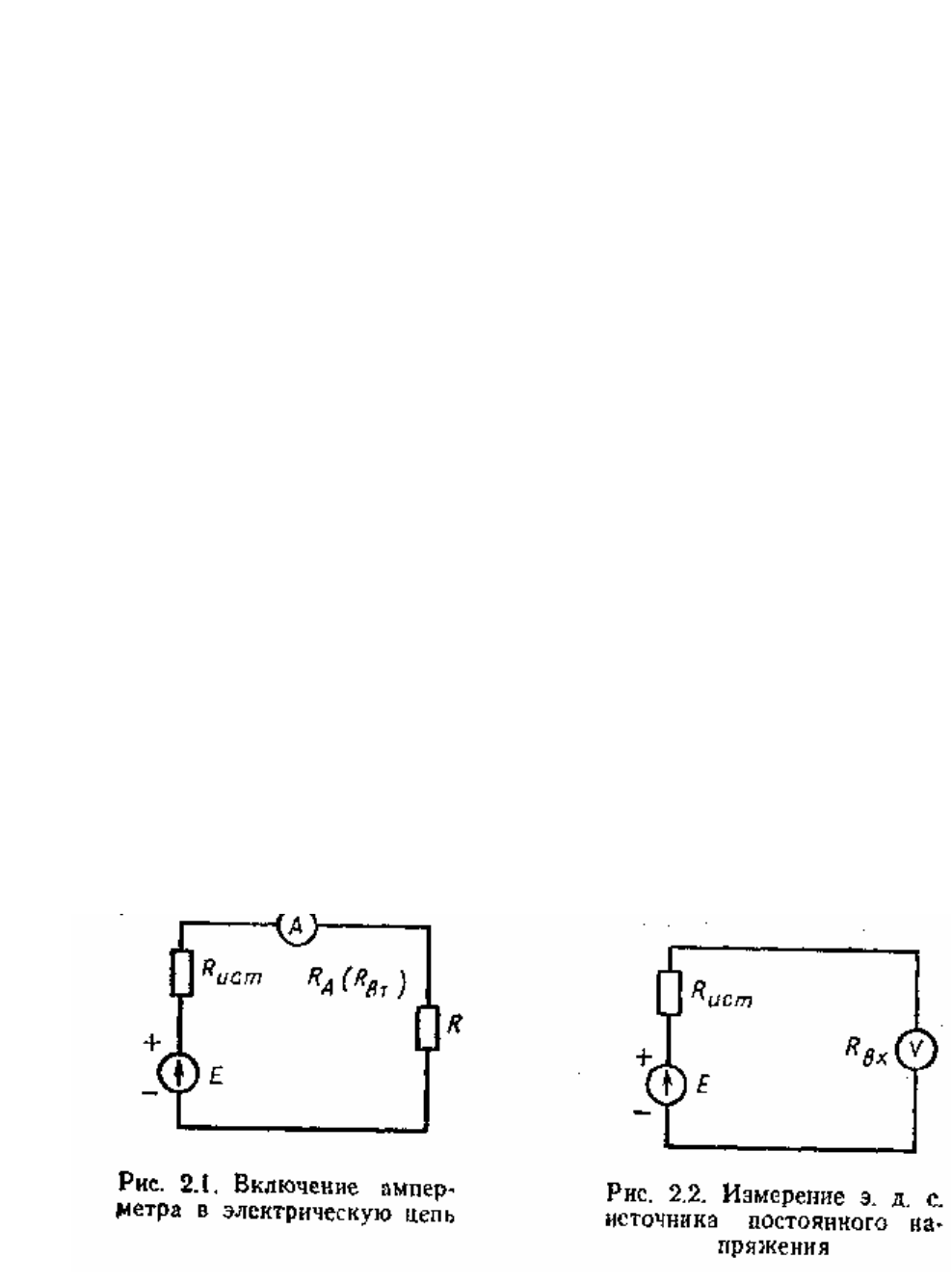
Измерение тока. В электрическую цепь включается измеритель тока (рис. 2.1).

Результат измерения содержит методическую погрешность δ'*

δ = - (R

/( R

ИСТ

+ R + R

))·100 = - (R

·100)/(R

ВХ

+ R

) =

= - (1/(1-( R

ВХ

+ R

))) ·100 … (2.4)

* Здесь и далее относительную погрешность измерения, обусловленную

внутренним (входным) сопротивлением прибора (амперметра или вольтметра),

обозначают о' в отличие от относительной погрешности, определяемой классом

точности прибора и обозначаемой 6 (без штриха).

414

где R

нст

— сопротивление источника Е; R

— внутреннее сопротивление

прибора R

вт

; R- сопротивление (нагрузка); R

вх

= R + R

ист

— входное

сопротивление цепи со стороны измерителя тока. Если R

ист

« R,

то δ’ ≈ -(1/(1+R /R

))

(2,5)

вх

- указывается в справочнике.

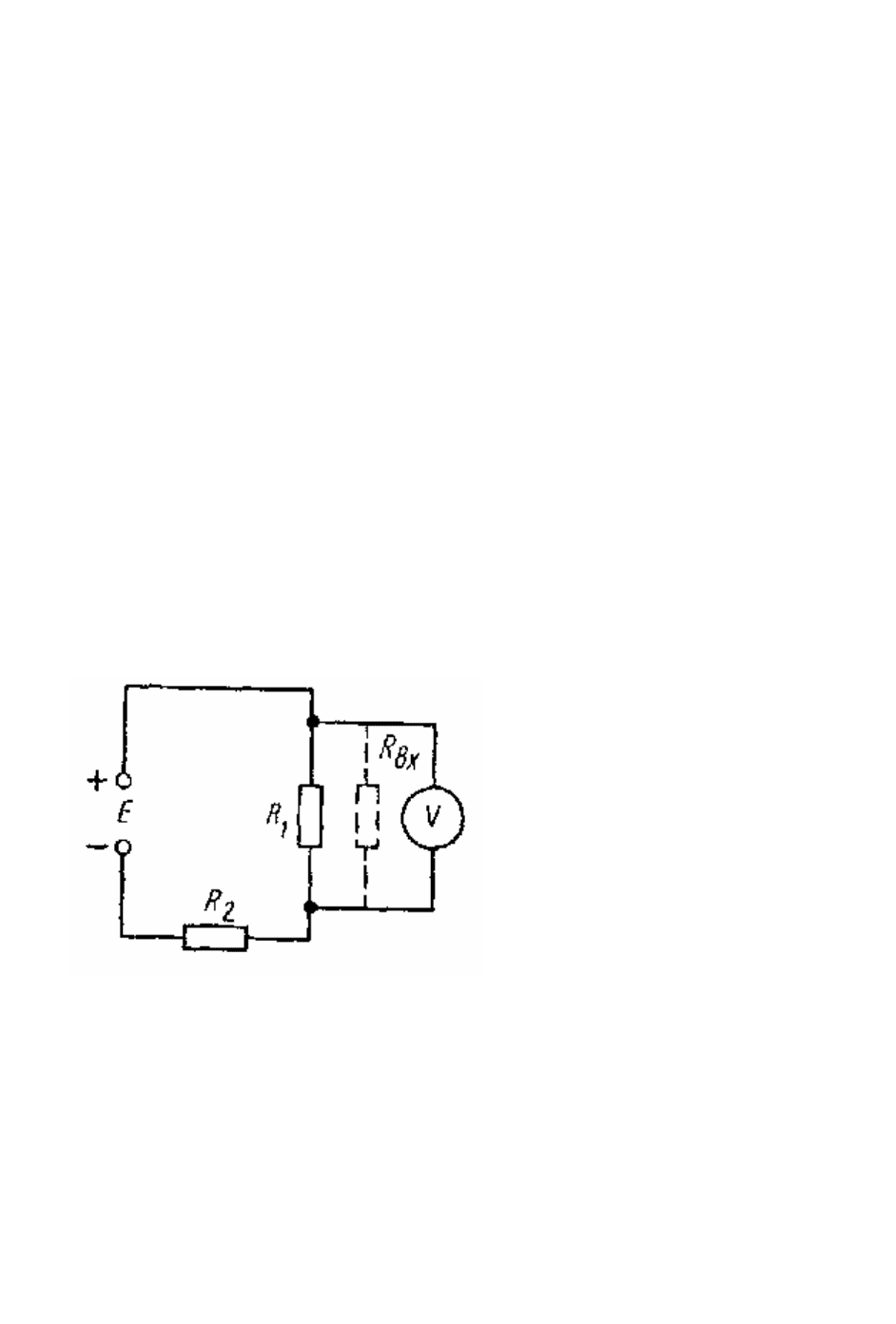
Измерение вольтметром э.д.с. источника постоянного напряжения.

Действительное значение измеряемой величины э.д.с.

= U

(1 + R

ист

вх

) (2.6)

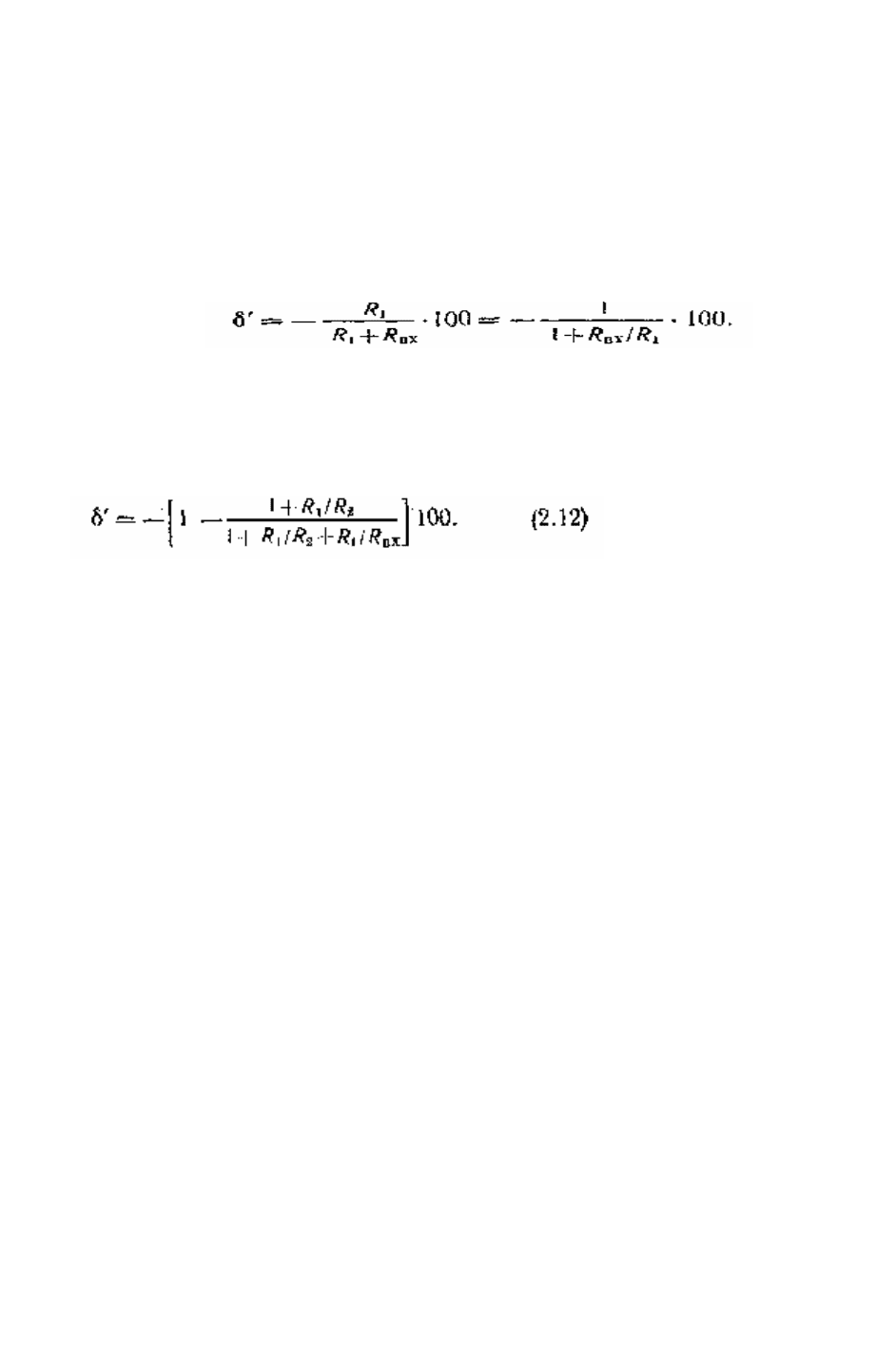
Измерение вольтметром напряжения на отдельном участке

электрической цепи. Действительное значение измеряемой величины напряже-

ния (рис. 2.3)

Рис. 2.3. Измерение напряжения на

участке электриче

ской цепи.

= U

((1+ R

/ R

+ R

вx

)/(1+ R

)) (2.8)

где U

— значение напряжения, отсчитываемое по вольтметру

Если R

вх

»R

Т0 U

≈ U

. т. е. вольтметр не вносит погрешность

Если R

вx

соизмеримое R

, но R

» R

, то

= U

(\ + R

вx

(2.9)

Формулы (2.8) и (2.9) позволяют определить: 1) поправку, которую нужно

внести в результат измерения на шунтирующее действие прибора; 2) значение

где U

— показания прибора; R

— входное сопротивление

вольтметра.

Относительная погрешность измерения

415

требуемой величины R

прибора, чтобы погрешность измерения не превышала

заданного значения.

Относительная погрешность измерения, обусловленная входным

сопротивлением прибора:

δ' = ΔU/U

•100 = (U

— U

)/U

•100. (2.10)

Для случая R

»R

, подставляя в (2.10) значение из (2.9) и произведя

преобразования, получим

(2,11)

Если R

соизмеримо с R

, то подставляя значение из уравнения (2.8) в

уравнение (2.10) и произведя преобразования, найдем

При пользовании формулами (2.8), (2.9), (2.11) и (2.12), следует помнить, что R

означает сопротивление резистора, на котором измеряется напряжение, a R

—

сопротивление всех резисторов, последовательно соединенных с R

и образующих

вместе с ним и с источником питания замкнутую электрическую цепь.

Для случая R

»R

можно из (2.11) определить значение R

вх

вольтметра, при

котором обеспечивается заданная относительная погрешность δ'

зал

вх

= R

(1/δ'

зад

– 1). (2.13)

Задача 2.1. При проверке после ремонта вольтметра класса 1,5 с конечным

значением шкалы 5 В в точках шкалы 1, 2, 3, 4, 5 В получены соответственно следующие

показания образцового прибора: 0,95; 2,07; 3,045; 4,075; 4,95 В. Определить,

сохранился ли класс точности прибора.

Ответ: да сохранился, так как класс точности прибора.

=(ΔА)

n max

100/А

ном

=-0 ,075/5•100 = - 1 ,5%.

Задача 2.2. В электрическую цепь (см. рис. 2.1), состоящую из источника

Е=10В, R

ист

=2Ом и R =100 Ом, включен миллиамперметр М260М класса

точности К

= 2,5, R

вт

= 2 Ом с конечным значением шкалы 100 мА. Показание

прибора 94 мА. Определить погрешность результата измерения, обусловленную: а)

416

классом точности и пределом измерения прибора; б) внутренним сопротивлением

прибора (R

вт

Решение. 1. Относительная погрешность, обусловленная классом

точности и пределом измерения прибора: δ

= ±К

ном

/I•100=±2,5100/94• 100 =

± 2,66%.

2. Относительная методическая погрешность при R

пет

3. Общая максимальная погрешность измерения: так как б'иδ

соизмеримы, то б

общ

= δ' + δ

= - (1,96 + 2,66) = — 4,62 %, округляя, получим

о0щ

= - 4,6%, что соответствует - 4,3 мА.

Примечание. Действительное значение измеряемой величины тока с учетом

знака погрешности равно 94 + 4,3 = 98,3 мА.

2. Погрешность метода можно не учитывать, если δ' ≤0,2δ

Задача 2.3. Из имеющихся двух миллиамперметров с конечным значением

шкалы 5 мА: 1) типа М260М класса точности K

, = 2,5, R

вт

= 50 Ом и 2) типа

М4225 класса точности K

, = 2,5, R

вт

= 25 Ом, необходимо выбрать один.

Выбранный прибор должен обеспечить наименьшую общую погрешность измерения

тока 4,6 мА в схеме рис. 2.1, состоящей из источника E =2 В,

пст

=5 Ом, R = 400 Ом.

Решение: Прибор М260М.

1 . Относительная методическая погрешность при R

ист

«R

2. Относительная погрешность измерения прибора δ

= ± ΔI/I = ±K

ном

/I•

• 100 = ±2,5-5/4,6•100 =±2,7%.

Очевидно, что такое же значение 6

имеет прибор М4225.

3. Общая погрешность измерения

общ

= δ' + δ

= - (11.1 + 2.7) = - 13,8 %.

Прибор M4225.

1. Относительная методическая погрешность при R

ист

«R

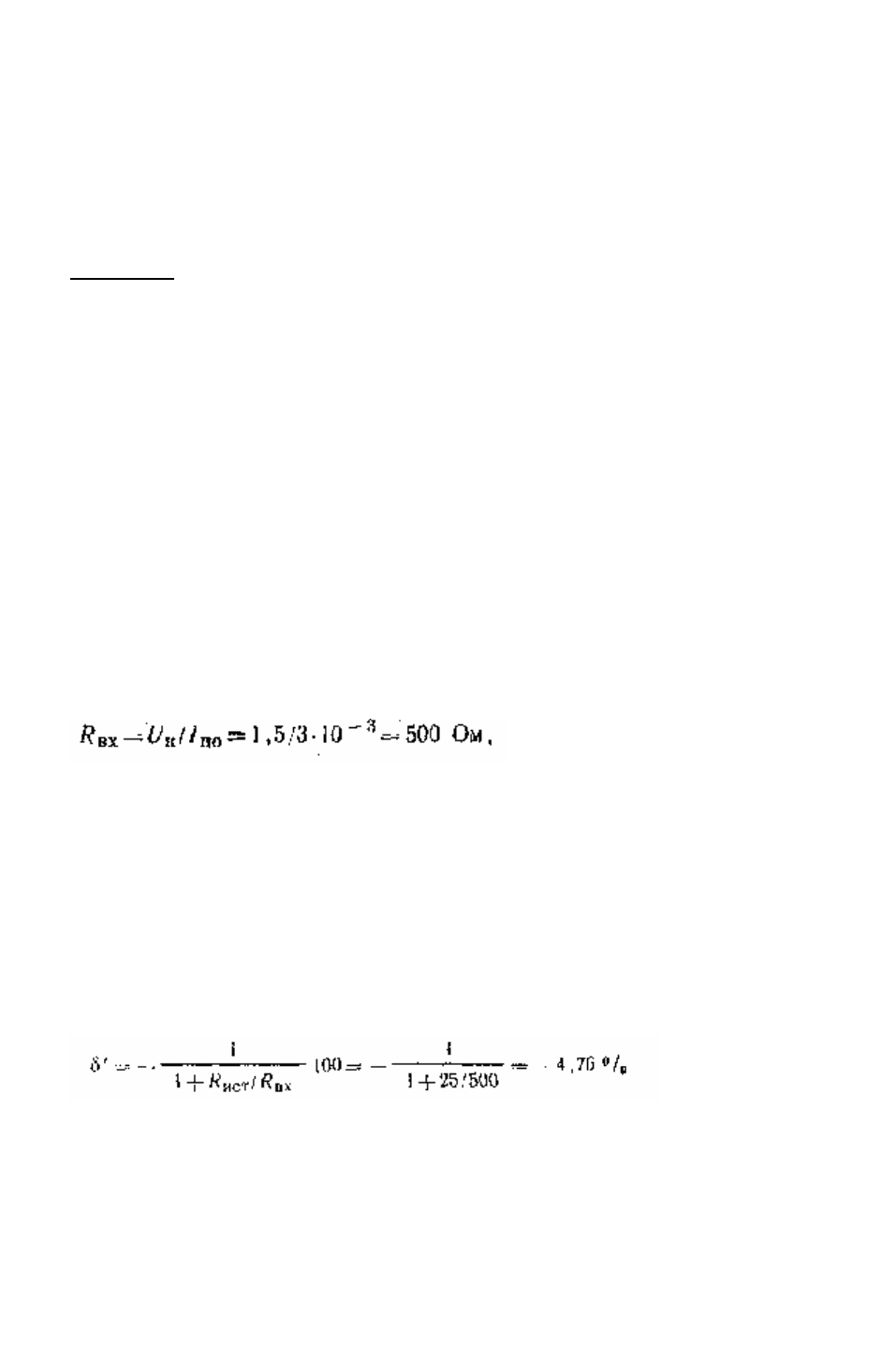
417

2. Общая погрешность измерения

общ

= δ' + δ

= - (5,9 + 2.7) = - 8,6 %

Окончательно выбираем прибор М4225.

Задача 2.4. Каковы должны быть отношения внутренних сопротивлений

измерителей тока R

вт

к' сопротивлениям нагрузки R, чтобы погрешности метода

измерения δ' не превышали: а) 10, б) 1, в) 0,1%.

Указание. При расчете принять, что R/R

вт

»· 1 и воспользоваться

упрощенной формулой (2.5).

Ответ: а) 0,1; б) 0,01; в) 0,001.

Задача 2.5. Э. д. с. источника постоянного тока с сопротивлением R

ист

= 25

Ом измеряется вольтметром класса точности К

- 0,5. Шкала прибора имеет 150

равномерных делений. Ток полного отклонения указателя 3 мА. Результат

измерения по шкале с конечным значением 1,5 В составляет 97,5 делений, что со-

ответствует 0,975 В. Отсчет выполнен с точностью до половины деления шкалы или

0,005 В. Определить действительное значение измеряемой величины э. д. с. и

методическую погрешность измерения из-за влияния вольтметра на измеряемую

цепь.

Решение. 1. Входное сопротивление вольтметра на шкале 1.5 В.

где U

— конечное значение используемой для измерения шкалы; / „„ —

ток полного отклонения шкалы.

2. Действительное значение измеряемой э. д. с согласно (2.6)

= U

(1 + R

ист

вх

) = 0,975 (1 + 25/500) = 1,024 В

3. Относительная методическая погрешность измерения со

гласно (2.7)

4. Относительная погрешность измерения, обусловленная классом точности и

пределом измерения прибора:

= ± K

•100= ± 0,5-1.5/0,975•100= ± 0,77%

что примерно в 6 раз меньше методической погрешности, и. следовательно,

можно ею пренебречь по сравнению с методической при расчете общей погрешности

измерения.

418

Задача 2.6. Для определения наиболее достоверного значения измеряемого

напряжения и уменьшения влияния случайных погрешностей выполнен в

одинаковых условиях и одним и тем же прибором ряд повторных измерений

напряжения в количестве n = 10 (табл. 2.1). Определить: а) действительное значение

величины измеряемого напряжения; б) имеются ли в результатах измерений грубые

ошибки (промахи).

Решение. 1. Среднее значение измеряемого напряжения; наиболее достоверное,

принимаемое за действительное:

где U

— показание единичного измерения, указанное в табл. 2.1.

Абсолютная погрешность единичного измерения

Δ U

- U

ср

;

Δ U

- U

ср

=149,52 — — 151,04 = —1,52 В;

где i — номер единичного измерения.

Значения абсолютных погрешностей всех единичных

измерений определены аналогичным образом и приведены

в табл. 2.1.

2. Проверяем правильность вычислений; для этого определяем сумму

абсолютных погрешностей всех единичных измерений, которая должна быть равна

нулю: —(1,52 + + 0,56 + 0,79 + 0,40 + 1,17 + 0,29) + (1,09 + 0,32 +

+ 2,28+ 1,04) = О.

Проверка показывает, что вычисления выполнены правильно.

3. Среднеквадратическое отклонение погрешности σ, характеризующее учайную

погрешность единичного измерения:

419

Принимаем, что отклонение значения единичного измерения υ

ι от среднего U

(максимальная или предельная погрешность единичного измерения) не должно

превышать 3σ*. Поэтому результаты измерений, отклоняющиеся от U

больше

чем на 3σ, не учитываем. В данном случае 3σ = 3•1,666 = 3,5 и, как следует из

табл. 2.1, ни одно из ряда измерений не отклоняется на такое значение от

сp

= 151,04 В. Следовательно, грубых ошибок (промахов) в выполненном

ряде измерений нет.

4. Среднеквадратическое отклонение среднего арифметического

(среднеквадратическая погрешность результата измерений)

ρез

= σ/√n = 1,16/√10= 0,366 В.

Ранее было принято, что доверительный интервал (предельная или

максимальная погрешность) равен Зσ, В этом случае для той же доверительной

вероятности (р = 0,9973) границы доверительного интервала выполненных измерений

относительно среднего арифметического значения равны U± Зσ/√n= =U± Зσ

рез

Следовательно, в этом случае результат измерений можно записать так: U

=151,04±3·0,366 = 151,04 ± 1,098 В или, округляя, получим U = 151 ± 1 В.

Если известен закон распределения случайных погрешностей, то можно

определить вероятность появления погрешностей δ, находящейся в заданном

интервале от δ

до δ

. Этот интервал называют доверительным интервалом, а

характеризующую его вероятность — доверительной вероятностью. При увеличении

доверительных интервалов значения доверительных вероятностей возрастают,

стремясь к пределу, равному единице. Например, для доверительного интервала от δ

= — σ до δ

= +σ доверительная вероятность ρ равна 0,683*. Следовательно,

вероятность того, что случайная погрешность не превышает среднеквадратического

значения σ, равна 0,683 и вероятность появления погрешности по абсолютному

значению, превышающей σ, равна 1 - 0,683 = 0,317, т.е. примерно одно из трех

измерений будет иметь погрешность, большую σ. Для доверительного интервала от δ

420

= — 2σ до δ

= +2σ, ρ = 0,954 и вероятность появления погрешности по

абсолютному значению, превышающей 2σ, равна 1 - 0,954 = 0,046 ≈ 1/217. Это

означает, что из 217 случайных погрешностей только одна погрешность

по абсолютному значению будет больше 2σ. Для доверительного интервала от

—3σ до +3σ доверительная вероятность ρ равна 0,9973. Вероятность появления

случайной погрешности, большей 3σ, равна 1 - 0,9973 = 0,0027 ≈ 1/370. Это

означает, что из 370 случайных погрешностей только одна погрешность по

абсолютному значению будет больше 3σ. Поэтому значение 3σ считается

максимально возможной случайной погрешностью. Погрешности больше

За считаются промахом и при обработке результатов измерений не

учитываются. Чем больше доверительный интервал, тем вероятнее, что

результаты измерения не выйдут за его пределы. Очевидно, что при этом будет

больше допустимая погрешность (точность измерения уменьшается).

При большинстве обычных измерений можно ограничиться значением

доверительной вероятности 0,954 или 0,997. На практикуме обычно принимают

нормальный закон распределения и указывают в индивидуальных заданиях зна-

чения доверительной вероятности или доверительного интервала.

Ранее указывалось, что точность результата η измерений

характеризуется оценкой σ

ρез

= σ/√n; она выше точности единичного измерения,

характеризуемого оценкой σ. С увеличением числа измерений η (при

независимых результатах) точность увеличивается пропорционально √n.

Однако в практике измерений п> 10 встречается редко. Для количества

измерений 2 < n < 20 при нормальном законе распределения для

определения доверительного интервала (максимальной погрешности результата

измерений) нужно пользоваться коэффициентами Стьюдента — t

n,р

. который

зависит от количества измерений n и задаваемой доверительной вероятности ρ

(табл. 2.2).

Для определения доверительного интервала среднеквадратическую

погрешность σ

рез

надо умножить на коэффициент t

n,р

. Например:ρ = 0,95;n = 5.

Из табл. 2.2 находим, что t

n,р 0.5

= 2,8. Тогда доверительный интервал

(максимальная погрешность) равен ± 2,8 σ

рез

, и результат измерения можно

записать так: А = A

ср

+ t

n,р

рез

, где Aср — среднее арифметическое значение

измеренной величины. Легко убедиться, что при использовании распределения

Стьюдента доверительный интервал расширяется при той же самой

доверительной вероятности. Так, например, при количестве измерений n = 10 и