Drennan R.D. Statistics for Archaeologists: A Common Sense Approach
Подождите немного. Документ загружается.

164 CHAPTER 12
3. What, exactly, have you calculated the probabilities of in Question 2? What,
exactly, are the populations you have characterized? What are the logical links
necessary to use this evidence in support of the conclusion you want to make
about obsidian sources?
4. Approach Question 2 using a t test. How strong and significant is the difference
in zirconium content between black and gray obsidian? What is your estimate
of that difference with an error range at the 95% confidence level? State the
conclusions derived from your t test in a single clear sentence as if you were
reporting it in a paper.

Chapter 13
Comparing Means of More than Two Samples
Comparison with Estimated Means and Error Ranges ........................................... 166
Comparison by Analysis of Variance .............................................................. 168
Strength of Differences............................................................................. 174
Differences between Populations versus Relationships
between Variables
............................................................................ 176
Assumptions and Robust Methods ................................................................ 178
Practice.............................................................................................. 179
In Chapter 12 we took two approaches to comparing the means of two samples. The
first approach involved using each sample separately to estimate the mean of the
population that the sample came from. We then attached error ranges for several
confidence levels to these estimates and drew a picture of the whole thing with a
bullet graph (Fig.
12.1). This approach is easily extended to the comparison of any
number of samples. In this chapter we will use another fictitious example consisting
of 127 Archaic projectile points from the Cottonwood River valley. After consid-
ering possible sources of bias we decide to work with these as a random sample
from the large and vaguely defined population of Archaic projectile points from the
Cottonwood River valley.
We are interested in whether, during the Archaic period, there was much change
in hunting of large and small animals in the Cottonwood River valley. We reason
that large projectile points are more involved in hunting large animals and small
projectile points are more involved in hunting small animals. We can divide the
127 projectile points into three groups: Early, Middle, and Late Archaic, and we
decide to compare the weights of projectile points in these three periods. One way
to organize these data for this sample is shown in Table
13.1. Here two observations
are recorded for each of the 127 projectile points: the weight (in grams) and the
period (Early, Middle, or Late Archaic). Our two variables, weight and period, are
of different kinds. Weight, of course, is a measurement, and period is a set of three
categories.
R.D. Drennan, Statistics for Archaeologists, Interdisciplinary Contributions
to Archaeology, DOI 10.1007/978-1-4419-0413-3
13,
c
Springer Science+Business Media, LLC 2004, 2009
165

166 CHAPTER 13
Table 13.1. Data on Weight and Period for a Sample of Archaic Period Projectile Points
from the Cottonwood River Valley
Weight Archaic Weight Archaic Weight Archaic Weight Archaic
(g) Subperiod (g) Subperiod (g) Subperiod (g) Subperiod
54 Early 68 Early 63 Middle 69 Middle
39 Early 68 Early 52 Middle 80 Middle
49 Early 85 Early 44 Middle 78 Middle
65 Early 49 Early 73 Middle 69 Middle
54 Early 21 Early 70 Middle 34 Late
83 Early 24 Early 56 Middle 39 Late
75 Early 50 Early 46 Middle 40 Late
45 Early 52 Early 61 Middle 45 Late
68 Early 62 Early 49 Middle 37 Late
47 Early 44 Early 51 Middle 32 Late
57 Early 61 Early 61 Middle 31 Late
19 Early 30 Early 70 Middle 60 Late
47 Early 52 Early 51 Middle 58 Late
58 Early 56 Early 42 Middle 45 Late
76 Early 63 Early 73 Middle 50 Late
50 Early 53 Early 51 Middle 40 Late
67 Early 79 Early 74 Middle 41 Late
52 Early 50 Early 40 Middle 38 Late
40 Early 54 Early 67 Middle 59 Late
58 Early 51 Early 51 Middle 37 Late
42 Early 59 Early 59 Middle 28 Late
43 Early 60 Early 68 Middle 37 Late
58 Early 48 Early 63 Middle 31 Late
28 Early 40 Early 64 Middle 40 Late
59 Early 50 Early 78 Middle 34 Late
43 Early 69 Early 62 Middle 37 Late
45 Early 71 Middle 78 Middle 44 Late
60 Early 64 Middle 57 Middle 47 Late
27 Early 59 Middle 59 Middle 54 Late
64 Early 65 Middle 31 Middle 36 Late
73 Early 54 Middle 69 Middle 48 Late
70 Early 65 Middle 32 Middle
COMPARISON WITH ESTIMATED MEANS
AND ERROR RANGES
We can use the three period categories to separate the sample of 127 projectile
points into three samples – one consisting of the 58 Early Archaic points, one of
the 42 Middle Archaic points, and one of the 27 Late Archaic points. If we were
willing to treat the 127 projectile points as a random sample from the Archaic pro-
jectile points of the Cottonwood River valley, then we can be equally willing to treat

COMPARING MEANS OF MORE THAN TWO SAMPLES 167
Table 13.2. Comparison of Weights of Projectile Points for
Archaic Subperiods
Early Middle Late All Archaic
n = 58 42 27 127
X = 53.67 g 60.45 g 41.56 g 53.34 g
s = 14.67 g 12.15 g 8.76 g 14.42 g
SE = 1.93 g 1.88 g 1.69 g 1.28 g
s
2
= 215.21 147.62 76.74 207.94
the 58 Early Archaic points as a random sample of the Early Archaic points of the
Cottonwood River valley, the 42 Middle Archaic points as a random sample of the
Middle Archaic projectile points of the Cottonwood River valley, and the 27 Late
Archaic points as a random sample of the Late Archaic points of the Cottonwood
River valley. If we do this, then we have reorganized a single batch of numbers into
three batches of numbers that can be compared just as we compared the two batches
of numbers in Chapter
12.
Table
13.2 provides numerical indexes (sample size, mean, standard deviation,
standard error, and variance) for each of these three smaller samples. Using the
standard errors and Table
9.1 we can provide estimated mean weights for each of
the three populations these samples came from and present the whole comparison
graphically as in Fig.
13.1. The Early Archaic and Middle Archaic samples are large
enough that we can count on a special batch with a normal shape. The Late Archaic
sample is a bit small for us to count on a normal shape for the special batch, so
we look at the stem-and-leaf plot for Late Archaic in Fig.
13.1 to make sure that
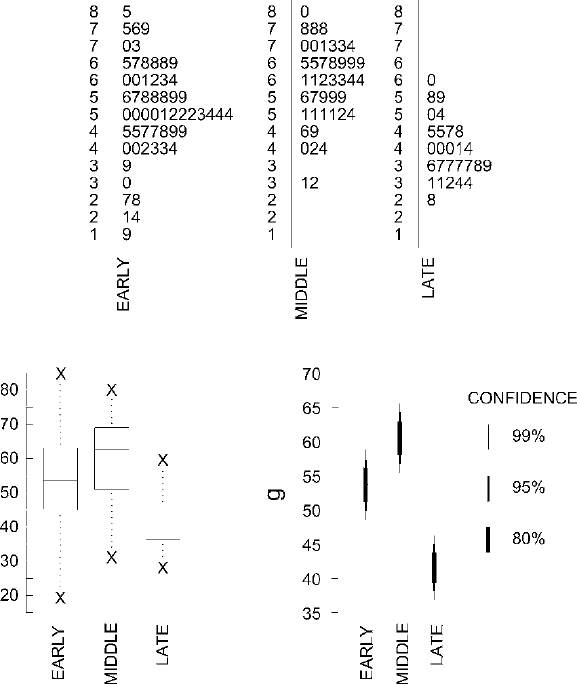
the sample itself has a fairly normal shape (which it does). The box-and-dot plot
makes clear that Middle Archaic projectile points tend to be the heaviest and Late
Archaic projectile points the lightest, with Early Archaic projectile point weights
falling in between. The ranges of all three certainly overlap, however, especially
those of Early Archaic and Middle Archaic. At the far right in Fig.
13.1, the bullet
graph of estimated population means with error bars for confidence levels of 80%,
95%, and 99% makes it clear that the differences between the three samples we have
are very highly significant. None of the error ranges for 99% confidence includes
the estimated mean of any of the other populations. We are thus more than 99% con-
fident that the differences we observe between samples are not just a consequence
of the vagaries of sampling. It is extremely likely instead that such different samples
came from parent populations that differed from each other.
Figure
13.1 demonstrates once again that box-and-dot plots and bullet graphs are
two different things. The boxes representing the midspreads for the three periods
overlap substantially, while the error ranges for 80%, 95%, and 99% confidence do
not. Since these two kinds of plots are similar in appearance and since both deal with
the spreads of batches in one way or another, it is easy to overlook the fundamental
difference between the two. While it is true that the error ranges in the bullet graph
in Fig.
13.1 are based, in part, on the spread of each batch, they are not simply a
graphical representation of that spread. They rely as well on the sample sizes and are
168 CHAPTER 13
Figure 13.1. Comparison of projectile point weights by period.
thus a picture not of the spreads of the three sample batches but rather of the spreads
of the corresponding special batches, as discussed in Chapter
8. As a consequence,
the bullet graphs have useful implications concerning the parent populations that the
box-and-dot plots do not have.
COMPARISON BY ANALYSIS OF VARIANCE
Estimating means and attaching error ranges to each estimate provides a good way
to compare each sample with each other sample, and a bullet graph literally draws
the overall picture. In terms of significance, this overall picture is summed up in the
question, “How likely is it that we could get three samples with means and standard

COMPARING MEANS OF MORE THAN TWO SAMPLES 169
deviations like these from a single parent population?” Another way to say it would
be, “What is the probability that samples as different as these three could be pro-
duced from the same population just through the vagaries of sampling?” When we
speak of a “single parent population” or the “same population” in these questions,
we are speaking metaphorically, since we know the three samples came from three
different populations, one of Early Archaic projectile points, one of Middle Archaic
projectile points, and one of Late Archaic projectile points. Hypothesizing here that
they may have come from the “same population” is simply shorthand for inquiring
how likely it is that the three populations these three samples came from had the
same mean. Thus, the significance question we are asking amounts to, “How likely
is it that Early Archaic, Middle Archaic, and Late Archaic projectile point popula-
tions all had the same mean weight, and that our three samples differ just because
random samples, even from the same population, do differ from each other?”
We answered such a question with a two-sample t test in Chapter
12, but this test
cannot easily be extended to more than two samples. For three or more samples,
the technique of choice is analysis of variance, often abbreviated ANOVA.Asthe
name implies, analysis of variance relies on variance as the key to answering the
significance question in this situation. (Remember that the variance of a batch is
simply the square of the standard deviation.) The variances (s
2
) of all three separate
subsamples and of the entire sample of 127 are given in Table
13.2.
Analysis of variance assumes that the samples are drawn from populations with
normal shapes. We examine the stem-and-leaf plots for the three separate subsam-
ples in Fig.
13.2, and we see the fundamentally single-peaked and symmetrical
shape that we need to see for each of the subsamples. Analysis of variance also
assumes that the spreads (specifically the variances) of the populations are approx-
imately equal. The box-and-dot plots in Fig.
13.1 provide an easy way to judge
the spreads of the samples, as do the figures for the variances given in Table
13.2.
Figure 13.2. Stem-and-leaf plots of projectile point weights by subperiod where all subperiod
groups have similar means.
170 CHAPTER 13
Here the largest variance is almost three times as big as the smallest. Comparing
midspreads in the box-and-dot plots yields a similar observation. This difference in
spreads is pressing the limits of analysis of variance’s ability to withstand violation
of its basic assumptions. As long as the largest variance is no more than three times
the smallest, though, we are willing to go ahead and perform analysis of variance,
especially if the samples involved are not too small.
Figure
13.2 illustrates one possible result of a comparison of weights for the three
subsamples of projectile points from different parts of the Archaic period. Note
that Fig.
13.2 does not really illustrate the data presented in Table 13.1.Instead,it
illustrates one pattern that we might have seen. This pattern has been created by
maintaining the real shapes of all three subsamples but shifting their centers so that
they fall much closer together for purposes of discussion only. The stem-and-leaf
plots in Fig.
13.2 are drawn with letters standing for the different subperiods in order
to make it possible to see what happens when the three subsamples are combined,
as at the extreme right.
When we compare the overall sample of 127 projectile points in Fig.
13.2 to the
individual subsamples, we observe several things. First, in this result, all three sub-
samples look pretty much the same. All three have centers in about the same place.
All three have roughly similar spreads. Second, the spread of the overall sample
of 127 projectile points is similar to the spreads of the individual subsamples. And
third, the center of the overall sample of 127 projectile points is quite similar to the
centers of the individual subsamples. Despite some minor differences in shape, all
four stem-and-leaf plots are fairly similar. The sharpest difference is that the peak
in the stem-and-leaf for the overall sample is considerably higher than the peaks for
the individual subsamples. This should not be surprising, since the overall sample
has considerably more projectile points, but a spread not really larger than those of
the individual subsamples. Consequently they mount up higher at the peak.
A different possible result of such a comparison is illustrated in Fig.
13.3, and this
figure does, in fact, accurately reflect the data in Table
13.1. Comparing Fig. 13.3
with Fig. 13.2 reveals the nature of the differences. First, the three subsamples no
longer look pretty much the same. Their spreads continue to be roughly similar, but
their centers are clearly in different places. Second, the spread of the overall sample
is larger in Fig.
13.3 than in Fig. 13.2. It is no longer as close to the spreads of the
individual subsamples as it was in Fig.
13.2. While the Early Archaic subsample
has the largest spread, and this continues to be comparable to the spread in the
overall sample, the Middle Archaic and Late Archaic subsamples to have noticeably
narrower spreads than the overall batch. And third, the center of the overall sample,
while similar to the center in the Early Archaic subsample, is distinctly lower than
the center in the Middle Archaic subsample and distinctly higher than the center in
the Late Archaic subsample.
In sum, Fig.
13.3 shows that, as the centers of the subsamples vary from each
other, greater variation is introduced into the overall sample when the three sub-
samples are combined. Figure
13.2 illustrates a situation where all three subsamples
might well have been selected from populations with the same means. Figure
13.3
illustrates a situation where it is considerably more likely that the three subsamples
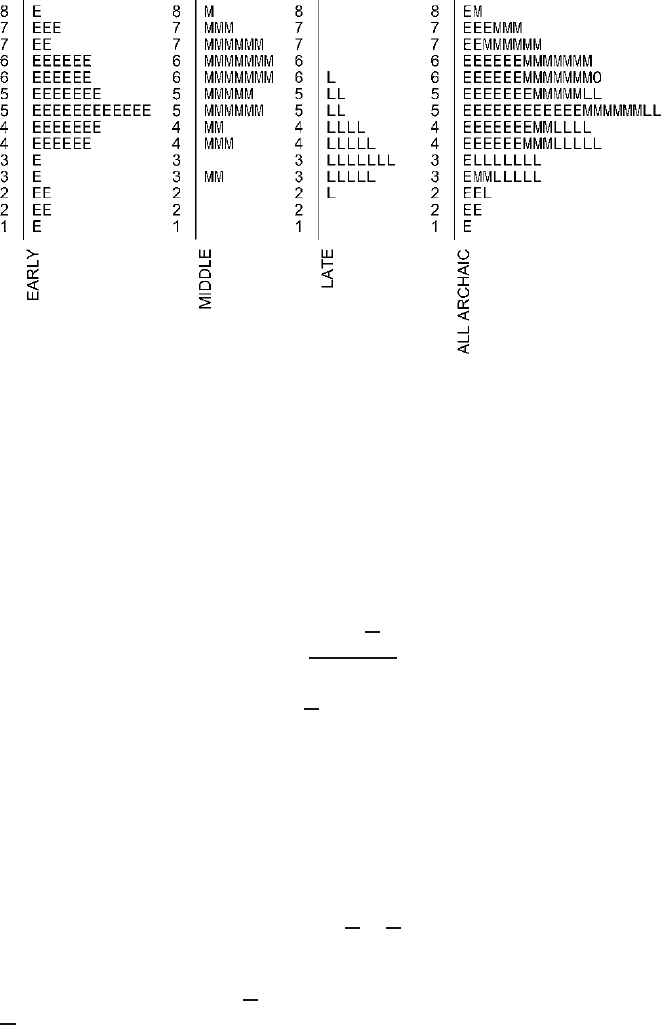
COMPARING MEANS OF MORE THAN TWO SAMPLES 171
Figure 13.3. Stem-and-leaf plots of projectile point weights by subperiod for the data presented in
Table
13.1.
were selected from populations with different means. Analysis of variance finds the
key to assessing these probabilities in a comparison between the variance observed
between subsamples on the one hand and the variance observed within subsamples
on the other. These two variances, between groups and within groups, are calculated
very much like the variances of ordinary batches of measurements.
Recall the equation for variance from Chapter
3:
s
2
=
∑
x −
X
2
n −1
The numerator of this fraction,
∑
x −
X
2
, is often referred to as the sum of squares
since it consists of the sum of the squares of the deviations from the sample mean
of all the elements in the sample. The denominator, n −1, is actually the number of
degrees of freedom, a term we did not use in Chapter
3, but which we have come
across since.
To calculate the between groups variance needed for analysis of variance we
must determine what the relevant sum of squares is and what the relevant number of
degrees of freedom is. The between groups sum of squares is
SS
B
=
∑
n
i
X
i
−X.
2
where SS
B
= the between groups sum of squares, n
i
= the number of elements in
the ith group (or subsample),
X
i
= the mean in the ith group (or subsample), and
X. = the mean of all the groups (taken together).

172 CHAPTER 13
In our example, there are three groups or subsamples, so i refers, in turn, to each
of the three groups, whose numerical indexes are given in Table
13.2. Thus
n
1
= 58 (the number of Early Archaic projectile points);
n
2
= 42 (the number of Middle Archaic projectile points);
n
3
= 37 (the number of Late Archaic projectile points;
X
1
= 53.67g (the mean Early Archaic projectile point weight);
X
2
= 60.45g (the mean Middle Archaic projectile point weight);
X
3
= 41.56g (the mean Late Archaic projectile point weight);
X. = 53.34g (the grand mean projectile point weight, that is, the mean of the
total sample including all periods).
Consequently,
SS
B
= 58(53.67 −53.34)
2
+ 42(60.45 −53.34)
2
+ 27(41.56 −53.34)
2
= 6.32 + 2123.19 + 3746.75
= 5876.26
The relevant number of degrees of freedom for this between groups sum of squares
is one less than the number of subsamples. For this example, there are three sub-
samples, so there are two degrees of freedom. Dividing the between groups sum of
squares by the number of degrees of freedom, we get
s
2
B
=
SS
B
d. f.
=
5876.26
2
= 2938.13
This figure is the between groups variance, often referred to as the between groups
mean square. It is the way we express the spread observed between the means of
the different groups for analysis of variance.
Analysis of variance seeks to compare the between groups variance just calcu-
lated to the within groups variance. This within groups variance, like the between
groups variance, involves dividing a sum of squares by the relevant number of
degrees of freedom. It amounts to pooling the separate variances of the subsam-
ples. The within groups sum of squares is obtained simply by multiplying each
subsample’s variance by one less than the number in the subsample and adding up
the results for all the subsamples:
SS
W
=
∑
(n
i
−1)s
2
i
where SS
W
= the within groups sum of squares, n
i
= the number of elements in
the ith group (or subsample) as before, and s
2
i
= the variance of the ith group (or
subsample).
Finding the variances of the subsamples in Table
13.2 gives us the following
values for s
2
i
: s
2
1
= 215.21, s
2
2
= 147.62, and s
2
3
= 76.74. Consequently, in our
example,

COMPARING MEANS OF MORE THAN TWO SAMPLES 173
SS
W
=(58 −1)(215.21)+(42 −1)(147.62)+(27−1)(76.74)
= 12266.97 + 6052.42 + 1995.24
= 20314.63
The relevant number of degrees of freedom for this within groups sum of squares is
the overall sample size minus the number of subsamples. In our example, the overall
sample size is 127, and there are three subsamples, so the within groups number of
degrees of freedom is 124. Dividing the within groups sum of squares by the number
of degrees of freedom, we get
s
2
W
=
SS
W
d. f.
=
20314.63
124
= 163.83
This figure is the within groups variance, often referred to as the within groups mean
square. It is the expression of the spread to be observed within the various groups
needed for analysis of variance.
Once the between groups variance and the within groups variance are calculated,
the analysis of variance is almost complete. It only remains to express these two
variances as a ratio:
F =
s
2
B
s
2
W
This F ratio in our example comes to
F =
2938.13
163.83
= 17.93
The F ratio can then be looked up in a table providing probabilities associated with
the different values of F. The probability associated with an F ratio of 17.93 for
2 degrees of freedom between groups and 124 degrees of freedom within groups
is 0.0000001. This means that there is only one chance in ten million of randomly
selecting three subsamples with the means and standard deviations that these have
from three populations whose means are the same. There is, then, a vanishingly
small probability that the differences observed between these three samples are
simply a consequence of the vagaries of sampling. Our results are extremely sig-
nificant. We have extremely high confidence that projectile points from different
periods really do have different mean weights.
Table 13.3. Example Computer Output for the Analysis of
Variance Example in This Chapter
ANALYSIS OF VARIANCE
SOURCE SUM OF SQUARES DF MEAN SQUARE F PROBABILITY
BETWEEN GROUPS 5880.6 2 2940.30 17.94 0.0000001
WITHIN GROUPS 20321.8 124 163.89
