Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

628 Part C Molecules

Table 42.2 Approximate tuning ranges for tunable lasers, cont.

Laser Wavelengths (nm) Notes

Color Centers: (F2+)/LiF 800–1040 cw: laser, Ar, Kr

/NaF 900–1050 cw: laser, Ar, Kr

/KCl:Tl 1400–1700 cw: laser, Ar, Kr, Nd/YA G

/KF 1300–1400 cw: laser, Ar, Kr, Nd/YAG

/NaCl 1400 –1600 cw: laser, Ar, Kr, Nd/YAG

/KCl 1600 –1700 cw: laser, Ar, Kr, Nd/YAG

/KBr 1700 –1900 cw: laser, Ar, Kr, Nd/YAG

/KCl:Li 2500–2900 cw: laser, Ar, Kr, Nd/YA G

/KCl:Na 1600 –1950 cw: laser, Ar, Kr, Nd/YA G

42.3 Interaction of Laser Light with Matter

42.3.1 Linear Absorption

The absorption cross section σ

for transition to the ﬁ-

nal state | f , when integrated over frequency ν,isgiven

theoretically by the leading ﬁrst-order perturbation of

the initial state |i in the electric dipole approxima-

tion



(ν) dν =4π



 f|



|i



, (42.26)

where the sum is over all charges e at distances r

 is a unit polarization vector, and

ν is the av-

eraged transition energy. Averaged over orientations

and summed over possible ﬁnal states, each elec-

tron contributes to the total integrated absorption cross

section one electron oscillator, πr

c ≈ 0.03 cm

−1

;

here, r

is the classical electron radius. Electronic ab-

sorption bands typically contain an oscillator strength

f = 0.01–0.5 of an “electron oscillator”, while weaker

vibrational transitions have f = 10

−6

–10

−4

in each

band.

For narrow lines with radiation of broader band

width ∆ν at ﬂux density J, the linear absorption rate

constant can be usefully estimated as (πr

c) fJ/∆ν.

42.3.2 Multiphoton Absorption

Second-order perturbation theory gives the theoretical

two-photon contribution to the absorption. An absorp-

tion cross section σ

(2)

for a photon of frequency ν

induced by an off-resonance monochromatic ﬁeld of fre-

quency ν

and photon ﬂux density J

. When integrated

over the frequency of the second photon, the second-

order cross section can be related to the dipole matrix

elements



(2)

(ν

,ν

dν

4π





r

r



−ν



(42.27)

where

r

=f|





|m ,

r

=m|





|i, (42.28)

and the sum is taken over intermediate states |m having

frequencies ν

and ν

for transitions to the initial and

ﬁnal states. The energy for the overall transition comes

from two photons; hence the two-photon resonance con-

dition ν

= ν

+ν

. A special case often occurs when

only one radiation frequency is used: then ν

= ν

,and

two-photon resonance is achieved when the energy of

the transition corresponds to twice the frequency of the

radiation ﬁeld.

This integrated, induced cross section is roughly

of the order α(πcr

)

/(ν

). Two-photon absorption

becomes comparable to the one-photon absorption with

off-resonance ﬁelds on the order of

≈

απcr

, (42.29)

or about 10

photons s

−1

−2

(10

−2

−1

for

typical green light).

Part C 42.3

Spectroscopic Techniques: Lasers 42.3 Interaction of Laser Light with Matter 629

Typical dipole-allowed molecular multiphoton ab-

sorption cross sections are ≈ 10

−58

s for two photons

and 10

−94

for three photons.

Multiphoton absorption was one of the ﬁrst ef-

fects explored with lasers. Two-photon absorption was

ﬁrst reported for inorganic crystals containing eu-

ropium ions [42.8]. Blue and ultraviolet ﬂuorescence

appeared in the interaction of red ruby laser light with

organic compounds [42.9–12]. Others observed two-

photon absorption directly [42.13, 14]. Selection rules

for multiphoton absorption are summarized by Mc-

Clain [42.15]; recent work is reviewed by Ashfold and

Howe [42.16].

Highly excited states may subsequently ionize in the

intense ﬁelds in a multiphoton ionization (MPI) process.

The ionization signal is often detected in a proportional

ionization cell. A low pressure cell containing the vapor

of a transition metal organometallic, such as iron car-

bonyl or ferrocene which photodissociates to give the

metal atom, may be used for wavelength calibration by

MPI.

42.3.3 Level Shifts

High radiation power causes resonant frequencies to

shift, responding to the ac Stark effect [42.17, 18]. Even

moderate ﬁelds, tuned near resonance, interact strongly

with an atom or small molecule, which undergoes rapid

excitation and stimulated emission at the characteristic

power dependent Rabi frequency,

Rabi

2πg

J . (42.30)

Fluorescence from such an interacting system has

a characteristic “head and shoulders” spectrum best

understood as radiation at the fundamental frequency

amplitude modulated at the Rabi frequency [42.19].

42.3.4 Hole Burning

Radiation at a particular frequency generally moves pop-

ulation out of states that absorb that radiation. Molecules

that interact resonantly with the radiation may also

spontaneously emit at different frequencies, thereby

ending in nonabsorbing states. This optical pumping

effect can make resonance features in an absorption

spectrum disappear at high power levels [42.20]. De-

pletion may appear as a “hole” in the absorption

spectrum [42.21]. Recently, interest has shifted to per-

manent “hole burning” as a method of information

storage in materials.

Hole burning is the basis for Doppler-free Lamb-

dip spectroscopy, in which only absorbing atoms or

molecules having little or no velocity component along

the axis of two counterpropagating beams are tem-

porarily depleted [42.22]. This technique is commonly

used for laser frequency stabilization, such as with the

iodine-locked He

−

Ne laser.

42.3.5 Nonlinear Optics

Multiplying

Nonlinear susceptibility of an optical medium can gen-

erate radiation at frequencies which are multiples of

the frequency of laser radiation passing through. Phe-

nomenologically, the second order polarization

2ν

= 

[2]

(42.31)

is given in terms of the second order nonlinear suscep-

tibility χ

[2]

, a third rank tensor, and the electric ﬁeld at

the fundamental frequency (see Chapt. 72). This nonlin-

ear susceptibility can range from 0.5–5pm/V for typical

materials used for frequency doubling. Typical materials

and their use are reviewed by Bordui and Fejer [42.23].

For a nonlinear process occurring over a length l

in a cylindrical region with Gaussian waist w

with

polarization P

on axis, the far ﬁeld ﬂux is given by

J(R,θ)=

4hc





sin

[(k

−k cos θ)l/2]

−k cos θ)



×exp



−k

sin

(θ)/2



. (42.32)

Here, n is the index of refraction and k the propagation

constant for the induced radiation, while k

is that for the

induced polarization, the vector sum of those of the orig-

inal radiation. When phase matched, k

−k cos θ = 0,

and the term in the brackets maximizes to (l/2)

The greatest difﬁculty is in selecting materials which

can be phase matched such that the relative phases of the

fundamental and overtone radiation propagate together

through the material; otherwise radiation at the higher

frequency generated at different places inside the ma-

terial destructively interfere. Phase matching is usually

achieved by either angle tuning of a birefringent crystal,

or by temperature tuning.

Only materials without a center of inversion in their

crystal structures have a second order nonlinear suscep-

tibility. All materials, including gases, will have a third

order nonlinear susceptibility χ

[3]

. This can be used

to generate third harmonics, especially in the vacuum

ultraviolet (VUV), where doubling materials are not

available [42.24, 25].

Part C 42.3

630 Part C Molecules

Mixing

The same materials that permit frequency doubling and

tripling also allow 3-wave and 4-wave frequency mixing.

The frequency matching conditions are, respectively,

±ν

= ν

±ν

= ν

. (42.33)

Tunable UV radiation may be generated by adding the

frequencies of a ﬁxed and tunable visible outputs. Tun-

able IR has been obtained by differencing ﬁxed and

tunable visible lasers. Mixing of radiation from an Ar

ion laser with that from a tuned R6G dye laser in lithium

iodate to produce tunable 2200–4600 nm radiation is

noteworthy.

Optical Parametric Oscillator

It is possible to reverse 3-wave mixing, generating two

frequencies whose sum is that of the input radiation. In

parametric generation, the output frequencies are given

by the phase match conditions. Both the desired fre-

quency and the secondary “idler” frequency must be

allowed to build up in the nonlinear medium. The idler

radiation is not present initially, but results from the fre-

quency mixing process itself. The process has many of

the characteristics of a laser oscillator, including that of

a gain threshold. This makes tuning of an optical para-

metric oscillator similar to that of a laser, but with more

degrees of freedom: now oscillation at two frequencies

must be attained simultaneously, along with the correct

phase matching of the nonlinear material [42.26].

42.3.6 Raman Scattering

It is possible to have one or more of the ﬁelds in a mixing

process belong to just polarization, rather than radiation.

The frequency additive case of multiphoton absorption

has already been consisdered; the frequency subtractive

case is Raman scattering.

Incoherent Raman Scattering

Radiation at a higher frequency can excite a lower fre-

quency vibration or rotation within a material, with

appearance of radiation at the frequency of the incident

radiation minus that of the absorption. The integrated

cross section for this effect is given by (42.27). However,

in this case the cross section is for emissionof the second

photon. The rate of spontaneous Raman emission is ob-

tained by multiplying (42.27) by the spectral ﬂux density

of the zero-point ﬁeld, 8πν

/

c. Typical vibrational Ra-

man cross sections for transparent molecules are about

−34

−1

in the blue–green (488 nm) [42.27].

Alternatively, energy can be extracted from an

excited state, with the inelastically scattered photon de-

parting with the sum of the incident frequency and that of

the deexcitation. The term “anti-Stokes” distinguishes it

from the more usual “Stokes” type of Raman scattering.

Coherent Raman Emission

The integrated cross section for emission stimulated at

the Raman frequency is given directly by (42.27).

A fourth-order mixing process that is less suscepti-

ble to saturation involves coherent anti-Stokes Raman

scattering (CARS). Two beams excite the material: the

difference of their frequencies corresponds to an excita-

tion of the material. Stimulated Raman scattering excites

the material, which then deexcites through an anti-

Stokes process, giving rise to a third, higher frequency

radiation ﬁeld. The phase is determinate, and the radia-

tion leaves the region of scattering as a beam [42.28].

If the incident radiation induces a Raman process

over a sufﬁciently long path, the stimulated Raman

process can be used for gain at both the Stokes and

anti-Stokes frequencies. Since spontaneous Raman pro-

cesses are proportional to the integrated cross section,

while gain in the stimulated Raman process is propor-

tional to the peak cross section, simple materials with

sharp, simple line spectra are most suitable for Raman

gain media. While Raman lasers have been produced

using vibrational excitation of organic liquids, currently

the most important technical application is for Raman

shifting the output of lasers, tunable or otherwise, to fre-

quencies which otherwise would be inaccessible. The

high pressure H

Raman shifter produces, at low pow-

ers, beams consisting almost entirely of well separated,

sharp lines shifted by 4160 cm

−1

from the pump beam;

at high powers, a series of Stokes and anti-Stokes bands

appear, each separated by 4160 cm

−1

from each other.

42.4 Recent Developments

One of the most exciting advancements in the past

decade in laser physics has been the generation of

optical frequency combs; and, more speciﬁcally, their

applicability in the domain of high-resolution laser spec-

Part C 42.4

Spectroscopic Techniques: Lasers References 631

troscopy. Basically, through a superposition process of

many continuous wave modes, a short train of fre-

quency spikes may be produced from a mode-locked

laser [42.29] (see also Sect. 30.1.5). These spikes are

equally spaced and are referred to as a frequency comb.

The frequency ω

of the n

cavity mode may be ex-

pressed as

= nω

+ω



, (42.34)

where ω

is characteristic of the laser and ω



is a fre-

quency offset due to the difference between the phase

and group velocity of the superposed waves.

The microwave frequencies ω

and ω



are deter-

mined through the use of nonlinear optics. Once these

two parameters are determined, any unknown optical

frequency ω

may be measured by recording the beat fre-

quency between it and the closest comb frequency. This

technique gives experimenters a high-precision method

for the spectroscopic determination of such fundamen-

tal quantities as the ﬁne structure constant, the Rydberg

constant, and the Lamb shift [42.30, 31].

Text and references updated by Mark M. Cassar

References

42.1 A. Einstein: Phys. Z. 18,121(1917)

42.2 H. Kogelnik, T. Li: Proc. IEEE 54, 1312 (1966)

42.3 J. T. Verdeyen: Laser Electronics, 3rd edn. (Prentice

Hall, Englewood Cliffs 1994)

42.4 O. Svelto: Principles of Lasers (Plenum, New York

1976)

42.5 R. Wallenstein, T. W. Hänsch: Opt. Commun. 14,353

(1975)

42.6 E. P. Ippen, C. V. Shank, A. Dienes: Appl. Phys. Lett.

21,348(1972)

42.7 R. K. Jain, C. P. Ausschnitt: Opt. Lett. 2, 117 (1978)

42.8 W. Kaiser, C. G. B. Garrett: Phys. Rev. Lett. 7, 229

(1961)

42.9 W. L. Peticolas, J. P. Goldsborough, K. E. Rieckhoff:

Phys. Rev. Lett. 10, 4345 (1963)

42.10 W. L. Peticolas, K. E. Reickhoff: J. Chem. Phys. 39,

1347 (1963)

42.11 S. Singh, B. P. Stoicheff: J. Chem. Phys. 38, 2032

(1963)

42.12 S. Z. Weisz, A. B. Zahlen, J. Gilreath, R. C. Jarnagin,

M. Silver: J. Chem. Phys. 41, 3491 (1964)

42.13 J. J. Hopﬁeld, J. M. Warlock, K. Park: Phys. Rev. Lett.

11,414(1963)

42.14 B. Staginnus, D. Frölich, T. Caps: Rev. Sci. Instrum.

39, 1129 (1968)

42.15 W. M. McClain: Acc. Chem. Res. 7,129(1974)

42.16 M. N. Ashfold, J. D. Howe: Ann. Rev. Phys. Chem.

45, 57 (1994)

42.17 H. J. Carmichael, D. F. Walls: J. Phys. B 9, 1199

(1976)

42.18 L.-P. Li, B.-X. Yang, P. M. Johnson: J. Opt. Soc.

Am. 2,748(1985)

42.19 B. R. Mallow: Phys. Rev. 188, 1969 (1969)

42.20 L. J. Rothberg, D. P. Gerrity, V. Vaida: J. Chem. Phys.

75, 4403 (1981)

42.21 S. Völker: Ann. Rev. Phys. Chem. 40, 499 (1989)

42.22 W. R. Bennett Jr.: Phys. Rev. 126, 580 (1962)

42.23 P. F. Bordui, M. F. Martin: Ann. Rev. Mater. Sci. 23,

321 (1993)

42.24 A. Kung: Opt. Lett. 8, 24 (1983)

42.25 J. Bokor, P. Bucksbaum, R. Freeman: Opt. Lett. 8,

217 (1983)

42.26 J. Falk, J. M. Yarbourough, E. O. Ammann: IEEE J.

Quantum Elec. 7,359(1971)

42.27 C. M. Penney, R. L. St. Peters, M. Lapp: J. Opt. Soc.

Am. 64,712(1974)

42.28 P. R. Regnier, J. P. Taran: Appl. Phys. Lett. 23,240

(1973)

42.29 T. Udem, R. Holzwarth, M. Zimmerman, C. Goble,

T. Hänsch: Topics Appl. Phys. 95, 295 (2004)

42.30 J. M. Hensley: A precision measurement of the ﬁne

structure constant. Ph.D. Thesis (Stanford Univer-

sity, Stanford 2001)

42.31 B. de Beauvoir, C. Schwob, O. Acef, L. Jozefowski,

L. Hilico, F. Nez, L. Julien, A. Clairon: Eur. Phys. J.

D 12, 61 (2000)

Part C 42

633

Spectroscopic

43. Spectroscopic Techniques:

Cavity-Enhanced Methods

Cavity enhanced spectroscopy (CES)methodology

provides a much higher degree of sensitivity

than that available from conventional absorption

spectrometers. The aim of this chapter is to

present the fundamentals of the method, and the

various modiﬁcations and extensions that have

been developed. In order to set the stage, the

limitations of traditional absorption spectrometers

are ﬁrst discussed, followed by a description of

cavity ring-down spectroscopy (CRDS), the most

popular CES embodiment. A few other well-known

CES approaches are also described in detail. The

chapter concludes with a discussion of recent work

on extending CRDS to the study of liquids and

solids.

43.1 Limitations

of Traditional Absorption Spectrometers 633

43.2 Cavity Ring-Down Spectroscopy ............ 634

43.2.1 Pulsed Cavity Ring-Down

Spectroscopy ............................ 634

43.2.2 Continuous-Wave Cavity

Ring-Down Spectroscopy

(CW-CRDS) ................................ 635

43.3 Cavity Enhanced Spectroscopy............... 636

43.3.1 Cavity Enhanced Transmission

Spectroscopy (CETS) .................... 637

43.3.2 Locked Cavity Enhanced

Transmission Spectroscopy

(L-CETS).................................... 638

43.4 Extensions to Solids and Liquids ........... 639

References .................................................. 640

43.1 Limitations of Traditional Absorption Spectrometers

An absorption spectrometer measures the difference in

intensity between the incident light intensity I

and the

transmitted light intensity I(x,λ). Beer’s law relates the

absorbed light to the sample absorption α(λ)

I(x,λ)= I

−α(λ)x

, (43.1)

where λ is wavelength, and x is path length. Absorption

is related to concentration C through the extinction coef-

ﬁcient ε(λ) namely α(λ) = Cε(λ). Typically, a spectral

feature, called an absorption peak, of the target species

is measured in order to obtain its concentration. The

performance of a spectrometer has two ﬁgures of merit:

sensitivity and selectivity.

Sensitivity is the smallest detectable change in one

centimeter of path length that a spectrometer can meas-

ure during one second. If many measurements can be

made within a second, averaging may be used to further

improve (by a factor of the square root of the number

of measurements or the square root of the data acquisi-

tion rate) the achievable sensitivity. Sensitivity has units

of cm

−1

−1/2

. Sensitivity can also be quantiﬁed us-

ing the minimum detectable absorption loss (MDAL),

i. e., the normalized standard deviation of the small-

est detectable change in absorption (units of cm

−1

Equation (43.1) shows that the sensitivity of a spectrom-

eter depends not only on the light path length through

the sample, but also on the intensity noise of the light

source.

Selectivity is the ability of a spectrometer to distin-

guish between two different species absorbing at similar

wavelengths. The instrument must be able to resolve

the different spectral lines. Thus, selectivity depends on

spectral resolution, which has units of frequency (MHz),

wavelength (nm), or wavenumbers (cm

−1

Traditional spectrometers, such as non-dispersive in-

frared (NDIR), and Fourier Transform infrared (FTIR),

use incoherent thermal light sources. For both tech-

niques, the physical length of their sample chamber

limits their sensitivity. Some devices try to fold the

light path several times through the sample cham-

ber in order to improve sensitivity, but this approach

encounters physical size and mechanical stability lim-

itations. Typical MDAL are in the 10

−5

−1

range.

These instruments therefore rely on measuring the

strongest absorption transitions available, which are

found in the mid-infrared range (3 to 12 µm). Often,

however, the strongest transitions overlap with features

of other species found in the sample mixture. The in-

strument performance becomes a sensitivity-selectivity

tradeoff.

Part C 43

634 Part C Molecules

Laser-based optical detection methods, called tun-

able diode laser absorption spectroscopy (TDLAS),

circumvent some of these problems by exploiting the co-

herent nature of laser light. A tunable continuous-wave

laser source brings two beneﬁts:

•

A narrow linewidth, which allows high spectral res-

olution scans to be performed, and

•

Low spatial beam divergence, which allows it to be

folded hundreds, if not thousands of times.

By transmitting laser light having a small beam

size over long distances, multi-pass cells can be

designed to achieve up to a kilometer of path

length enhancement. Multi-pass cell laser spec-

troscopy systems have demonstrated MDAL down

to 10

−9

−1

. However, such instruments still re-

main limited by laser intensity ﬂuctuations and

interference fringes. Moreover, standard multi-pass

techniques do not provide an absolute optical loss

measurement.

43.2 Cavity Ring-Down Spectroscopy

Cavity ring-down spectroscopy (CRDS)isamore

recently developed TDLAS approach that replaces

a multi-pass cell with a stable optical resonator, called

the ring-down cavity (RDC). CRDS is based on the prin-

ciple of measuring the rate of decay of light intensity

inside the RDC. The transmitted wave decays exponen-

tially in time. The decay rate is proportional to the total

optical losses inside the RDC.

In a typical CRDS setup, light from a laser is ﬁrst

injected into the RDC, and is then interrupted. The

circulating light inside the RDC is both scattered and

transmitted by the mirrors on every round-trip, and can

be monitored using a photodetector placed behind one

of the cavity mirrors. The decay constant, also called

the ring-down time τ is then measured as a function of

laser wavelength to obtain a spectrum of the cavity op-

tical losses. Detailed mathematical treatments of CRDS

can be found in [43.1]. A simple derivation is presented

here.

For a given wavelength λ the transmitted light I(t,λ)

from the RDC is given by

I(t,λ)= I

−

τ(λ)

, (43.2)

where I

is the transmitted light at the time the light

source is shut off, and τ(λ) is the ring-down time

constant. The total optical loss inside the cavity is

L(λ) =

[

cτ(λ)

]

−1

where c is the speed of light. The

total optical loss comprises the empty cavity optical loss

and the sample optical loss. CRDS provides an abso-

lute measurement of these optical losses. The empty

cavity (round-trip) optical loss L

empty

(λ) comprises

the scattering and transmission losses of the mirrors.

In general, better mirrors provide lower empty cavity

losses and higher sensitivity. The sample (round-trip)

optical loss is A(λ) = α(λ)l

where l

is the cavity

round-trip length, and is simply the difference between

total cavity losses and empty cavity losses, namely

A(λ) = L(λ) − L

empty

(λ). Once the absorption spec-

trum α(λ) of the sample has been measured, then the

sample concentration can be readily computed using the

absorption cross section and lineshape parameters.

The MDAL for a CRDS system is deﬁned by

min

eff



∆τ



(43.3)

where (∆τ/τ) is called the shot-to-shot noise of the sys-

tem. The effective path length of a CRDS measurement

is l

eff

= cτ. For typical RDC mirrors having a reﬂectivity

of 99.995%, and scattering losses of less than 0.0005%,

the path length enhancement can exceed 20 000. For

a 20 cm long sample cell, the effective path length is

8 km, which exceeds the best performance of multi-pass

spectroscopy by a factor of three, based on effective

path length alone. A good CRDS system can achieve

a shot to shot variation of 0.03%, leading to a MDAL

of 4 × 10

−10

−1

. Note also that the CRDS measure-

ment is not dependent on either the initial intensity of

the light inside the cavity, provided that the signal has

a sufﬁcient signal to noise ratio at the detector, or on the

physical sample path length like traditional absorption

spectroscopy. Moreover, CRDS can use laser sources

having narrow linewidths and achieving high spectral

resolution.

CRDS can resolve all three limitations of absorp-

tion spectroscopy, namely sensitivity, selectivity, and

dependence on intensity noise of the light source [43.1].

CRDS has been implemented using many different ap-

proaches. This chapter will discuss several commonly

used variations on the CRDS technique.

43.2.1 Pulsed Cavity Ring-Down

Spectroscopy

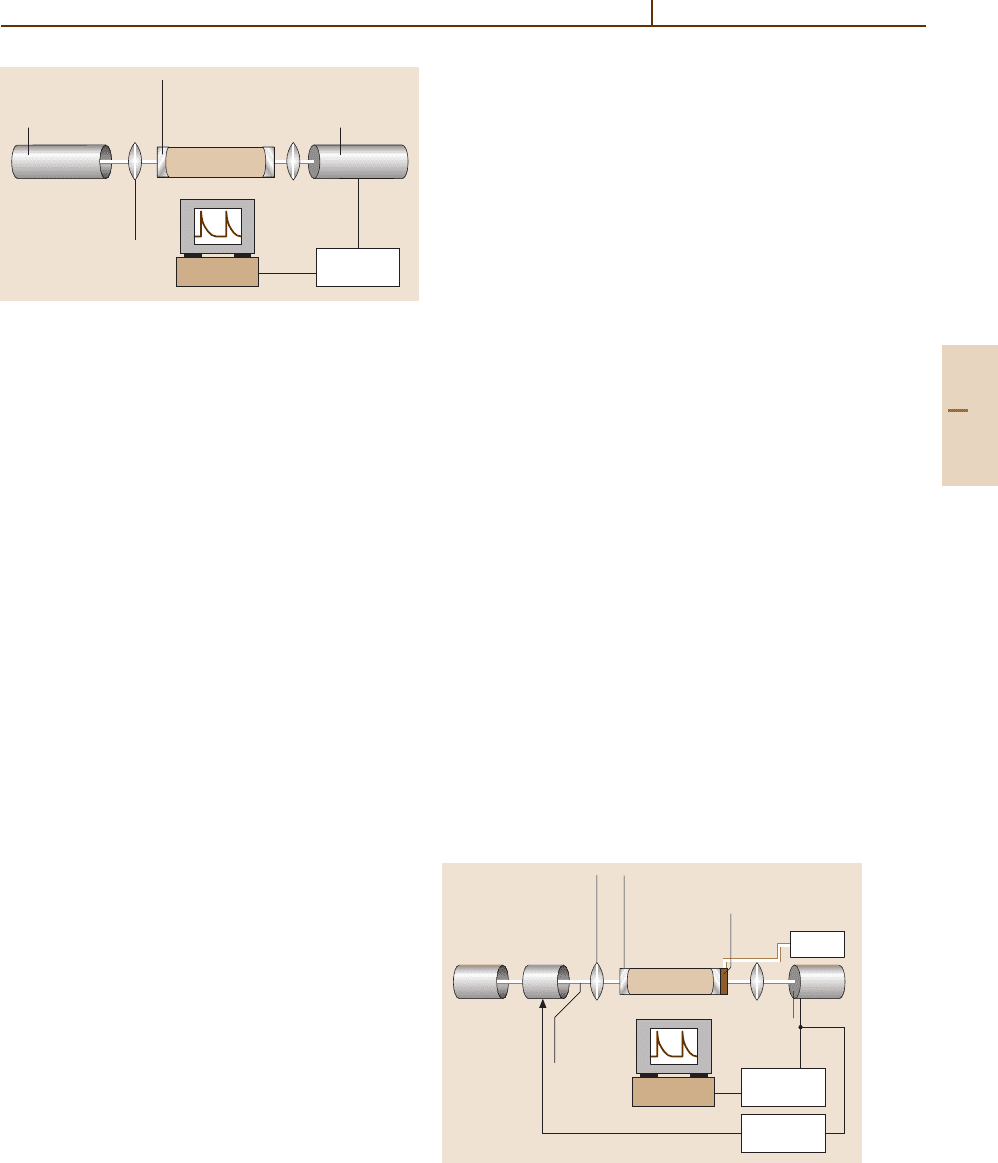
Early implementations of CRDS used pulsed lasers

sources (P-CRDS) [43.2]. A typical P-CRDS setup

Part C 43.2

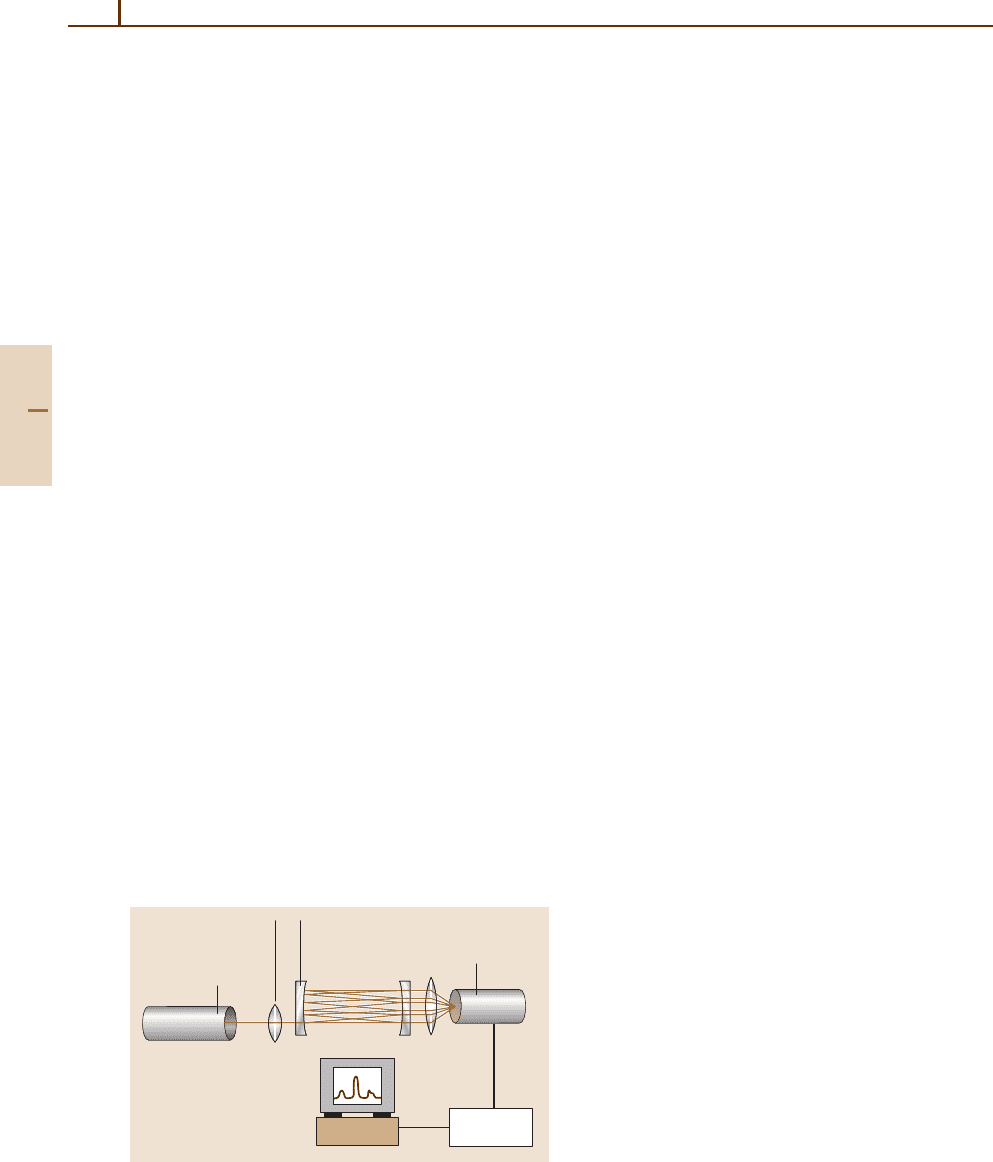
Spectroscopic Techniques: Cavity-Enhanced Methods 43.2 Cavity Ring-Down Spectroscopy 635

High reflectivity mirrors:

Cavity/ Sample chamber

Pulsed laser

Mode-matching

optics (optional)

Detector

A/D

Converter

Fig. 43.1 Typical P-CRDS setup

is shown in Fig. 43.1. Today, CRDS has been imple-

mented in the broadest possible range of wavelengths,

from the UV (216 nm) to the mid-infrared (10 µm).

Because of its experimental simplicity, P-CRDS has

become a widespread tool for chemists and spectro-

scopists, ﬁnding applications in the measurement of

predissociation dynamics, photolysis products, radiative

lifetimes, aerosols or soot detection, temporal imaging,

overtone vibrational spectroscopy, and kinetic studies.

Typical P-CRDS sensitivity is 1 × 10

−9

−1

−1/2

P-CRDS methods have also been combined with

other detection methodologies. Variations on P-CRDS

include:

•

Fourier-transform (FT) P-CRDS [43.3], where an

RDC is excited with a broadband source and time-

resolved FT scans of the RDC output waveform are

taken. Inversion of the interferogram then produces

time-dependent ring-down waveforms at all resolved

frequencies within the source wavelength range.

•

Polarization P-CRDS [43.4], where the spectral

splitting induced by the magnetic ﬁeld is observed

from the difference of the ring-down spectra of the

two orthogonal polarizations.

•

Pulse-stacked P-CRDS [43.5], where the length of

the RDC is set so that pulses from a very high repe-

tition rate pulsed source coherently add together,

which increases the effective cavity light through-

put to yield improved detection of the ring-down

waveform.

Spectral resolution and sensitivity of P-CRDS are,

however, limited by the use of short-pulse lasers. The

effects of pulsed laser bandwidth on spectral resolu-

tion of P-CRDS have been studied extensively and have

led to system designs where only a single longitudi-

nal and transverse mode of the RDC is excited [43.6].

However, single-mode P-CRDS is difﬁcult to implement

experimentally, and still has limited sensitivity because

the laser pulse is substantially attenuated by the RDC

mirrors at the cavity output. The requirement for im-

proving CRDS sensitivity by reducing the variability in

the measurement of the decay constant from shot to shot

with single-mode excitation, and improving the light

transmission through the cavity to increase the signal to

noise ratio of the decay waveform on the detector, pro-

vided the catalyst to implement continuous wave (CW)

lasers in CRDS.

43.2.2 Continuous-Wave Cavity Ring-Down

Spectroscopy (CW-CRDS)

CW lasers have narrow linewidths (< 50 MHz) and can

be tuned in small spectral increments (< 50 MHz) to

achieve high spectral resolution with excellent wave-

length reproducibility. Moreover, owing to their narrow

linewidths, they are better suited for efﬁciently coupling

into a single mode of a high ﬁnesse RDC, thereby reduc-

ing shot-to-shot variations in measured ring-down decay

constant. Furthermore, they can be directly modulated,

thereby allowing higher data repetition rates, leading in

turn to improved sensitivity.

The ﬁrst efforts in CW-CRDS involved optically

locking a laser diode to a high-ﬁnesse cavity, but the per-

formance was limited because the laser diode would drift

andlocktodifferentRDC modes. The use of sufﬁcient

optical isolation and an external optical switch resolved

this issue. The most common approach used today is

to sweep a RDC mode through the emission proﬁle of

a diode laser, and shut the laser off with an acousto-optic

modulator (AOM)(Fig.43.2) when sufﬁcient light is in-

jected into the cavity [43.7]. Numerous variations on this

approach exist. For example, CW-CRDS can be imple-

mented by rapidly sweeping the cavity mode into and

High reflectivity mirrors:

Cavity/ Sample chamber

CW laser

Mode-matching

optics (optional)

Detector

A/D

Converter

Driver

AOM

Threshold

trigger

First-order

deflected

beam

PZT actuator

Fig. 43.2 Typical CW-CRDS setup

Part C 43.2

636 Part C Molecules

out of resonance with the laser. The simplest approach

is to sweep the laser wavelength into and out of reson-

ance with a cavity mode and directly modulate the laser

source current [43.8]. The most popular CW lasers used

today are distributed feedback (DFB) diode lasers.

In most CW-CRDS embodiments, the ring-down

cavities are linear, i. e., consist of two mirrors. Ring

resonators (e.g., triangular or bow-tie cavities) can also

be used. Ring cavities provide the beneﬁts of mini-

mizing optical feedback and eliminating the need for

extensive isolation or frequency shifting of the laser

source. Moreover, ring resonators break the frequency

degeneracy between cavity modes having orthogonal po-

larizations, effectively creating two coupled resonators

having high and low ﬁnesse, respectively. The low ﬁ-

nesse cavity can be used to lock the laser to a single

cavity mode, while the high ﬁnesse cavity can be used

for CRDS.TheAOM acts as both a frequency-shifter

and an on-off switch. This method was used to demon-

strate the highest CRDS sensitivity achieved to date,

namely 1.0×10

−12

−1

−1/2

[43.9].

Prism-based, rather than mirror-based cavities

have also been used [43.10]. Such cavities comprise

two prisms whose intra-cavity facing angles are at

Brewster’s angle, and whose extra-cavity facing angles

are such that total internal reﬂection occurs, and results

in unit reﬂectivity. One of the prisms has a curved facet

to create a stable optical resonator. The purpose of this

design is to extend operation over a much broader range

of wavelengths than can be achieved using dielectric

coatings. Currently, high reﬂectivity mirrors are limited

in bandwidth to about ±15% of their center wavelength.

CW-CRDS has been applied over a wide range of

wavelengths. It has been used for medical breath an-

alysis, trace gas detection in environmental and process

control applications, and isotopic analysis. In the near-

infrared, CW-CRDS systems achieve sensitivities of

−11

−1

−1/2

, and a concentration measurement

repeatability of 1 part in 5000. Similar performance

in the mid-infrared (3 µm) resulted in the detection of

parts-per-trillion ethylene concentrations [43.11].

Extensions of the basic CW-CRDS technique have

also been developed:

•

Phase-shifted CW-CRDS [43.12]: the phase shift

accrued by a sinusoidally modulated CW laser is

measured for both an empty RDC and one having

a sample. The concentration is deduced from these

two measurements.

•

Heterodyne CW-CRDS [43.13]: enhances the power

in the ring-down decay waveform by mixing with

a local oscillator. For example, the local oscillator

can be the orthogonal polarization used to lock the

laser to the RDC, or can be the reﬂected signal from

the RDC when laser is frequency-shifted (by the

local oscillator frequency) off resonance from the

RDC mode. Heterodyne CRDS can approach the

shot-noise limit.

•

V-cavity CW-CRDS [43.14]: a three-mirror V-

shaped RDC is exploited to achieve consistent

repetitive optical locking of a DFB diode laser to

a single cavity mode, thereby signiﬁcantly enhan-

cing light throughput.

CW-CRDS is now maturing to a level of robust-

ness and reliability that it can be commercially deployed

in industrial applications, where the sensitivity require-

ments can no longer be met by FTIR, NDIR,orgas

chromatography.

43.3 Cavity Enhanced Spectroscopy

Most CRDS systems capture the ring-down waveform

using a digital oscilloscope. The Levenberg–Marquardt

(LM) method produces the optimal ﬁt, so that LM

methods have become the de facto “gold standard” in

CRDS [43.15]. However, the LM algorithm can require

multiple iterations, thereby limiting the data acquisition

times to several hundred Hz. Fast-ﬁtting algorithms that

closely approximate the LM ﬁt, but allow data acquisi-

tion rates up to 10 kHz have recently gained widespread

deployment [43.16]. Today, the data acquisition rates are

no longer limited by the back-end numerical ﬁt. Rather,

the speed of CRDS systems is limited by the speed of

laser modulation itself.

Cavity enhanced spectroscopy (CES) was developed

in an effort to simplify CRDS and eliminate the require-

ment for digitization of a time-domain signal and laser

modulation. CES has many different implementations.

All CES methods are based on the principle that the build

up of intracavity power, and hence cavity throughput, de-

pends on intracavity losses, which include absorption by

a sample. CES involves measuring the steady-state trans-

mission through a cavity as a function of wavelength

in order to determine changes in integrated transmitted

intensity caused by the absorbing species.

For a cavity having two mirrors of intensity re-

ﬂectivity, R, and length, L, the effective steady-state

Part C 43.3

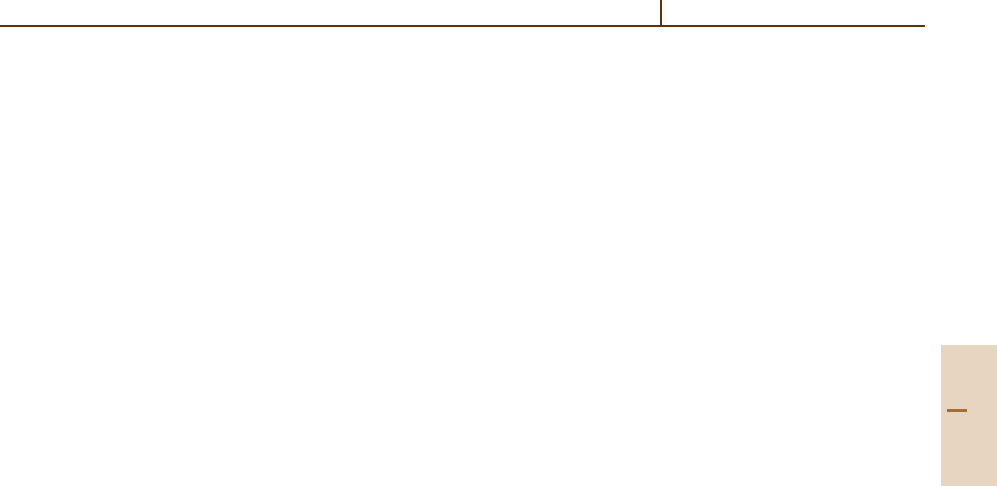
Spectroscopic Techniques: Cavity-Enhanced Methods 43.3 Cavity Enhanced Spectroscopy 637

path length is L

eff

= L/(1 − R). If an absorbing gas

is present, the reﬂectivity will be “reduced” by the

Beer–Lambert factor e

−αL

namely R



= Re

−αL

so that

one can effectively relate the ratio R



/R to the Beer–

Lambert ratio I/I

for a single pass. The steady state

transmitted laser intensity for such a cavity is given by

I = I

[

2(1 − R)

]

−1

where T is the intensity trans-

missivity I

is the laser intensity, and C

is the coupling

efﬁciency in the cavity mode. Thus, for an absorbing gas,

the change in transmitted intensity at a given wavelength

is:

∆I/I = GA

(

1 + GA

)

−1

, (43.4)

where A = 1 − e

−αL

and G = R/(1 − R) so that for

αL  1, (∆I/I) ≈ GA≈ GαL. This latter relation has

been interpreted as a linear response in absorption loss,

multiplied by an effective cavity “gain” of R/(1 − R),

i. e., the absorbance is measured over the effective length

of the cavity which corresponds to the number of cav-

ity passes occurring within the cavity ring-down time

constant. Note that the transmitted power level will

be attenuated by the mirror transmissivity, T,sothat

these methods are limited by laser power and detector

sensitivity.

Because CES techniques measure transmitted light

intensity, they are no longer immune to laser intensity

noise. Furthermore, when the absorbance becomes com-

parable to the cavity loss, the sensitivity improvement of

CES saturates, as the sample absorption begins to domi-

nate the effective number of cavity passes. Note that for

this case, the effective path length becomes a function

of the sample concentration, which underlines another

limitation of CES: this technique is not independent of

the cavity length and hence depends on cavity align-

ment. Moreover, CES systems are not self-calibrated

to the species extinction coefﬁcient, and therefore re-

quire calibration against a known sample concentration,

or against the absolute cavity loss, often measured us-

ing CRDS. Finally, it should be noted that the rate of

data collection in CES is limited by the RDC time con-

stant, because the cavity acts like a single-pole, low pass

ﬁlter having a 3 dB frequency of (2πτ)

−1

which can

range from 5 to 50 kHz. Unlike CRDS, CES does not re-

quire fast digitization of the decay waveform followed

by a non-linear ﬁt, so that the data acquisition hardware

can be a much slower, less expensive A/D converter and

spectral data can be acquired almost instantaneously.

Five distinguishable variants of CES have been

developed and are discussed. The ﬁrst three

methods, called cavity enhanced transmission spec-

troscopy (CETS), ﬁnd their origins in CRDS.These

methods are cavity enhanced absorption spectroscopy

(CEAS) [43.17], integrated cavity output spectroscopy

(ICOS) [43.18], and off-axis ICOS [43.19]. For these

three approaches, the laser intensity is no longer inter-

rupted to observe a “ring-down event”, although the

path length enhancing properties of the RDC remain.

More sensitive CES methods involve locking the laser

to the cavity mode resonance. These will be referred to as

locked cavity enhanced transmission spectroscopy and

have two variations: locked cavity enhanced transmis-

sion spectroscopy (L-CETS) [43.20] and noise-immune,

cavity-enhanced optical heterodyne molecular spec-

troscopy (NICE-OHMS) [43.21].

43.3.1 Cavity Enhanced Transmission

Spectroscopy (CETS)

CETS has been implemented using several variations,

all of which are based on measuring the time-integrated

transmission through a high ﬁnesse RDC as function of

wavelength. As stated earlier, the transmitted light pro-

vides an effectively enhanced path length to any sample

absorption inside the cavity. The transmitted light inten-

sity in all CETS approaches is a small fraction [about

(1 − R)] of the incident intensity, which reduces the

signal to noise on detection, so that averaging is re-

quired. All CETS approaches are also dependent on laser

intensity noise and sample path length.

The trade-off in using a high ﬁnesse cavity is that in

steady state, its transmission is a non-uniform function

of wavelength, and consists of a series of sharp cav-

ity mode peaks, namely the transverse and longitudinal

modes. This transmission pattern repeats itself periodic-

ally every free spectral range (FSR). The density of the

mode spacing is a function of the cavity design: round-

trip length and mirror radius of curvature. The quality

of mode matching between the laser and the RDC deter-

mines the number of modes into which light can couple

efﬁciently.

CEAS is the simplest CETS approach: the laser,

coupled through a RDC, is tuned in wavelength over

the absorption feature of interest, and the integrated

cavity transmission is measured as a function of wave-

length [43.17]. The cavity length is free-running (neither

modulated nor locked to the laser). In order to minimize

the non-uniformity of cavity transmission, CEAS ex-

ploits cavity geometries such that the inherent mode

structure is as dense as possible. No mode-matching is

employed, so that laser light is coupled into as many

modes as possible. The laser is scanned multiple times

over the cavity modes in order to time average over

Part C 43.3

638 Part C Molecules

the unstabilized cavity length. Extensive averaging can

be required to achieve reasonable performance. The

residual mode structure of the cavity can be signiﬁcant

and produces intensity modulation in the spectrum. Typ-

ically, the laser linewidth is larger than the individual

cavity mode resonances, so that the output can be very

noisy. CEAS does appear to have mechanical stability

advantages, in that a cavity length change or deforma-

tion is in fact desirable to randomize the excited modes

over wavelength. Typical sensitivities of CEAS range

from are 5 × 10

−7

−1

−1/2

ICOS tries to achieve uniform transmission through

the RDC by systematically disrupting the cavity

mode resonances, in order to recover the frequency-

averaged response of the cavity as a function of

wavelength [43.18]. RDC length modulation was im-

plemented by either moving one of the cavity mirrors

using a piezo-electric transducer (PZT), or by slightly

modulating the angle of injection in the cavity using

a PZT-driven mirror mount. When the laser is scanned

over the desired wavelength range with only the RDC

modulation sweeping the modes (5 to 10 free spectral

ranges), the resulting absorption spectra show an inten-

sity modulation of about 10%. This intensity modulation

results from a periodic non-uniformity in the mirror

movement at the turning points of the PZT modulation,

where the increased overlap time between the cavity

mode and laser produces a higher transmitted light in-

tensity. In order to eliminate this intensity modulation,

the laser wavelength is frequency modulated simultane-

ously. The typical sensitivity of ICOS approach is about

2×10

−7

−1

−1/2

A third approach, called off-axis ICOS, resolves the

cavity transmission uniformity problem of CEAS,and

eliminates the need for modulation of ICOS.Inoff-

axis ICOS, shown in Fig. 43.3,theRDC is aligned so

as to generate a set of spatially separated reﬂections

High reflectivity mirrors:

Cavity/ Sample chamber

CW laser

Mode-matching

optics (optional)

Detector

Integrator

Fig. 43.3 Typical off-axis ICOS setup

within the cavity that eventually satisfy the re-entrant

condition [43.19]. Furthermore, the mirrors are slightly

astigmatized, which results in Lissajous spot patterns

on the mirrors. The combination of this alignment and

slight astigmatism signiﬁcantly reduces the RDC mode

degeneracy. As a result, the cavity mode spacing can

become smaller than the cavity mode width, the cavity

transmission appears to become largely frequency inde-

pendent, or “white”. Thus, the RDC provides path length

enhancement, without introducing intensity noise in the

transmitted spectrum. However, increasing the number

of spots on the mirrors usually requires larger mirrors

(e.g., 2 inches for off-axis ICOS versus 0.5 inches for

CRDS), which in turn results in a larger cavity (sample)

volume. In cases of low sample ﬂow, sample chamber

ﬁlling times can limit the measurement time. Moreover,

the system is now dependent on the mechanical sta-

bility of the cavity and the laser to cavity alignment.

The best off-axis ICOS sensitivity achieved to date is

3×10

−11

−1

−1/2

and is comparable to CW-CRDS.

43.3.2 Locked Cavity Enhanced

Transmission Spectroscopy (L-CETS)

An alternative approach (L-CETS) achieves higher sen-

sitivity by locking the laser frequency to a single cavity

resonance and then scanning the cavity over the absorp-

tion feature of interest [43.20]. In this case, the cavity

throughput becomes uniform across the entire spectral

scan, and the cavity transmission increases to the maxi-

mum theoretical value, leading to better signal to noise

at the detector than CETS approaches. Laser wavelength

jitter at high frequencies, which cannot be compensated

by the locking control loops, will lead to increased noise

in the spectral scans. In order to lock the laser and cav-

ity together robustly, the laser linewidth typically cannot

exceed the cavity mode resonance linewidth, so that for

a high ﬁnesse sample cavity, the laser choice can be

limited. Sensitivities of 10

−11

−1

−1/2

have been

demonstrated using L-CETS.

The NICE-OHMS technique was developed to over-

come the dependence of L-CETS on laser wavelength

jitter [43.21]. NICE-OHMS combines the beneﬁts of

frequency modulation (FM) spectroscopy with the path

length enhancements of a high ﬁnesse optical resonator.

The technique is called “noise immune”, because it does

not depend on the quality of the laser and cavity lock.

Effectively, it is immune to laser frequency noise al-

though residual amplitude modulation can reduce the

performance. NICE- OHMS sensitivity depends on the

transmitted laser power, the efﬁciency and bandwidth of

Part C 43.3