Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


430 Part B Atoms
or
µ = gµ
N
i . (28.4)
In (28.4), µ
N
= e /(2m
p
) is the nuclear magneton, de-
fined in analogy with the Bohr magneton, and i is
the spin quantum number of the nucleus defined by
I
2
= i(i + 1)
2
and I
z
=−i ,... ,(i − 1) , i ,where
I
z
is the spin projection. However, in some publications
moments of nucleons are expressed in terms of the Bohr
magneton with a corresponding change in the definition
of the g-factor.
One of the most precise tests of QED is the compari-
son of theory and experiment for the electron magnetic
moment anomaly; the current status of this comparison
is given in this section.
The electron magnetic moment is proportional to
g
e
=−2(1 + a
e
), (28.5)
where the anomaly a
e
characterizes the deviation of
the g-factor from the Dirac value of g
e
(Dirac) =−2.
Measurement of the anomaly by the University of Wash-
ington group has yielded values for the electron and
positron given respectively by [28.4]
a
e
−
(exp) = 1 159 652 188.4 (4.3) ×10
−12
, (28.6)
a
e
+
(exp) = 1 159 652 187.9 (4.3) ×10
−12
, (28.7)
which yield the mean value
a
e
(exp) = 1 159 652 188.3 (4.2) ×10
−12
, (28.8)
based on the analysis described in [28.1]. This analysis
assumes that CPT invariance holds for the electron–
positron system.
The same experiment has provided a precision com-
parison of the electron and positron g-factors
g
e
−
g
e
+
= 1 + (0.5 ± 2.1) ×10
−12
, (28.9)
which provides a test of CPT invariance of the electron–
positron system.
The theoretical expression for a
e
may be written as
a
e
(th) = a
e
(QED) + a
e
(weak) + a
e
(had), (28.10)
where the terms denoted by QED, weak, and had account
for the purely quantum electrodynamic, predominantly
electroweak, and predominantly hadronic (that is, strong
interaction) contributions to a
e
, respectively. The QED
contribution may be written as [28.5]
a
e
(QED) = A
1
+ A
2
(m
e
/m
µ
) + A
2
(m
e
/m
τ
)
+ A
3
(m
e
/m
µ
, m
e
/m
τ
). (28.11)
The term A
1
is mass independent and the other terms
are functions of the indicated mass ratios. For these
terms the lepton in the numerator of the mass ratio is
the particle under consideration, while the lepton in the
denominator of the ratio is the virtual particle that is the
source of the vacuum polarization that gives rise to the
term.
Each of the four terms on the right-hand side of
(28.11) is expressed as a power series in the fine-
structure constant α:
A
i
= A
(2)
i
α
π
+ A
(4)
i
α
π
2
+ A
(6)
i
α
π
3
+ A
(8)
i
α
π
4
+··· . (28.12)
The fine-structure constant α is proportional to the
square of the elementary charge e, and the order of a term
containing (α/π)
n
is 2n and its coefficient is called the
2nth-order coefficient.
The second-order coefficient is known exactly, and
the fourth- and sixth-order coefficients are known ana-
lytically in terms of readily evaluated functions:
A
(2)
1
=
1
2
(28.13)
A
(4)
1
=−0.328 478 965 579 ... (28.14)
A
(6)
1
= 1.181 241 456 ... . (28.15)
A total of 891 Feynman diagrams give rise to the
eighth-order coefficient A
(8)
1
, and only a few of these
are known analytically. However, in an effort begun
in the 1970s, Kinoshita and collaborators have cal-
culated A
(8)
1
numerically (for a summary of some of
this work see [28.6, 7]). The value of A
(8)
1
used in
the 1998 CODATA adjustment of the fundamental con-
stants was − 1.5098 (384) [28.1]. Recently an error in
the program employed in the evaluation of a gauge-
invariant 18 diagram subset of the 891 diagrams was
discovered in the course of carrying out an independent
calculation to check this value [28.8]. The corrected pro-
gram together with improved precision in the numerical
integration for all diagrams leads to the tentative value
A
(8)
1
=−1.7366 (60) [28.9], where the shift from the
earlier value is predominately due to the correction of
the error. As a result of this recent work, Kinoshita and
Nio [28.8] report that the integrals from all 891 Feyn-
man diagrams have now been verified by independent
calculation and/or checked by analytic comparison with
lower-order integrals. Nevertheless, because the preci-
sion of the numerical evaluation of some integrals is still
being improved and a closer examination is being made
Part B 28.1

Tests of Fundamental Physics 28.1 Electron g-Factor Anomaly 431
of the uncertainty of the numerical evaluation of other
integrals, we retain the uncertainty estimate of the earlier
reported value of A
(8)
1
.Thisgives
A
(8)
1
=−1.7366 (384). (28.16)
The 0.0384 standard uncertainty of A
(8)
1
contributes
a standard uncertainty to a
e
(th) of 0.96× 10
−9
a
e
,which
may be compared to the 3.7×10
−9
a
e
uncertainty of the
experimental value (28.8). We also note that work is in
progress on analytic calculations of eighth-order inte-
grals. See, for example, Laporta [28.10]andMastrolia
and Remiddi [28.11].
Little is known about the tenth-order coeffi-
cient A
(10)
1
and higher-order coefficients. To evaluate
the contribution to the uncertainty of a
e
(th) due to
lack of knowledge of A
(10)
1
, we follow [28.1] to obtain
A
(10)
1
= 0.0(3.8). Because the 3.8 standard uncertainty
of A
(10)
1
contributes a standard uncertainty component
to a
e
(th) of only 0.22 × 10
−9
a
e
, the uncertainty contri-
butions to a
e
(th) from all other higher-order coefficients
are assumed to be negligible.
The mass-dependent coefficients of possible inter-
est and corresponding contributions to a
e
(th), based on
the 2002 CODATA recommended values of the mass
ratios [28.3], are
A
(4)
2
(m
e
/m
µ
) = 5.197 386 70 (27) ×10
−7
→ 2.418 × 10
−9
a
e
, (28.17)
A
(4)
2
(m
e
/m
τ
) = 1.837 63 (60) ×10
−9
→ 0.009 × 10
−9
a
e
, (28.18)
A
(6)
2
(m
e
/m
µ
) =−7.373 941 58 (28) ×10
−6
→−0.080 × 10
−9
a
e
, (28.19)
A
(6)
2
(m
e
/m
τ
) =−6.5819 (19) ×10
−8
→−0.001 × 10
−9
a
e
, (28.20)
where the standard uncertainties of the coefficients are
due to the uncertainties of the mass ratios. However,
the contributions are so small that the uncertainties of
the mass ratios are negligible. It may also be noted
that the contributions from A
(6)
3
(m
e
/m
µ
, m
e
/m
τ
) and
all higher-order mass-dependent terms are negligible as
well.
For the electroweak contribution we have
a
e
(weak) = 0.0297 (5) ×10
−12
= 0.0256 (5) ×10
−9
a
e
, (28.21)
as in [28.1].
The hadronic contribution is
a
e
(had) = 1.671 (19) ×10
−12
= 1.441 (17) ×10
−9
a
e
, (28.22)
and is the sum of the following three contributions:
a
(4)
e
(had) = 1.875 (18) ×10
−12
obtained by Davier and
Höcker [28.12]; a
(6a)
e
(had) =−0.225 (5) ×10
−12
given
by Krause [28.13]; and a
(γγ)
e
(had) = 0.0210 (36) ×10
−12
obtained by multiplying the corresponding result for the
muon given in [28.3] by the factor (m
e
/m
µ
)
2
,since
a
(γγ)
e
(had) is assumed to vary approximately as m
2
µ
.The
contribution a
e
(had), although larger than a
e
(weak),is
not yet of major significance.
Since the dependence on α of any contribution other
than a
e
(QED) is negligible, we obtain a convenient form
for the function by combining terms in a
e
(QED) that
have like powers of α/π. This leads to the following
summary of the above results:
a
e
(th) = a
e
(QED) + a
e
(weak) + a
e
(had), (28.23)
where
a
e
(QED) = C
(2)
e
α
π
+ C
(4)
e
α
π
2
+ C
(6)
e
α
π
3
+ C
(8)
e
α
π
4
+ C
(10)
e
α
π
5
+··· ,
(28.24)
with
C
(2)
e
= 0.5 ,
C
(4)
e
=−0.328 478 444 00 ,
C
(6)
e
= 1.181 234 017 ,
C
(8)
e
=−1.7366 (384),
C
(10)
e
= 0.0 (3.8), (28.25)
and where
a
e
(weak) = 0.030 (1) ×10
−12
(28.26)
and
a
e
(had) = 1.671 (19) ×10
−12
. (28.27)
The standard uncertainty of a
e
(th) from the uncertainties
of the terms listed above, other than that due to α,is
u[a
e
(th)]=1.15 × 10
−12
= 0.99 × 10
−9
a
e
, (28.28)
and is dominated by the uncertainty of the coeffi-
cient C
(8)
e
.
We define an additive correction δ
e
to a
e
(th) to ac-
count for the lack of exact knowledge of a
e
(th), and
Part B 28.1

432 Part B Atoms
hence the complete theoretical expression for the elec-
tron anomaly is
a
e
(α, δ
e
) = a
e
(th) + δ
e
, (28.29)
where all the uncertainty is associated with δ
e
.Thethe-
oretical estimate of δ
e
is zero and its standard uncertainty
is u[a
e
(th)]:
δ
e
= 0.0 (1.1) ×10
−12
. (28.30)
Equating the theoretical expression with a
e
(exp)
given in (28.8) yields
α
−1
(a
e
) = 137.035 998 80 (52). (28.31)
The uncertainty of a
e
(th) is significantly smaller than
the uncertainty of a
e
(exp), and thus the uncertainty
of this inferred value of α is determined mainly by
the uncertainty of a
e
(exp). This result has the smallest
uncertainty of any value of alpha currently avail-
able.
This result compares favorably with the value
α
−1
(recoil) = 137.036 0001 (11) (28.32)
derived from the atomic recoil frequency shift of pho-
tons absorbed and emitted by cesium, as reviewed
in [28.3].
28.2 Electron g-Factor in
12
C
5+
and
16
O
7+
For a ground-state hydrogenic ion
A
X
(Z−1)+
with
mass number A, atomic number (proton number) Z,
nuclear spin quantum number i = 0, and g-factor
g
e
−
A
X
(Z−1)+
in an applied magnetic flux density B,
the ratio of the electron’s spin-flip (often called pre-
cession) frequency f
s
=
g
e
−
A
X
(Z−1)+
(e
/2m
e
)B/h
to the cyclotron frequency of the ion f
c
= (Z − 1)
eB/2πm(
A
X
(Z−1)+
) in the same magnetic flux density
is
f
s
A
X
(Z−1)+
f
c
A
X
(Z−1)+
=−
g
e
−
A
X
(Z−1)+
2(Z − 1)
A
r
A
X
(Z−1)+
A
r
(e)
,
(28.33)
where A
r
(X) is the relative atomic mass of particle X.
If the frequency ratio f
s
/ f
c
is determined experimen-
tally with high accuracy, and A
r
A
X
(Z−1)+
of the ion
is also accurately known, then this expression can be
used to determine an accurate value of A
r
(e), assuming
the bound-state electron g-factor can be calculated from
QED theory with sufficient accuracy; or the g-factor can
be determined if A
r
(e) is accurately known from another
experiment. In fact, a broad program involving workers
from a number of European laboratories has been under-
way since about the mid-1990s to measure the frequency
ratio and calculate the g-factor for different ions, most
notably (to date)
12
C
5+
and
16
O
7+
. The measurements
themselves are being performed at the GSI (Gesellschaft
für Schwerionenforschung, Darmstadt, Germany) by
GSI and University of Mainz researchers. Values re-
ported are [28.14–16]
f
s
12
C
5+
f
c
12
C
5+
= 4376.210 4989 (23)
(28.34)
and [28.16–18]
f
s
16
O
7+
f
c
16
O
7+
= 4164.376 1836 (31).
(28.35)
It should be noted that these two frequency ratios are
correlated. Based on the detailed uncertainty budget of
the two results [28.16], we find
r
f
s
12
C
5+
f
c
12
C
5+
,
f
s
16
O
7+
f
c
16
O
7+
= 0.035
(28.36)
for the correlation coefficient.
We next consider the g-factor in (28.33) for an elec-
tron in the 1S state of hydrogen-like carbon 12 (atomic
number Z = 6, nuclear spin quantum number i = 0) or in
the 1S state of hydrogen-like oxygen 16 (atomic number
Z = 8, nuclear spin quantum number i = 0) within the
framework of relativistic bound-state theory. The meas-
ured quantity is the transition frequency between the
two Zeeman levels of the atom in an externally applied
magnetic field.
The energy of a free electron with spin projection s
z
in a magnetic flux density B in the z direction is
E
s
z
=−g
e
−
e
2m
e
s
z
B , (28.37)
and hence the spin-flip energy difference is
∆E =−g
e
−
µ
B
B . (28.38)
(In keeping with the definition of the g-factor in
Sect. 28.1 the quantity g
e
−
is negative.) The analogous
expressions for the ions considered here are
∆E
b
(X) =−g
e
−
(X)µ
B
B , (28.39)
Part B 28.2
Tests of Fundamental Physics 28.2 Electron g-Factor in
12
C
5+
and
16
O
7+
433
which defines the bound-state electron g-factor in the
case where there is no nuclear spin, and where X is
either
12
C
5+
or
16
O
7+
.
The main theoretical contributions to g
e
−
(X) can be
categorized as follows:
•
Dirac (relativistic) value g
D
;
•
radiative corrections ∆g
rad
;
•
recoil corrections ∆g
rec
;
•
nuclear size corrections ∆g
ns
.
Thus we write
g
e
−
(X) = g
D
+ ∆g
rad
+ ∆g
rec
+ ∆g
ns
+··· ,
(28.40)
where terms accounting for other effects are assumed
to be negligible at the current level of uncertainty of
the relevant experiments (relative standard uncertainty
u
r
≈ 6×10
−10
). These theoretical contributions are dis-
cussed in the following paragraphs; numerical results
are summarized in Tables 28.1, 28.2.
Breit [28.19] obtained the exact value
g
D
=−
2
3
1 + 2
1 − (Zα)
2
=−2
1 −
1
3
(Zα)
2
−
1
12
(Zα)
4
−
1
24
(Zα)
6
+···
(28.41)
from the Dirac equation for an electron in the field of
a fixed point charge of magnitude Ze, where the only
uncertainty is that due to the uncertainty in α.
The radiative corrections may be written as
∆g
rad
=−2
C
(2)
e
(Zα)
α
π
+ C
(4)
e
(Zα)
α
π
2
+···
, (28.42)
where the coefficients C
(2n)
e
(Zα), corresponding to n vir-
tual photons, are slowly varying functions of Zα.These
coefficients are defined in direct analogy with the cor-
responding coefficients for the free electron C
(2n)
e
given
in Sect. 28.1 so that
lim
Zα→0
C
(2n)
e
(Zα) = C
(2n)
e
. (28.43)
The coefficient C
(2)
e
(Zα) has been calculated to second
order in Zα by Grotch [28.20] who finds
C
(2)
e
(Zα) = C
(2)
e
+
1
12
(Zα)
2
+···
=
1
2
+
1
12
(Zα)
2
+··· . (28.44)
This result has been confirmed by Faustov and
Close [28.21]andOsborn [28.22], as well as by others.
The terms listed in (28.44) do not provide a value of
C
(2)
e
(Zα) which is sufficiently accurate at the level of un-
certainty of the current experimental results. However,
Yerokh in [28.23, 24] have recently calculated numer-
ically the self-energy contribution C
(2)
e,SE
(Zα) to the
coefficient to all orders in Zα over a wide range of Z.
These results are in general agreement with, but are more
accurate than, the earlier results of Beier et al. [28.25]
and Beier [28.26]. Other calculations of the self en-
ergy have been carried out by Persson [28.27]; Blundell
et al. [28.28]; and Goidenko [28.29]. For Z = 6and
Z = 8 the calculation of Yero khin et al. [28.23]gives
C
(2)
e,SE
(6α) = 0.500 183 609 (19)
C
(2)
e,SE
(8α) = 0.500 349 291 (19), (28.45)
where we have converted their quoted result to conform
with our notation convention, taking into account the
value of α employed in their calculation.
Table 28.1 Theoretical contributions and total for the
g-factor of the electron in hydrogenic carbon 12 based on
the 2002 recommended values of the constants
Contribution Value Source (Eq.)
Dirac g
D
−1.998 721 354 39 (1) (28.41)
∆g
(2)
SE
−0.002 323 672 45 (9) (28.45)
∆g
(2)
VP
0.000 000 008 51 (28.49)
∆g
(4)
0.000 003 545 74 (16) (28.53)
∆g
(6)
−0.000 000 029 62 (28.54)
∆g
(8)
0.000 000 000 10 (28.55)
∆g
rec
−0.000 000 087 64 (1) (28.56, 28.58)
∆g
ns
−0.000 000 000 41 (28.60)
g
e
−
(
12
C
5+
) −2.001 041 590 16 (18) (28.61)
Table 28.2 Theoretical contributions and total for the
g-factor of the electron in hydrogenic oxygen 16 based
on the 2002 recommended values of the constants
Contribution Value Source (Eq.)
Dirac g
D
−1.997 726 003 06 (2) (28.41)
∆g
(2)
SE
−0.002 324 442 15 (9) (28.45)
∆g
(2)
VP
0.000 000 026 38 (28.49)
∆g
(4)
0.000 003 546 62 (42) (28.53)
∆g
(6)
−0.000 000 029 62 (28.54)
∆g
(8)
0.000 000 000 10 (28.55)
∆g
rec
−0.000 000 117 02 (1) (28.56, 28.58)
∆g
ns
−0.000 000 001 56 (1) (28.60)
g
e
−
(
16
O
7+
) −2.000 047 020 31 (43) (28.61)
Part B 28.2
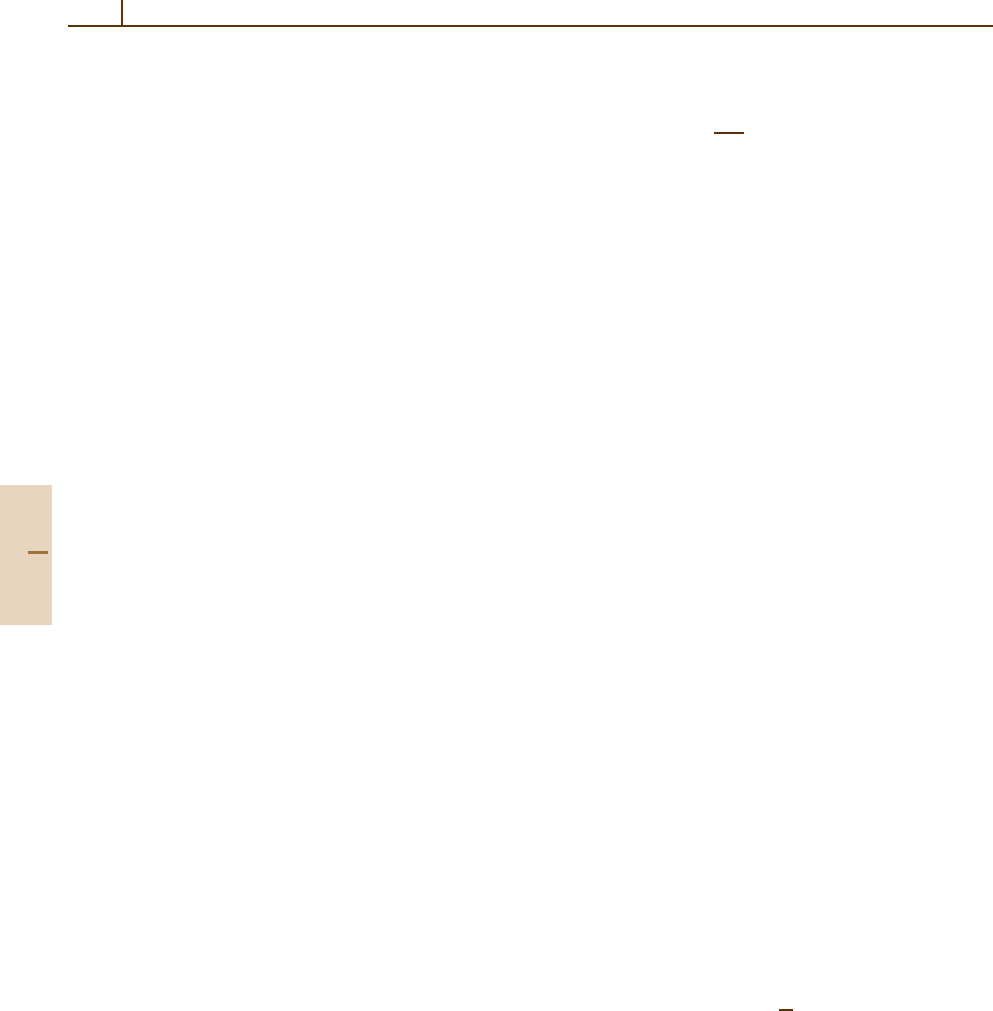
434 Part B Atoms
The lowest-order vacuum-polarization correction is
conveniently considered as consisting of two parts. In
one the vacuum polarization loop modifies the inter-
action between the bound electron and the Coulomb
field of the nucleus, and in the other the loop modifies
the interaction between the bound electron and the ex-
ternal magnetic field. The first part, sometimes called
the “wave function” correction, has been calculated nu-
merically by Beier et al. [28.25], with the result (in our
notation)
C
(2)
e,VPwf
(6α) =−0.000 001 840 3431 (43),
C
(2)
e,VPwf
(8α) =−0.000 005 712 028 (26). (28.46)
Each of these values is the sum of the Uehling poten-
tial contribution and the higher-order Wichmann–Kroll
contribution, which were calculated separately.
The values in (28.46) are consistent with the re-
sult of an evaluation of the correction in powers of
Zα. Terms to order (α/π)(Zα)
7
have been calculated
for the Uehling potential contribution [28.30–32]; and
an estimate of the leading order (α/π)(Zα)
6
term of
the Wichmann–Kroll contribution has been given by
Karshenboim et al. [28.32] based on a prescription of
Karshenboim [28.30]. To the level of uncertainty of in-
terest here, the values from the power series are the
same as the numerical values in (28.46). (Note that for
the Wichmann–Kroll term, the agreement between the
power-series results and the numerical results is im-
proved by an order of magnitude if an additional term
in the power series for the energy level [28.33]usedin
Karshenboim’s prescription is included.)
For the second part of the lowest-order vacuum po-
larization correction, sometimes called the “potential”
correction, Beier et al. [28.25] found that the Uehling
potential contribution is zero. They also calculated the
Wichmann–Kroll contribution numerically over a wide
range of Z. Their value at low Z is very small and
only an uncertainty estimate of 3 × 10
−10
in g is given
because of poor convergence of the partial wave expan-
sion. The reduction in uncertainty (by a factor of 30
for carbon) employed by Beier et al. [28.14] for this
term, based on the assumption that it is of the order of
(α/π)(Zα)
7
, is not considered here, because the refer-
ence quoted for this estimate [28.32] does not explicitly
discuss this term. Yerokh in et al. [28.23] obtained numer-
ical values for this contribution for carbon and oxygen
by a least-squares fit to the values of Beier et al. [28.25]
at higher Z.
Subsequently, Karshenboim and Milstein [28.34]an-
alytically calculated the Wichmann–Kroll contribution
to the potential correction to lowest order in Zα.Their
result in our notation is
C
(2)
e,VPp
(Zα) =
7π
432
(Zα)
5
+··· . (28.47)
This result, together with the numerical values from
Beier [28.26], yields
C
(2)
e,VPp
(6α) = 0.000 000 007 9595 (69),
C
(2)
e,VPp
(8α) = 0.000 000 033 235 (29), (28.48)
which are used in the present analysis. We ob-
tained these results by fitting a function of the
form
a + bZα + c(Zα)
2
(Zα)
5
to the point in (28.47)
and two values of the complete function calculated
by [28.26] (separated by about 10 calculated values)
and evaluating the fitted function at Z = 6or8.This
was done for a range of pairs of points from [28.26], and
the results in (28.48) are the apparent limit of the val-
uesasthelowerZ member of the pair used in the fit
approaches either 6 or 8 as appropriate. (This general
approach is described in more detail in [28.35].)
The total one-photon vacuum polarization coeffi-
cients are given by the sum of (28.46)and(28.48):
C
(2)
e,VP
(6α) = C
(2)
e,VPwf
(6α) + C
(2)
e,VPp
(6α)
=−0.000 001 832 384 (11) ;
C
(2)
e,VP
(8α) = C
(2)
e,VPwf
(8α) + C
(2)
e,VPp
(8α)
=−0.000 005 678 793 (55).
(28.49)
The total for the one-photon coefficient C
(2)
e
(Zα),given
by the sum of (28.45)and(28.49), is
C
(2)
e
(6α) = C
(2)
e,SE
(6α) + C
(2)
e,VP
(6α)
= 0.500 181 777 (19),
C
(2)
e
(8α) = C
(2)
e,SE
(8α) + C
(2)
e,VP
(8α)
= 0.500 343 613 (19),
(28.50)
where in this case, following Beier et al. [28.25], the
uncertainty is simply the sum of the individual uncer-
tainties in (28.45)and(28.49). The total one-photon
contribution ∆g
(2)
to the g-factor is thus
∆g
(2)
=−2C
(2)
e
(Zα)
α
π
=−0.002 323 663 93 (9) for Z = 6
=−0.002 324 415 77 (9) for Z = 8 .
(28.51)
The separate one-photon self energy and vacuum po-
larization contributions to the g-factor are given in
Tables 28.1, 28.2.
Part B 28.2
Tests of Fundamental Physics 28.2 Electron g-Factor in
12
C
5+
and
16
O
7+
435
Evaluations by Eides and Grotch [28.36]usingthe
Bargmann–Michel–Telegdi equation and by Czarnecki
et al. [28.37] using an effective potential approach yield
C
(2n)
e
(Zα) = C
(2n)
e
1 +
(Zα)
2
6
+···
(28.52)
as the leading binding correction to the free electron
coefficients C
(2n)
e
for any n.Forn = 1, this result was
already known, as is evident from (28.44). We include
this correction for the two-photon term, that is, for n = 2,
which gives
C
(4)
e
(Zα) = C
(4)
e
1 +
(Zα)
2
6
+···
=−0.328 583 (14) for Z = 6
=−0.328 665 (39) for Z = 8 ,
(28.53)
here C
(4)
e
=−0.328 478 444 ... . The uncertainty is due
to uncalculated terms and is obtained by assuming that
the unknown higher-order terms for n = 2, represented
by the dots in (28.52), are the same as the higher-order
terms for n = 1 as can be deduced by comparing the
numerical results given in (28.50)to(28.44). This is
the same general approach as that employed by Beier
et al. [28.14].
The three-photon term is calculated in a similar way
but the uncertainty due to uncalculated higher-order
terms is negligible:
C
(6)
e
(Zα) = C
(6)
e
1 +
(Zα)
2
6
+···
= 1.1816 ... for Z = 6
= 1.1819 ... for Z = 8 ,
(28.54)
where C
(6)
e
= 1.181 234 ... . For the four-photon cor-
rection, at the level of uncertainty of current interest,
only the free-electron coefficient is necessary:
C
(8)
e
(Zα) ≈ C
(8)
e
=−1.7366 (384). (28.55)
The preceding corrections ∆g
D
and ∆g
rad
are based
on the approximation that the nucleus of the hydrogenic
atom has an infinite mass. The recoil correction to the
bound-state g-factor associated with the finite mass of
the nucleus is denoted by ∆g
rec
, which we write here as
the sum ∆g
(0)
rec
+ ∆g
(2)
rec
corresponding to terms that are
zero- and first-order in α/π, respectively. For ∆g
(0)
rec
,we
have
∆g
(0)
rec
=
− (Zα)
2
+
(Zα)
4
3
1 +
1 − (Zα)
2
2
− (Zα)
5
P(Zα)
m
e
m
N
+ O
m
e
m
N
2
=−0.000 000 087 71 (1)... for Z = 6
=−0.000 000 117 11 (1)... for Z = 8 ,
(28.56)
where m
N
is the mass of the nucleus. The
mass ratios, obtained from the 2002 CODATA
adjustment, are m
e
/m
12
C
6+
= 0.000 045 7275 ...
and m
e
/m
16
O
8+
= 0.000 034 3065 ....In(28.56),
the first term in the brackets was calculated by
Grotch [28.38]. Shortly thereafter, this term and
higher-order terms were obtained by Grotch [28.39],
Hegstrom [28.40], Faustov [28.21], Close and Os-
born [28.22], and Grotch and Hegstrom [28.41](see
also Hegstrom [28.42]andGrotch [28.20]). The sec-
ond and third terms in the brackets were calculated by
Shabaev and Yerok hin [28.43] based on the formula-
tion of Shabaev [28.44](seealsoYelkhovski [28.45]).
Shabaev and Yerokhin have numerically evaluated the
function P(Zα) over a wide range of Z, with the re-
sult P(6α) = 10.493 95 (1) for hydrogenic carbon and
P(8α) = 9.300 18 (1) for hydrogenic oxygen.
An additional term of the order of the mass ratio
squared has been considered by various authors. Earlier
calculations of this term for atoms with a spin one-half
nucleus, such as muonium, have been done by Close and
Osborn [28.22]andGrotch and Hegstrom [28.41](see
also Eides and Grotch [28.36]). Their result for this term
is
(1 + Z)(Zα)
2
m
e
m
N
2
. (28.57)
Eides and Grotch [28.36], Eides [28.46] find that this
correction to the g-factor is independent of the spin of the
nucleus, so (28.57) gives the correction for carbon and
oxygen, as well as atoms with a spin one-half nucleus.
On the other hand, Martynenko and Faustov [28.47,48]
find that the correction of this order depends on the spin
of the nucleus and give a result with the factor 1 + Z
replaced by Z/3 for a spin zero nucleus. In view of
Part B 28.2

436 Part B Atoms
this discrepancy, we include a contribution to ∆g
(0)
rec
in
(28.56) that is the average of the two quoted results with
an uncertainty of half of the difference between them.
For ∆g
(2)
rec
,wehave
∆g
(2)
rec
=
α
π
(Zα)
2
3
m
e
m
N
+···
= 0.000 000 000 06 ... for Z = 6
= 0.000 000 000 09 ... for Z = 8 ,
(28.58)
There is a small correction to the bound-state
g-factor due to the finite size of the nucleus:
∆g
ns
=
8
3
(Zα)
4
R
N
λ
C
2
+··· , (28.59)
where R
N
is the bound-state nuclear rms charge ra-
dius and
λ
C
is the Compton wavelength of the electron
divided by 2π.In(28.59), the term shown is the nonrela-
tivistic approximation given by Karshenboim [28.30].
This term and the dominant relativistic correction have
been calculated by Glazov and Shabaev [28.49]. We
take R
N
= 2.4705 (23) fm and R
N
= 2.6995 (68) from
the compilation of Angeli [28.50] for the values of the
12
Cand
16
O nuclear radii, respectively, which, based on
Glazov and Shabaev [28.49], yields
∆g
ns
=−0.000 000 000 41 for
12
C ,
∆g
ns
=−0.000 000 001 56 (1) for
16
O . (28.60)
The theoretical value for the g-factor of the electron
in hydrogenic carbon 12 or oxygen 16 is the sum of the
individual contributions discussed above and summar-
ized in Tables 28.1 and 28.2:
g
e
−
12
C
5+
=−2.001 041 590 16 (18)
g
e
−
16
O
7+
=−2.000 047 020 31 (43).
(28.61)
We define g
C
(th) to be the sum of g
D
as given
in (28.41), the term −2(α/π)C
(2)
e
, and the numerical
values of the remaining terms in (28.40)asgivenin
Table 28.1 without the uncertainties. The standard un-
certainty of g
C
(th) from the uncertainties of these latter
terms is
u[g
C
(th)]=1.8×10
−10
= 9.0×10
−11
|g
C
(th)| .
(28.62)
The uncertainty in g
C
(th) due to the uncertainty in α en-
ters primarily through the functional dependence of g
D
and the term −2(α/π)C
(2)
e
on α. Therefore this particu-
lar component of uncertainty is not explicitly included in
u[g
C
(th)], but it is included in Tables 28.1 and 28.2.To
take the uncertainty u[g
C
(th)] into account we employ
as the theoretical expression for the g-factor
g
C
(α, δ
C
) = g
C
(th) + δ
C
, (28.63)
where the input value of the additive correction δ
C
is
taken to be zero and its standard uncertainty is u[g
C
(th)]:
δ
C
= 0.0 (1.8) ×10
−10
. (28.64)
Analogous considerations apply for the g-factor in oxy-
gen:
u[g
O
(th)]=4.3×10
−10
= 2.2×10
−10
|g
O
(th)|
(28.65)
g
O
(α, δ
O
) = g
O
(th) + δ
O
(28.66)
δ
O
= 0.0 (4.3) ×10
−10
. (28.67)
Since the uncertainties of the theoretical values of
the carbon and oxygen g-factors arise primarily from
the same sources, the quantities δ
C
and δ
O
are highly
correlated. Their covariance is
u(δ
C
,δ
O
) = 741 × 10
−22
, (28.68)
which corresponds to a correlation coefficient of
r(δ
C
,δ
O
) = 0.95.
The theoretical value of the ratio of the two g-factors,
which is relevant to the following discussion, is
g
e
−
12
C
5+
g
e
−
16
O
7+
= 1.000 497 273 23 (13),
(28.69)
where the covariance is taken into account in calculat-
ing the uncertainty, and for this purpose includes the
contribution due to the uncertainty in α.
Finally, we consider evaluation of the mass ratio
in (28.33) by applying the relation for the relative atomic
mass A
r
A
X
of a neutral atom
A
X in terms of the
relative atomic mass of an ion of the atom formed by the
removal of n electrons, which is given by
A
r
A
X
= A
r
A
X
n+
+ nA
r
(e)
−
E
b
A
X
− E
b
A
X
n+
m
u
c
2
. (28.70)
Here A is the mass number, Z is the atomic number (pro-
ton number), E
b
A
X
/m
u
c
2
is the relative-atomic-mass
equivalent of the total binding energy of the Z electrons
of the atom, E
b
A
X
n+
/m
u
c
2
is the relative-atomic-
mass-equivalent of the binding energy of the
A
X
n+
ion,
and m
u
is the atomic mass constant.
Part B 28.2
Tests of Fundamental Physics 28.3 Hydrogen and Deuterium Atoms 437
From (28.33)and(28.70), we have
f
s
12
C
5+
f
c
12
C
5+
=−
g
e
−
12
C
5+
10A
r
(e)
×
12 − 5 A
r
(e) +
E
b
12
C
− E
b
12
C
5+
m
u
c
2
,
(28.71)
which is the equation for the
12
C
5+
frequency-ratio.
Evaluation of this expression using the result for
f
s
12
C
5+
/f
c
12
C
5+
in (28.34), the theoretical result
for g
e
−
12
C
5+
in Table 28.1, and the relevant bind-
ing energies from [28.3], yields
A
r
(e) = 0.000 548 579 909 31 (29), (28.72)
a result that is consistent with the University of Washing-
ton result [28.51], but has about a factor of four smaller
uncertainty.
Similarly, we have
f
s
16
O
7+
f
c
16
O
7+
=−
g
e
−
16
O
7+
14A
r
(e)
A
r
16
O
7+
(28.73)
with
A
r
16
O
= A
r
16
O
7+
+ 7A
r
(e)
−
E
b
16
O
− E
b
16
O
7+
m
u
c
2
, (28.74)
which are the equations for the oxygen frequency ra-
tio and A
r
16
O
, respectively. The first expression,
evaluated using the result for f
s
16
O
7+
/ f
c
16
O
7+
in
(28.35) and the theoretical result for g
e
−
16
O
7+
in Ta-
ble 28.2, in combination with the second expression,
evaluated using the value of A
r
16
O
from the Univer-
sity of Washington group [28.52, 53] and the relevant
binding energies from [28.3], yields
A
r
(e) = 0.000 548 579 909 57 (43), (28.75)
a value that is consistent with both the University of
Washington value [28.51] and the value in (28.72) ob-
tained from f
s
12
C
5+
/ f
c
12
C
5+
.
As a consistency test, it is of interest to com-
pare the experimental and theoretical values of the
ratio of g
e
−
12
C
5+
to g
e
−
16
O
7+
[28.54]. The main
reason is that the experimental value of the ratio is
only weakly dependent on the value of A
r
(e).The
theoretical value of the ratio is given in (28.69)and
takes into account the covariance of the two the-
oretical values. The experimental value of the ratio
can be obtained by combining (28.34)to(28.36),
(28.71), (28.73), and (28.74), and using the 2002
CODATA recommended value for A
r
(e). (Because of
the weak dependence of the experimental ratio on
A
r
(e), the value used is not at all critical.) The result
is
g
e
−
12
C
5+
g
e
−
16
O
7+
= 1.000 497 273 70 (90),
(28.76)
in agreement with the theoretical value in (28.69).
28.3 Hydrogen and Deuterium Atoms
This section gives a brief survey of the theory of the
energy levels of hydrogen and deuterium relevant to
measurements of transition frequencies. Although in-
formation to completely determine the theoretical values
for the energy levels is provided, results that are included
in [28.1, 2] are given with minimal discussion, and the
emphasis is on recent results. For brevity, reference to
most historical works is not included.
The theoretical data provided here are confined to
that needed to evaluate the theoretical values of the pre-
cisely measured transition frequencies in hydrogen and
deuterium summarized in [28.3].
It should be noted that the theoretical values of the
energy levels of different states of hydrogen and deu-
terium are highly correlated. For example, for S states,
the uncalculated terms are primarily of the form of
an unknown common constant divided by n
3
.This
fact is taken into account by calculating covariances
between energy levels in addition to the uncertain-
ties of the individual levels as discussed in detail in
Sect. 28.3.12. To provide the information needed to cal-
culate the covariances, where necessary we distinguish
between components of uncertainty that are proportional
to 1/n
3
, denoted by u
0
, and components of uncer-
tainty that are essentially random functions of n, denoted
by u
n
.
Theoretical values of the energy levels of hydro-
gen and deuterium atoms are determined mainly by
the Dirac eigenvalue, QED effects such as self energy
and vacuum polarization, and nuclear size and mo-
tion effects. We consider each of these contributions
in turn.
Part B 28.3
438 Part B Atoms
28.3.1 Dirac Eigenvalue
The binding energy of an electron in a static Coulomb
field (the external electric field of a point nucleus of
charge Ze with infinite mass) is determined predomin-
antly by the Dirac eigenvalue
E
D
=
1 +
(Zα)
2
(n − δ)
2
−1/2
m
e
c
2
, (28.77)
where n is the principal quantum number,
δ =|κ|−
κ
2
− (Zα)
2
1/2
, (28.78)
and κ is the angular momentum-parity quantum number
(κ =−1, 1, −2, 2, −3forS
1/2
,P
1/2
,P
3/2
,D
3/2
,and
D
5/2
states, respectively). States with the same principal
quantum number n and angular momentum quantum
number j =|κ|−
1
2
have degenerate eigenvalues. The
nonrelativistic orbital angular momentum is given by
l =
κ +
1
2
−
1
2
. (Although we are interested only in the
case where the nuclear charge is e, we retain the atomic
number Z in order to indicate the nature of various
terms.)
Corrections to the Dirac eigenvalue that approxi-
mately take into account the finite mass of the nucleus
m
N
are included in the more general expression for
atomic energy levels, which replaces (28.77) [28.55,56]:
E
M
= Mc
2
+[f(n, j ) − 1]m
r
c
2
−[f(n, j ) − 1]
2
m
2
r
c
2
2M
+
1 − δ
l0
κ(2l + 1)
(Zα)
4
m
3
r
c
2
2n
3
m
2
N
+··· , (28.79)
where
f(n, j ) =
1 +
(Zα)
2
(n − δ)
2
−1/2
, (28.80)
M = m
e
+ m
N
,andm
r
= m
e
m
N
/(m
e
+ m
N
) is the re-
duced mass.
28.3.2 Relativistic Recoil
Relativistic corrections to (28.79) associated with mo-
tion of the nucleus are considered relativistic-recoil
corrections. The leading term, to lowest order in Zα
and all orders in m
e
/m
N
, is [28.56, 57]
E
S
=
m
3
r
m
2
e
m
N
(Zα)
5
πn
3
m
e
c
2
×
1
3
δ
l0
ln(Zα)
−2
−
8
3
ln k
0
(n, l) −
1
9
δ
l0
−
7
3
a
n
−
2
m
2
N
− m
2
e
δ
l0
m
2
N
ln
m
e
m
r
− m
2
e
ln
m
N
m
r
,
(28.81)
where
a
n
=−2
ln
2
n
+
n
i=1
1
i
+ 1 −
1
2n
δ
l0
+
1 − δ
l0
l(l + 1)(2l + 1)
.
(28.82)
To lowest order in the mass ratio, higher-order cor-
rections in Zα have been extensively investigated; the
contribution of the next two orders in Zα can be written
as
E
R
=
m
e
m
N
(Zα)
6
n
3
m
e
c
2
×
D
60
+ D
72
Zα ln
2
(Zα)
−2
+···
,
(28.83)
where for nS
1/2
states [28.58, 59]
D
60
= 4ln2−
7
2
(28.84)
and for states with l ≥ 1 [28.60–62]
D
60
=
3 −
l(l + 1)
n
2
2
(4l
2
− 1)(2l + 3)
.
(28.85)
(As usual, the first subscript on the coefficient refers to
the power of Zα and the second subscript to the power
of ln(Zα)
−2
.) The next coefficient in (28.83) has been
calculated recently with the result [28.63, 64]
D
72
=−
11
60π
δ
l0
. (28.86)
The relativistic recoil correction used here is based on
(28.81)to(28.86). Numerical values for the complete
contribution of (28.83) to all orders in Zα have been ob-
tained by Shabaev et al. [28.65]. While these results are
in general agreement with the values given by the power
series expressions, the difference between them for
S states is about three times larger than expected (based
on the uncertainty quoted by Shabaev et al. [28.65]and
the estimated uncertainty of the truncated power series
Part B 28.3
Tests of Fundamental Physics 28.3 Hydrogen and Deuterium Atoms 439
which is taken to be one-half the contribution of the term
proportional to D
72
, as suggested by Eides et al. [28.2]).
This difference is not critical, and we allow for the am-
biguity by assigning an uncertainty for S states of 10%
of the contribution given by (28.83). This is sufficiently
large that the power series value is consistent with the
numerical all-order calculated value. For the states with
l ≥ 1, we assign an uncertainty of 1% of the contribu-
tionin(28.83). The covariances of the theoretical values
are calculated by assuming that the uncertainties are
predominately due to uncalculated terms proportional
to (m
e
/m
N
)/n
3
.
28.3.3 Nuclear Polarization
Another effect involving specific properties of the
nucleus, in addition to relativistic recoil, is nuclear polar-
ization. It arises from interactions between the electron
and nucleus in which the nucleus is excited from the
ground state to virtual higher states.
For hydrogen, the result that we use for the nuclear
polarization is [28.66]
E
P
(H) =−0.070 (13)h
δ
l0
n
3
kHz . (28.87)
Larger values for this correction have been reported by
Roedenfelder [28.67], Martynenko and Faustov [28.68],
but apparently they are based on an incorrect formulation
of the dispersion relations [28.2,66].
For deuterium, to a good approximation, the po-
larizability of the nucleus is the sum of the proton
polarizability, the neutron polarizability [28.69], and the
dominant nuclear structure polarizability [28.70], with
the total given by
E
P
(D) =−21.37 (8)h
δ
l0
n
3
kHz . (28.88)
We assume that this effect is negligible in states of
higher l.
28.3.4 Self Energy
The second order (in e, first order in α) level shift due
to the one-photon electron self energy, the lowest-order
radiative correction, is given by
E
(2)
SE
=
α
π
(Zα)
4
n
3
F(Zα)m
e
c
2
, (28.89)
where
F(Zα) = A
41
ln(Zα)
−2
+ A
40
+ A
50
(Zα)
+ A
62
(Zα)
2
ln
2
(Zα)
−2
+ A
61
(Zα)
2
ln(Zα)
−2
+ G
SE
(Zα)(Zα)
2
, (28.90)
with [28.71]
A
41
=
4
3
δ
l0
A
40
=−
4
3
ln k
0
(n, l) +
10
9
δ
l0
−
1
2κ(2l + 1)
(1 − δ
l0
)
A
50
=
139
32
− 2ln2
πδ
l0
A
62
=−δ
l0
A
61
=
4
1 +
1
2
+···+
1
n
+
28
3
ln 2 − 4lnn
−
601
180
−
77
45n
2
δ
l0
+
1 −
1
n
2
2
15
+
1
3
δ
j
1
2
δ
l1
+
96n
2
− 32l(l + 1)
3n
2
(2l − 1)(2l)(2l + 1)(2l + 2)(2l + 3)
× (1 − δ
l0
). (28.91)
Selected Bethe logarithms ln k
0
(n, l) that appear in
(28.91)aregiveninTable28.3 [28.72].
The function G
SE
(Zα) in (28.90) gives the higher-
order contribution (in Zα) to the self energy, and
values for G
SE
(α) are listed in Table 28.4.Forthe
states with n = 1andn = 2, the values in the ta-
ble are based on direct numerical evaluations by
Jentschura et al. [28.73, 74], and the values for the 3S
and 4S states are from Jentschura and Mohr [28.75].
The remaining values of G
SE
(α) are based on the
Table 28.3 Relevant Bethe logarithms ln k
0
(n, l)
n S P D
1 2.984 128 556
2 2.811 769 893 − 0.030 016 709
3 2.767 663 612
4 2.749 811 840 − 0.041 954 895 − 0.006 740 939
6 2.735 664 207 − 0.008 147 204
8 2.730 267 261 − 0.008 785 043
12 − 0.009 342 954
Part B 28.3
