Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


410 Part B Atoms
H the HF Hamiltonian, e
n
≡ e(n) the HF energy,
U
so
v,h
(n) =
3/16π
|0|n|
2
n
1
r
3
n
C
, (26.78)
where
C
=
j = +
1
2
−( +1) j = −
1
2
, (26.79)
ρ(n) =
i/4π
|0|n|
2
a
jk
(e
k
−e
j
)(e
a
−2e
k
+e
j
)
e
a
−e
j
n
a
V
n
j
j|r|k·
k |p|a
+c.c.
,
(26.80)
L
core
(n) =
i/4π
|0|n|
2
a
jk
(e
k
−e
j
)(e
a
−2e
k
+e
j
)
e
a
−e
j
n
a
V
n
j
ln
Z
2
2|e
a
−e
k
|
j|r|k· k|p|a+c.c.
,
(26.81)
U
(1)
(n) =
1/2π
|0|n|
2
a
a
p
2
a
n
a
V
n
a
−
n
(a)
V
n
(a)
−
%
(b)
a
V
a
(b)
+c.c.
&
δ
nb
,
(26.82)
U
(2)
(n) =
i/2π
|0|n|
2
a
k<q
(2e
a
−e
k
−e
q
)
e
q
−e
k
n
q
V
n
k
ln
e
a
−e
q
e
a
−e
k
+2
a|p|q
·
k |p|a
+c.c.
,
(26.83)
U
so
core
(n) =
3/16π
|0|n|
2
aj
δ
a
j
e
a
−e
j
n
a
V
n
j
j
1
r
3
a
C
+c.c.
, (26.84)
K
C
(n) =
1
|0|n|
2
a
n
a
δ
3
(x−y)
n
a
,
(26.85)
K
L
(n) =
7/2
|0|n|
2
|
a
'
n
a
1
4π
∇
2
ln(Z|x−y|) +γ
|x−y|
n
a
(
,
(26.86)
where
U(n) ≡ U
(1)
(n) +U
(2)
(n) , (26.87)
r|(a)
≡
d
dr
r|a ,
(26.88)
and γ is the Euler–Mascheroni constant. As in (26.27),
x refers to the top row and y to the bottom row in the
two-row expression in (26.86).
L(n), which is associated with the valence electron
and the nuclear Coulomb potential, has the form of a hy-
drogenic BL, except that it is calculated with HF wave
functions and energies. L
core
(n) comes from BL terms
associated with core electrons.
The expressions appearing in (26.80), (26.81),
and (26.83) originate from the double commutator
[
p· [p, H]
]
, which is then approximated by using the
commutator [r, H]≈ip. This is not an exact result
because the ee exchange term in the HF potential is
neglected. One thus obtains [26.13]
m
|
[
p· [p, H]
]
|
n
(26.89)
≈ i(e
n
−2e
k
+e
m
)(e
k
−e
n
)
m
|
p
|
k
·
k
|
r
|
n
.
A less accurate approximation is [26.12]
4πZδ
3
(r) ≈
[
p· [p, H]
]
. (26.90)
Using the left-hand side of this equation instead of the
approximation (26.89) to the right-hand side would lead
to only s-state a, j and p-state k contributions in (26.80)
and alternative forms of (26.81)and(26.83).
The major part of the contribution to the energy due
to radiative corrections comes from F
v,h
(n, 0) (s-states),
and numerical tests indicate that the principal effect in
this term comes from the renormalization of the electron
density at the coordinate origin due to electron shielding.
Part B 26.4
Green’s Functions of Field Theory References 411
This reduction occurs because the shielded wave func-
tion is more spread out than the unshielded one. Thus,
one can extend the above results semi-empirically to
high Z (for which F
core
(n,)and F
ee
(n,)play a much
smaller role because of their 1/Z dependence) by using
the hydrogenic results [26.27] for high Z, i. e., replac-
ing Z
4
for hydrogen by Z(Z
n,eff
)
3
for 1P/1H atoms
(where Z
n,eff
is the shielded nuclear charge number,
defined in (26.68), and Z is the unshielded nuclear
charge number). The results obtained in this way are
competitive with other evaluations of ∆E
n
[26.28].
Finally, there is a correction to F(n,)for smaller Z
when the integral equations for the self-energy and
vacuum polarization contributions are solved more accu-
rately than by iteration. These corrections play little role
in s-state energies, but are somewhat more important in
p-states for the hard core case (closed shells, N = 2, 10,
etc.). They are expected to provide a much more signifi-
cant contribution in the soft core case (closed subshells,
N = 4, 12, etc.).
The correction is based on the simpler approximation
given in (26.90) of the more accurate (26.89). It is given
by
δF(n,)=
1
Z0|n
2
a
j
n
a
V
n
j
e
a
−e
j
[
j|E |a
− ZF
(0)
v,h
j|0
0|a
+c.c.
,
(26.91)
where
j|E |a
= ZF
(0)
v,h
j|0
0|a
+
b
k
j
b
V
a
k
e
b
−e
k
[
k |E |b
+c.c.
]
,
(26.92)
F
(o)
v,h
=
4
3
{N(Z) +L} .
(26.93)
The inhomogeneous term in (26.92) appears only
for states |j and |a which are s-states. L in (26.93)is
taken to be a constant, an approximation sufficient for
the desired accuracy, and reflects the fact that L(n, 0)
for s-states is essentially constant as a function of radial
quantum number, and is approximately the same for
hydrogen and the HF approximation.
In order to obtain the correction δF(n,) of
(26.91), it is necessary first to solve the coupled in-
homogeneous linear equations of (26.92). While the
sum
a
over core states is always over a finite
number of discrete states, the symbol
denotes
an infinite sum over discrete bound valence states
and an integral over the continuum of such states.
Indeed, expressions of this type occur throughout
the GFA. They can be dealt with by the use of
finite basis techniques, for example the B-spline ap-
proach [26.29, 30].
References
26.1 A. L. Fetter, J. D. Walecka: Quantum Theory of Many
Particle Systems (McGraw-Hill, New York 1971)
26.2 Gy. 1Csanak, H. S. Taylor, R. Yaris: Adv. Atom. Mol.
Phys. 7, 287 (1971)
26.3 G. Feldman, T. Fulton: Ann. Phys. (N. Y.) 172,40
(1986)
26.4 G. Feldman, T. Fulton: Ann. Phys. (N. Y.) 179,20
(1987)
26.5 W. R. Johnson, S. A. Blundell, J. Sapirstein: Phys.
Rev. A 37, 2764 (1988)
26.6 W. R. Johnson, S. A. Blundell, Z. W. Liu, J. Sapirstein:
Phys. Rev. A 40, 2233 (1989)
26.7 G. Feldman, T. Fulton: Ann. Phys. (N. Y.) 152, 376
(1984)
26.8 S.-S. Liaw, G. Feldman, T. Fulton: Phys. Rev. A 38,
5985 (1988)
26.9 S.-S. Liaw: Phys. Rev. A 47, 1726 (1993)
26.10 S.-S. Liaw, F.-Y. Chiou: Phys. Rev. A 49,2435
(1994)
26.11 G. Feldman, T. Fulton: Ann. Phys. (N. Y.) 201,193
(1990)
26.12 G. Feldman, T. Fulton, J. Ingham: Ann. Phys. (N. Y.)
219, 1 (1992)
26.13 A. Devoto, G. Feldman, T. Fulton: Ann. Phys. (N. Y.)
232, 88 (1994)
26.14 T. Fulton, W. R. Johnson: Phys. Rev. A34,1686
(1986)
26.15 T. H. Koopmans: Physica 1, 104 (1933)
26.16 L. Hostler: J. Math. Phys. 5, 1234 (1964)
26.17 R. A. Swainson, G. W. F. Drake: J. Phys. A: Math.
Gen. 24, 1801 (1991)
26.18 J. Schwinger: J. Math. Phys. 5, 1606 (1964)
26.19 R. A. Swainson, G. W. F. Drake: J. Phys. A: Math.
Gen. 24, 95 (1991)
26.20 S.-S. Liaw: Phys. Rev. A 48, 3555 (1993)
26.21 E. E. Salpeter: Phys. Rev. 87, 328 (1952)
26.22 S.-S. Liaw, F.-Y. Chiou: Phys. Rev. A 49, 2435 (1994),
Eq. (15)
26.23 G. Feldman, T. Fulton: Ann. Phys. (N. Y.) 201,193
(1990), Fig. 6
26.24 J. B. French, V. F. Weisskopf: Phys. Rev. 75,1240
(1949)
Part B 26

412 Part B Atoms
26.25 G. W. Erickson, D. R. Yennie: Ann. Phys. (N. Y.) 35,
271 (1965)
26.26 G. W. Erickson, D. R. Yennie: Ann. Phys. (N. Y.) 35,
447 (1965)
26.27 W. R. Johnson, G. Soff: At. Data Nucl. Data Tables
33,405(1985)
26.28 K. T. Cheng, W. R. Johnson, J. Sapirstein: Phys. Rev.
Lett. 66, 2960 (1991)
26.29 C. de Boor: A Practical Guide to Splines (Springer,
Berlin, Heidelberg 1987)
26.30 W. R. Johnson, J. Sapirstein: Phys. Rev. Lett. 57, 1126
(1986)
Part B 26
413
Quantum Elect
27. Quantum Electrodynamics
Quantum Electrodynamics (QED) is the underlying
theory of atomic and molecular physics. Despite
this generality, it is not necessary to use the full
theory in most atomic physics problems. This is
because in the nonrelativistic limit QED reduces to
the Schrödinger equation, and the extra physics in
QED is in general quite small, being suppressed by
powers of the fine structure constant α.Giventhe
difficulty of solving the Schrödinger equation with
high accuracy in most atomic physics situations,
these small corrections can usually be neglected.
The theory is however needed to explain small
deviations from the solution to the Schrödinger
equation in simple systems, in particular a single
electron in a constant magnetic field and few-
electron atoms. Larger deviations occur for highly
charged ions, and also for high-energy scattering
of electrons and photons. We note that a rather
extensive review of QED is available [27.1], and
refer the reader interested in more details to that
work. In addition, comparison with experiment is
made by Mohr in Chapt. 28, and thus is done here
only in selected cases.
27.1 Covariant Perturbation Theory .............. 413
27.2 Renormalization Theory
and Gauge Choices .............................. 414
27.3 Tests of QED
in Lepton Scattering ............................ 416
27.4 Electron and Muon g Factors ................ 416
27.5 Recoil Corrections ................................ 418
27.6 Fine Structure ..................................... 420
27.7 Hyperfine Structure.............................. 421
27.7.1 Muonium Hyperfine Splitting ...... 421
27.7.2 Hydrogen Hyperfine Splitting...... 422
27.8 Orthopositronium Decay Rate ............... 422
27.9 Precision Tests of QED
in Neutral Helium ................................ 423
27.10 QED in Highly Charged
One-Electron Ions................................ 424
27.11 QED in Highly Charged
Many-Electron Ions ............................. 425
References .................................................. 427
27.1 Covariant Perturbation Theory
QED combines relativity, electromagnetism, and quan-
tum mechanics. As the first two theories were well
understood when quantum mechanics was formulated,
the development of the the fundamental equations of
QED (after Dirac’s introduction of his relativistic equa-
tion for the electron) took place rapidly, being in place
in 1928 [27.2, 3]. However, it was recognized almost
immediately that when higher order perturbation theory
was considered, infinities associated with short wave-
lengths, known as ultraviolet divergences, were present,
and that this apparently predicted infinite shifts in spec-
tral lines. These difficulties were not overcome for two
decades, but at that time improvements in calculational
technology coupled with an understanding that the in-
finities could be grouped into renormalizations of the
electron’s mass, charge, and wave function and the pho-
ton’s wave function, led to the modern form of QED.
A central object in this form of the theory is the S-matrix.
To introduce it, we start with the Schrödinger equation,
i
∂
∂t
Ψ(t) = (H
0
+ H
I
)Ψ(t) (27.1)
where H
0
is the Hamiltonian of free electrons and pho-
tons (although this can be easily generalized to include
external potentials such as a nuclear Coulomb field),
and H
I
the electromagnetic interaction between them.
These Hamiltonians follow from the Lagrangian density
L = L
0
+L
1
,where
L
0
=
¯
ψ
0
(x, t)
γ
µ
p
µ
−m
0
ψ
0
(x, t)
−
1
4
F
0µν
(x, t)F
µν
0
(x, t) (27.2)
and
L
I
=−e
0
¯
ψ
0
(x, t)γ
µ
ψ
0
(x, t) A
µ
0
(x, t). (27.3)
Part B 27

414 Part B Atoms
The 0 subscripts in the above emphasize that the fields
and couplings are unrenormalized: renormalization will
be discussed in the next section. In addition
¯
ψ p
µ
ψ
is understood to represent
1
2
i
¯
ψ(∂
µ
ψ) −
1
2
i(∂
µ
¯
ψ)ψ,and
gauge fixing terms have been suppressed. By making
the unitary transformation
Ψ(t) ≡ e
−iH
0
t/
Φ(t), (27.4)
which transforms from the Schrödinger to the interaction
representation, and further defining the U matrix through
Φ(t) =U(t, −∞)Φ(−∞),
(27.5)
one finds an equation for this matrix
i
∂
∂t
U(t, −∞) =
ˆ
H
I
(t)U(t, −∞) (27.6)
where
ˆ
H
I
(t) = e
iH
0
t/
H
I
e
−iH
0
t/
. (27.7)
Solving this equation iteratively then gives for the
S-matrix, defined as S =U(∞, −∞),
S =
∞
n=0
(−i)
n
1
n!
∞
−∞
dt
1
···
∞
−∞
dt
n
× T
ˆ
H
1
(t
1
), ···
ˆ
H
1
(t
n
)
, (27.8)
where T is the time ordering operator. An initial state
consisting of free electrons, positrons, and photons will
then have an amplitude to scatter into a final state with
different momenta and perhaps different numbers of
particles given by the S-matrix. This amplitude can be
calculated using Wick’s theorem, and the result conve-
niently represented by Feynman diagrams. Lowest order
results of this procedure (tree approximation) describe
processes such as electron scattering, electron–positron
annihilation, etc. to fairly high precision. However, as
mentioned above, when higher terms in the perturbation
expansion are considered, diagrams containing closed
loops are encountered that are formally infinite, and
a renormalization program must be introduced.
27.2 Renormalization Theory and Gauge Choices
Before we discuss renormalization theory, we mention
that QED has the same freedom to choose gauge as
classical electromagnetism. We will discuss four gauges
that have been used in QED calculations, though there
is of course an arbitrary number. All of these gauges can
be defined through the photon propagator in momentum
space. If this is defined by
d
4
x e
−ik·x
0|T [A
µ
(x)A
ν
(0)]|0≡−i
G
µν
(k)
k
2
(27.9)
the Coulomb gauge is defined by
G
00
=−
k
2
k
2
,
G
ij
=−
δ
ij
−
k
i
k
j
k
2
,
G
i0
=G
0i
= 0 . (27.10)
While this gauge is particularly physical, with the
G
00
part directly corresponding to the instantaneous
Coulomb interaction and the G
ij
to magnetic interac-
tions, it is relatively difficult to work with. For ease of
calculation, the covariant gauges, defined by
G
µν
= g
µν
+β
k
µ
k
ν
k
2
(27.11)
are useful, particularly the case β = 0, the Feyn-
man gauge. Other values of β are β = 2, the Yennie
gauge [27.4], and β =−1, the Landau gauge. The former
has the advantage of controlling infrared divergences,
and the latter of controlling ultraviolet divergences.
Two of these infinities are first encountered when
the self-energy of a free electron is calculated in second
order perturbation theory. In order to deal with finite
quantities, we first must introduce a device to regulate
the high-frequency range of the integrations. This can
be done in a number of ways, among them Pauli–Villars
regularization [27.5]. In this method one modifies the
photon propagator to
1/q
2
→ 1/
q
2
−λ
2
−1/
q
2
−Λ
2
,
(27.12)
where λ is a photon mass that regulates infrared diver-
gences and Λ an ultraviolet cutoff mass. In this case
the self-energy operator is represented by the Feynman
diagram of Fig. 27.1a, and is, using Feynman gauge,
Σ( p) =−ie
2
d
4
k
(2π)
4
γ
µ
1
p− k −m
0
γ
µ
×
1
k
2
−λ
2
−
1
k
2
−Λ
2
.
(27.13)
Part B 27.2

Quantum Electrodynamics 27.2 Renormalization Theory and Gauge Choices 415
a) b) c)
Fig. 27.1a–c Ultraviolet divergent one-loop Feynman dia-
grams
Combining the two denominators together with a Feyn-
man parameter and carrying out the integration over k
then leads to
Σ( p) = δm
(2)
+ B
(2)
(p −m
0
) +Σ
F
( p), (27.14)
where
δm
(2)
=
3αm
0
2π
[
ln(Λ/m
0
) +1/4
]
(27.15)
and
B
(2)
=−
α
2π
[ln(Λ/m
0
) +2ln(λ/m
0
) +9/4] .
(27.16)
Σ
F
will not be given here, but the important point is
that it is ultraviolet finite. Thus the ultraviolet infinities
of QED are isolated in the first two terms, which are of
a very simple structure.
The next infinity is connected with the vertex func-
tion of Fig. 27.1b. This is defined by the equation
Γ
µ
=−ie
3
0
d
4
k
(2π)
4
γ
ρ
1
p− k −m
γ
µ
×
1
p
− k −m
γ
ρ
1
k
2
−λ
2
−
1
k
2
−Λ
2
.
(27.17)
While Γ
µ
is a fairly complicated function, its ultraviolet
divergent part is simply a multiple of γ
µ
. When the
electron momenta p and p
are equal and on shell, this
integral can be evaluated to be
Γ
µ
= e
0
γ
µ
L
(2)
(27.18)
where
L
(2)
=
α
2π
[ln(Λ/m) +2ln(λ/m) +9/4].
(27.19)
The fact that L
(2)
=−B
(2)
is a consequence of the Ward
identity [27.6].
The final infinity of second-order QED arises from
the vacuum polarization diagram of Fig. 27.1c. The
associated integral is
Π
µν
( p) =−ie
2
d
4
k
(2π)
4
Tr
×
γ
µ
1
p+ k −m
0
γ
ν
1
k −m
0
.
(27.20)
In this case the integral cannot be regulated as be-
fore, since there is no photon propagator to modify.
Instead one can subtract a similar integral with the
electron mass replaced by M. Vacuum polarization is
particularly sensitive to ultraviolet divergences, since the
nominal order of the divergence is quadratic. However,
gauge invariance requires Π
µν
( p) to have the structure
p
2
g
µν
− p
µ
p
ν
Π
p
2
, and if one considers only the
p
µ
p
ν
part of the vacuum polarization integral, the ultra-
violet divergence is only logarithmic. This divergence is
independent of the photon momentum p, and one can
write
Π
p
2
= C
(2)
+Π
finite
p
2
(27.21)
where
C
(2)
=
α
3π
ln
M
2
/m
2
0
(27.22)
and
Π
finite
p
2
=−
2α
π
1
0
dxx(1 −x)
×ln
1 −x(1 −x) p
2
/m
2
0
.
(27.23)
The four infinite quantities encountered in second order
perturbation theory are modified by higher order correc-
tions, but no new divergent structures arise. The basic
idea of renormalization is to note that these structures
are already present in the lowest order Lagrangian. We
now make the following definitions:
m = m
0
+δm , (27.24)
ψ(x) = Z
−1/2
2
ψ
0
(x), (27.25)
A
µ
(x ) = Z
−1/2
3
A
µ
0
(x ), (27.26)
and
e = e
0
Z
−1
1
Z
2
Z
1/2
3
. (27.27)
These correspond to an additive renormalization of the
electron mass and multiplicative renormalizations of
the electron and photon wave functions and the elec-
tron charge. Rewriting the original bare Lagrangian in
terms of these renormalized quantities then gives that
Lagrangian without the 0 subscripts, plus the following
counterterms:
L
CT 1
= Z
2
δm
¯
ψ(x, t)ψ(x, t), (27.28)
L
CT 2
=−e(Z
1
−1)
¯
ψ(x, t)γ
µ
ψ(x, t) A
µ
(x, t),
(27.29)
L
CT 3
=−
1
4
(Z
3
−1)F
µν
(x, t)F
µν
(x, t), (27.30)
Part B 27.2
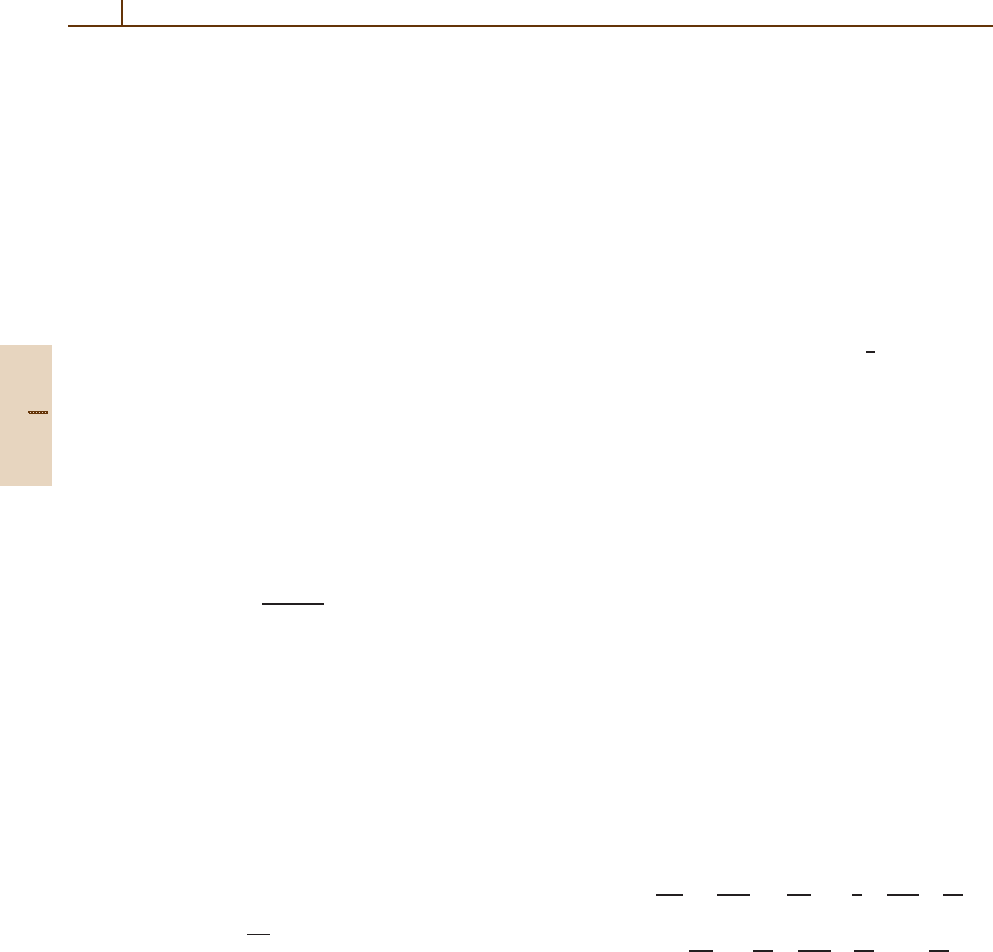
416 Part B Atoms
and
L
CT 4
= (Z
2
−1)
¯
ψ(x, t)
γ
µ
p
µ
−m
ψ(x, t).
(27.31)
By choosing Z
2
=1 + B
(2)
, Z
1
=1 −L
(2)
, δm =δm
(2)
,
and Z
3
= 1 −C
(2)
, these counterterms will precisely
cancel the previously encountered divergences in sec-
ond order. At this point we identify m and e as the
experimentally determined mass and charge of the elec-
tron: as long as these are used, the radiative corrections
discussed above have no effect for free electrons. How-
ever, when an electron undergoes scattering or is in the
presence of an external magnetic or nuclear Coulomb
field, the finite terms no longer vanish, and give rise to
small corrections. We now turn to a discussion of these
corrections.
27.3 Tests of QED in Lepton Scattering
The highest energy tests of QED come from scatter-
ing experiments at accelerators. While the dominant
part of QED corrections for all the other tests dis-
cussed in this chapter involves electron and photon
propagators close to the mass shell, scattering ex-
periments involve propagators very far off the mass
shell, which allows tests of the theory at very small
distances. It is standard to parameterize possible de-
viations from the predictions of QED at these small
distances by the introduction of form factors of the
form
F
q
2
= 1 −
q
2
q
2
−Λ
2
(27.32)
where q is photon momentum at an electron–photon
vertex. In QED Λ is infinite and this form factor is
unity even at very high q
2
, but this can be tested in
various scattering experiments. For example, Bhabha
scattering, e
+
e
−
→ e
+
e
−
, has been accurately meas-
ured at high center of mass energy,
√
s =34.8GeV, at
TASSO [27.1, 7]. To compare with QED, very sizable
radiative corrections must be carefully calculated, and
at these energies electroweak effects involving the Z bo-
son, while small, must also be considered. Although the
accuracy of the experiments is not high compared with
atomic physics measurements, being at the percent level,
the good agreement with QED that is found allows lower
limits on the cutoff Λ>500 GeV to be placed. This
corresponds to distances of under 10
−16
cm. It is of in-
terest to compare this sensitivity with that available from
atomic physics tests. The change in the photon propaga-
tor given above corresponds to a potential e
−Λr
/r.This
would lead to an energy shift of a 2s electron in hydro-
gen of 46/Λ
2
kHz with Λ in units of GeV. Thus even
1 kHz accuracy in the Lamb shift would only restrict
Λ>7GeV.
27.4 Electron and Muon g Factors
One of the successes of the Dirac equation is the pre-
diction g =2 for the electron. The leading correction to
this result coming from QED is the Schwinger correc-
tion [27.8],
g = 2
1 +
α
2π
.
(27.33)
While in principle this is an external field problem, be-
cause of the weakness of laboratory magnetic fields, the
correction can be related to Feynman diagrams with
free propagators. To see the weakness we note that
eB/m
2
e
= 2.3×10
−14
B (Gauss). In extremely intense
magnetic fields such as can be encountered in astrophys-
ical situations, a bound state approach [27.9] should be
used both for calculating energy shifts and the imag-
inary part of these shifts, which describe synchrotron
radiation. An example of the more precise approach
is Demeur’s formula for the (real) energy shift of an
electron in the lowest energy level
∆E =
mα
2π
−
eB
2m
2
+
eB
m
2
2
4
3
ln
m
2
2eB
−
13
18
+
eB
m
2
3
14
3
ln
m
2
2eB
−
32
5
ln 2 +
83
90
+···
.
(27.34)
The second term could actually be seen at the present
level of precision, but is spin-independent, and the third
term is negligible. An interesting feature of the experi-
ment is the effect of the conducting cavity, which must be
understood to extract the correct value of g −2 [27.1,10].
After the initial verification of the Schwinger correc-
tion, experiments of increasing precision culminating in
Part B 27.4

Quantum Electrodynamics 27.4 Electron and Muon g Factors 417
the Penning trap measurements in Washington [27.11]
have stimulated advances in theoretical calculations.
These involve the evaluation of constants C
i
defined
by
a
e
= C
1
α
π
+C
2
α
π
2
+C
3
α
π
3
+C
4
α
π
4
+···
(27.35)
where a
e
= (g −2)/2 is the anomalous magnetic mo-
ment of the electron. The computational effort involved
in computing the coefficients C
i
increases very rapidly
with i, and the four loop calculation is the largest QED
calculation ever carried out. The situation with regard
to these calculations is as follows. After the calcula-
tion of the Schwinger correction, the next step was the
evaluation of the seven Feynman diagrams of Fig. 27.2.
A feature of the one-loop calculation, that it is ultraviolet
finite, is no longer present at this level, and renormaliza-
tions of the self-mass, vertex, and wave function must
be performed, although the latter two cancel by Ward’s
identity. When the calculation is carried out in Feyn-
man gauge, each graph has an infrared divergence that
must be regulated in some fashion, for example by giv-
ing the photon a small mass λ. This calculation was
first correctly carried out by Sommerfield [27.12]and
Petermann [27.13]. The result is
C
2
=
197
144
+
π
2
6
(0.5 −3ln2) +0.75ζ(3)
(27.36)
where ζ(3) = 1.202 05 ... is the Riemann zeta func-
tion of argument 3. While each individual diagram is
infrared divergent in Feynman gauge, Adkins [27.14]
has used Yennie gauge [27.4] to recalculate the effect,
free of infrared divergent terms. His results are given in
Table 27.1.
The vacuum polarization graph of Fig. 27.2eplays
an interesting role. While the result for C
2
given above
a) b) c)
d) e)
Fig. 27.2a–e Two-loop Feynman diagrams contributing to
g −2
Table 27.1 Contributions to of C
2
in Yennie gauge
Graph Value
a −
1
2
B
(2)
−
3
16
b
5
4
ζ(3) −
5
6
π
2
ln 2 +
5
12
π
2
+
7
12
c −B
(2)
−
1
2
ζ(3) +
1
3
π
2
ln 2 −
29
24
d B
(2)
−
9
8
e −
1
3
π
2
+
119
36
Counterterm
1
2
B
(2)
includes only the case where the intermediate particles
in the loop are electrons, that loop can also involve any
charged particle, such as the muon, pion, or tau. How-
ever, because all these particles are much heavier than
the electron, which sets the energy scale of the Feyn-
man integral, their effect is suppressed by the square of
the mass ratio of the electron to their mass, and are thus
quite small. Specifically, in units of 10
−12
, the muon
loop contributes 2.80, the tau loop 0.01, and hadrons
1.6(2). These act to increase C
2
by 0.000 000 82. We
note in passing that the effect of the weak interac-
tions enters in one loop, and contributes 0.05 × 10
−12
to the electron g −2 value and 1 95( 10) ×10
−11
for the
muon.
When the anomalous magnetic moment of the muon
is considered the situation changes significantly. Firstly,
the contribution of electrons in the loop is enhanced,
since they are now relatively light particles, and the vac-
uum polarization loop behaves as a logarithm of the mass
ratio. Specifically, the difference between the muon and
electron g −2 factors behaves as [27.15]
a
µ
−a
e
= 1.094
α
π
2
+22.9
α
π
3
+132.7
α
π
4
+··· (27.37)
These large coefficients arise primarily because the vac-
uum polarization loops involving electrons change the
effective value of α to α/(1 −2α/3π ln m
µ
/m
e
).Note
however that such logarithmic terms also arise from
other sources, most notably the light-by-light scattering
graphs that enter first in third order.
The second important change in the muon case is
the significant role of strongly interacting particles in
the loop. Fortunately, while our present inability to carry
Part B 27.4

418 Part B Atoms
out high accuracy calculations of the strong interactions
could in principle interfere with the interpretation of the
muon g −2asaQED test, the bulk of this contribution
can be related to the experimentally available cross-
section for e
+
e
−
annihilation into hadrons [27.16]. It
is also possible to use τ decay to determine the con-
tribution [27.17]. At present the two methods are not in
agreement, and this situation will have to be resolved be-
fore a possible discrepancy between theory and the most
recent experiment [27.18] can be interpreted as indicat-
ing new physics. Specifically, if the τ data is used a 1.4
standard deviation difference exists, but if the e
+
e
−
data is used the discrepancy increases to 2.7 standard
deviations.
The calculation of C
3
involves 72 Feynman graphs,
although they can be grouped together into a smaller
number of gauge invariant sets. As discussed in more
detail in Chapt. 28, C
3
is now known analytically, re-
moving an important source of numerical uncertainty.
The evaluation of such high-order graphs requires an in-
tricate set of subtractions to lead to finite answers, and
provides a practical demonstration of the renormaliz-
ability of QED. The result for C
3
is
C
3
= 1.181 241 456 ... (27.38)
Finally, the very large scale calculation of C
4
,whichis
almost completely numerical, has been carried out by
Kinoshita and Lindquist [27.19]. When their result,
C
4
=−1.509 8(384), (27.39)
is compared with experiment, agreement is found, but
the largest source of error is the uncertainty in the
fine structure constant as determined from solid state
physics. However, if one instead assumes the validity of
QED, the situation can be turned around to determine
a QED value of the fine structure constant. This is done
by combining the experimental result [27.11]
a
e
−
= 1 159 652 188.4(4 .3) ×10
−12
a
e
+
= 1 159 652 187.9(4 .3) ×10
−12
(27.40)
with the previous formulas for the C coefficients (in-
cluding the small vacuum polarization corrections for
C
2
discussed above). The result is
α
−1
QED
= 137.035 992 22(51)(48) (27.41)
where the errors come from experiment and C
4
respec-
tively. It would be of great interest to have another QED
determination of the fine structure constant of com-
parable accuracy: a very promising approach involves
precision measurements of recoil in cesium [27.20, 21],
which has achieved 7 ppb and has the potential of reach-
ing 1 ppb. Another way to determine α involves the fine
structure of helium, as will be discussed below.
27.5 Recoil Corrections
Because of the smallness of the ratio of the electron
mass to most nuclear masses, a reasonable approxi-
mation to atoms is to treat the nucleus as a source of
a classical Coulomb and magnetic dipole field, which
corresponds to the use of Furry representation [27.22].
In addition, the leading correction to this approximation
can be accounted for by using the reduced mass in place
of the electron mass. However, to calculate higher order
terms consistently, one must treat a one-electron atom as
a two-body system and an N-electron atom as a N +1-
body system. Shortly after the development of modern
QED, a number of workers [27.23–25] developed two-
body equations by considering the Green’s function for
electron–nucleus scattering, with the original equation
known as the Bethe–Salpeter equation. Considered as
a function of the total energy in the c.m. frame, this
Green’s function has poles at bound state energies. In
practice an approximate Green’s function is considered
that has poles at either the Schrödinger or the Dirac en-
ergies, with reduced mass built in to some degree. Then
a perturbation theory is set up that allows corrections
of higher order in α and m
e
/m
N
to be calculated in
a systematic way.
While the treatment of recoil using various versions
of the Bethe–Salpeter equation gives correct answers,
its implementation is quite complicated. In recent years
enormous progress has been made using the very differ-
ent approach of effective field theory. One of the earliest
uses of effective field theory was in QED [27.26], and
we will refer to it as NRQED (nonrelativistic QED).
Effective field theories have been used in many differ-
ent areas of physics, and are useful whenever physics
at one scale can be treated separately from physics at
a widely different scale. Atomic physics is an ideal place
for the use of effective field theory, as, for example, the
scale of the Bohr radius, the basic atomic physics length
scale, is separated from the electron Compton wave-
length, which is characteristic of most QED effects, by
two orders of magnitude. NRQED applies to both recoil
and non-recoil QED corrections, and always has as its
Part B 27.5
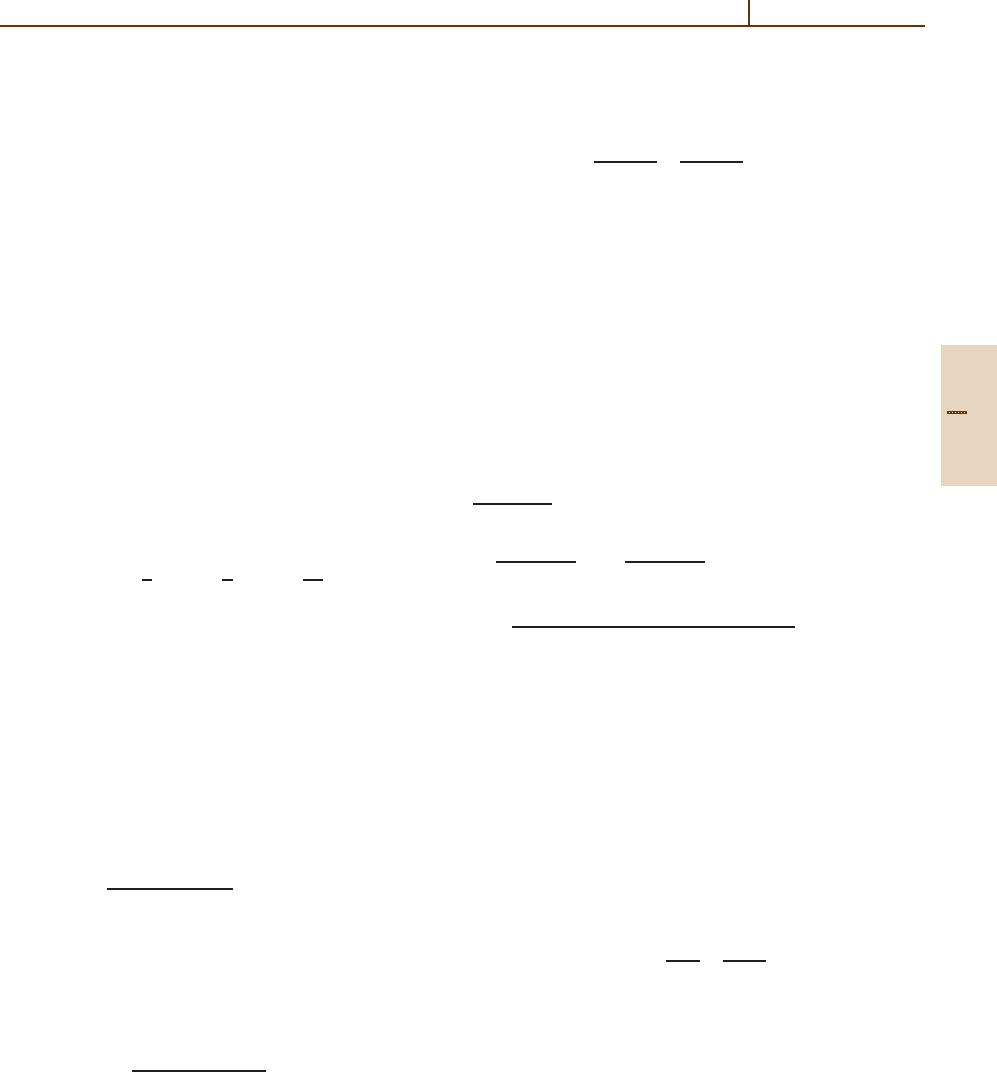
Quantum Electrodynamics 27.5 Recoil Corrections 419
starting point the well-understood Schrödinger equation.
Relativistic effects, such as relativistic mass increase,
magnetic interactions, or the Darwin term, are then in-
cluded perturbatively. This requires cutoff methods to
deal with higher orders of perturbation theory, where
those operators lead to ultraviolet singular results. In ad-
dition, the short distance physics of QED is accounted
for by adding in perturbations that involve delta func-
tions or derivatives of delta functions, with coefficients
determined by what is called a matching procedure, in
which scattering calculations in full QED and in the ef-
fective field theory are forced to agree. This approach,
which unfortunately has not yet been treated at text-
book level, has had a very great impact on higher order
QED calculations, with a number of higher order effects
calculated in recent years using the technique.
To illustrate the method, we follow a treatment of
Pachucki [27.27] in which the Dirac energies of hydro-
gen in the non-recoil limit are calculated to order mα
6
.
While he treated the general case, for simplicity we con-
sider here only the ground state energy, which has the
Taylor expansion
E = mc
2
1 −
1
2
(Zα)
2
−
1
8
(Zα)
4
−
1
16
(Zα)
6
,
(27.42)
where we follow the convention of allowing for a general
nuclear charge Z. The fine structure, as is well known,
can be derived from perturbations associated with the
relativistic mass increase and the Darwin term, with
the spin–orbit interaction not contributing for s-states.
While the contribution of these perturbations is finite
in lowest order perturbation theory, they give rise to
singularities when treated in second order. To see this,
we give the momentum space version of second order
perturbation theory,
E
(2)
=
d
3
p d
3
k d
3
l d
3
q
(2π)
9
φ
0
( p)V(p, k)
× G
R
(k, l)V(l, q)φ
0
(q), (27.43)
where G
R
is the reduced Coulomb Green’s function.
It can be expanded in terms of a free term, a one-
potential term, and a many-potential term. The strongest
singularities are associated with the free term,
G
0
R
(k, l) =−
(2π)
3
2mδ
3
(k−l)
k
2
+γ
2
, (27.44)
where γ = mZα. The Darwin term in momentum space
is simply V
D
= πZα/2m
2
, and it is simple to see that
when both V
s in the expression for E
(2)
are Darwin
terms and the free part of the Green’s function is used
a linearly divergent integral results. This can be regulated
by imposing a cutoff Λ on the magnitude of all momenta
in the integral, in which case a simple calculation gives
E
(2)
(DD0) =−
Λ(Zα)
5
4π
+
m(Zα)
6
8
.
(27.45)
Linear divergences also exist when two relativistic mass
increase (RMI)termsorDarwin-RMI cross terms are
considered, but these terms happen to cancel.
To get a finite answer, the contribution of oper-
ators of intrinsic order m(Zα)
6
must be considered.
These operators can be obtained from consideration of
the Bethe–Salpeter equation, but a great simplification
of NRQED is the fact that they can also be obtained
by considering free-particle scattering, where the com-
plications of the bound state problem are not present.
We illustrate this by considering electron scattering in
a Coulomb potential created by a stationary charge Z|e|.
In the Dirac theory this is given by
−4πZα
|p
2
− p
1
|
2
¯
ψ(p
2
)γ
0
ψ( p
1
)
=
−4πZα
|p
2
− p
1
|
2
1 −
|p
2
− p
1
|
2
8m
2
+
6|p
2
− p
1
|
2
p
2
1
+ p
2
2
+5
p
2
2
− p
2
1
2
128m
4
.
(27.46)
In the above we have carried out a Taylor expansion
to fourth order in the electron momenta and dropped
spin–orbit terms. While this coincides with Schrödinger
theory in lowest order, a set of extra terms exists in the
Dirac case. To account for these, we modify the nonrel-
ativistic theory by adding extra operators that make the
theories agree. If the Taylor expansion is stopped in or-
der p
2
, we recognize the Darwin term already treated
above, but to go to order m(Zα)
6
the last terms must
be treated. They are again linearly divergent, as are two
other terms – one associated with the next term in RMI,
V
RMI
=−(2π)
3
δ(k−l)
|k|
4
8m
3
−
|k|
6
16m
5
(27.47)
and the other a term that can either be derived with
a Foldy–Wouthuysen transformation or by compar-
ing two-Coulomb photon scattering in the Dirac and
Schrödinger theories. When combined, first order per-
turbation theory for these operators cancels out the linear
divergence found above arising from second order per-
turbation theory, along with a logarithmic singularity,
leaving a finite answer in agreement with the Dirac
theory.
Part B 27.5
