Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

1373

Charged-Parti

91. Charged-Particle–Matter Interactions

In the description of the interaction of fast

charged particles with matter, two aspects can be

distinguished: the effects on the particle, usually

energy losses and deﬂections, and the spatial

distribution of the energy lost by the particle in

the absorber.

This Chapter discusses concepts needed in

the operation of charged particle detectors

and in describing radiation effects (Chapt. 92).

Speciﬁcally, the radiation effects used for the

instantaneous observation (i. e., within fractions

of a millisecond) of the passage of a charged

particle are described. Delayed effects, such

as chemical reactions (e.g., biological effects,

chemical dosimeters, photographic emulsions),

metastable states, etc. are not discussed. It

is assumed that particle speeds have been

determined with, e.g., magnetic analyzers or by

measurement of the time of ﬂight. A measurement

of particle ranges can also be used to determine the

initial speed. The description is restricted to fast

charged particles, deﬁned by speeds v>6v

the Bohr speed), or β = v/c > 0.04. Interactions

and cross sections at smaller speeds are discussed,

e.g., by Rudd et al.[91.1] and in [91.2].

The present Chapter primarily considers energy

loss straggling, rather than the stopping powers

discussed by Fano [91.3].

91.1 Experimental Aspects ...........................1374

91.1.1 Energy Loss Experiments

and Radiation Detectors.............1374

91.1.2 Inelastic Scattering Events..........1375

91.2 Theory of Cross Sections .......................1376

91.2.1 Rutherford Cross Section ............ 1376

91.2.2 Binary Encounter

Approximation..........................1376

91.2.3 Bethe Model of Cross Section ...... 1377

91.2.4 Fermi Virtual Photon Method ...... 1377

91.3 Moments of the Cross Section ...............1378

91.3.1 Total Collision Cross Section M

...1378

91.3.2 Stopping Power M

....................1379

91.3.3 Second Moment M

...................1380

91.4 Energy Loss Straggling .........................1381

91.4.1 Straggling Parameters................1381

91.4.2 Analytic Methods

for Calculating Energy Loss

Straggling Function ...................1382

91.4.3 Particle identiﬁcation (PID)......... 1384

91.5 Multiple Scattering

and Nuclear Reactions .........................1384

91.6 Monte Carlo Calculations ......................1384

91.7 Detector Conversion Factors..................1385

References .................................................. 1385

It is important to understand that the mean energy-loss

is not a suitable concept to use in the description of

energy-loss spectra for thin absorbers. The most prob-

able energy-loss should be used instead. The methods

described here can be used to calculate reliable data

for detector applications. No attempt is made to present

a complete review. Anecdotal, qualitative examples of

various effects are described. The following deﬁnitions

are used:

1. The number of atoms or molecules per unit vol-

ume N = N

/A, with A the molecular weight

(in g/mole) of the absorber (with Z

electrons per

molecule),  its density, and N

is Avogadro’s

number;

2. The relativistic factors β and γ for particles with rest

mass M

, speed v = βc and kinetic energy T :



T /M



2 +T /M





1 +T /M



γ = M/M

= 1 +T /M

= 1/



1 −β



= γ

−1 ;

Part G 91

1374 Part G Applications

3. The coefﬁcient of the Rutherford equation:

2πZ

= 2πr

= 2.549 55 × 10

−19

eV c m

, (91.1)

where m

is the rest mass of an electron, −e its

charge, Z

e the charge of the incident particle, and

= α

is the classical electron radius; and

4. The maximum energy loss of a heavy particle to an

electron: E

max

∼ 2m

[91.4].

91.1 Experimental Aspects

91.1.1 Energy Loss Experiments

and Radiation Detectors

After passing through a thickness x of material, an

initially monoenergetic beam of particles acquires a dis-

tribution of energies described by a probability density

function

F(∆) =

dN (∆)

d∆

(91.2)

where ∆ is the energy loss per particle, and dN (∆)

is the number of particles in the range ∆ to ∆ + d∆.

The straggling function F(∆) represents the spectrum

of energy losses ∆, such that



F(∆) d∆ = N , the total

number of particles observed. It can be characterized by

the quantities

1. the most probable energy loss ∆

2. the full width at half maximum Γ ,

3. the moments [91.8]



F(∆)∆

d∆, (91.3)

and the central moments



F(∆)(∆ −µ

)

d∆. (91.4)

Then µ

=∆ is the mean energy loss, C

= σ

the variance and γ

= C

3/2

is the skewness. The

ﬂuence spectrum φ(T ) is the complementary function

describing the distribution of residual energies T of the

particles.

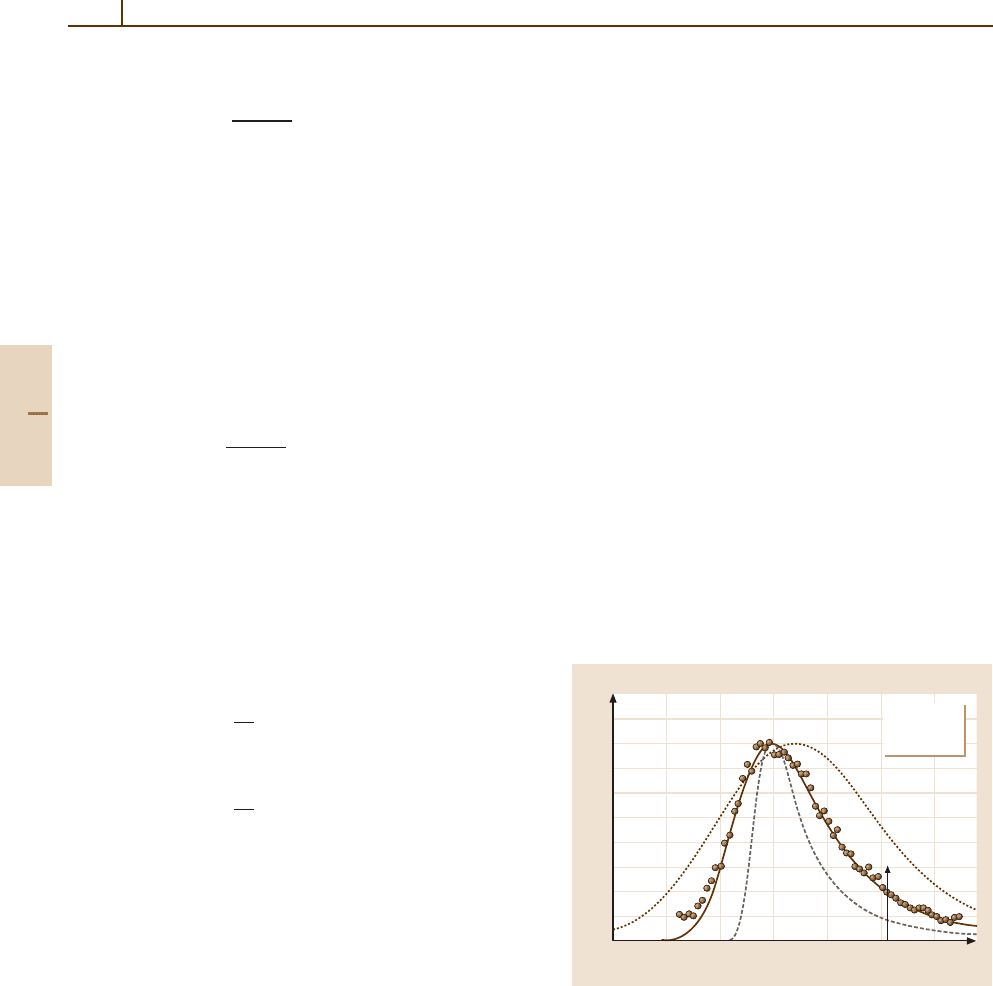
As an example, Fig. 91.1 shows F(∆) d∆ for

1.27 GeV protons passing through a 32 µm thick silicon

wafer [91.5]. The measured quantity is the ionization J

resulting from the creation of electron–hole pairs in the

silicon, so that ∆ = JW is the energy deposited, where

W is the energy required to create an electron–hole pair.

For ∆<15 keV, the energy deposited differs little from

the energy lost by the protons. For larger ∆, some of the

secondary electrons may escape from the silicon, mak-

ing the apparent energy deposited less than the energy

lost [91.9]. The spectrum has a long tail extending up to

a maximum energy loss of 4.6 MeV. This accounts for

the large value of ∆=12.8 keV, and the even larger

value C

1/2

= 43 keV for the standard deviation, relative

to ∆

= 7.4keVandΓ = 5.2keV.

In losing energy, the beam particles also suffer an-

gular deﬂections, but for heavy particles, the deﬂections

are usually small. For electrons, angular deﬂections are

quite important, and are discussed in Chapts. 47, 64,

and 65. Nuclear reactions cause large effects but are

quite infrequent. Further examples of straggling spec-

tra are given in [91.5, 10–12] for thin, extremely thin,

moderately thick, and thick absorbers respectively.

Only for thick absorbers, the stopping power

S(T ) =−dT /dx (i. e., the mean energy lost per unit

thickness) provides a convenient measure of the energy

loss process. For a beam with incident energy T

and

250

200

150

100

∆(keV)

0 5 10 15

dN(∆) = F(∆)d∆

<∆>

1.27 GeV p

32 µm Si

N = 6000

Fig. 91.1 Energy loss straggling functions F(∆) d∆ for

1.27 GeV protons traversing a 32 µm silicon detector, with

d∆ = 0.21 keV. The experimental data are shown by cir-

cles. Three calculated functions normalized to the same

peak height are shown for comparison [91.5]. The solid line

was calculated with the Bethe cross section Fig. 91.3 with

∆

=7.4keV,Γ =5.2keV,and∆=12.8keV.Thebro-

ken line is the Landau function [91.6]andthedotted line is

the Blunck–Leisegang modiﬁcation [91.7]

Part G 91.1

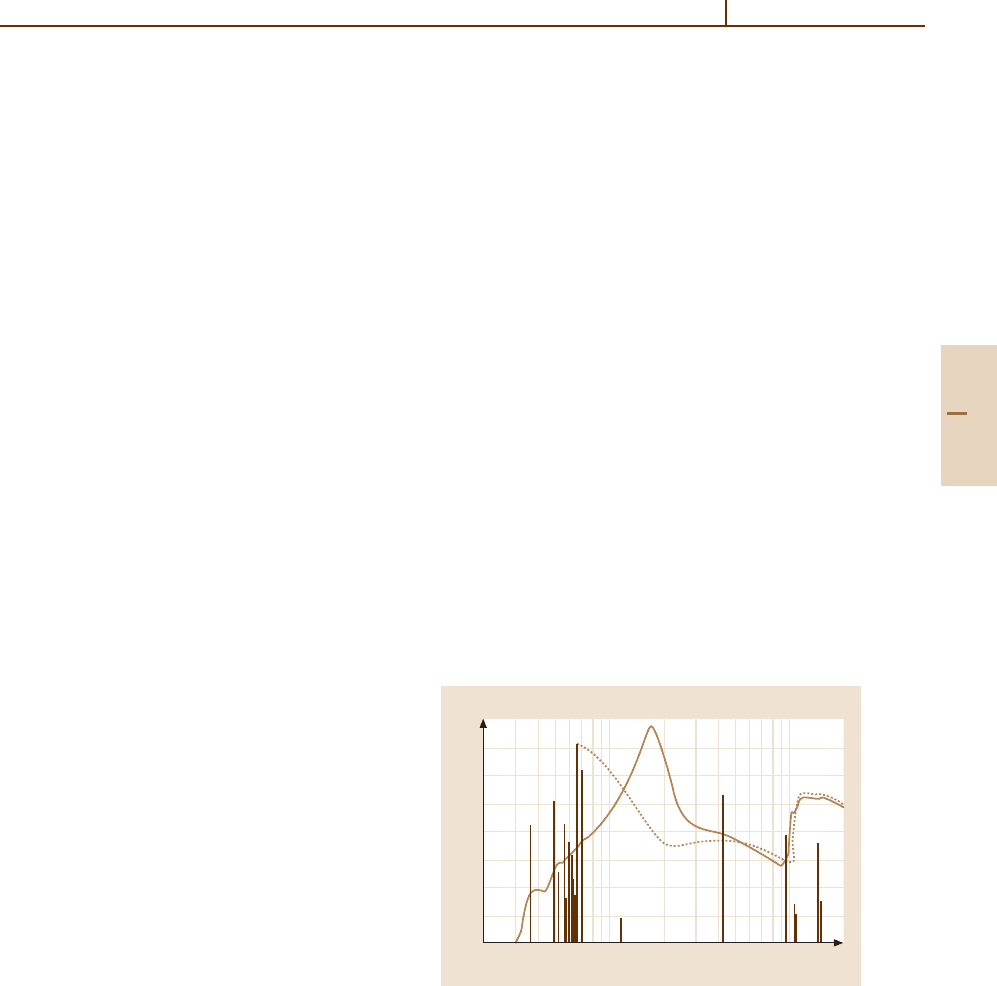
Charged-Particle–Matter Interactions 91.1 Experimental Aspects 1375

∆ < 0.1T

, S(T ) is often approximated by

S(T

−∆/2) ∆/x , (91.5)

provided that x  a

(Sect. 91.4). The stopping power

S(T ) depends on the absorber properties, especially

the electron density NZ

. The radiation dose D(x) at

a distance x into the material is given by

D(x) =



φ(T , x)S(T )dT ,

(91.6)

where φ(T , x) is the ﬂuence spectrum. D(x) is used in

radiation dosimetry and protection [91.15, 16].

S(T ) ceases to be useful for very thin absorbers,

such as microscopic biological specimens, micro- or

nano-devices, or thin ionization chambers. Instead ∆

and Γ should be used. No simple equations can provide

∆

and Γ . They must be found from calculated or

experimental F(∆). Calculations of F(∆) are described

in 91.4.2 and 91.6.

A detailed theoretical description of the energy de-

position process requires cross sections for the various

scattering events in the target, the most important being

collisions with electrons. The Rutherford cross section

for the collision of a particle with a free electron is only

useful for ∆

 30 U

,whereU

is the binding energy

of a target electron (∼ 500 eV for outer shell electrons).

Various modiﬁcations to the Rutherford cross section

for smaller ∆ are discussed in Sect. 91.2.

91.1.2 Inelastic Scattering Events

If a beam of N monoenergetic particles with speed v

passes through an absorber of inﬁnitesimal thickness dx,

the average number of particles experiencing a collision

with energy loss between E and E + dE is given by

dN (E) = N Nσ(E) dE dx ,

(91.7)

where σ(E) is the collision cross section per molecule

differential in E; it depends on β. Using this equation,

σ(E) can be obtained from measurements [91.17, 18]

with extremely thin absorbers where particles on the

average suffer less than one collision. If particles pass

through a thicker absorber, they make several collisions

with energy losses E

; and the total energy loss is ∆ =



(Sect. 91.4.2).

Large differences exist between a gas and a solid

of the same composition due to changes in the va-

lence shell electrons. In isolated atoms [91.14], the

smallest energy losses are to discrete excited electronic

states. Ionizations occur for energy losses exceed-

ing the binding energies U

for each atomic shell l

and the released electrons are given a kinetic energy

δ = E −U

. For ionization, energy losses are contin-

uous (Fig. 91.2). If atoms are brought closer together

to form a liquid or a solid, their valence electrons

come under the inﬂuence of the cores of surround-

ing atoms. A core is deﬁned to consist of the nucleus

and all the electrons inside the valence shell. For C,

O, or H

O, the core consists of two electrons in the

K-shell, for Al or Si it contains two electrons in the

K-shell and eight electrons in the L-shell. For metals,

the valence electrons form a conduction band where

they are nearly free. If a charged particle moves through

the solid, the transfer of very small energies to the

electron by Rutherford scattering is not observed. In-

stead, many thousands of them are excited at a time.

For metals, this process is called plasmon excitation,

for insulators, collective excitation (Fig. 91.2). For most

substances, the plasmon excitation energy E

is much

larger than the energy of the lowest excited state of

the atom E

. For example, for Be, E

= 3.6 eV [91.13],

while E

= 19 eV [91.17]. Similarly, for silicon,

= 3.6 eV [91.13]andE

= 16.7 eV [91.5].

For molecules, measurements of electron energy

losses [91.18] provide information about the difference

in the structure of σ(E) between gas and solid. For ex-

ample, for benzene (C

) the vapor shows distinct

structures for excitations to several discrete states, and

–1

–2

–3

–4

2 5 10 20 50 100 200

f(E O)(eV

–1

)

E(eV)

solid, I = 174 eV

gas,

I = 131 eV

ln I =  f( ) ln d

⑀⑀⑀

Fig. 91.2 Comparison of the dipole oscillator strength spec-

tra for atomic and solid silicon. Discrete atomic excitations

are shown by vertical lines, continuum excitations by

the dotted line. Data for the atom are based on calcula-

tions [91.13]. Data for the solid are from [91.5]. The broad

peak at ≈ 17 eV represents the plasmon excitations. Uncer-

tainties may exceed 10%. The discrete atomic excitations

disappear in the solid. The photoionization cross section is

σ(E) = 109.8 f(E) Mb [91.14]

Part G 91.1

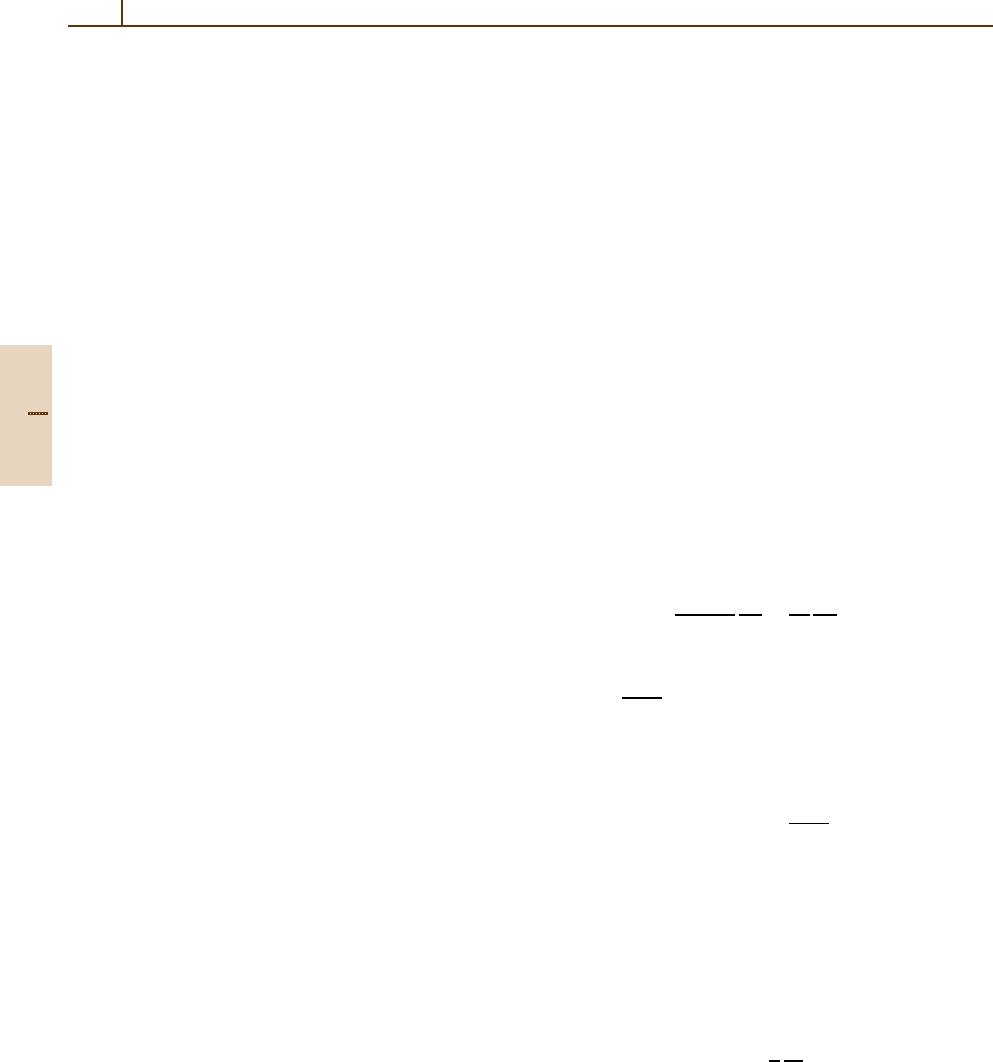
1376 Part G Applications

a broad peak at about 16 eV which appears to be equiva-

lent to a collective excitation. For the solid, the structures

are broadened, and the major peak for the collective ex-

citations shifts to 21 eV. Data for water can be found

in [91.19].

For energy losses well above E

, σ(E) decreases

smoothly until the ionization energy of the next electron

shell is reached, as shown in Fig. 91.2. In a molecular

substance such as CaCO

, several broad peaks appear

between 7 and 40 eV, followed by narrow peaks at 280 eV

(carbon K-shell), 345 eV (Ca L-shells), 530 eV (oxygen

K-shell) and 4 keV (Ca K-shell) [91.17].

While there are large changes in the structure of

the excitation of the valence electrons as the atoms

are coalesced into a solid (Fig. 91.2), changes are less

important for the inner shells because the binding en-

ergies of these shells are much larger than chemical

energies. As an example, for an amorphous thin car-

bon ﬁlm, the K-edge is at 284 eV [91.17], and K-shell

excitation shows essentially just one peak at ≈ 296 eV.

For the three biologically important molecules adenine,

uracil and thymine, several peaks appear [91.20], all

located between 284 and 300 eV. Thus there is at most

a small change in the energy of the K-shell excitation, but

the number of peaks as well as their locations changes

considerably. For Al above the K-edge (1.56 keV),

a structure with several peaks appears [91.21], with

separations of about 40 eV. This structure, called ex-

tended X-ray absorption ﬁne structure (EXAFS) [91.22],

is caused by the presence of nearby atomic cores

which backscatter the photoelectrons and thus change

their wave functions. The discrete excitations of the

atom below the K-edge disappear completely. Thus

solid state and chemical effects are very important

for valence shell electrons, and less so for inner-shell

electrons.

91.2 Theory of Cross Sections

The cross section for the collision of two free

charged particles is given by the Rutherford ex-

pression. If charged particles collide with electrons

bound in atoms, molecules or solids, the cross sec-

tion can be written as a modiﬁed Rutherford cross

section. A plausible way of describing these interac-

tions is to consider the emission of virtual photons

by the fast particle, which then are absorbed by

the material in the Fermi virtual photon method

(FVP) [91.23]. The collision cross section then is pro-

portional to the photo absorption cross section of the

molecules. Bohr [91.24] described this as a “resonance”

effect.

A variety of models has been used to obtain theoret-

ical σ(E) for bound electrons. Here, three of them will

be described and compared with each other. Examples

are shown in Fig. 91.3. Few analytic functions and meth-

ods are available to calculate cross sections (Chapt. 47).

Usually, numerical calculations must be made to obtain

reliable data for real absorbers.

91.2.1 Rutherford Cross Section

The cross section for close collisions of fast charged

particles with loosely bound electrons is well approxi-

mated by the cross section for the collision of a charged

particle with a free electron at rest. The nonrelativistic

Rutherford cross section σ

(E) foranenergylossE in

the collision of a charged particle with speed v in the

laboratory frame is given by [91.25–28]

(E) =

2πZ

. (91.8)

Since the secondary electron receives all the energy E

lost by the incident particle, the momentum transfer is

q =

√

2mE. The cross section σ

(E) does not depend on

particle mass M. The leading relativistic correction (For

γ>M/m, further terms must be included [91.29–31])



(E) = σ

(E)



1 −β

max



. (91.9)

91.2.2 Binary Encounter Approximation

A simple correction to σ

(E) can be achieved by tak-

ing into account the velocity of the bound electrons.

With binding energy U

, average kinetic energy T

,and

average speed u of the electrons, the expression is

(E) = σ

(E)



1 +



, E > U

, (91.10)

which is valid for v  u. The total cross section

for a molecule includes contributions from each elec-

tron shell. Variants of this approach are described

in [91.32, 33]. Figure 91.3 shows an example.

Part G 91.2

Charged-Particle–Matter Interactions 91.2 Theory of Cross Sections 1377

10.0

10 30 100 300 1000 3000 10000

30000

100000

4.0

2.0

1.0

0.4

0.2

0.1

σ( )/ ( )

⑀⑀

␳

(eV)

⑀

Fig. 91.3 Inelastic cross sections σ(E) for single colli-

sions in solid silicon, for incident protons with an energy

T = 100 MeV, calculated using different theories. The hor-

izontal line at 1.0 represents the Rutherford cross section

from (91.8). The other curves are Bethe theory (solid line);

FVP approximation (dashed line); binary encounter ap-

proximation from (91.10) [91.32](dotted line). The curves

extend to E

max

= 230 keV

91.2.3 Bethe Model of Cross Section

The Bethe model [91.34] derives from the ﬁrst Born ap-

proximation for inelastic scattering, which becomes es-

sentially exact at high energies. In terms of the inelastic

form factor |F (E, K)|

, the energy loss cross section is

dσ(E, Q) = σ

(Q)|F (E, K)|

dQ , (91.11)

where Q = q

/2m

,and K is the momentum trans-

fer vector. The generalized oscillator strength (GOS)is

deﬁned by

f(E, K) = E|F (E, K)|

/Q , (91.12)

such that f(E, K) reduces to the optical dipole oscillator

strength f(E, 0) ≡ f(E) in the limit K → 0. Then

dσ(E, Q) = σ

(E)Ef(E, K) dlnQ . (91.13)

For hydrogenic atoms, f(E, K) is well known

[91.34–38], and a model spectrum is shown in Fig. 10

of [91.27, 28]. For more complicated atoms, many-

electron effects introduce small corrections, as shown

in Fig. 91.4 for Si using a Hartree–Fock approxima-

tion. Adding the contributions from all shells yields

the Bethe result in Fig. 91.3 [91.5]. Similar results are

given in [91.39] for Al. For the outermost electrons in

metals, the electron gas model can be used to generate

cross sections [91.40–42]. For semiconductors and insu-

lators a model has been derived using the tight binding

approximation for the ground state wave function and

orthogonalized plane waves for excited states [91.41].

The dipole oscillator strength is derived from the data

for optical absorption coefﬁcients; for solids [91.43]and

gases [91.44–46] see Chapt. 61.

91.2.4 Fermi Virtual Photon Method

In the Fermi virtual photon (FVP) method, f(E, K) is

approximated by f(E, 0) for Q < E, with a delta func-

tion at Q = E [91.23, 47–50](Fig.91.4). Then σ(E) is

given by [91.48]

σ(E) = σ

(E)



Ef(E, 0) ln



2mv





f(E



, 0) dE





(91.14)

andsoonly f(E) need be known, or equivalently

Im(−1/),where is the complex dielectric constant

of the absorber. Data can be extracted from a variety of

optical measurements [91.43,44, 51], and from electron

0.12

0.10

0.08

0.06

0.04

0.02

0.00

K(a.u.)

024 68101214

f(E, K)(Ry

–1

)

E = 48 Ry

Fig. 91.4 Generalized oscillator strength (GOS) f(E, K)

(solid line) for longitudinal excitations of the 2p-shell of Si

atoms (with a binding energy U

= 8 Ry), calculated with

the Hartree–Fock–Slater potential. The energy transfer is

E = 650 eV. The hydrogenic approximation is given by the

broken line; f(E, K) peaks at (Ka

)

≈ E −U

.Inthe

FVP model, (91.14), the GOS is replaced by a δ-function at

= E

1/2

and by f(E, 0) for 0 < Ka

< E

1/2

(straight

lines)

Part G 91.2

1378 Part G Applications

energy loss measurements [91.52]. A cross section cal-

culated with this model is given in Fig. 91.3.Theσ(E)

differ by as much as 50% from the Bethe result, but the

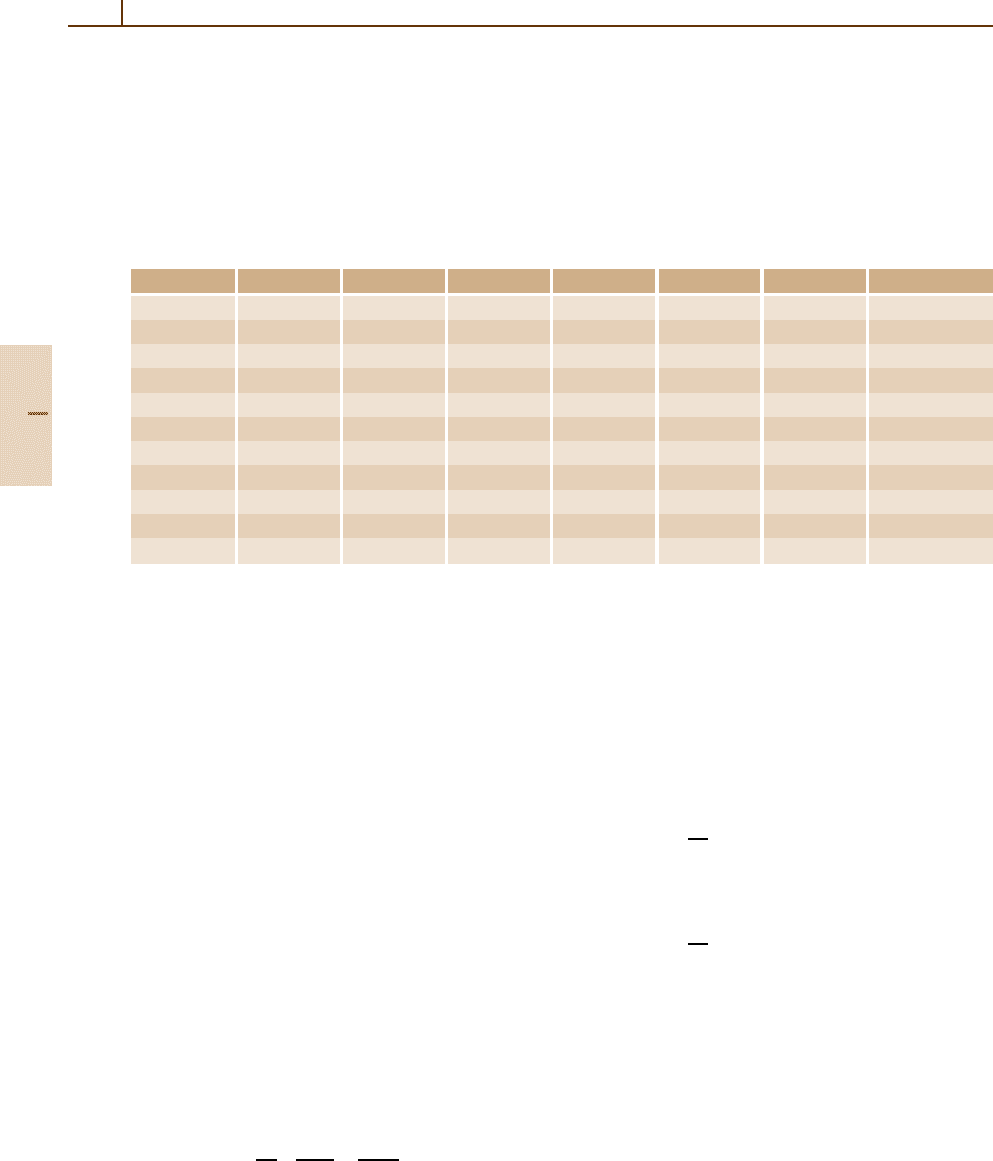
Table 91.1 The coefﬁcient τ(β) = M

/(NZk

) for pions with M

= 139.567 MeV/c

, calculated in the FVP approxi-

mation. For comparison, the Si (GOS) results were calculated from the complete F(E, K) generalized oscillator strengths.

The estimated accuracies are ≈ 1% for Si (GOS)and∼ 30% for the others. The values are the same for all heavy par-

ticles with the same β; they differ slightly for electrons. For Si



 =2.329 g/cm



, NZk

= 17.82 eV/µm, for the gases

(at STP), NZk

= 6.3828 Z eV /cm. Units of τ(β) are eV

−1

T (MeV) β Si(GOS) Si He Ar Ethane Butane

UT 1. 0.11907 0.1208 0.1333 0.1937 0.1081 0.2961 0.2855

3. 0.20406 0.1408 0.1528 0.2229 0.1242 0.3379 0.3259

10. 0.35950 0.1612 0.1738 0.2538 0.1412 0.3821 0.3686

30. 0.56791 0.1792 0.1917 0.2802 0.1557 0.4198 0.4050

100. 0.81276 0.1957 0.2082 0.3093 0.1717 0.4614 0.4451

300. 0.94825 0.2061 0.2186 0.3441 0.1908 0.5111 0.4931

1000. 0.99247 0.2127 0.2252 0.3958 0.2189 0.5843 0.5637

3000. 0.99901 0.2150 0.2275 0.4499 0.2468 0.6580 0.6333

10000. 0.99991 0.2155 0.2280 0.5057 0.2671 0.7034 0.6646

30000. 0.99999 0.2156 0.2281 0.5332 0.2737 0.7111 0.6697

100000. 1.00000 0.2156 0.2281 0.5407 0.2765 0.7128 0.6709

moments differ by at most 10% (Table 91.1). It is ev-

idently a better approximation than that given by the

binary encounter approximation of (91.10).

91.3 Moments of the Cross Section

Various moments of σ(E) are deﬁned by [91.5, 53]

≡ N



σ(E) dE . (91.15)

where the range of integration covers all non vanish-

ing σ(E), including a summation over discrete excited

states. Then M

= Nσ

tot

= 1/λ

mfp

,whereσ

tot

is the to-

tal collision cross section and λ

mfp

the mean free path

between collisions, and M

= S, the stopping power.

and M

give the width and skewness of F(∆).

Higher moments are not very useful [91.53] except

for special applications [91.54–56]. For incident elec-

trons, a further averaging of energy loss over different

paths must be performed because of multiple angular

scattering.

91.3.1 Total Collision Cross Section M

A simple result for M

is obtained with the Rutherford

cross section

= NZ



(E) dE

= NZ



min

−

max



(91.16)

Clearly,

is very sensitive to the choice of E

min

and there is no simple prescription for choosing it, as

is evident from Fig. 91.3. The same applies to the bi-

nary encounter approximation [91.32]. From the Bethe

model, a good relativistic approximation to M

is given

by [91.27, 28, 57]

= NZ



lnβ

−β

+11.227



= NZ

τ(β) . (91.17)

Val ue s for g

and h

may be found in [91.57]. For

Si, He, Ar, ethane, and butane, values of τ

, cal-

culated by numerical integration of σ(E) obtained

with the FVP method, are given in Table 91.1.

For Si, comparison values calculated with the Bethe

model are also given. The quantity τ(β) is more

suitable for interpolation than M

. An extensive de-

scription of cross sections are given for liquid water

in [91.58].

Part G 91.3

Charged-Particle–Matter Interactions 91.3 Moments of the Cross Section 1379

91.3.2 Stopping Power M

The stopping power is usually written in the form

= S = NZ

2B , (91.18)

where B is called the stopping number. M

calculated

with the Rutherford cross section is

= NZ

max



Eσ

(E) dE = NZ

max

(91.19)

To obtain realistic values, it is evident from Fig. 91.3 that

asmallvaluemustbechosenforE

to compensate for

the peaks in σ(E). Note that for most applications in high

energy physics (e.g. Time Projection Chambers [91.59,

60]) M

is not useful [91.4].

The Bethe Model

In the Bethe model of stopping powers, dσ(E, K)

from (91.13) must be integrated over both E and

Q =

/2m [91.37,38]. Since f(E, K) is nearly con-

stant near K = 0 [91.61](Fig.91.4), the integral may be

broken into four parts according to

S =

N k







f(E, 0)

∞



f(E, K)



[ f(E, K) − f(E, 0)]

−



[ f(E, K) − f(E, 0)]



(91.20)

where Q

≈ E

/2mv

[91.27, 28], and Q

is cho-

sensuchthat f(E, K) differs little from f(E, 0) in

the interval 0 ≤ K ≤

√

2mQ

/ [91.36, 62]. Collisions

with Q < Q

are “distant” and those with Q > Q

are

“close”. The integrals simplify by interchanging the or-

der of integration in the second and third terms, and by

using the sum rule [91.27, 28, 34]

∞



f(E, K) dE = Z

, (91.21)

for all K. The last term of (91.20) is then small and the

second last vanishes exactly. The remaining two terms

give

S =



2mv



+ln

max



(91.22)

where  is the logarithmic mean excitation energy de-

ﬁned by

ln =



f(E) ln E dE , (91.23)

and Q

max

= 2m

is the maximum energy loss



for electrons, Q

max

[91.3]



. Including

relativistic and other correction terms, the ﬁnal result

for M

 m

S =

N Z



−

C(β)

+ Z

(β) +Z

(β)

[G(M

,β)−δ(β)]



, (91.24)

where

= ln

2mc



−β

(91.25)

is the uncorrected stopping number. In the limit β → 0,

reduces to the terms in brackets in (91.22). The

other correction terms are as follows [91.31].

The Shell Correction. C(β) accounts for the last term in

(91.20), together with modiﬁcations of dσ(E, Q) near

Q = E

max

[91.3]. It can be estimated on a shell-by-

shell basis [91.63–66] using nonrelativistic hydrogenic

calculations for the K- and L-shells [91.35, 37, 38],

and rescaling methods for the outer shells which have

not been calculated directly [91.63, 64, 67]. The ef-

fects are important for small β, but simple formulas

are not known. A calculation for Al and Si based on

a model more realistic than the hydrogenic one is given

in [91.68].

The Barkas Term. L

(β) arises from polarization of the

target electrons by the incident particle [91.69,70]. Var-

ious approximating functions and ﬁts to experimental

data are described in [91.71].

The Bloch Term. L

(β) arises from corrections to the

approximation that for close collisions, the electrons

can be represented by plane waves [91.72]. Conﬁne-

ment of the electrons to the interior of a cylinder of

atomic dimensions introduces transverse momentum

components, resulting in the widely used correction

(β) =−q

∞



j=1







(91.26)

Part G 91.3

1380 Part G Applications

with y = Z

α/β.Fory =0, the sum is ζ(3)  1.202 057.

A new approach can be found in [91.73, 74]. The need

for the L

and L

terms was established experimen-

tally in [91.75], and discussed in a more general context

in [91.76].

The Mott Term. G(M

,β) is a kinematic recoil correc-

tion which becomes important for relativistic projectiles.

In the limit of a point-like spinless nucleus, the correc-

tion is

G(M

,β)=−ln(1 +2t) −tβ

/γ

, (91.27)

where t = mγ/M

[91.29]. The correction is negligible

for γ<100 and M

> m

The Density Correction. δ(β) arises from the dielectric

response of a solid absorber as a whole to the electric

ﬁeld of the projectile, and the work done by the inter-

action [91.3, 29]. Sternheimer’s algorithm [91.77, 78]is

usually used, as summarized in [91.29].

The remaining parameter to be discussed in (91.24)

is . If the oscillator strength distribution f(E) is known,

then  can be calculated directly from (91.23). Results

for many gases are given in [91.45]. The values give good

agreement with experimental stopping powers [91.79].

For solids, the deﬁnition [91.3]

ln =

π( ω

)

∞



E Im



−1

(E)



ln E dE

(91.28)

may be used, where ω

is the plasma energy for all

the electrons, deﬁned by (

)

= 830.4 Z/A with

in eV. For metals, this is substantially larger than

the plasmon energy associated with the conduction

electrons. Only for Al [91.80] and for water [91.81]

have sufﬁciently good measurements of Im[−1/(E)]

been available to permit the use of this method. For

other materials,  can be deduced from measurements

of S, provided that the other corrections in (91.24)are

known sufﬁciently well. A list of values for all elem-

ents and many compounds is given in [91.66]. See

also [91.25, 63–65, 79, 82–87].

For rough estimates of , the approximation [91.88]

≈







11.7 +11.2/Z

eV , Z

≤ 13

9.5 ±1eV , Z

> 13

(91.29)

is useful, together with the Bragg rule

ln =



ln 

(91.30)

for compounds and composite materials, where n

is the

electron density associated with element i.However,

chemical shifts may be as large as 10% [91.89].

The Fermi Virtual Photon Method

From (91.14), the nonrelativistic FVP approximation to

the stopping number B(β) is

B(β) =







max



min



f(E



) dE



. (91.31)

Although the integrals must now be calculated numer-

ically, the full f(E, K) is not required, and in the case

of silicon, the results are in close agreement with the

corresponding Bethe model.

Stopping Power at Small Speeds

For small speeds, the various correction terms in the

stopping number B,(91.24), become large compared

with B

[91.63, 64, 68]. In particular, for 2mv

=, B

becomes zero. For example, for α-particles in U (=

840 eV), B

= 0atT = 1.5MeV, and B then consists

only of correction terms. For smaller energies, empirical

approaches are used to describe S. Many of the tables

referenced above give such data.

Mean Energy Loss per Collision

The quantity E=M

is the mean energy

loss per collision. For substances with Z < 20,

E∼50–100 eV. It changes at most by a factor of 1.5

for βγ > 0.1. In order to choose a suitable method for

calculating straggling functions, it is useful to estimate

the number of collisions in a thickness x of absorber.

For less than 2000 collisions, the convolution method of

Sect. 91.4.2 should be used (Fig. 15 in [91.5]).

91.3.3 Second Moment M

The relativistic result calculated with the Rutherford

cross section is

= NZ



1 −β



max

(91.32)

= 2NZ

1 −β

= 0.156 915

1 −β

MeV

/g .

For small β,

is practically independent of β.

A better approximation can be achieved with the binary

Part G 91.3

Charged-Particle–Matter Interactions 91.4 Energy Loss Straggling 1381

encounter method:

= NZ

max



1 −



max



max

min

−β



(91.33)

where the summation extends over atomic shells l.For

min

the ionization energy J

for shell l can be used,

while U

represents the kinetic energy of the electrons

in shell l. This approximation is only useful for rela-

tively large x [91.5]. By using sum rules, Fano [91.3,

(72)] achieved a better approximation, which corres-

ponds to the Bethe approximation for the stopping power

[91.5, 90]. Hydrogenic values of M

are calculated

in [91.53].

91.4 Energy Loss Straggling

91.4.1 Straggling Parameters

Parameters for Thick Absorbers

Straggling is due to the stochastic nature of the en-

ergy losses of the charged particles. Because the single

collision spectrum is highly skewed (the most proba-

ble energy loss is ≈ 20 eV, the mean value ≈ 100 eV),

straggling functions will also be skewed. Four param-

eters are useful in a preliminary study of straggling

problems [91.47]. The parameter

ξ = NZ

x = 153.537

x keV cm

(91.34)

gives the energy loss [calculated with σ

(E)]which,

on the average, is exceeded once for each particle in

its passage through an absorber of thickness x,i.e.,for

ξ  E

max

xNZ

max



(E) dE = 1 . (91.35)

The parameter κ = ξ/E

max

is related to the skewness

of the straggling function: γ

= 1/4κ. The mean energy

loss is

∆=xM

= 2ξ2B = 2κE

max

B , (91.36)

and the standard deviation of F(∆) is

= xM

∼ xNZ

max

= ξE

max

= κE

max

(91.37)

For thick absorbers, the straggling function becomes

approximately Gaussian [91.5, 24]. The requirement for

this to occur is γ

→ 0, thus κ →∞,also∆→∞,

and x →∞.

Parameters for Thin Absorbers

The parameters described above are not suitable for de-

scribing F(∆) for very thin absorbers. Instead, ∆

and

Γ are used. Values for pions traversing Ar are given as

a function of thickness x in Tables 91.2, 91.3.However,

before comparing with experimental data, values of ∆

must be converted into ionization values, and the detec-

tor and ampliﬁer noise must be added [91.5] (Sect. 91.7).

Landau [91.6] gave an expression for the most proba-

ble energy loss as a function of particle speed. It was

modiﬁed in [91.5]to

∆

= ξ



2mc

+ln

+0.200 −β

−δ



(91.38)

Table 91.2 Calculated most probable energy loss ∆

of pions with Z

=±1 and kinetic energy T passing

through a distance x of argon gas



at 760 Torr, 293 K,

 = 1.66 g/dm



. For heavy ions (α,C

), the values scale

as Z

1.3

(for a better approximation, see Table V in [91.5]).

Units of ∆

are keV. The quotient ∆

/x increases with x

x(cm)

T (MeV) 0.5 1 2 4 8

1 29.373 63.341 130.662 265.062 533.811

3 9.820 21.598 47.000 101.329 216.013

10 3.104 6.842 14.950 32.558 69.966

30 1.153 2.687 5.927 12.883 28.023

100 0.376 1.274 2.928 6.412 13.884

300 0.288 0.973 2.313 5.099 10.993

1×10

0.303 1.042 2.445 5.356 11.494

3×10

0.344 1.217 2.783 6.044 12.926

1×10

0.384 1.390 3.145 6.784 14.495

3×10

0.653 1.515 3.405 7.322 15.663

1×10

0.667 1.605 3.595 7.725 16.575

Part G 91.4

1382 Part G Applications

Table 91.3 Calculated values of Γ (fwhm) of the straggling

function F(∆) (see Table 91.2). As a rough approximation,

Γ ∼ x

0.8

(Table VI in [91.5])

x(cm)

T (MeV) 0.5 1 2 4 8

1 16.014 24.961 35.503 51.327 69.120

3 6.283 12.012 22.928 43.393 68.589

10 2.507 4.563 8.659 16.153 30.026

30 1.360 2.279 3.922 7.441 13.881

100 0.781 1.434 2.350 4.178 7.705

300 0.574 1.239 2.030 3.410 6.232

1×10

0.621 1.286 2.085 3.397 6.340

3×10

0.752 1.391 2.244 3.687 6.844

1×10

0.905 1.510 2.432 3.999 7.502

3×10

0.983 1.615 2.548 4.314 7.956

1×10

1.040 1.701 2.689 4.666 8.399

1.8

1.6

1.4

1.2

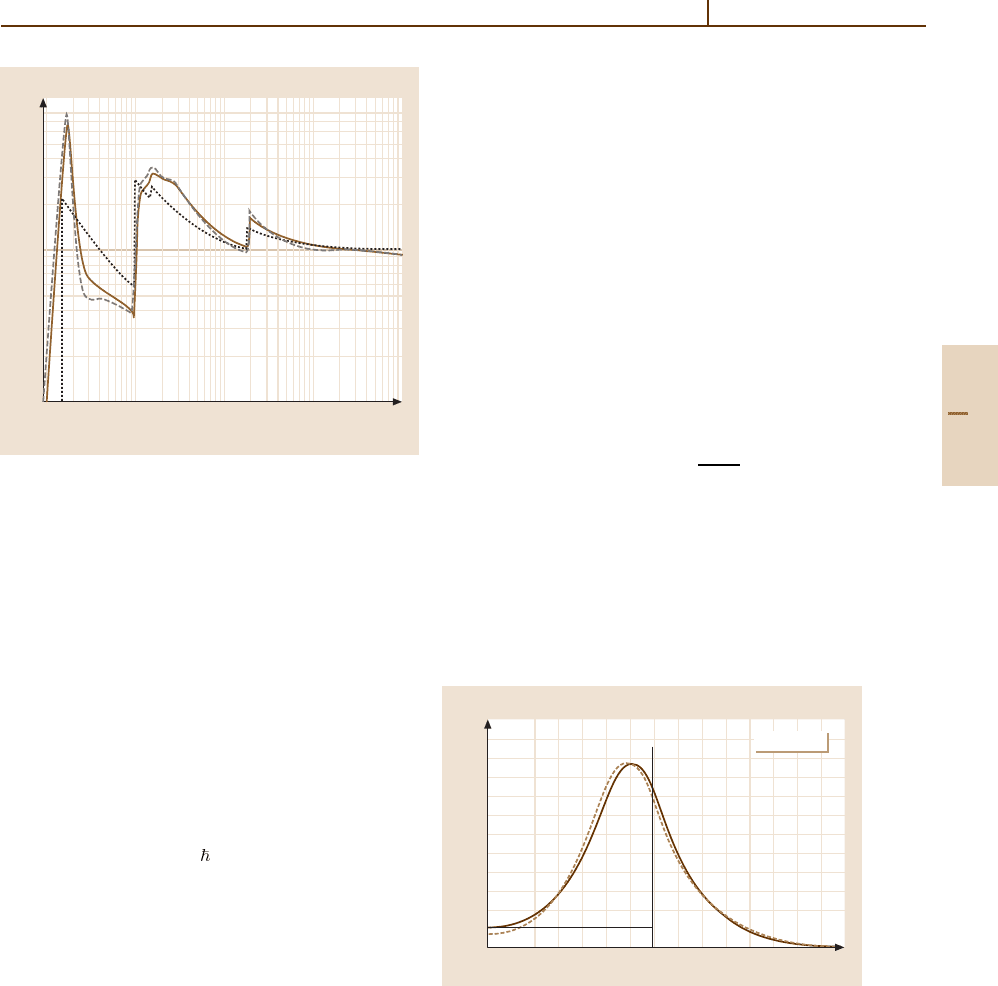
1.0

1 5 10 50 100 500 1000

scaled ∆

80 cm

30 cm

4 cm

2 cm

1 cm

βγ

BBx = 1, 2, 4, 30, 80 cm Ar

Fig. 91.5 The dependence of most probable energy-loss

values ∆

(βγ ; x)/x > for segments of length x. Solid

line BB: the Bethe–Bloch function dE/dx(βγ) [91.4].

Other lines are for the segment lengths x marked at right.

The functions are scaled with a factor g(x) such that they

concide at minimum ionization

More accurate functions ∆

are obtained with the

collision spectra of Fig. 91.3, and are called Bich-

sel functions [91.59]. For sufﬁciently large ξ, ∆

and ∆

agree within a few %. Examples are shown in

Fig. 91.5, and for comparison the Bethe-Bloch function

dE/ dx [91.4]isgiven.

Parameters for Extremely Thin Absorbers

If the number n

of collisions in the absorber is less than

about 16, F(∆) still shows the details of σ(E) (Fig. 91.6).

0.04

0.02

10 100 1000

0.03

0.02

0.01

10 100 1000

0.01

0.005

10 100 1000

0.002

0.001

10 100 1000

F(∆)d ∆

∆(eV)

F(∆)d ∆

∆(eV)

F(∆)d ∆

∆(eV)

F(∆)d ∆

∆(eV)

∆

<∆>

= 1

x = 0.26 µm

= 37%

∆

<∆>

= 2

x = 0.52 µm

= 14%

∆

<∆>

= 4

x = 1.04 µm

= 1.8%

<∆>

∆

= 8

x = 2.1 µm

Fig. 91.6 Calculated straggling functions F(∆) for 1 GeV

pions traversing four thicknesses x of silicon. The aver-

age number of collisions is n

, with E=106 eV, the

mean energy loss is ∆=n

E, shown by an arrow.

The number of particles traversing the absorber without

a collision is n

. The peak heights do not follow a Poisson

distribution because successive convolutions give a broader

distribution. The Landau function [91.6]forn

= 4is

shown by the broken line. For all, the most probable en-

ergy loss calculated according to Landau, ∆

(91.38), is

shown

The most probable energy losses are much less than ∆.

Functions of this type have been observed with electron

microscopes [91.10]. For comparison, the Landau strag-

gling function [91.6] is also shown. This result, derived

from σ

(E), does not show the structure of a realistic

spectrum.

Detector noise and energy loss to ionization conver-

sions introduce important changes [91.91–94]tothe

energy loss spectrum. In particular, if n

< 4, a large

Part G 91.4