Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

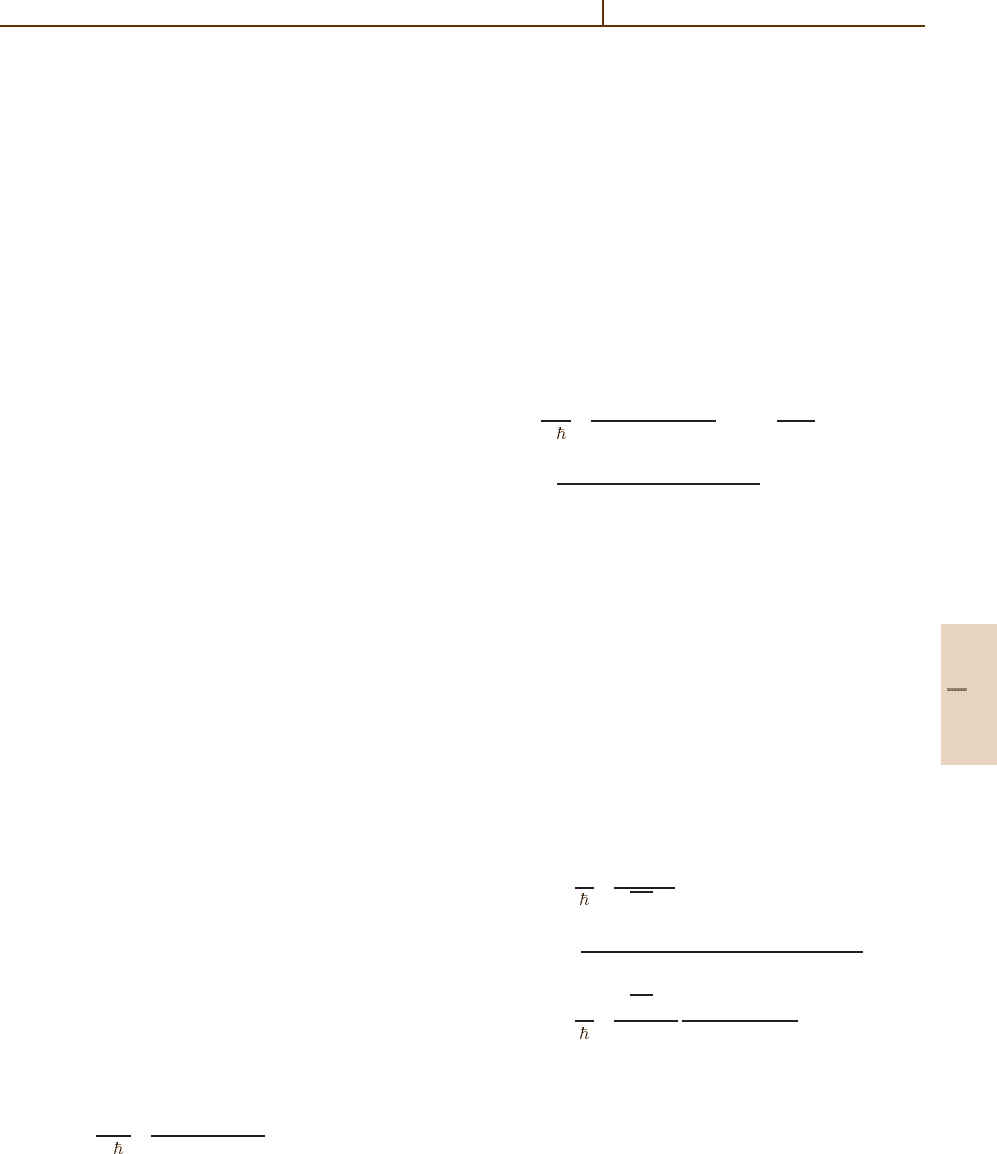
Absorption and Gain Spectra 69.5 Two-Level Doppler-Free Spectroscopy 1015

unity with a positive slope. This is called anomalous

dispersion and signiﬁes the presence of a gain proﬁle.

In such a medium, α



=Im[α(ω)]is of opposite sign, as

seen from (69.47); in the inverted medium, α



becomes

negative near ∆ = 0. From (69.2), this indicates a grow-

ing electromagnetic ﬁeld, i. e., an amplifying medium.

The amplitude grows, and the assumption of a small

signal becomes invalid. Then saturation has to be in-

cluded, either at the rate equation level or by performing

a full density matrix calculation. This regime describes

a laser with saturated gain. In steady state, the two lev-

els become nearly equally populated (ρ

≈ρ

), and the

operation is stable. The theory of the laser is discussed

in detail in Chapt. 70.

69.5 Two-Level Doppler-Free Spectroscopy

The linear absorption of a scanned laser signal

deﬁnes linear spectroscopy and gives information char-

acterizing the sample. However, Sect. 69.3 shows that

inhomogeneous broadening masks the desired informa-

tion by dominating the line shape. The availability of

laser sources has made it possible to overcome this limi-

tation, and to use the saturation properties of the medium

to perform nonlinear spectroscopy. This section dis-

cusses how Doppler broadening can be eliminated to

achieve Doppler-free spectroscopy. Similar techniques

may be used to overcome other types of inhomogeneous

line broadening; a general name is then hole-burning

spectroscopy (see the discussion in Sect. 69.3). Other

aspects of nonlinear matter-light interaction are found

in Chapt. 72.

Equation (69.24) shows that a single laser cannot re-

solve beyond the Doppler width. However, if a strong

laser is used to pump the transition, a weak probe

signal can see the hole burned into the spectral pro-

ﬁle by the pump. This technique is called pump-probe

spectroscopy. Because the probe is taken to be weak,

perturbation theory may be used to calculate the in-

duced polarization to lowest order in the probe amplitude

only.

In the ﬁeld expansion (69.31), deﬁne the strong

pump amplitude to be E

and the weak probe E

frequency ω

. From the resolution (69.34), the com-

ponent ρ

(2)

carries the information about the linear

response at frequency ω

.IftheﬁeldE

propagates in

a direction opposite to that of E

, its detuning is

∆



= ∆

−kv (69.49)

(as compared with ∆



=∆

+kv for E

). Since ω

ω

the two k-vectors are nearly equal in magnitude.

The linear response now becomes

(2)



idE



γ +i(∆

−kv)



−ρ



(69.50)

With only the signal E

present, the population differ-

ence follows directly from (69.22)). The linear response

at frequency ω

is then

(2)





iγ +

(

∆

−kv

)

+(∆

−kv)



1 −

Ω



(∆

+kv)

+γ

+Ω

γ/Γ



(69.51)

This is the linear response of atoms moving with vel-

ocity v. To obtain the polarization of the whole sample,

we must average over the velocity distribution using the

Gaussian weight (69.20). The ﬁrst term in (69.51)gives

the linear response in the form of a Voigt proﬁle,as

discussed in Sect. 69.3. This part of the response carries

no Doppler-free information. The second terms contain

the nonlinear response. This shows the details of the

homogeneous features under the Doppler line shape.

For simplicity we assume the Doppler limit, γ  ku ,

and neglect the variation of the Gaussian over the atomic

line shape. We also neglect the power broadening due

to the ﬁeld E

and obtain, using (69.13), (69.20), and

(69.51),



(ω) =−





Ω

√

2πΓu

+∞



−∞



(

∆

−kv

)

+γ



(

∆

+kv

)

+γ



=−





√

2πΩ

4Γku

(ω −ω

)

+γ

(69.52)

This denotes the energy absorbed from the ﬁeld E

,as

induced nonlinearly by the intensity E

. The resonance

is still at ω = ω

, but with a homogeneous atomic line

shape. In the Doppler limit, the Doppler broadening is

Part F 69.5

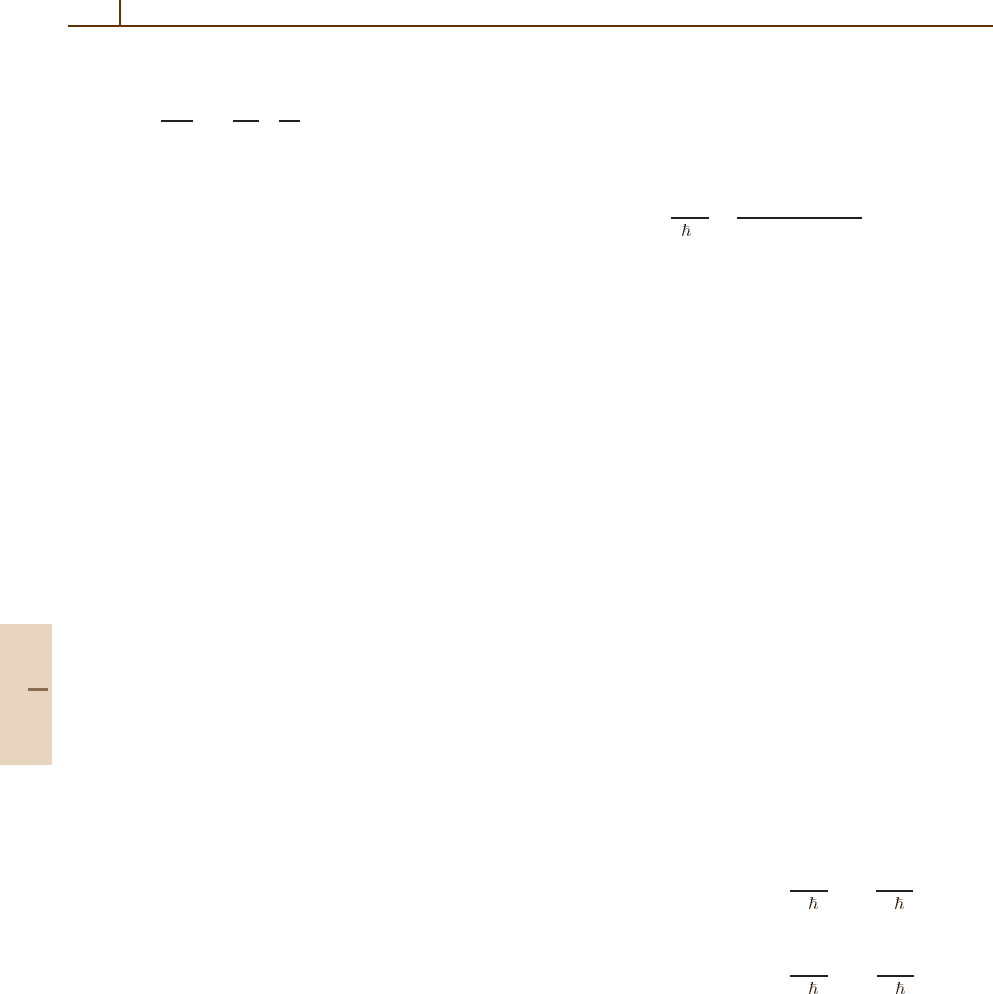
1016 Part F Quantum Optics

only seen in the prefactor

Ω

Γku



Ω

Γγ



(69.53)

which shows that only the fraction (γ/ku ) of all atoms

can contribute to the resonant response. The ﬁrst factor

on the right-hand side of (69.53) is the dimensionless

saturation factor.

The Doppler-free character of this spectroscopy de-

rives from the fact that the two ﬁelds burn their two

separate Bennett holes at the v elocities

=−∆

, and kv

= ∆

. (69.54)

When these two groups coincide, i. e., when v

= v

the probe E

sees the absorption saturated by the pump

ﬁeld E

and a decreased absorption is observed. For

= ω

, the two holes meet in the middle at zero ve-

locity. With two different frequencies, one can make

the holes meet at a nonzero velocity to one side of the

Doppler proﬁle. The decreased absorption seen in these

experiments is called an inverted Lamb dip Chapt. 70.

The results derived here are based on a simpliﬁed

view of the pump-probe response which in turn is based

on the rate equation approach. Certain coherent effects

are neglected, which would considerably complicate the

treatment [69.2]. Section 69.6 discusses these effects in

the three-level system where they are more important.

In addition to measuring the probe absorption in-

duced by the pump ﬁeld, it is also possible to observe

the dispersion of the probe signal caused by the satu-

ration induced by the pump. Assuming that the pump

introduces the velocity dependent population difference

−ρ

= ∆ρ(v) , (69.55)

then from (69.50), Re(n) is



= 1 +

2 ε



∆

−kv

(∆

−kv)

+γ

∆ρ(v)dv.

(69.56)

From (69.2), the phase of the electromagnetic signal

feels the value of n



through the factor

E ∝ exp(iωn



z/c). (69.57)

Thus, by modifying ∆ρ(v), a pump laser can control

the phase acquired by light traversing the sample, and

thereby control the optical length of the sample.

A real atom has magnetic sublevels, which are

coupled to light in accordance with dipole selection rules

(see the discussion in Chapt. 33). If a pump laser is used

to affect populations in the various sub-levels differ-

ently, the optical paths experienced by the differently

circularly polarized components of a linearly polarized

probe signal are different. Thus, its plane of polariza-

tion will turn, corresponding to the Faraday effect.By

tuning the pump and the probe over the spectral lines

of the sample, the turning of the probe polarization pro-

vides a signal to investigate the atomic level structure.

This method of polarization spectroscopy can be used

both with two-level and three-level systems [69.7].

69.6 Three-Level Spectroscopy

New nonlinear phenomena appear when one of the

levels in the two-state conﬁguration, |e say, is cou-

pled to a ﬁnal level | f  by a weak probe. This may

be above the level |e (the cascade conﬁguration de-

noted by Ξ)orbelow|e (the lambda conﬁguration Λ)

(if the third level were coupled to |g we would talk

about the inverted lambda or V conﬁguration) [69.8].

For simplicity, only the Ξ conﬁguration is discussed

here.

Assume that the level pair |g↔|e is pumped by

the ﬁeld E

and its effect probed by the ﬁeld E

coupling

|e↔|f . The dipole matrix element is d

=f |H|e.

The RW A is now achieved by introducing slowly varying

quantities through the deﬁnitions

= e

i(k

z−ω

= e

(

)

z−

(

+ω

)

, (69.58)

and omitting all components oscillating at multiples of

the optical frequencies. From the equation of motion for

the density matrix, the steady state equations are [69.2]

(∆

v −iγ

)

−

[(∆

+∆

) +(k

)v −iγ

]

−

(69.59)

where the second step detuning is now

∆

= ω

−ω

. (69.60)

These equations contain the lowest order response

proportional to E

, including some coherence effects.

The coherence effects remain to lowest order, even when

the last term in (69.59) is neglected; in that case, the

Part F 69.6

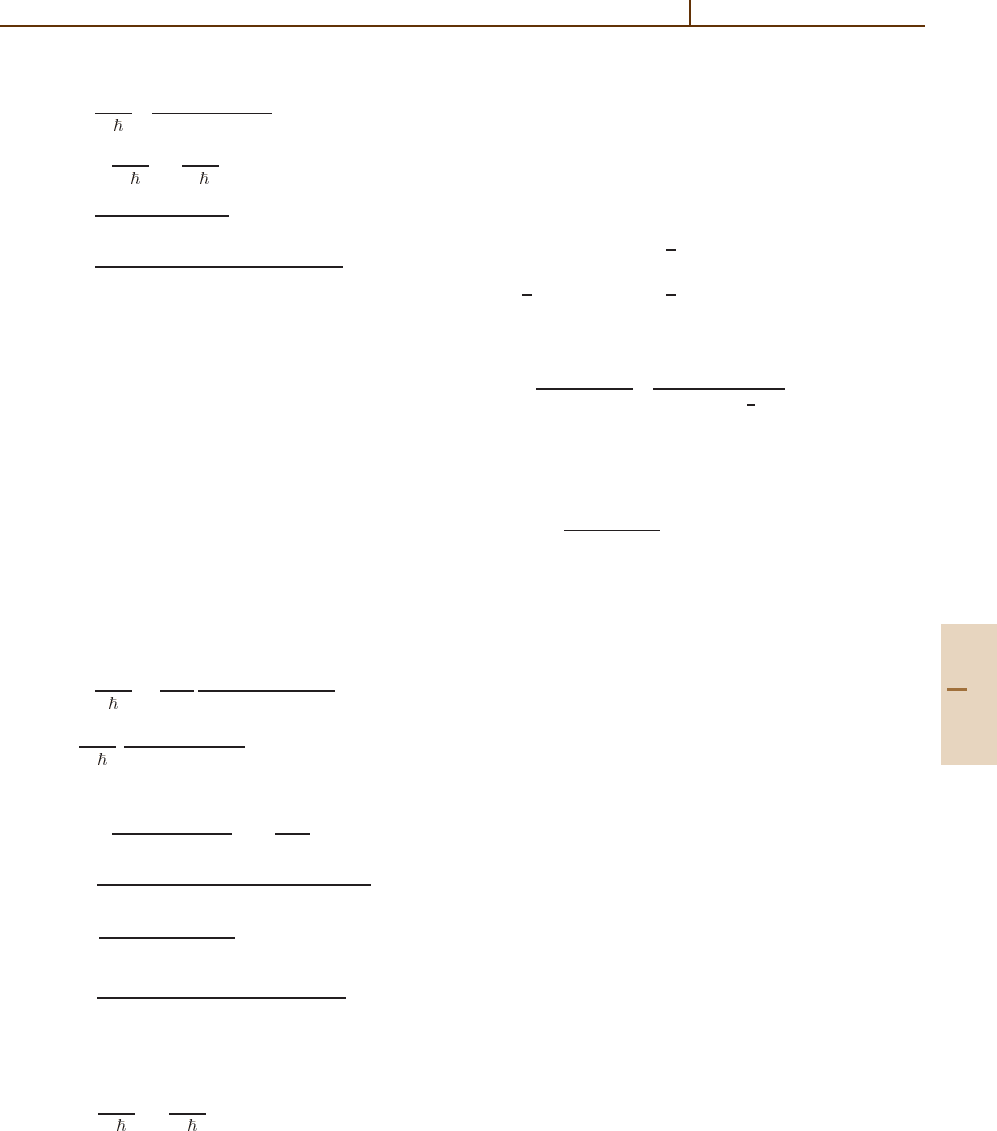
Absorption and Gain Spectra 69.6 Three-Level Spectroscopy 1017

solution is





∆

v −iγ

−







(∆

v −iγ

)



(

∆

+∆

)

(

)

v −iγ



(69.61)

The result to lowest order in E

follows by replacing

the density matrix elements for the two-level system

|e↔|g by their results calculated without this ﬁeld.

This shows that the polarization induced at the fre-

quency ω

consists of two parts: one induced by the

population excited to level |e by the ﬁeld E

pro-

portional to ρ

, and the other one is induced by the

coherence

created by the pump. Retaining only the

former produces a rate equation approximation, called

a two-step process. This misses important physical fea-

tures which are included in the second term called

a two-photon or coherent process.

In order to see the effects of the two terms

most clearly, consider the two-level matrix elements

from (69.11)and(69.12) in lowest perturbative order

with respect to the pump ﬁeld E

,i.e.,





2γ

(

∆

)

+γ

∆

v −iγ

(69.62)

From (69.61), these matrix elements give

=−



∆

v −iγ



2γ





∆

v +iγ



∆

v −iγ



−



∆

v −iγ





(

∆

+∆

)

(

)

v −iγ





(69.63)

where

A =−







. (69.64)

The imaginary part of this yields the absorptive part

of the polarization at the frequency ω

.Theﬁrstterm

becomes the product of two Lorentzians, and is an

incoherent rate contribution. It dominates when the in-

duced population ρ

decays much more slowly than the

induced coherence

,i.e.,whenγ

 γ

The signiﬁcance of the second term in (69.63)is

evident in the limit when no phase perturbing processes

intervene, so that

= Γ, γ

Γ,

,γ

(γ

+Γ). (69.65)

For v =0,

becomes

=−

∆

+(Γ/2)



∆

+∆

−i



(69.66)

Neglecting the decay of the ﬁnal level | f , γ

→0, the

absorption becomes proportional to





π|A|

∆

(

Γ/2

)

(

∆

+∆

)

(69.67)

In this limit, strict energy conservation between the

ground state and the ﬁnal state must prevail; the ﬁnal

state must be reached by the absorption of exactly two

quanta. The delta function in (69.67) indicates precisely

this:

∆

+∆

= ω

+ω

−

(

+ω

)

= ω

−ω

= 0 . (69.68)

The detuning and the width of the intermediate state

affect the total transition rate, but not the condition of

energy conservation. The presence of the second term

in (69.63) makes the resonance contributions at

∆

= ω

−ω

= 0 (69.69)

cancel approximately. Only a two-photon transition re-

mains; in the Λ conﬁguration this would be a Raman

process (Chapts 62 and 72).

If the velocity dependence in (69.63) is retained, the

nonlinear response of an atomic sample must be aver-

aged over the velocity distribution given by the Gaussian

(69.20). The computations become involved, but the re-

sults show more or less well resolved resonances around

the t wo positions (69.68)and(69.69), i. e., the coher-

ent two-photon process and the single step rate process

|e→|f appearing due to a previous single step process

|g→|e;thisisthetwo-step process.

Part F 69.6

1018 Part F Quantum Optics

A special situation arises when the intermediate

step is detuned so much that no velocity group is in

resonance, i. e., |∆

|≈|∆

|kv for all velocities con-

tributing signiﬁcantly to the spectrum. Then the second

coherent term of (69.63) can be written in the form

=−

∆



(

∆

+∆

)

(

)

v −iγ



(69.70)

If the two ﬁelds E

and E

have the same frequency but

are counterpropagating, then k

= 0, and no vel-

ocity dependence occurs in (69.70) for the two-photon

resonance. All atoms in the sample contribute to the

strength of the resonance, and then polarization is ob-

tained directly by multiplication with the total atomic

density. Equation (69.13)thengives





2 ∆





2ω −ω



+γ

. (69.71)

This is a sharp Doppler-free resonance on the two-

photon transition ω

. The advantage is that all atoms

contribute with the sharp line width γ

, which is not

easily affected by phase perturbations because of the

two-photon nature of the transition. The disadvantage is

the weakness of the transition, which is caused by the

large detuning, making d

/|∆

|1 in most cases.

With tunable lasers, however, this Doppler-free spec-

troscopy method has been used successfully in many

cases.

69.7 Special Effects in Three-Level Systems

We continue our considerations of a three-level sys-

tem but this time in the V -conﬁguration. Thus, we have

a ground state |g coupled to a doublet of excited states

{

|e, | f 

}

through the interaction

V = Ω

|ge|+Ω

|g f |+h.c. , (69.72)

where the couplings are due to radiation ﬁelds and given

Ω

. (69.73)

We use the rotating wave approximation and set the

detunings to

∆ω

= ω

−ω

and ∆ω

= ω

−ω

, (69.74)

where the frequency ω

derives from the coupling

ﬁeld E

. The energy E

= 0.

The time-dependent Schrödinger equation for this

system is then written as

= Ω

+Ω

, (69.75)

= ∆ω

+Ω

, (69.76)

= ∆ω

+Ω

. (69.77)

We now introduce the two new variables

Ω

−1



Ω

+Ω



(69.78)

Ω

−1



Ω

−Ω



(69.79)

where

Ω

= Ω

+Ω

. (69.80)

The equations of motion follow:



Ω

∆ω

−

Ω

∆ω



Ω



Ω



∆ω

−∆ω





∆ω

Ω

+∆ω

Ω





(69.81)



Ω

∆ω

Ω

∆ω



Ωc

Ω



∆ω

Ω

+∆ω

Ω



+Ω

Ω



∆ω

−∆ω





Ωc

(69.82)

We notice that c

is not coupled to the ground state,

but, in general, its coupling to the state c

provides an

indirect coupling. This indirect coupling, however, can

be made to disappear, if we set ∆ω

=∆ω

≡∆ω.Then

we ﬁnd the equations

= ∆ωc

Ωc

. (69.83)

This describes a pair of coupled quantum levels and

a single uncoupled level. Thus, if we start in the ground

state, this latter level can never be populated. It re-

mains unpopulated and is called a dark state. This state

Part F 69.7

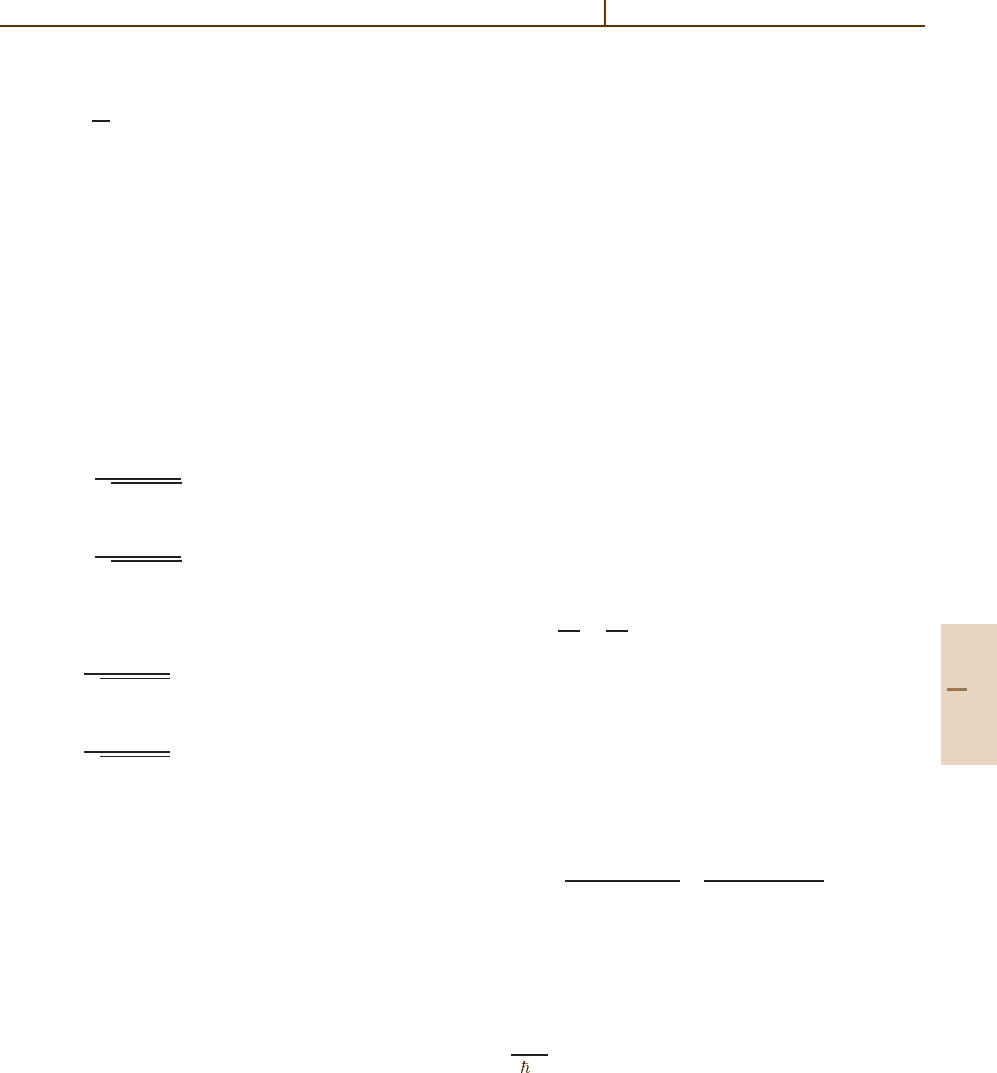
Absorption and Gain Spectra 69.7 Special Effects in Three-Level Systems 1019

corresponds to the superposition

|NC=

Ω

(

Ω

|e−Ω

| f 

)

. (69.84)

Using the coupling operator (69.72), we ﬁnd the matrix

element

g|V |NC=0 .

(69.85)

We also notice that the dark state can be found if the

states |e and | f  are the lower ones, i. e., we have the

Λ-conﬁguration.

Alternatively, if we start the system off in the dark

state, it will never be able to get out of this state. This

is also taken to hold true if we let the couplings depend

slowly on time. In this case, we may let Ω

come on

later than Ω

. Then we may have

lim

t→−∞





Ω



Ω

+Ω





= 0 ,

lim

t→−∞





Ω



Ω

+Ω





= 1

(69.86)

and

lim

t→∞





Ω



Ω

+Ω





= 1 ,

lim

t→∞





Ω



Ω

+Ω





= 0 .

(69.87)

Both couplings are thus pulses, but they occur with

a slight time delay. If we now start the system in the

state |e, we ﬁnd from (69.84)that

lim

t→−∞

|NC=|e , (69.88)

and

lim

t→+∞

|NC=−|f  . (69.89)

Thus, by keeping the system in this uncoupled state

we can adiabatically transfer its population beteen the

states without involving any population of the interme-

diate state |g. Especially if this is an upper state, which

may decay and dephase rapidly, the proposed popula-

tion transfer may be greatly advantageous. Because it

is usually applied in the Λ-conﬁguration, it is termed

Stimulated Raman Adiabatic Passage (STIRAP).

The dark state has found a wide range of applications

in laser physics. As we may use the method to pass ra-

diation through a medium without any absorption, it has

led to the phenomenon of light-induced transparency. It

can also be used to affect the index of refraction with-

out having the accompanying absorption. The absorptive

part of a resonance normally manifests itself as a quan-

tum noise; utilizing the dark state idea one may reduce

the noise in quantum devices. The dressing of the lev-

els due to the special features of the interaction has also

made it possible to achieve lasing without an inversion

of the bare levels. These topics, however, will not be

treated here.

A special application of the method to affect the

refractive index deserves a more detailed consideration.

We look at the relationship between the electric ﬁeld

vectors in the medium:

D(ω) = ε

E + Nα(ω)E(ω) = χ(ω)ε

E(ω) ,

(69.90)

where χ(ω) is the susceptibility of the medium. From

Maxwell’s equations we ﬁnd the relation (68.24)

= n

(ω)

[

1 +χ(ω)

]

(69.91)

If we take the real parts of the quantities, this describes

the propagation of waves in the medium.

Now we may use the relations (69.16) to estimate the

function α(ω) in the case when we have two weak ﬁelds

exciting the three-level system in the V -conﬁguration.

We assume that both couplings have the same frequency,

= ω

= ω. We write

χ(ω) ≈ Λ



(

ω −ω

)

(

ω −ω

)

+γ



ω −ω





ω −ω



+γ



;

(69.92)

in the weak ﬁeld limit we may assume the two processes

to add independently. The parameter

Λ =

2 ε

(69.93)

has the dimension of a frequency and indicates the

strength of the interaction. It is clear that tuning the

frequency between the levels may give rise to a value

of zero for the susceptibility. For a large enough γ ,we

Part F 69.7

1020 Part F Quantum Optics

write, in the neighbourhood of the zero,

χ(ω) ≈

2Λ



ω −



(69.94)

where

ω =

(ω

+ω

We now have the relation (69.91) to determine

the dispersion relation, and assuming the effect of the

medium to be substantial, we may derive an expression

for the group velocity in the medium

−1

∂k

∂ω

(69.95)

We ﬁnd

2ω

(

1 +χ

)



2Λ



(69.96)

Even though χ =0 near the point

ω, we still have ω ∼ck,

so that

1 +

Λω

≈ c



Λω



 c .

(69.97)

The last inequality follows from the fact that in all cases

γ  ω.

We have thus found that utilizing the interference of

two near quantum levels, the refractive index may ac-

quire a very strong dependence on frequency. This may

manifest itself in an exceedingly slow propagation of

light pulses. Such slow light has been shown to travel

at only a few kilometers per hour, which is a most re-

markable result. The drawback is, however, that this can

only occur over a very narrow frequency range, as fol-

lows from the assumption of a strong dependence on

frequency.

69.8 Summary of the Literature

Much of the material needed to formulate the basic

theory of interaction between light and matter can be

found in the text book [69.2]. A comparison between

the harmonic model and the two-level model is given by

Feld [69.1]. The density matrix formulation is presented

in detail in [69.2]. The inﬂuence of various line broad-

ening mechanisms on laser spectroscopy is discussed in

the book [69.3]. The Voigt proﬁle is related to the er-

ror function, which is treated in the compilation [69.5].

The numerical evaluation of the Voigt proﬁle is dis-

cussedin[69.4]. Rate equations are commonly used in

laser theory and they are derived for optical pumping

and laser-induced processes in the lectures [69.6]. The

Doppler-free spectroscopy was developed in the 1960s

and 1970s by many authors following the initial discov-

ery of the Benett hole by Bill R. Bennett Jr. and the

Lamb dip by Willis E. Lamb Jr. Much of the pioneering

work can be found in the book [69.3]. The three-level

work has been reviewed by Chebotaev [69.8]. Various

applications of lasers in spectroscopy are treated by Lev-

enson and Kano [69.7]. For references to other topics,

we refer to the specialized chapters of the present book.

Many features of the quantum dynamics of a few-

level system are found in [69.9, 10]. The theoretical

methods to treat such systems are presented in detail

in [69.11]. The ensuing physical processes are presented

in [69.12] with much additional material on quantum

optics phenomena. The basic theory of the dark state

and many of its applications in spectroscopy and laser

physics are found in [69.13]. A rather complete review

of adiabatic processes induced by delayed pulses is the

article [69.14]. The slowing down and stopping of light

is reviewed in [69.15]. A very recent article with earlier

references is [69.16].

References

69.1 M. S. Feld: Frontiers in Laser Spectroscopy,ed.by

R. Balian, S. Haroche, S. Liberman (North-Holland,

Amsterdam 1977) p. 203

69.2 S. Stenholm: Foundations of Laser Spectroscopy

(Wiley, New York 1984)

69.3 V. S. Letokhov, V. P. Chebotaev: Nonlinear Laser

Spectroscopy (Springer, Berlin, Heidelberg 1977)

69.4 W. J. Thompson: Comp. Phys. 7, 627 (1993)

69.5 M. Abramowitz, I. E. Stegun: Handbook of Mathe-

matical Functions (Dover, New York 1970)

69.6 C. Cohen-Tanoudji: Frontiers in Laser Spectroscopy,

ed. by R. Balian, S. Haroche, S. Liberman (North-

Holland, Amsterdam 1977) p. 1

69.7 M. D. Levenson, S. S. Kano: Introduction to Non-

linear Laser Spectroscopy (Academic, New York

1988)

Part F 69

Absorption and Gain Spectra References 1021

69.8 V. P. Chebotaev: High-Resolution Spectroscopy,ed.

by K. Shimoda (Springer-Verlag, Berlin, Heidelberg

1976)

69.9 B. W. Shore: The Theory of Coherent Atomic Excita-

tion: Vol. 1. Simple Atoms and Fields (Wiley, New

York 1990)

69.10 B. W. Shore: The Theory of Coherent Atomic Exci-

tation: Vol. 2. Multilevel Atoms and Incoherence

(Wiley, New York 1990)

69.11 C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg:

Atom-Photon Interactions, Basic Processes and Ap-

plications (Wiley, New York 1992)

69.12 L. Mandel, E. Wolf: Optical Coherence and Quan-

tum Optics (Cambridge Univ. Press, Cambridge

1995)

69.13 M. O. Scully, M. S. Zubairy: Quantum Optics (Cam-

bridge Univ. Press, Cambridge 1997)

69.14 N. V. Vitanov, M. Fleischauer, B. W. Shove,

K. Bergmann: In: Advances of Atomic, Molecular

and Optical Physics, Vol. 46, ed. by B. Bederson,

H. Walther (Academic, New York 2001) p. 55

69.15 A. B. Matsko, O. Kocharovskaya, Y. Restoutsev,

G. R. Welch, A. S. Zibrov, M. O. Scully: Advances in

Atomic, molecular, and Optical Physics, Vol. 46, ed.

by B. Bederson, H. Walther (Academic, New York

2001) p. 191

69.16 M. Bajcsy, A. S. Zibrov, M. D. Lukin: Nature 26,368

(2003)

Part F 69

1023

Laser Principle

70. Laser Principles

Despite their great variety and range of power,

wavelength, and temporal characteristics, all

lasers involve certain basic concepts, such as

gain, threshold, and electromagnetic modes of

oscillation [70.1–3]. In addition to these universal

characteristics are features, such as Gaussian

beam modes, that are important to such a wide

class of devices that they must be included in

any reasonable compendium of important laser

concepts and formulas. We have therefore included

here both generally applicable results as well as

some more speciﬁc but widely applicable ones.

70.1 Gain, Threshold,

and Matter–Field Coupling ...................1023

70.2 Continuous Wave,

Single-Mode Operation ........................1025

70.3 Laser Resonators .................................1028

70.4 Photon Statistics .................................1030

70.5 Multi-Mode and Pulsed Operation ........1031

70.6 Instabilities and Chaos.........................1033

70.7 Recent Developments...........................1033

References ..................................................1034

70.1 Gain, Threshold, and Matter–Field Coupling

All lasers involve some medium that ampliﬁes an elec-

tromagnetic ﬁeld within some band of frequencies. At

the simplest level of description, the amplifying medium

changes the intensity I of a ﬁeld according to the

equation

= gI ,

(70.1)

where z is the coordinate along the direction of propaga-

tion and g is the gain coefﬁcient, typically expressed in

−1

. Ampliﬁcation occurs as a consequence of stimu-

lated emission of radiation from the upper state (or band

of states) of a transition for which a population inversion

exists; i. e., for which an upper state has greater likeli-

hood of occupation than a lower state. Different types of

lasers may be classiﬁed by the pump mechanisms used

to achieve population inversion (Chapt. 71). In the case

that the amplifying transition involves two discrete en-

ergy levels, E

and E

> E

, the gain coefﬁcient at the

frequency ν is given by

g(ν) =

8πn



−



S(ν) .

(70.2)

Here λ = c/ν is the transition wavelength, A



−1



the Einstein A coefﬁcient for spontaneous emission for

the transition, and g

, g

are the degeneracies of the up-

per and lower energy levels. These quantities in nearly

every case are ﬁxed characteristics of the medium, inde-

pendent of the laser intensity or the pump mechanism.

and N

are the population densities



−3



of the

upper and lower levels, respectively, and S(ν) is the nor-

malized transition lineshape function (Chapts. 19 and

69). n is the refractive index at frequency ν of the “back-

ground” host medium and in general has contributions

from all nonlasing transitions. Equation (70.2) describes

either ampliﬁcation or absorption, depending on whether

−(g

is positive (ampliﬁcation) or negative

(absorption).

By far the most common conﬁguration is that in

which the gain medium is contained in a cavity bounded

on two sides by reﬂecting surfaces. The mirrors allow

feedback; i. e., the redirection of the ﬁeld back into the

gain medium for multipass ampliﬁcation and sustained

laser action. The two mirrors allow the ﬁeld to build up

along the directions parallel to the “optical axis” and to

form a pencil-like beam of light. In order to sustain laser

action, the gain in intensity due to stimulated emission

must equal or exceed the loss due to imperfect mirror

reﬂectivities, scattering, absorption in the host medium,

and diffraction.

Typically the imperfect mirror reﬂectivities domi-

nate the other sources of loss. If the mirror reﬂectivities

are r

and r

, then the intensity I is reduced by the fac-

tor r

in a round trip pass through the cavity, while

Part F 70

1024 Part F Quantum Optics

according to (70.1) the gain medium causes the inten-

sity to increase by a factor exp(2g) in the two passes

through the gain cell of length . Equating of the gain

and loss factors leads to the threshold condition for laser

oscillation: g ≥ g

, where the threshold gain is

=−

2

ln(r

) +α, (70.3)

α being an attenuation coefﬁcient associated with any

loss mechanisms that may exist in addition to reﬂection

losses at the mirrors.

Suppose, for example, that a laser has a 50 cm gain

cell and mirrors with reﬂectivities 0.99 and 0.97, and that

absorption within the host medium of the gain cell is neg-

ligible. Then the threshold gain is g

= 4×10

−4

−1

If the lasing transition is the 6328 Å Ne transition of the

He–Ne laser, we have A

∼

1.4×10

−1

, n

∼

1.0 and,

assuming a pure Doppler lineshape,

S(ν) =



4ln2



1/2

δν

(70.4)

at line center, where δν

is the width (FWHM)of

the Doppler lineshape (Sect. 69.3). For T = 400 K

and the Ne atomic weight, δν

∼

1500 MHz and

S(ν)

∼

6.3×10

−10

s. Then the threshold population dif-

ference required for laser oscillation is



−



8πn

AS(ν)

∼

2.8×10

−3

(70.5)

This is a typical result: the population inversion required

for laser oscillation is small compared with the total

number of active atoms.

Calculations of population inversions and other

properties of the gain medium are based on rate equa-

tions, or more generally, the density matrix ρ.Inmany

instances, the medium is fairly well described in terms

of two energy eigenstates, other states appearing only

indirectly through pumping and decay channels. In this

case, ρ is a 2 × 2 matrix whose elements satisfy [70.3]

(68.66)and(68.67)

=−(Γ

+Γ)ρ

−



Ω

∗

−Ω



=−Γ

+Γρ



Ω

∗

−Ω



=−(γ +i∆)

−

iΩ

(ρ

−ρ

), (70.6)

with

∗

. Here, Γ

and Γ

are, respectively, the

rates of decay of the upper and lower states due to

all processes other than the spontaneous decay from

state 2 to state 1 described by the rate Γ = A. γ ,which

is 2π times the homogeneous linewidth (HWHM) of

the transition, is the rate of decay of off-diagonal co-

herence due to both elastic and inelastic processes; in

general, γ ≥ (Γ

+Γ

+Γ)/2. Ω

= d

· E / is the

Rabi frequency (The Rabi frequency is often deﬁned

as 2d

· E / .) (Sect. 68.3.3 and Chapt. 73), with E the

complex amplitude of the electric ﬁeld; i. e., the electric

ﬁeld is

E(r, t) = Re



E (r, t)e

i(k·r−ωt)



∼



E (r, t) e

ikz

−iωt



(70.7)

It is assumed that E is slowly varying in time compared

with the oscillations at frequency ω(= 2πν),andthat

thewavevectork is approximately k

z = (nω/c)

z,where

z is a unit vector pointing in the direction of propagation.

Finally, ∆ = ω

−ω in (70.6) is the detuning of ω from

the central transition frequency ω

= (E

−E

)/ of

the lasing transition. Rapidly oscillating terms involving

+ω are ignored in the rotating wave approximation

that pervades nearly all of laser theory (Sect. 68.3.2).

In most lasers, γ is so large compared with the di-

agonal decay rates that the off-diagonal elements of ρ

may be assumed to relax quickly to the quasisteady

values obtained by setting

= 0in(70.6). Then the

diagonal density matrix elements satisfy the rate equa-

tions (69.37)

=−(Γ

+Γ)ρ

−

|Ω

γ/2

∆

+γ

(ρ

−ρ

=−Γ

+Γρ

|Ω

γ/2

∆

+γ

(ρ

−ρ

(70.8)

Such rate equations, usually expressed equivalently in

terms of population densities N

, N

rather than occupa-

tion probabilities ρ

,ρ

, are the basis of most practical

computer models of laser oscillation. These equations,

or, more generally, the density matrix equations, must

also include terms accounting for the pump mechanism.

In the simplest model of pumping, one adds a constant

pump rate Λ

to the right-hand side of the equation

for ρ

to obtain (69.45)

= Λ

−(Γ

+ A)ρ

−

|Ω

γ/2

∆

+γ

(ρ

−ρ

(70.9)

In the case of an inhomogeneously broadened laser tran-

sition (Sect. 69.3), equations of the type (70.6)and(70.8)

Part F 70.1

Laser Principles 70.2 Continuous Wave, Single-Mode Operation 1025

apply separately to each detuning ∆ arising from the dis-

tribution of atomic or molecular transition frequencies.

In writing these equations, we have assumed a nonde-

generate electric dipole transition. The generalization

to magnetic or multiphoton transitions, or to a case

where the ampliﬁcation is due, for instance, to a Raman

process, is straightforward but of less general interest.

A more realistic treatment of the electromagnetic

ﬁeld than that based on (70.1) proceeds from the

Maxwell equations, which, for a homogeneous and

nonmagnetic medium, lead to the equation

2ik

∇

E +



∂

∂z

∂

∂t



E =

4πiω

Nµ

∗

(70.10)

Here N is the density of active atoms, µ ≡(d

· )

∗

,and

∇

≡ ∂

/∂x

+∂

/∂y

.Theresult(70.10) assumes the

validity of the rotating wave approximation as well as

the assumption that E is slowly varying compared with

exp(ikz) and exp(−iωt). In the plane wave approxima-

tion, (70.10) becomes (More generally, the velocity c on

the left sides of (70.10)and(70.11) should be replaced by

the group velocity v

associated with nonresonant tran-

sitions. If there is substantial group velocity dispersion,

it is sometimes necessary to include a term involving the

second derivative of E with respect to t)



∂

∂z

∂

∂t



E =

4πiω

Nµ

∗

. (70.11)

Equations (70.6)or(70.8)and(70.10)or(70.11)are

coupled matter–ﬁeld equations whose self consistent

solutions determine the operating characteristics of the

laser. The density matrix or rate equations must be mod-

iﬁed to include pumping, as in (70.9), and the ﬁeld

equations must be supplemented by boundary conditions

and loss terms. With these modiﬁcations, the equations

are the basis of semiclassical laser theory, wherein the

particles constituting the gain medium are treated quan-

tum mechanically whereas the ﬁeld is treated according

to classical electromagnetic theory [70.4]. Aside from

fundamental linewidth considerations and photon statis-

tics (see Sects.70.2 and 70.4), very few aspects of lasers

require the quantum theory of radiation.

70.2 Continuous Wave, Single-Mode Operation

In the case of steady state, continuous wave (cw) oper-

ation, the appropriate matter–ﬁeld equations are those

obtained by setting all time derivatives equal to zero.

Equation (70.11), for instance, becomes

2πωN|d|

3n c

γ +i∆

(ρ

−ρ

)E , (70.12)

or, in terms of the intensity I,

4πωN|d|

3n c

∆

+γ

(ρ

−ρ

8πn

−N

)S(ν)I = g(ν)I (70.13)

for the nondegenerate case under consideration. Here,

|d|

= 3|d

· |

, N

= Nρ

, S(ν) = γ/



∆

+γ



the Lorentzian lineshape function for homogeneous

broadening, and A = 4ω

|d|

n/3 c

is the spontaneous

emission rate in the host medium of (real) refractive in-

dex n. Local (Lorentz–Lorenz) ﬁeld corrections will in

general modify these results, but such corrections are

ignored here [70.5].

The steady state solution of the density matrix or

rate equations gives, similarly,

g(ν) =

(ν)

1+I/I

sat

, (70.14)

where the saturation intensity I

sat

, like the small sig-

nal gain coefﬁcient g

(ν), depends on decay rates and

other characteristics of the lasing species. Thus, in the

plane wave approximation, the growth of intensity in

a homogeneously broadened laser medium is typically

described by the equation

(ν)I

1+I/I

sat

. (70.15)

This equation, supplemented by boundary conditions at

the mirrors, and possibly other terms on the right side

to account for any distributed losses within the medium,

determines the intensity in cw, single-mode operation.

The simplest model for calculating output intensity

assumes that the intensity is uniform throughout the laser

cavity. In steady state, the gain exactly compensates for

the loss; i. e., g(ν) = g

, the gain clamping condition for

cw lasing. Equation (70.14) then implies that the steady

state intracavity intensity is

I = I

sat

[

(ν)/g

−1

]

. (70.16)

If I is assumed to be the sum of the intensities of

waves propagating in the +z and −z directions, i. e.

I = I

−

, then the output intensity from the laser is

out

= t

−

, (70.17)

Part F 70.2