Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

1004 Part F Quantum Optics

levels of interest, is of the general form [68.16]

dρ

=−



eff

ρ −ρH

†

eff



(68.57)

where

eff

= H +

Γ, (68.58)

H being the atom-ﬁeld Hamiltonian and

Γ the non-

Hermitian relaxation operator, deﬁned by its matrix

elements

n|

Γ |m=

. (68.59)

Both inelastic collisions and spontaneous emission to

unobserved levels can be described by this form of

evolution. In the framework of this chapter, inelastic,

or strong, collisions are deﬁned as collisions that can

induce atomic transitions into other energy levels.

68.4.2 Relaxation Toward Levels of Interest

A master equation description is necessary when all

involved levels are observed [68.7, 17]. This master

equation can rapidly take a complicated form if more

than two levels are involved. We give results only for

the case of a two-level atom and upper to lower-level

spontaneous decay and elastic or soft collisions; i. e.,

collisions that change the separation of energy levels

during the collision, but leave the level populations un-

changed. In that case, the atomic master equation takes

the form

dρ

=−

[H,ρ]−

(

−

ρ +ρs

−

−2s

−

ρs

)

−

ρ +2γ

ρs

, (68.60)

where the free-space spontaneous decay rate Γ is found

from QED to be

Γ =

4π

3 c

, (68.61)

and γ

is the decay rate due to elastic collisions.

It is possible to express the classical decay rate

(68.17) in terms of the quantum spontaneous emission

rate (68.61)as

Γ = Γ

, (68.62)

where f

is the oscillator strength of the transition. The

various oscillator strengths characterizing the dipole-

allowed transitions from a ground state |e to excited

levels |e obey the Thomas–Reiche–Kuhn sum rule



= 1 , (68.63)

where the sum is on all levels dipole-coupled to |g.

Assuming that d and the polarization of the ﬁeld are

both parallel to the x-axis, this gives

2mω

|g|x|e|

. (68.64)

68.4.3 Optical Bloch Equations with Decay

In general, the optical Bloch equations cannot be gener-

alized to cases where relaxation mechanisms are present.

There are, however, two notable exceptions corres-

ponding to situations where

1. the upper level spontaneously decays to the lower

level only, while the atom undergoes only elastic

collisions;

2. spontaneous emission between the upper and lower

levels can be ignored in comparison with decay to

unobserved levels, which occur at equal rates γ

= 1/T

Under these conditions, (68.55) generalizes to

=−U/T

−∆V ,

=−V/T

+∆U +Ω

W ,

=−(W −W

)/T

−Ω

V , (68.65)

where we have introduced the longitudinal and trans-

verse relaxation times T

and T

, with T

= 1/Γ and

=(1/2T

+γ

)

−1

in the ﬁrst case, and T

=(1/T

)

−1

in the second case. The equilibrium inver-

sion W

is equal to zero in the second case since the

decay is to unobserved levels.

68.4.4 Density Matrix Equations

In the general case, it is necessary to consider the density

operator equation (68.43) instead of the optical Bloch

equations. The equations of motion for the components

of ρ become, for the general case of complex Ω

dρ

=−γ

−



iΩ

∗

+c.c.



dρ

=−γ



iΩ

∗

+c.c.



=−(γ +i∆)

−i

Ω



−ρ



(68.66)

Part F 68.4

Light–Matter Interaction 68.5 Rate Equation Approximation 1005

where γ = (γ

+γ

)/2 +γ

,and

= ρ

iωt

.Inthe

case of spontaneous decay from the upper to the lower

level, these equations become

dρ

=−Γρ

−



iΩ

∗

+c.c.



dρ

=+Γρ



iΩ

∗

+c.c.



=−(γ +i∆)

−i

Ω



−ρ



(68.67)

where γ = Γ/2 +γ

. Equations (68.67) are completely

equivalent to the optical Bloch equations (68.65).

68.5 Rate Equation Approximation

If the coherence decay rate γ is dominated by elastic

collisions, and hence is much larger than the population

decay rates γ

and γ

can be adiabatically eliminated

from the equations of motion (68.66)and(68.67)to

obtain the rate equations (Sect. 68.2)

dρ

=−γ

− R



−ρ



dρ

=−γ

+ R



−ρ



(68.68)

and

dρ

=−Γρ

− R



−ρ



dρ

=+Γρ

+ R



−ρ



(68.69)

respectively, where the transition rate is

R =|Ω

L(∆)/(2γ) , (68.70)

and we have introduced the dimensionless Lorentzian

L(∆) =γ



+∆



(68.71)

The transitions between the upper and lower state are

thus described in terms of simple rate equations.

Adding phenomenological pumping rates Λ

and Λ

on the right-hand side of (68.68) provides a description

of the excitation of the upper and lower levels from

some distant levels, as would be the case in a laser. The

equations then form the basis of conventional, single-

mode laser theory. In the absence of such mechanisms,

the atomic populations eventually decay away.

68.5.1 Steady State

In the case of upper to lower-level decay, the state

populations reach a steady state with inversion [68.5,17]

=−

Γ +2R

=−

1 +s

(68.72)

where s is the saturation parameter. In the case of pure

radiative decay, γ

= 0, s is given by

s =

Ω

/4 +∆

. (68.73)

In steady state, the other two components of the Bloch

vector U are given by

=−

2∆

Ω



1 +s



(68.74)

and

Ω



1 +s



(68.75)

varies as a dispersion curve as a function of the de-

tuning ∆, while V

is a Lorentzian of power-broadened

half-width at half maximum



/4 +Ω



1/2

68.5.2 Saturation

As the intensity of the driving ﬁeld, or Ω

, increases,

and V

ﬁrst increase linearly with Ω

, reach a max-

imum, and ﬁnally tend to zero as Ω

→∞.The

inversion W

, which equals −1forΩ

= 0, ﬁrst in-

creases quadratically, and asymptotically approaches

= 0asΩ

→∞. At this point, where the upper and

lower state populations are equal, the transition is said to

be saturated, and the medium becomes effectively trans-

parent, or bleached. (This should not be confused with

self-induced transparency discussed in Chapt. 73.) The

inversion is always negative, which means in particular

that no steady-sate light ampliﬁcation can be achieved

in this system. This is one reason why external pump

mechanisms are required in lasers.

68.5.3 Einstein A and B Coefﬁcients

When atoms interact with broadband radiation instead

of the monochromatic ﬁelds considered so far, (68.69)

Part F 68.5

1006 Part F Quantum Optics

still apply, but the rate R becomes

R → B

(ω) , (68.76)

where (ω) is the spectral energy density of the in-

ducing radiation. Einstein’s A and B coefﬁcients apply

to an atom in thermal equilibrium with the ﬁeld,

which is described by Planck’s black-body radiation

law

(ω) =

ω/k

−1

(68.77)

where T is the temperature of the source and k

Boltzmann’s constant. Invoking the principle of detailed

balance, which states that at thermal equilibrium, the av-

erage number of transitions between arbitrary states |i

and |k must be equal to the number of transitions

between |k and |i, one ﬁnds

, (68.78)

where A

is the rate of spontaneous emission from |k

to |i,andΓ



is the level width.

68.6 Light Scattering

Far from resonance, the approximation of a two- or few-

level atom is no longer adequate. Two limiting cases,

which are always far from resonance, are Rayleigh scat-

tering for low frequencies, and Thomson scattering for

high frequencies.

68.6.1 Rayleigh Scattering

Rayleigh scattering is the elastic scattering of a mono-

chromatic electromagnetic ﬁeld of frequency ω,wave

vector k and polarization  by an atomic system in the

limit where ω is very small compared with its excita-

tion energies [68.4,17]. To second-order in perturbation

theory, the Rayleigh scattering differential cross section

into the solid angle Ω



about the wave vector k



with



= k, and polarization 



dσ

dΩ



( · 



)







, (68.79)

where r

is the classical electron radius, the sum is over

all states |e, f

is the E1 oscillator strength (68.64)and

is the transition frequency. The corresponding total

cross section is

σ =

8πr







. (68.80)

68.6.2 Thomson Scattering

Thomson scattering is the corresponding elastic photon

scattering by an atom in the limit where ω is very large

compared with the atomic ionization energy, yet small

enough compared to αmc

/ , that the dipole approxi-

mation can be applied. The differential cross section for

this process is [68.4,17]

dσ

dΩ





 · 



, (68.81)

and the total cross section is

σ =

πr

. (68.82)

This is a completely classical result, which exhibits no

frequency dependence.

68.6.3 Resonant Scattering

We ﬁnally consider elastic scattering in the limit where

ω is close to the transition frequency ω

between |g

and |e. Provided that no other level is near-resonant

with the ground state, the resonant scattering differential

cross section is [68.6,17]

dσ

dΩ



16π



 · 



(Γ/2)

∆

+(Γ/2)

, (68.83)

where λ

= 2πc/ω

is the wavelength of the transition

and Γ is the spontaneous decay rate (68.61). The total

elastic scattering cross section is

σ =

2π

. (68.84)

In contrast to the nonresonant Rayleigh and Thom-

son scattering cross sections, which scale as the square

of the classical electron radius, the resonant scattering

cross section scales as the square of the wavelength. For

optical to frequencies, λ

 10

,givingaresonant

enhancement of about eight orders of magnitude. This

illustrates why near resonant phenomena, which form

the bulk of the following chapters, are so important in

optical physics and quantum optics.

Part F 68.6

Light–Matter Interaction References 1007

References

68.1 B. W. Shore: The Theory of Coherent Atomic Excita-

tion (Wiley-Interscience, New York 1990)

68.2 C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg:

Photons and Atoms: Introduction to Quantum

Electrodynamics (Wiley-Interscience, New York

1989)

68.3 A. Sommerfeld: Optics (Academic, New York 1967)

68.4 J. D. Jackson: Classical Electrodynamics (Wiley, New

York 1975)

68.5 L. Allen, J. H. Eberly: Optical Resonance and Two-

Level Atoms (Dover, New York 1987)

68.6 P. W. Milonni, J. H. Eberly: Lasers (Wiley-Inter-

science, New York 1988)

68.7 P. Meystre, M. Sargent III: Elements of Quantum

Optics, 3rd edn. (Springer, Berlin, Heidelberg 1999)

68.8 M.Born,E.Wolf:Principles of Optics, 4th edn.

(Pergamon, Oxford 1970)

68.9 R. J. Glauber: Optical coherence and photon statis-

tics. In: Quantum Optics and Electronics,ed.by

C. DeWitt, A. Blandin, C. Cohen-Tannoudji (Gordon

and Breach, New York 1965)

68.10 L. Mandel, E. Wolf: Optical Coherence and Quan-

tum Optics (Cambridge Univ. Press, Cambridge

1995)

68.11 M. S. Zubairy, M. O. Scully: Quantum Optics (Cam-

bridge Univ. Press, Cambridge 1997)

68.12 Y. R. Shen: The Principles of Nonlinear Optics (Wiley,

New York 1984)

68.13 M. Orszag: Quantum Optics (Springer, Berlin, Hei-

delberg 2000)

68.14 W. P. Schleich: Quantum Optics in Phase Space

(Wiley-VCH, Weinheim 2001)

68.15 M. Sargent III, M. O. Scully Jr., W. E. Lamb: Laser

Physics (Wiley, Reading 1977)

68.16 S. Stenholm: Foundations of Laser Spectroscopy

(Wiley-Interscience, New York 1984)

68.17 C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg:

Atom-Photon Interactions: Basic Processes and

Applications (Wiley-Interscience, New York 1992)

68.18 P. L. Knight, P. W. Milonni: Phys. Rep. 66, 21 (1980)

68.19 P. P. Berman (Ed.): Cavity QED (Academic, Boston

1994)

68.20 C. Cohen-Tannoudji: Atomic motion in laser light.

In: Fundamental Systems in Quantum Optics,ed.by

J. Dalibard, J. M. Raimond, J. Zinn-Justin (North-

Holland, Amsterdam 1992)

68.21 R. P. Feynman, F. L. Vernon, R. W. Hellwarth:

J. Appl. Phys. 28, 49 (1957)

Part F 68

1009

Absorption an

69. Absorption and Gain Spectra

This chapter develops theoretical techniques to

describe absorption and emission spectra, using

concepts introduced in Chapt. 68, and density ma-

trix methods from Chapt. 7. The simplest cases are

treated, compatible with the physics involved, and

more realistic applications are referred to in other

chapters. Vector notation is not used, but it can

be inserted as required. Only steady-state spec-

troscopy is covered; for time-resolved transient

techniques see Chapt. 73.

Laser technology has greatly expanded the

potential of atomic and molecular spectroscopy,

but the same techniques for describing the

interaction of light with matter also apply to the

traditional arc lamps and ﬂash discharges,

69.1 Index of Refraction .............................. 1009

69.2 Density Matrix Treatment

of the Two-Level Atom......................... 1010

69.3 Line Broadening..................................1011

69.4 The Rate Equation Limit .......................1013

69.5 Two-Level Doppler-Free Spectroscopy ...1015

69.6 Three-Level Spectroscopy ..................... 1016

69.7 Special Effects in Three-Level Systems ...1018

69.8 Summary of the Literature ...................1020

References .................................................. 1020

and the more recent synchrotron radiation

sources.

In many cases, departures from the thin sample limit,

such as beam attenuation, light scattering and radiation

trapping (Sect. 69.2) may be important. However, the

properties of laser devices themselves depend in an es-

sential way on these effects, making a self-consistent

treatment of their properties necessary.

At the other extreme, the spectroscopy of dilute gases

is well characterized by ensemble averages over the

properties of the individual particles, interrupted by oc-

casional brief collisions. Ensemble averages, however,

may no longer apply to recent experiments probing a sin-

gle atomic particle in a trap, as discussed in Chapt. 75.

69.1 IndexofRefraction

As discussed in Sect. 68.2.2, the complex index of re-

fraction for a medium containing harmonically bound

charges (electrons) [69.1] with natural frequency ω

n(ω) =



1 +

Nα(ω)

≈ 1 +

Nα(ω)

2ε

= 1 +

2mε



iγω +



−ω





−ω



+γ



= n



+i n



. (69.1)

The expansion is valid when the density of atoms N is

low.

A plane wave can be written in the form

E ∝ e

ikz

= e

iωnz/c

= e

iωn



z/c

−ωn



z/c

. (69.2)

The absorption of light through the medium then shows

a resonant behavior near ω ≈ω

determined by



2mε



γω



−ω



+γ



≈

πNe

4mε



γ/2π

(ω −ω

)

+γ



(69.3)

This is called an absorptive lineshape. When the sin-

gle electron is harmonically bound, its interaction with

radiation is found in this response. For a real atom,

the response of the electron is divided among the vari-

ous transitions to other states. The fraction assigned to

one single transition is characterized by the oscillator

strength f

as discussed in Sect. 68.4.2.

In ordinary linear spectroscopy, the laser is tuned

through the resonance ω ≈ ω

, and the value of ω

Part F 69

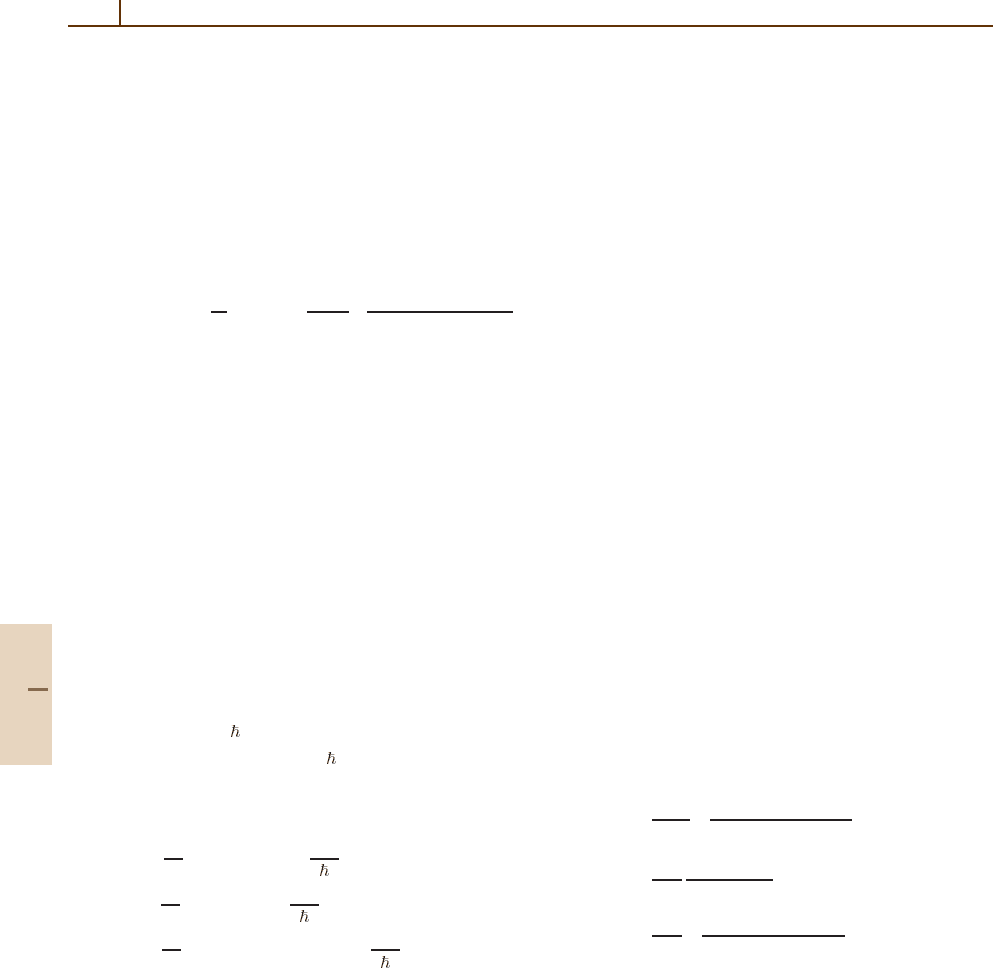
1010 Part F Quantum Optics

determined from the lineshape (69.3). Several closely

spaced resonances can be resolved if their spacing is

larger than their widths



(1)

−ω

(2)



>γ .

(69.4)

This deﬁnes the spectral resolution (Chapt. 10).

The velocity of light in the medium is seen to be

given by the expression

eff



≈ c



1 −

2mε



−ω



−ω



+γ



(69.5)

This expression shows a dispersive behavior around

the position ω = ω

, where the modiﬁcation of the

velocity disappears. Below resonance ω<ω

,theve-

locity of light is lower than in vacuum. This derives

from the fact that the polarization is in phase with

the driving ﬁeld. Thus, by storing the incoming en-

ergy, the driving ﬁeld retards the propagation of the

radiation.

For a harmonically bound charge, the refractive in-

dex (69.1) always stays absorptive and it is independent

of the intensity of the laser radiation. This no longer

holds for discrete level atomic systems. In order to

see this, we consider the two-level atom in Sect. 69.2

(Sect. 68.3).

69.2 Density Matrix Treatment of the Two-Level Atom

The response of atoms to light is conveniently ex-

pressed in terms of the density matrix ρ. In addition

to the direct physical meaning of the density matrix

elements discussed in Sect. 68.3.3, the density matrix

formalism is advantageous because the various relax-

ation mechanisms effecting the atomic resonances can

be introduced phenomenologically into its equations

of motion (Sect. 68.4), and theoretical derivations of-

ten provide master equations for the density matrix

(Chapt. 7).

The two-level Hamiltonian (68.35) can be written as

H =



/2 −dE (R , t)

−dE (R, t) −



(69.6)

The equation of motion for the density matrix (68.67)is

then

=−Γρ

idE

cos ωt



−ρ



= Γρ

−

idE

cos ωt



−ρ



=−(γ +iω

)ρ

idE

cos ωt



−ρ



(69.7)

Here Γ is the spontaneous decay rate given by (68.61)

and

γ = Γ/2 +γ

, (69.8)

where γ

derives from all processes that tend to ran-

domize the phase between the quantum states |e and

|g, such as collisions (Chapts. 7 and 19), noise in the

laser ﬁelds and thermal excitation of the environment

in solid state spectroscopy. The Greek letters Γ and

γ correspond to the longitudinal relaxation rate (T

process) and the transverse relaxation rate (T

-process),

respectively (Sect. 68.4.3).

In the rotating wave approximation (RW A), dis-

cussed in Sect. 68.3.2, the density matrix equations

(69.7) become identical to (68.67) with

−iωt

. (69.9)

Using t he condition of conservation of probability

+ρ

= 1 , (69.10)

the steady state solutions to (68.67) are [69.2]

Ω

2Γ



∆

+γ

+Ω

γ/Γ



(69.11)

iΩ



−ρ



γ +i∆

iΩ



γ −i∆

∆

+γ

+Ω

γ/Γ



(69.12)

where Ω

is the Rabi frequency from (68.44), and ∆ =

−ω is the detuning. The induced polarization is then

P = N Tr



dρ



= N Tr



0 d

d 0





= Nd



−iωt

+ e

iωt



= N



αE

(+)

+α

∗

(−)



(69.13)

Part F 69.2

Absorption and Gain Spectra 69.3 Line Broadening 1011

where N is the density of active two-level atoms. Setting

(+)

E e

−iωt

, (69.14)

the complex polarization is

α(ω) =



iγ +∆

∆

+γ

+Ω

γ/Γ



(69.15)

and from (69.1), the complex index of refraction is

n(ω) = 1 +

Nα(ω)

2ε

= 1 +

πNe

4ε

mω





iγ +∆

∆

+γ

+Ω

γ/Γ

(69.16)

where f

=2d

mω

/ e

is the oscillator strength. Sum-

ming over all possible transitions yields the f-sum

rule (68.63)(Chapt.21).

The imaginary part of (69.16) shows exactly the

same absorptive behavior as in the harmonic oscillator

model of Sect. 69.1 [see (69.3)]. However, the additional

factor of



Ω

γ/Γ



in the denominator makes the line

appear broader than in the harmonic case; the line is

power broadened. Physically, this derives from a satu-

ration of the two-level system in which the population

of the upper level becomes an appreciable fraction of

that of the lower level. In the limit Ω

→∞,(69.16)

shows that n(ω) →1 and the atom-ﬁeld interaction ef-

fectively vanishes. In this limit, ρ

→

(69.11), and the

ﬁeld induces as many upward transitions as downward

transitions.

When radiation at the frequency ω propagates in

a medium of two-level atoms, the energy density is

I(z) ∝ E

∗

E ∝ exp



−





γz

(ω −ω

)

+γ



(69.17)

Far from resonance (|ω −ω

|γ ), the medium is

transparent; but near resonance, damping is observed.

The impinging radiation energy is deposited in the

medium and propagation is impeded. This is called ra-

diation trapping. In spectroscopy, the phenomenon is

seen as a prolongation of the radiative decay time; the

spontaneously emitted energy is seen to emerge from

the sample more slowly than the single atom lifetime

implies.

69.3 Line Broadening

The effective width of a spectral line from (69.16)is

eff



+Ω



Γ +γ

Ω

2Γ



Ω



(69.18)

The various contributions are as follows [69.3]. The

term γ contains all the transverse relaxation mechan-

isms. If decay to additional levels occurs, these must be

included (Sect. 69.4). The term γ

contains all perturb-

ing effects effecting each single atom. For low enough

pressures, collisional perturbations are proportional to

the density of perturbing atoms so that

= η

coll

p , (69.19)

where p is the pressure of the perturbing gas and η

coll

is a constant of proportionality. This is called colli-

sion or pressure broadening (Chapt. 59), whose order

of magnitude can be estimated to be the inverse of the

average free time between collisions. For high pressure

(usually of the order of torrs), the linearity in (69.19)

breaks down. When identical atoms collide, resonant

exchange of energy may also take place. The third term

in (69.18)isthepower broadening term. It derives from

the effect of the laser ﬁeld on each individual atom. All

such relaxation processes that are active on each and ev-

ery individual atom separately are called homogeneous

broadening processes. For a detailed discussion of line

broadening, consult Chapt. 19.

In contrast to homogeneous broadening, Doppler

broadening is characterized by an atomic velocity par-

ameter v which varies over the observed assembly. In

a thermal assembly at temperature T (e.g., a gas cell),

the velocity distribution is

P(v) =

√

2πu

exp



−



(69.20)

where u

= k

T/M. A particular atom with velocity v

in the direction of the optical beam with wave vector k

then experiences the Doppler-shifted frequency ω −kv

relative to a stationary atom, and the effective detuning

becomes

∆



= ∆ +kv, (69.21)

Part F 69.3

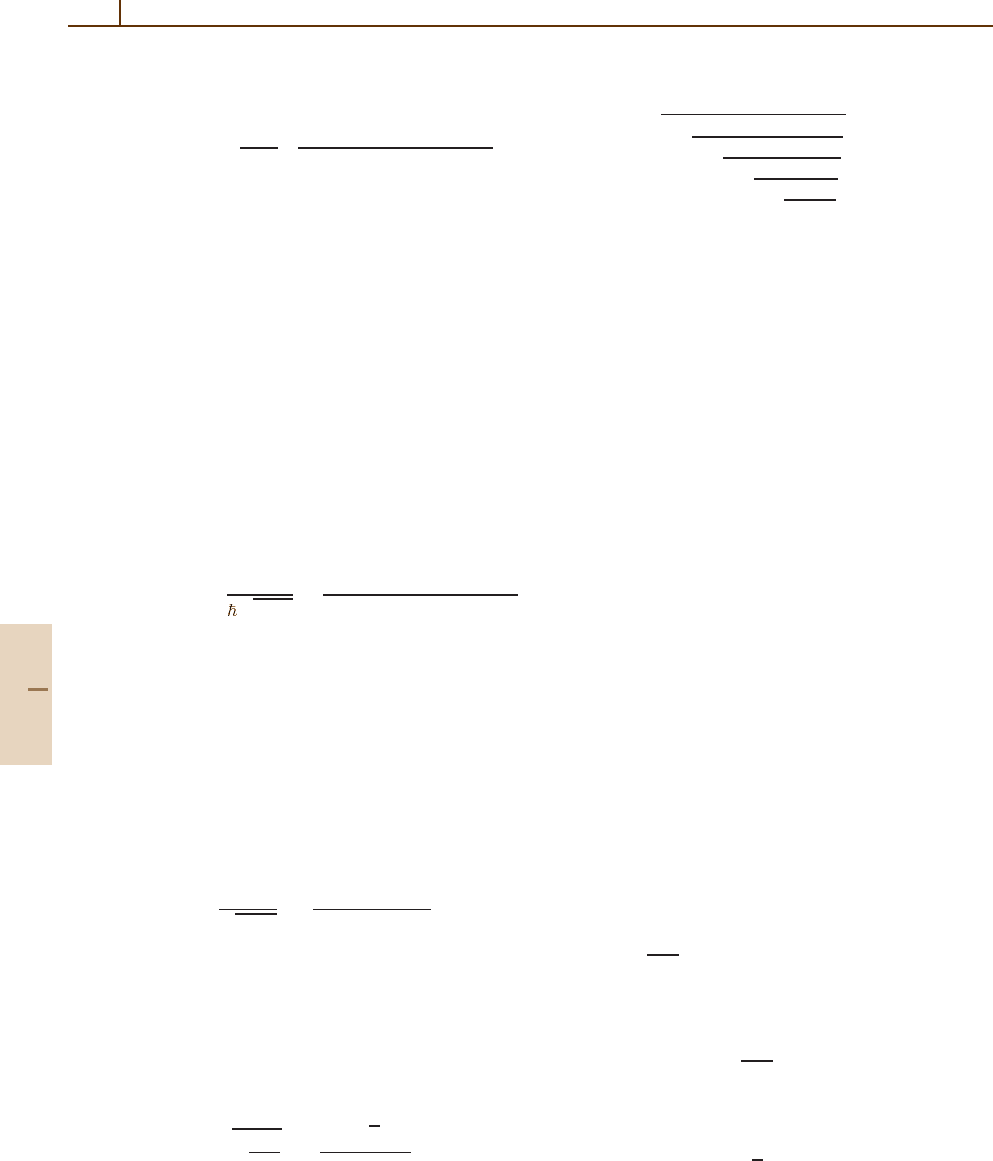
1012 Part F Quantum Optics

replacing ∆. The population in the lower level from

(69.11)isthen

= 1 −

Ω

2Γ



(∆ +kv)

+γ

+Ω

γ/Γ



(69.22)

The atoms in the lower level, originally distributed ac-

cordingto(69.20), are now depleted from the velocity

group around

v = (ω −ω

)/k . (69.23)

The width of the depleted region is given by γ

eff

of (69.18). This region is called a Bennett hole.When

the laser frequency ω is tuned, the hole sweeps over the

velocity distribution of the atoms. The atomic response

is saturated at the velocity group of the hole, indicating

that spectral hole burning has occurred.

The observed spectrum is obtained by averaging the

single atom response (69.15) over the velocity distribu-

tion. From the imaginary part, the absorption response



(ω) =

√

2πu

+∞



−∞

γ e

−v

/2u

(∆ +kv)

+γ

+Ω

γ/Γ

dv.

(69.24)

In the limits Ω

→ 0 (no saturation), and γ  ku (the

Doppler limit), the Lorentzian line shape sweeps over

the entire velocity proﬁle, ﬁnding a resonant velocity

group according to (69.23) as long as v ≤ u. Thus, the

linear spectroscopy sees a Doppler broadened line of

width ku.Thisiscalledinhomogeneous broadening.

In the unsaturated regime, the atomic response func-

tion (69.24) is proportional to the imaginary part of the

function

V(z) =

√

2πσ

+∞



−∞

exp



−x

/2σ



z −x

dx ,

(69.25)

at z =−∆ −iγ and σ = ku. This is the Hilbert trans-

form of the Gaussian, and its shape is called a Vo i gt

proﬁle [69.4]. For γ  ku , it traces over the Gaussian,

but for large detunings it always goes to zero as slowly

as the Lorentzian, i. e., as ∆

−1

. The proﬁle has been

widely used to interpret the data of linear spectroscopy.

The function is tabulated [69.5] and its expansion is

V(z) =



−

2σ

∞



n=0



iz/

√

2σ



(

1 +n/2

)

(69.26)

and it has the continued fraction representation,

V(z) =

z −

2σ

z −

3σ

z −

4σ

z −···

(69.27)

In addition to velocity, any other parameter shifting the

individual atomic resonance frequencies ω

by different

amounts for the different individuals leads to inhomoge-

neous broadening. The detuning ∆ is then different for

different members of the observed assembly, and a line

shape similar to (69.24) applies. The distribution func-

tion must be replaced by the one relevant for the problem.

In practice a Gaussian is almost always assumed.

An example of inhomogeneous broadening is the

inﬂuence of the lattice environment on impurity spec-

troscopy in solids. The resonant light selectively excites

atoms at those particular positions which make the atoms

resonant. Thus only these spatial locations are saturated,

and the phenomenon of spatial hole burning occurs.

This has been investigated as a method for storing

information, signal processing, and volume holography.

It is, however, possible that the effects of collisions

can counteract the inhomogeneous broadening. In order

to see this we observe that the induced atomic dipole

is proportional to the induced density matrix element,

from (69.9),

i(kz(t)−ωt)

∝ e

ikvt

. (69.28)

If the atoms now experience collisions characterized by

an average free time of ﬂight τ, the phase kvt cannot

build up coherently for times longer than this duration,

the atomic velocity is quenched on the average, and the

full Doppler proﬁle cannot be observed. To see how

this comes about, consider a time t  τ. During this

period the atom experiences on the average

n =t/τ col-

lisions. Assuming a Poisson distribution, the probability

of n collisions in time t is

−

. (69.29)

Taking the average of (69.28) over the time t = nτ with

the distribution p

yields

∝

∞



n=0

ikvτn



−



= e

−

exp



n e

ikvτ



≈ e

ikvt

exp



−



. (69.30)

Part F 69.3

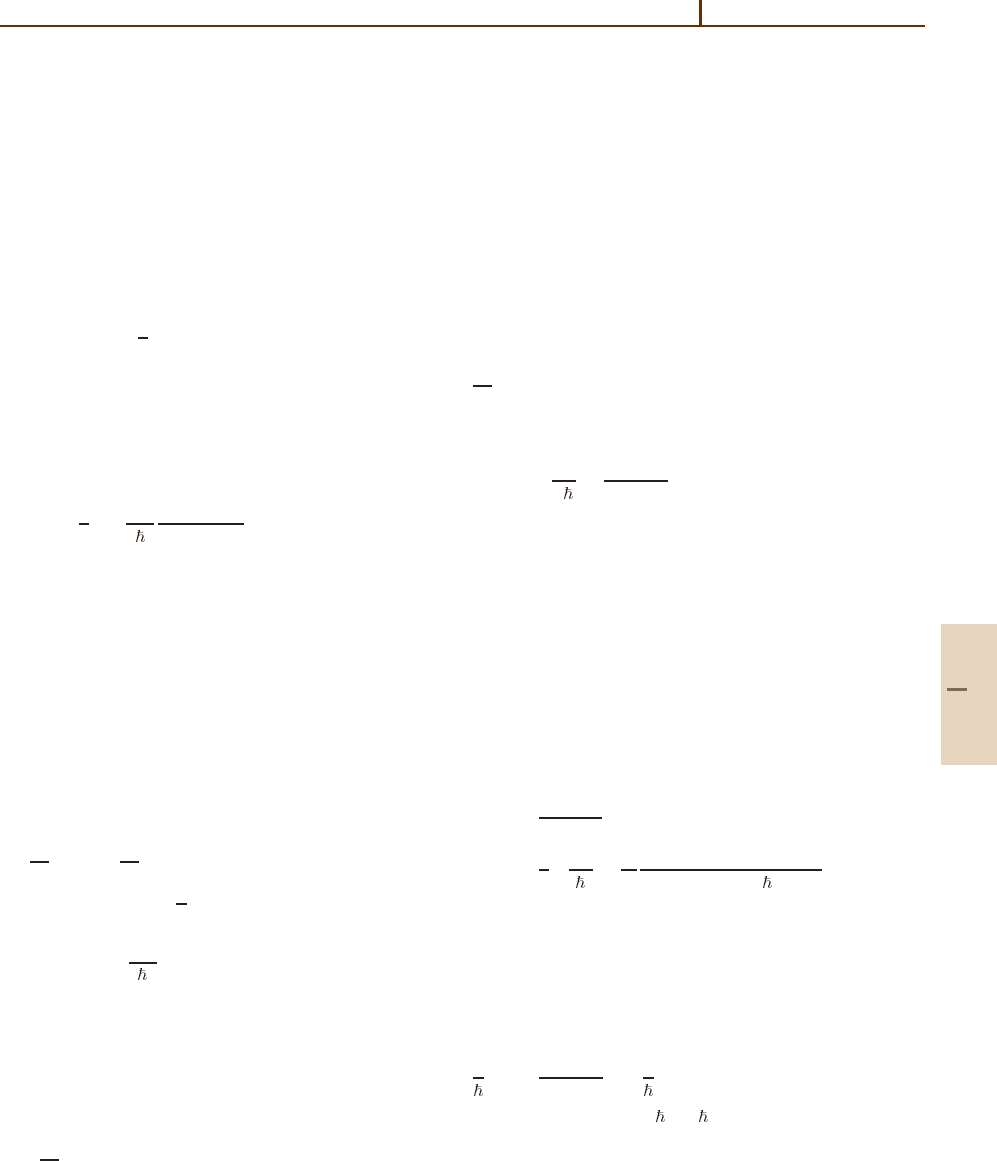
Absorption and Gain Spectra 69.4 The Rate Equation Limit 1013

This heuristic derivation suggests that for long enough

interaction times (t  τ), the large velocity com-

ponents are suppressed. This tends to prevent the

tails of the velocity distribution from contribut-

ing to the observed spectral proﬁle. The effect is

called collisional narrowing or Dicke narrowing.It

is an observable effect, but the narrowing cannot

be very large. To overcome the Doppler broaden-

ing one has to turn to nonlinear laser methods

(Sect. 69.5).

69.4 The Rate Equation Limit

Consider now a generalized theory for the case of several

incoming electromagnetic ﬁelds of the form

E (R, t) =



(R) e

−iω

t+iϕ

+c.c.. (69.31)

The index i may range over several laser sources, the

output of a multimode laser or the multitude of compon-

ents of a ﬂashlight or a thermal source. Each component

carries its own amplitude E

In steady state, the generalization of (69.12) becomes





−ρ



γ +i∆

−iω

t+iϕ

, (69.32)

where the detuning is

∆

= ω

−ω

. (69.33)

The response of the atom now separates into individual

contributions oscillating at the various frequencies ω

according to



(i)

−iω

t+iϕ

. (69.34)

This resolution is of key importance to the theory.

With the multimode ﬁeld, (68.67) for the level occu-

pation probabilities become

=−

=−Γρ





−iω

t+iϕ

−c.c.



. (69.35)

Insertion of the steady state result (69.32) into this

equation yields a closed set of equations for the level oc-

cupation probabilities. These are called rate equations.

To justify the above steps, consider the single fre-

quency case again. The off-diagonal time derivatives

can be neglected when



|γ +i∆||ρ

| . (69.36)

This can be surmised to hold when the phase relaxation

contributions to γ are large (69.8) or the detuning |∆|

is large. Insertion of (69.32)into(69.35) for the single

mode case gives

=−Γρ

−W



−ρ



(69.37)

where the rate coefﬁcient is given by

W = 2π





γ/π

∆

+γ

. (69.38)

Multiplying (69.37) by the density of active atoms N

then produces the conventional rate equations for the

populations N

= Nρ

and N

= Nρ

Two physical effects can be discerned in (69.37):

induced and spontaneous emission. The term with Γ

gives the spontaneous emission which forces the entire

population to the lower level. The terms proportional

to W describe induced emission, with upward transitions

proportional to Wρ

and downward transitions propor-

tional to Wρ

. In the absence of spontaneous emission,

they strive to equalize the population of the two levels.

Using (69.10), the steady-state solution is

Γ +2W





∆

+γ

+(dE / )

γ/Γ

(69.39)

This is clearly seen to agree with the solution (69.11)as

is expected in steady state.

Although the rate equations were derived in the

limit (69.36), the rate coefﬁcient (69.38) has a special

signiﬁcance in the limit γ → 0. In this limit, the factor

lim

γ →0



γ/π

∆

+γ



δ(∆)

= δ(

ω − ω

), (69.40)

enforces energy conservation in the transition. Using

the ﬁeld in (69.14), and the interaction from (69.6), the

Part F 69.4

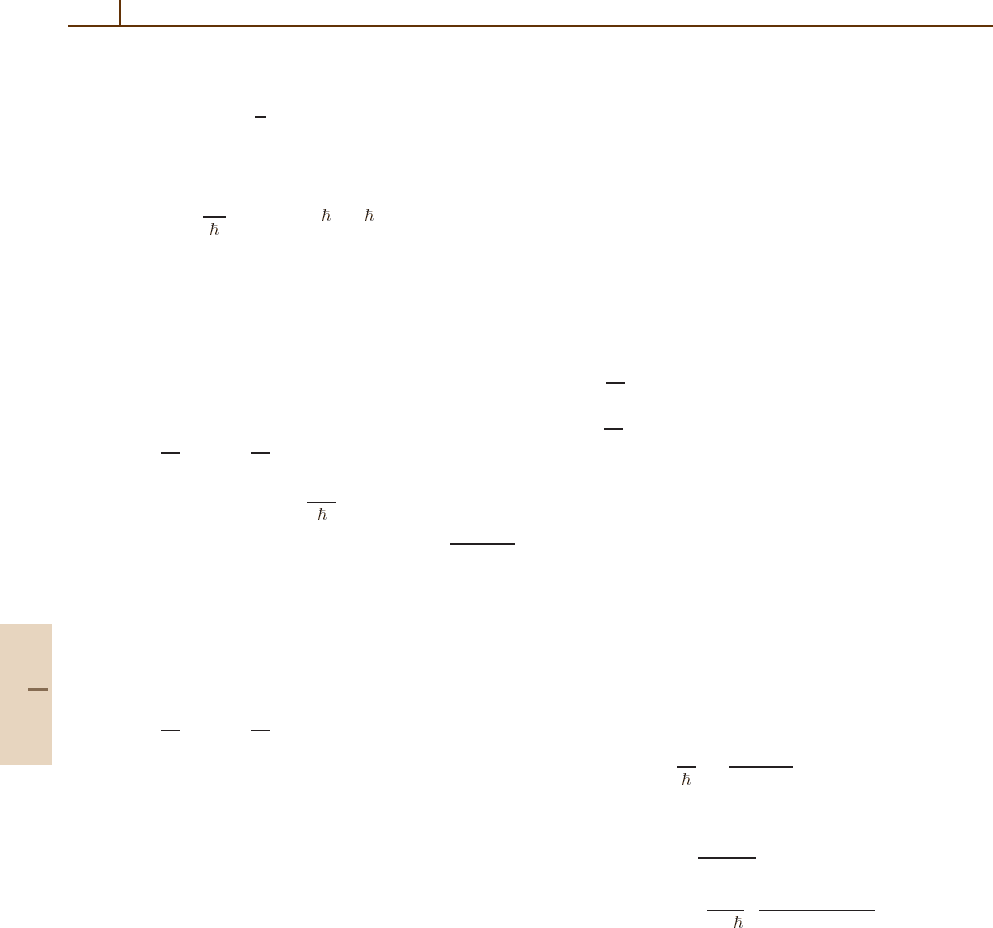
1014 Part F Quantum Optics

off-diagonal matrix element is

|e|H|g| =

dE .

(69.41)

With these results, (69.38) can be written in the form of

Fermi’s Golden Rule

W =

2π

|e|H|g|

δ( ω − ω

), (69.42)

usually derived from time dependent perturbation

theory.

Returning to the multimode rate equations, an inco-

herent broad band light source has many components

that contribute to the sum over ﬁeld frequencies. In

the case of ﬂash pulses, thermal light sources, or free-

running multimode lasers the spectral components are

uncorrelated. Inserting (69.32)into(69.35) yields

=−

=−Γρ



−ρ





i, j

i(ω

−ω

i(ϕ

−ϕ

)

∆

+γ

(69.43)

The contributions from the different terms i = j average

to zero either by beating at the frequencies |ω

−ω

| or

by incoherent effects from the random phases ϕ

. Thus,

only the coherent sum survives to give

=−

=−Γρ



(i)



−ρ



(69.44)

where the rate coefﬁcients W

(i)

are given by (69.38) with

the appropriate detunings ∆

= ω

−ω

.Thisisarate

equation in the limit of many uncorrelated components

of light, i. e., for a broad band light source. In this case

the incoherence between the different components jus-

tiﬁes the use of a rate approach, and no assumption like

(69.36) is needed. Thus, the limit γ →0(69.40) is legit-

imate, and the W

(i)

can be calculated in time dependent

perturbation theory from Fermi’s Golden Rule.

In the limit of an incoherent broad band light source,

the sum in (69.44) can be replaced by an integral. In

particular, this is allowed for incandescent light sources

as used in optical pumping experiments [69.6]. Pumping

of lasers by strong lamps or ﬂashes are also describable

by the same rate equations.

In ampliﬁers and lasers, the atoms must be brought

into states far from equilibrium by incoherent optical

excitation or resonant transfer of excitation energy in

collisions (Chapt. 70). In the two-level description, the

atomic levels are constantly replenished. The normal-

ization condition (69.10) is then no longer appropriate;

often the density matrix is normalized so that Tr(ρ)

directly gives the density of active atoms.

With pumping into the levels, one must allow for de-

cay out of the two-level system in order to prevent the

atomic density from growing in an unlimited way. This

decay takes the atom to unobserved levels. In the rate

equation approximation, the pumping and decay pro-

cesses can be described by terms added to the equations

of the form (68.68)

= λ

−γ

= λ

−γ

. (69.45)

In a laser, the level |g is usually not the ground state of

the system.

From (69.45), the steady state population is

(0)

−ρ

(0)

= λ

/γ

−λ

/γ

. (69.46)

A population inversion exists when this is negative. The

population difference (69.46) is modiﬁed when the ef-

fects of spontaneous and induced processes are added,

as in (69.37). Then the transitions saturate because of

the induced processes.

Using (69.46)in(69.12), the calculated polarizabil-

ity without saturation is

α(ω) =





iγ +∆

+∆





(0)

−ρ

(0)



(69.47)

Accordingto(69.1), the index of refraction is



(ω) = 1 +

Nα



(ω)

2ε

= 1 −



2ε



(ω −ω

)

(ω −ω

)

+γ



(0)

−ρ

(0)



(69.48)

For weakly excited atoms, ρ

≈ 1, and (69.47) agrees

with the unsaturated limit of (69.16). The dispersion of

a light signal behaving according to (69.48) is called nor-

mal, i. e., according to the harmonic model in Sect. 69.1.

Below resonance (ω<ω

), n



is larger than unity, im-

plying a reduction of the velocity of light. As a function

of ω,thecurve(69.48) starts above unity, and passes

below unity for ω>ω

.Thisisnormal dispersion.

However, for an inverted medium



(0)

<ρ

(0)



, n



less than unity for low frequencies and goes through

Part F 69.4