Dougherty С. Introduction to Econometrics, 3Ed

Подождите немного. Документ загружается.

MODELS USING TIME SERIES DATA

Exercise

12.14

Use the Salkever indirect method to compute forecasts and their standard errors for the

logarithmic demand function for your category of expenditure. Add dummy variables to the last

four observations and hence obtain the prediction errors for these years, given a regression

based on the first 32 observations. Subtract these from the actual outcomes to obtain the

forecasts. Derive a confidence interval for the forecast for 1994.

12.6 Stability Tests

Stability tests of a regression model are tests designed to evaluate whether the performance of a model

in a prediction period is compatible with its performance in the sample period used to fit it. There are

two principles on which stability tests can be constructed. One approach is to focus on the predictive

performance of the model; the other is to evaluate whether there is any evidence of shifts in the

parameters in the prediction period.

The Chow Test of Predictive Failure

In the previous section we saw that we could compute the prediction errors by adding a set of dummy

variables to the prediction period observations. It is natural to test whether the prediction errors are

significantly different from 0, and we can do this with an F test of the joint explanatory power of the

dummy variables. Combining the sample and prediction period observations, we run the regression

first without the dummy variables and then with them included. Let the residual sum of squares be

denoted RSS

and

RSS

, the subscript indicating the number of observations in the regression and

the superscript D indicating the inclusion of the dummy variables. We then see whether the

improvement in the fit on adding the dummy variables is significant, using the F test presented in

Section 4.5. The improvement is (RSS

–

RSS

); the number of dummy variables is P; the

residual sum of squares after adding the dummy variables is

RSS

; and the number of degrees of

freedom remaining is the number of observations in the combined sample, T+P, less the number of

parameters estimated, k+P. The test statistic is therefore

)/(

/)(

),(

kTRSS

PRSSRSS

kTPF

PTPT

−

=−

(12.61)

In practice, you do not even have to run the regression with the dummy variables to perform the

test, because

RSS

is identical to RSS

, the sum of the squares of the residuals in the regression

limited to the sample period. The fit for this regression is exactly the same as the fit for the first T

observations in the dummy variable regression, which means that the residuals are the same. And

there are no residuals in the last P observations of the dummy variable regression because the

MODELS USING TIME SERIES DATA

inclusion of an observation-specific dummy in each observation guarantees a perfect fit in those

observations. Hence

RSS

is exactly the same as

RSS

, and the

statistic can be written

)/(

/)(

),(

kTRSS

PRSSRSS

kTPF

TPT

−

=−

(12.62)

The test is usually known as the Chow test, after its originator, but the interpretation given here is later

(Pesaran, Smith, and Yeo, 1985).

Example

The housing services expenditure function was fitted first for the period 1959–90, giving

RSS

0.008958, and then for the period 1959–1994, giving

RSS

= 0.009218. The

statistic is therefore

21.0

29/009218.0

4/)008958.0009218.0(

)29,4(

−

(12.63)

The null hypothesis is that the coefficients of the dummy variables are all equal to 0. Since the

statistic is less than 1, we do not reject it at any significance level. There is no significant difference

between the sample period and prediction period fits and so we conclude that the model is stable.

F Test of Coefficient Stability

If there are sufficient observations in the prediction period, you can perform a Chow test on the lines

of that discussed in Chapter 6 to evaluate whether the coefficients in the sample period and prediction

period appear to be significantly different. To perform the test, you run the regression for the sample

and prediction periods separately, and then for the two periods combined, and see whether sample

period/prediction period division results in a significant improvement in fit compared with that

obtained with the combined regression. If it does, this is evidence that the coefficients are unstable.

Example

In the case of the housing services expenditure function, with the observations for 1959–1990 being

used as the sample period and those for 1991–1994 as the prediction period, the sums of the squares of

the residuals for the sample period, prediction period, and combination were 0.008958, 0.000002, and

0.009218, respectively. Running separate regressions for the two subperiods costs three degrees of

freedom, and the number of degrees of freedom remaining after estimating six parameters (constant

twice, coefficient of

LGDPI

twice, and coefficient of

LGPRHOUS

twice) is 30. Hence we obtain the

following

statistic, which is distributed with 3 and 30 degrees of freedom:

29.0

30/)000002.0008958.0(

3/])000002.0008958.0[009218.0(

)30,3(

+−

(12.64)

MODELS USING TIME SERIES DATA

Thus we conclude that there is no evidence of coefficient instability.

Exercises

12.15

Fit the logarithmic form of your demand function for your category of expenditure for the

periods 1959–1990 and 1959–1994 and perform the Chow test of predictive failure.

12.16

Fit your demand function to the data for 1959–1994, 1959–1990 and 1991–94 and perform the

F test of coefficient stability.



AUTOCORRELATION

13.1 Definition of Autocorrelation

To this point it has been assumed that the third Gauss–Markov condition, that the value taken by the

disturbance term in any observation be determined independently of its values in all the other

observations, is satisfied, and hence that the population covariance of

and

is 0, for

≠

. . When

the condition is not satisfied, the disturbance term is said to be subject to autocorrelation, often called

serial correlation (the terms are interchangeable).

The consequences of autocorrelation for OLS are somewhat similar to those of heteroscedasticity.

In general, the regression coefficients remain unbiased, but OLS is inefficient because one can find an

alternative unbiased estimator with smaller variance. The other main consequence, which should not

be mixed up with the first, is that the standard errors are estimated wrongly, probably being biased

downwards. Finally, although in general autocorrelation does not cause OLS estimates to be biased,

there is an important special case where it does.

Possible Causes of Autocorrelation

Autocorrelation normally occurs only in regression analysis using time series data. The disturbance

term in a regression equation picks up the influence of those variables affecting the dependent variable

that have not been included in the regression equation. If the value of

in any observation is to be

independent of its value in the previous one, the value of any variable hidden in

must be

uncorrelated with its value at the time of the previous observation.

Persistence of the effects of excluded variables is probably the most frequent cause of positive

autocorrelation, the usual type in economic analysis. In Figure 13.1,

depends on

and a number of

minor variables not included explicitly in the specification. The disturbance term in the model is

generated by the combined effects of these excluded variables. In the first observation, the excluded

variables have a net positive effect and the disturbance term is positive. If the excluded variables

change slowly, their positive effect will persist and the disturbance term will remain positive.

Eventually the balance will change and the net effect of the excluded variables becomes negative.

Now the persistence effect works the other way and the disturbance term remains negative for a few

observations. The duration and amplitude of each positive and negative sequence are essentially

random, but overall there will be a tendency for positive values of the disturbance term to be followed

by positive ones and for negative values to be followed by negative ones.

One important point to note is that autocorrelation is on the whole more likely to be a problem,

the shorter the interval between observations. Obviously, the longer the interval, the less likely are the

effects of the excluded variables to persist from one observation to the next.

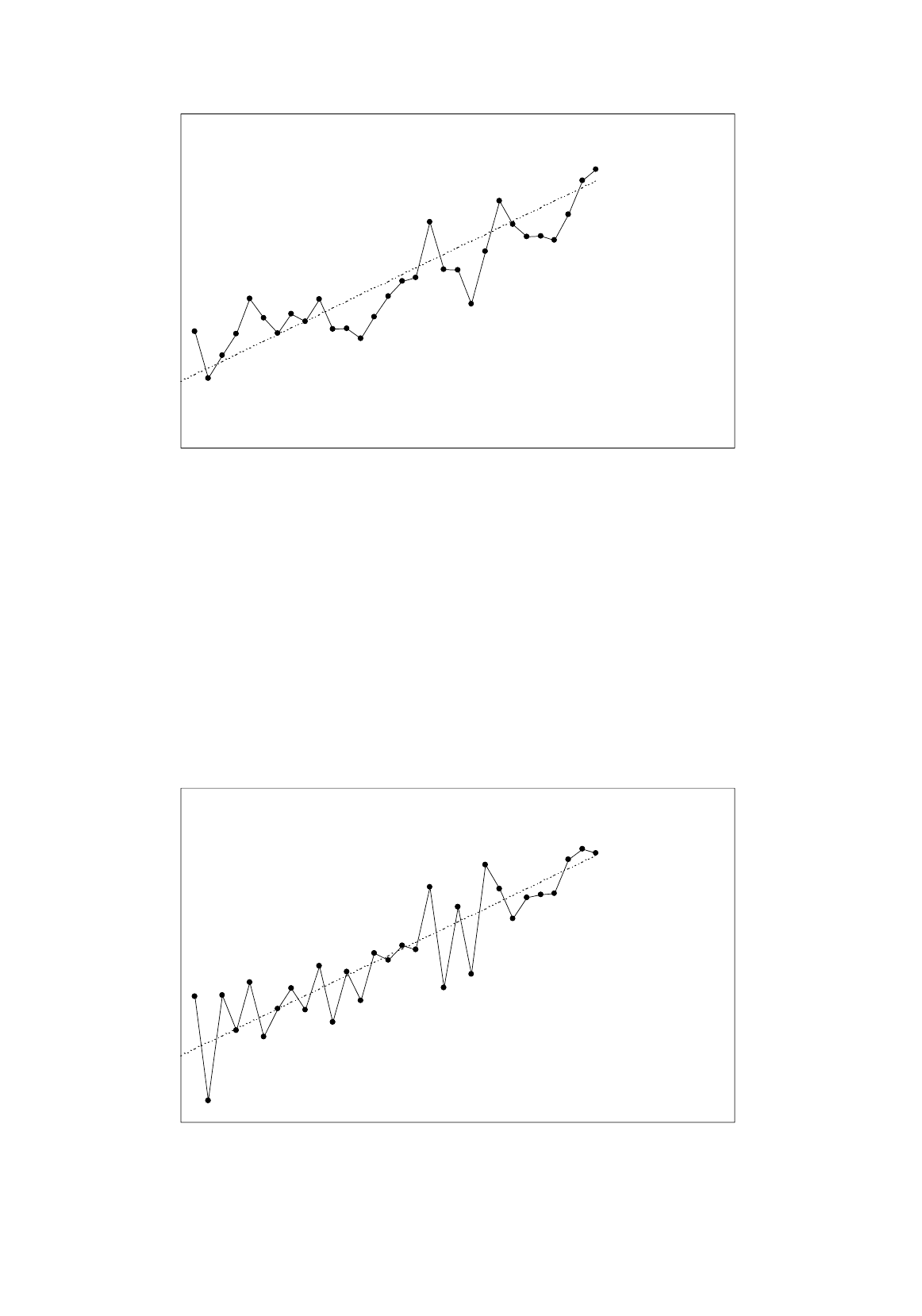
AUTOCORRELATION

Figure 13.1.

Positive autocorrelation

In principle autocorrelation may also be negative. This means that the correlation between

successive values of the disturbance term is negative. A positive value in one observation is more

likely to be followed by a negative value than a positive value in the next, and vice versa, the scatter

diagram looking like Figure 13.2. A line joining successive observations to one another would cross

the line relating Y to X with greater frequency than one would expect if the values of the disturbance

term were independent of each other. Economic examples of negative autocorrelation are relatively

uncommon, but sometimes it is induced by manipulations used to transform the original specification

of a model into a form suitable for regression analysis.

Figure 13.2.

Negative autocorrelation

AUTOCORRELATION

13.2 Detection of First-Order Autocorrelation: the Durbin–Watson Test

We will mostly be concerned with first-order autoregressive autocorrelation, often denoted AR(1),

where the disturbance term u in the model

+ u

(13.1)

is generated by the process

–1

, (13.2)

where

is a random variable whose value in any observation is independent of its value in all the

other observations. This type of autocorrelation is described as autoregressive because u

is being

determined by lagged values of itself plus the fresh element of randomness

, sometimes described as

an innovation. It is described as first-order because u

depends only on u

–1

and the innovation. A

process of the type

–1

–2

–3

–4

–5

, (13.3)

would be described as fifth-order autoregressive autocorrelation, denoted AR(5). The main alternative

to autoregressive autocorrelation is moving average (MA) autocorrelation, where u

is determined as a

weighted sum of current and previous values of

. For example, the process

–1

–2

–3

(13.4)

would be described as MA(3).

We will focus on AR(1) autocorrelation because it appears to be the most common type, at least

as an approximation. It is described as positive or negative according to the sign of

in (13.2). Note

that if

is 0, there is no autocorrelation after all.

Because AR(1) is such a common form of autocorrelation, the standard test statistic for it, the

Durbin–Watson d statistic, is usually included in the basic diagnostic statistics printed out with the

regression results. It is calculated from the residuals using the expression

)(

−

∑

−∑

(13.5)

It can be shown (see Appendix 13.1) that in large samples

→

2 – 2

(13.6)

AUTOCORRELATION

If there is no autocorrelation present,

is 0, so d should be close to 2. If there is positive

autocorrelation, d will tend to be less than 2. If there is negative autocorrelation, it will tend to be

greater than 2. The test assumes that

lies in the interval –1 >

> 1 and hence that d lies between 4

and 0.

The null hypothesis for the test is that

is equal to 0. Of course, even if H

is true, d will not be

exactly equal to 2, except by freak chance. However a value of d much lower than 2 leaves you with

two choices. One is to assume that H

is true and that the low value of d has arisen as a matter of

chance. The other is that the disturbance term is subject to positive autocorrelation. As usual, the

choice is made by establishing a critical value d

crit

below which d would not sink, say, more than 5

percent of the time. If d were below d

crit

, you would then reject H

at the 5 percent significance level.

The critical value of d at any significance level depends, as you might expect, on the number of

explanatory variables in the regression equation and the number of observations in the sample.

Unfortunately, it also depends on the particular values taken by the explanatory variables. Thus it is

not possible to construct a table giving the exact critical values for all possible samples, as one can

with the t test and the F test, but it is possible to calculate upper and lower limits for the critical value

of d. Those for positive autocorrelation are usually denoted d

and d

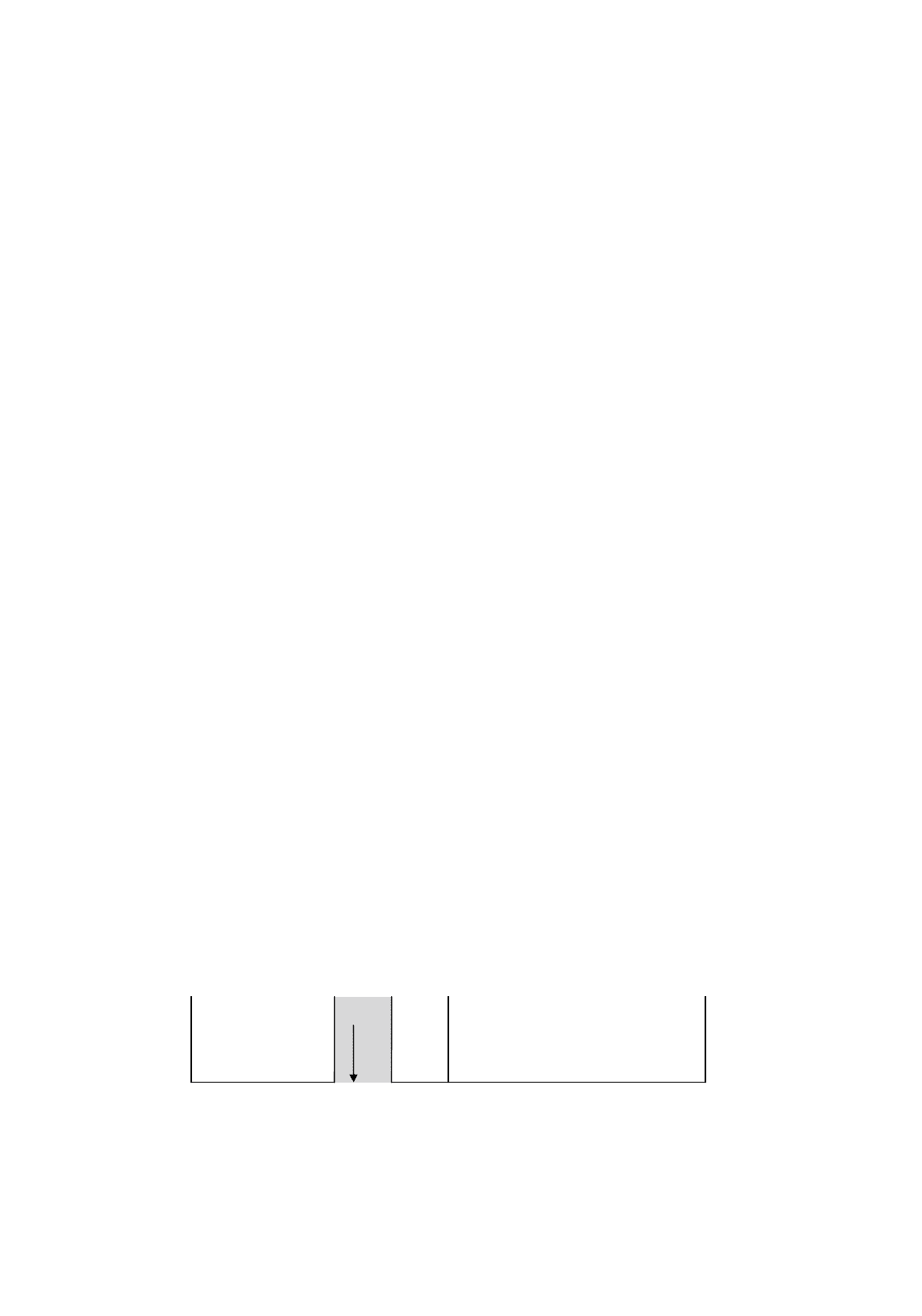
Figure 13.3 represents the situation schematically, with the arrow indicating the critical level of d,

which will be denoted d

crit

. If you knew the exact value of d

crit

, you could compare the d statistic for

your regression with it. If d > d

cri

, you would fail to reject the null hypothesis of no autocorrelation.

If d < d

crit

, you would reject the null hypothesis and conclude that there is evidence of positive

autocorrelation.

However, all you know is that d

crit

lies somewhere between d

and d

. This leaves you with three

possible outcomes for the test.

1. d is less than d

. In this case, it must be lower than d

crit

, so you would reject the null

hypothesis and conclude that positive autocorrelation is present.

2. d is greater than d

. In this case, d must be greater than d

crit

, so you would fail to reject the

null hypothesis.

3. d lies between d

and d

. In this case, d might be greater or less than d

crit

. You do not know

which, so you cannot tell whether you should reject or not reject the null hypothesis.

In cases (1) and (2), the Durbin–Watson test gives you a definite answer, but in case (3) you are left in

a zone of indecision, and there is nothing that you can do about it.

Table A.5 at the end of this text gives d

and d

cross-classified by number of explanatory

variables and number of observations, for the 5 percent and 1 percent significance levels, for the case

Figure 13.3.

Durbin–Watson test for autocorrelation, showing the zone of

indeterminacy in the case of suspected positive autocorrelation

240

crit

AUTOCORRELATION

Figure 13.4.

Durbin–Watson test for autocorrelation, showing the zone of

indeterminacy in the case of suspected negative autocorrelation

of positive AR(1) autocorrelation. You can see the zone of indecision between d

and d

decreases as

the sample size increases. Testing for negative autocorrelation follows a similar pattern, with the zone

containing the critical value symmetrically located to the right of 2. Since negative autocorrelation is

relatively uncommon, you are expected to calculate the limits of the zone yourself from the figures for

positive autocorrelation for the corresponding number of explanatory variables and number of

observations. This is easy enough to do. As is illustrated in Figure 13.4, 4 – d

gives the lower limit,

below which you fail to reject the null hypothesis of no autocorrelation, and 4 – d

gives the upper

one, above which you conclude that there is evidence of negative autocorrelation.

It should be noted that a low d statistic does not necessarily mean that the model is subject to

AR(1) autocorrelation. It will be low whenever there is a pattern of positive residuals tending to be

followed by positive ones and negative ones by negative ones, and this could be caused by model

misspecification. In particular, it is often caused by the omission of an important variable from the

model, and it may happen if the regression is using an inappropriate mathematical function. We will

discuss these cases of apparent autocorrelation below.

Example

The output shown below gives the result of a logarithmic regression of housing services on disposable

personal income and the relative price of housing services. The Durbin–Watson statistic is 0.85. For

= 0 and H

≠

0, d

is 1.15 for a 1 percent significance test (2 explanatory variables, 36

observations). We would therefore reject H

============================================================

Dependent Variable: LGHOUS

Method: Least Squares

Sample: 1959 1994

Included observations: 36

============================================================

Variable CoefficientStd. Errort-Statistic Prob.

============================================================

C -2.032685 0.322726 -6.298478 0.0000

LGDPI 1.132248 0.008705 130.0650 0.0000

LGPRHOUS -0.227634 0.065841 -3.457323 0.0015

============================================================

R-squared 0.998154 Mean dependent var 5.996930

Adjusted R-squared 0.998042 S.D. dependent var 0.377702

S.E. of regression 0.016714 Akaike info criter-5.265522

Sum squared resid 0.009218 Schwarz criterion -5.133562

Log likelihood 97.77939 F-statistic 8920.496

Durbin-Watson stat 0.846451 Prob(F-statistic) 0.000000

============================================================

20 4

crit

AUTOCORRELATION

Exercises

13.1

Examine the Durbin–Watson statistic for the logarithmic demand function that you fitted in

Exercise 12.4. Is there evidence of autocorrelation? If so, what are the implications for the

statistical tests you performed?

13.2

If your regression application allows you to graph or print the residuals from a regression, do

this in the case of your logarithmic demand function. Does an inspection of the residuals

corroborate the presence (or absence) of autocorrelation indicated by the Durbin–Watson

statistic?

13.3 What Can You Do about Autocorrelation?

We will consider only the case of AR(1) autocorrelation. It has received the most attention in the

literature because it is intuitively plausible and there is seldom sufficient evidence to make it

worthwhile considering more complicated models. If the observations are taken quarterly or monthly,

however, other models may be more suitable, but we will not investigate them here.

AR(1) autocorrelation can be eliminated by a simple manipulation of the model. Suppose that the

model is

+ u

(13.7)

with u

generated by the process

–1

, (13.8)

If we lag equation (13.7) by one time period and multiply by

, we have

–1

(13.9)

Now subtract (13.9) from (13.7):

–

–1

(1–

) +

–

–1

+ u

–

–1

(13.10)

Hence

(1–

) +

–1

–

–1

, (13.11)

The model is now free from autocorrelation because the disturbance term has been reduced to the

innovation

. In the case of the more general multiple regression model

+ ... +

+ u

, (13.12)

AUTOCORRELATION

with u

following an AR(1) process, we follow the same procedure. We lag the equation and multiply

it by

–1

+ ... +

–1

+ u

–1

, (13.13)

Subtracting (13.13) from (13.12) and rearranging, we again derive a model free from autocorrelation:

(1–

) +

–1

–

–1

+ ... +

–

–1

, (13.14)

Note that the model incorporates the nonlinear restriction that the coefficient of the lagged value

of each X variable is equal to minus the product of the coefficients of its current value and Y

–1

. This

means that you should not use OLS to fit it. If you did, there would be no guarantee that the

coefficients would conform to the theoretical restrictions. Thus one has to use some nonlinear

estimation procedure instead. The most common are nonlinear least squares, on the lines discussed in

Chapter 5, and maximum-likelihood estimation.

Example

The output below shows the result of a logarithmic regression of housing services on disposable

personal income and the relative price of housing services, using the nonlinear specification

represented by equation (13.14). The model is

LGHOUS

(1–

) +

LGHOUS

–1

LGDPI

–

LGDPI

–1

LGPRHOUS

–

LGPRHOUS

–1

. (13.15)

The nonlinear specification is reproduced as part of the regression output. C(1), C(2), C(3), and C(4)

are estimates of

, and

, respectively. The fitted equation is therefore

OUSHLG

= C(1)[1 – C(2)] + C(2)LGHOUS(–1) + C(3)LGDPI – C(2)C(3)LGDPI(–1)

+ C(4)LGPRHOUS – C(2)C(4)LGPRHOUS(–1) (13.16)

This equation is reproduced as part of the EViews output. You can see that the estimate of

is very

high indeed, 0.97, suggesting that there was very severe autocorrelation in the original specification.

The estimate of the income elasticity is much lower than in the OLS regression, but the estimate of the

price elasticity is much the same.

We have noted that most regression applications designed for time series analysis include the

Durbin–Watson statistic as a standard component of the output. In the same way, they usually have a

built-in option for fitting models where the disturbance term has an AR(1) specification, making it

unnecessary to use a nonlinear equation such as (13.16) to spell out the structure of the model. In the

case of EViews, adding AR(1) to the list of regressors converts the specification from OLS to that

appropriate for AR(1) autocorrelation. Early regression applications tended to use the Cochrane–

Orcutt iterative procedure, described in the box. It effectively enables the nonlinear AR(1) model to

be fitted using linear regression analysis, a major benefit when computers were still in their infancy

and nonlinear estimation was so time-consuming that it was avoided if possible. Now that nonlinear

regression is a standard feature of major regression applications, the Cochrane–Orcutt iterative