Dougherty С. Introduction to Econometrics, 3Ed

Подождите немного. Документ загружается.

MODELS USING TIME SERIES DATA

aggregate data for the whole of the United States and that kind of interpretation is not sensible.

It is common to hypothesize that a constant elasticity function of the type

vPRELHOUSDPIHOUS

ββ

(12.2)

is mathematically more appropriate for demand functions. Linearizing it by taking logarithms, one

obtains

LGHOUS =

' +

LGDPI +

LGPRHOUS + u, (12.3)

where LGHOUS, LGDPI and LGPRHOUS are the (natural) logarithms of HOUS, DPI and

PRELHOUS, respectively, u is the natural logarithm of the disturbance term v,

' is the logarithm of

, and

and

are income and price elasticities. The regression result is now as shown:

=============================================================

Dependent Variable: LGHOUS

Method: Least Squares

Sample: 1959 1994

Included observations: 36

=============================================================

Variable Coefficient Std. Error t-Statistic Prob.

=============================================================

C -2.032685 0.322726 -6.298478 0.0000

LGDPI 1.132248 0.008705 130.0650 0.0000

LGPRHOUS -0.227634 0.065841 -3.457323 0.0015

=============================================================

R-squared 0.998154 Mean dependent var 5.996930

Adjusted R-squared 0.998042 S.D. dependent var 0.377702

S.E. of regression 0.016714 Akaike info criter -8.103399

Sum squared resid 0.009218 Schwarz criterion -7.971439

Log likelihood 97.77939 F-statistic 8920.496

Durbin-Watson stat 0.846451 Prob(F-statistic) 0.000000

=============================================================

The coefficients of LGDPI and LGPRHOUS are direct estimates of the income and price

elasticities. Is 1.13 a plausible income elasticity? Probably. It is conventional to classify consumer

expenditure into normal goods and inferior goods, types of expenditure whose income elasticities are

positive and negative, respectively, and to subdivide normal goods into necessities and luxuries, types

of expenditure whose income elasticities are less than 1 and greater than 1. Housing is obviously a

necessity, so you might expect the elasticity to be positive but less than 1. However it also has a

luxury element, since people spend more on better quality housing as their income rises. Overall the

elasticity seems to work out at about 1, so the present estimate seems reasonable.

Exercises

12.1

The results of linear and logarithmic regressions of consumer expenditure on food, FOOD, on

DPI and a relative price index series for food, PRELFOOD, using the Demand Functions data

set, are summarized below. Provide an economic interpretation of the coefficients and perform

appropriate statistical tests.

MODELS USING TIME SERIES DATA

ODOF

= 232.6 + 0.089 DPI – 0.534 PRELFOOD R

= 0.989

(31.9) (0.002) (0.332)

OODFLG

= 2.66 + 0.61 LGDPI – 0.30 LGPRFOOD R

= 0.993

(0.28) (0.01) (0.07)

12.2

Download the Demand Functions data set and associated manuals from the website. You should

choose, or be assigned by your instructor, one category of expenditure, and it may be helpful to

simplify the data set by deleting the expenditure and price variables relating to the other

categories.

Construct a relative price index series for your category as indicated in Section 1 of

the Demand Functions Regression Exercises manual. Plot the series and try to explain why it

has changed over the time period.

12.3

Regress your category of expenditure on DPI and the relative price index series constructed in

Exercise 12.1. Give an economic interpretation of the regression coefficients and perform

appropriate statistical tests.

12.4

Regress the logarithm of expenditure on your category on LGDPI and the logarithm of the

relative price series. Give an economic interpretation of the regression coefficients and perform

appropriate statistical tests.

12.5*

Perform a Box–Cox test to determine whether there is a significant difference in the fit of the

linear and logarithmic regressions for your category of expenditure.

12.6

Sometimes a time trend is included in a regression as an explanatory variable, acting as a proxy

for some gradual change not associated with income or price. Changing tastes might be an

example. However, in the present case the addition of a time trend might give rise to a problem

of multicollinearity because it will be highly correlated with the income series and perhaps also

the price series. Calculate the correlations between the TIME variable in the data set, LGDPI,

and the logarithm of expenditure on your category. Regress the logarithm of expenditure on

your category on LGDPI, the logarithm of the relative price series, and TIME (not the logarithm

of TIME). Provide an interpretation of the regression coefficients, perform appropriate

statistical tests, and compare the regression results with those of the same regression without

TIME.

12.2 Dynamic Models

Next, we will introduce some simple dynamics. One might suppose that some types of consumer

expenditure are largely determined by current income and price, but this is not so for a category such

as housing that is subject to substantial inertia. We will consider specifications in which expenditure

on housing depends on lagged values of income and price. A variable X lagged one time period has

values that are simply the previous values of X, and it is conventionally referred to as X(–1).

Generalizing, a variable lagged s time periods has the X values s periods previously, and is denoted

X(–s). Major regression applications adopt this convention and for these there is no need to define

lagged variables separately. Table 12.1 shows the data for LGDPI, LGDPI(–1) and LGDPI(–2).

MODELS USING TIME SERIES DATA

ABLE

12.1

Current and Lagged Values of the

Logarithm of Disposable Personal Income

Year LGDPI LGDPI(–1) LGDPI(–2)

1959 5.2750 - -

1960 5.3259 5.2750 -

1961 5.3720 5.3259 5.2750

1962 5.4267 5.3720 5.3259

1963 5.4719 5.4267 5.3720

1964 5.5175 5.4719 5.4267

1965 5.5706 5.5175 5.4719

...... ...... ...... ......

1987 6.3689 6.3377 6.3119

1988 6.3984 6.3689 6.3377

1989 6.4210 6.3984 6.3689

1990 6.4413 6.4210 6.3984

1991 6.4539 6.4413 6.4210

1992 6.4720 6.4539 6.4413

`1993 6.4846 6.4720 6.4539

1994 6.5046 6.4846 6.4720

ABLE

12.2

Alternative Dynamic Specifications, Expenditure on Housing Services

Variable (1) (2) (3) (4) (5)

LGDPI 1.13

(0.01)

0.38

(0.15)

0.33

(0.14)

LGDPI(–1)

1.10

(0.01)

0.73

(0.15)

0.28

(0.21)

LGDPI(–2)

1.07

(0.01)

0.48

(0.15)

LGPRHOUS –0.23

(0.07)

–0.19

(0.08)

–0.13

(0.19)

LGPRHOUS(–1)

–0.20

(0.06)

0.14

(0.08)

0.25

(0.33)

LGPRHOUS(–2)

–0.19

(0.06)

–0.33

(0.19)

0.998 0.999 0.998 0.999 0.999

MODELS USING TIME SERIES DATA

Note that obviously there is a very high correlation between LGDPI, LGDPI(–1) and LGDPI(–2), and

this is going to cause problems.

The first column of Table 12.2 presents the results of a logarithmic regression using current

income and price. The second and third columns show the results of regressing expenditure on

housing on income and price lagged one and two time periods, respectively. It is reasonable to

hypothesize that expenditure on a category of consumer expenditure might depend on both current and

lagged income and price. The fourth column shows the results of a regression using current income

and price and the same variables lagged one time period. The fifth column adds the same variables

lagged two time periods, as well.

The first three regressions are almost identical. This is because LGDPI, LGDPI(–1) and

LGDPI(–2) are very highly correlated. The last two regressions display the classic symptoms of

multicollinearity. The point estimates are unstable and the standard errors become much larger when

current and lagged values of income and price are included as regressors. For a type of expenditure

like housing, where one might expect long lags, this is clearly not a constructive approach to

determining the lag structure.

A common solution to the problem of multicollinearity is to hypothesize that the dynamic process

has a parsimonious lag structure, that is, a lag structure that can be characterized with few parameters.

One of the most popular lag structures is the Koyck distribution, which assumes that the coefficients

of the explanatory variables have geometrically declining weights. We will look at two such models,

the adaptive expectations model and the partial adjustment model.

Exercises

12.7

Give an economic interpretation of the coefficients of LGDPI, LGDPI(–1), and LGDPI(–2), in

column 5 of Table 12.2.

12.8

To allow for the possibility that expenditure on your category is partly subject to a one-period

lag, regress the logarithm of expenditure on your commodity on LGDPI, the logarithm of your

relative price series, and those two variables lagged one period. Repeat the experiment adding

LGDPI(–2) and the logarithm of the price series lagged two periods. Compare the regression

results, paying attention to the changes in the regression coefficients and their standard errors.

12.3 The Adaptive Expectations Model

The modeling of expectations is frequently an important and difficult task of the applied

economist using time series data. This is especially true in macroeconomics, in that investment,

saving, and the demand for assets are all sensitive to expectations about the future. Unfortunately,

there is no satisfactory way of measuring expectations directly for macroeconomic purposes.

Consequently, macroeconomic models tend not to give particularly accurate forecasts, and this make

economic management difficult.

As a makeshift solution, some models use an indirect technique known as the adaptive

expectations process. This involves a simple learning process in which, in each time period, the actual

value of the variable is compared with the value that had been expected. If the actual value is greater,

MODELS USING TIME SERIES DATA

the expected value is adjusted upwards for the next period. If it is lower, the expected value is

adjusted downwards. The size of the adjustment is hypothesized to be proportional to the discrepancy

between the actual and expected value.

If X is the variable in question, and

X is the value expected in time period t given the

information available at time period t–1,

)(

XXXX

−=−

≤

1) (12.4)

This can be rewritten

XXX )1(

λλ

−+=

,(0

≤

1) (12.5)

which states that the expected value of X in the next time period is a weighted average of the actual

value of X in the current time period and the value that had been expected. The larger the value of

the quicker the expected value adjusts to previous actual outcomes.

For example, suppose that you hypothesize that a dependent variable, Y

, is related to the expected

value of the explanatory variable, X, in year t+1,

uXY

++=

121

. (12.6)

(12.6) expresses Y

in terms of

, which is unobservable and must somehow be replaced by

observable variables, that is, by actual current and lagged values of X, and perhaps lagged values of Y.

We start by substituting for

using (12.5):

(

)

ttt

uXX

uXXY

+−++=

)1(

221

λλ

(12.7)

Of course we still have unobservable variable

X as an explanatory variable, but if (12.5) is true

for time period t, it is also true for time period t–1:

XXX

)1(

−−

−+=

λλ

. (12.8)

Substituting for

X in (12.7), we now have

tttt

uXXXY

+−+−++=

−−

21221

)1()1(

λλ

(12.9)

After lagging and substituting s times, the expression becomes

tttt

uXX

XXXY

+−+−+

+−+−++=

+−+−

−

−−

121

21221

)1()1(

...)1()1(

λλ

(12.10)

MODELS USING TIME SERIES DATA

Now it is reasonable to suppose that

lies between 0 and 1, in which case (1 –

) will also lie between

0 and 1. Thus (1 –

)

becomes progressively smaller as

increases. Eventually there will be a point

where the term

)1(

+−

−

is so small that it can be neglected and we have a model in which all

the variables are observable.

A lag structure with geometrically-declining weights, such as this one, is described as having a

Koyck distribution. As can be seen from (12.10), it is highly parsimonious in terms of its

parameterization, requiring only one parameter more than the static version. Since it is nonlinear in

the parameters, OLS should not be used to fit it, for two reasons. First, multicollinearity would almost

certainly make the estimates of the coefficients so erratic that they would be worthless – it is precisely

this problem that caused us to search for another way of specifying a lag structure. Second, the point

estimates of the coefficients would yield conflicting estimates of the parameters. For example,

suppose that the fitted relationship began

= 101 + 0.60

+ 0.45

–1

+ 0.20

–2

+ ... (12.11)

Relating the theoretical coefficients of the current and lagged values of

in (12.10) to the estimates in

(12.11), one has

= 0.60,

(1 –

) = 0.45, and

(1 –

)

= 0.20. From the first two you could infer

that

was equal to 2.40 and

was equal to 0.25 – but these values would conflict with the third

equation and indeed with the equations for all the remaining coefficients in the regression.

Instead, a nonlinear estimation technique should be used instead. Most major regression

applications have facilities for performing nonlinear regressions built into them. If your application

does not, you could fit the model using a grid search. It is worth describing this technique, despite the

fact that it is obsolete, because it makes it clear that the problem of multicollinearity has been solved.

We rewrite (12.10) as two equations:

(12.12)

(1 –

)

–1

(1 –

)

–2

(1 –

)

–3

... (12.13)

The values of

depend of course on the value of

. You construct ten versions of the

variable

using the following values for

: 0.1, 0.2, 0.3, ..., 1.0 and fit (12.12) with each of them. The version

with the lowest residual sum of squares is by definition the least squares solution. Note that the

regressions involve a regression of

on the different versions of

in a simple regression equation and

so the problem of multicollinearity has been completely eliminated.

Table 12.3 shows the parameter estimates and residual sums of squares for a grid search where

the dependent variable was the logarithm of housing services and the explanatory variables were the

logarithms of

DPI

and the relative price series for housing. Eight lagged values were used. You can

see that the optimal value of

is between 0.4 and 0.5, and that the income elasticity is about 1.13 and

the price elasticity about –0.32. If we had wanted a more precise estimate of

, we could have

continued the grid search with steps of 0.01 over the range from 0.4 to 0.5. Note that the implicit

income coefficient for

–8

(1 –

)

, was about 1.13×0.5

= 0.0022. The corresponding price

coefficient was even smaller. Hence in this case eight lags were more than sufficient.

MODELS USING TIME SERIES DATA

ABLE

12.3

Logarithmic Regression of Expenditure on Housing Services on

Disposable Personal Income and a Relative Price Index, Assuming

an Adaptive Expectations Model, Fitted Using a Grid Search

s.e.(

)

s.e.(

)

RSS

0.1 1.67 0.01 –0.35 0.07 0.001636

0.2 1.22 0.01 –0.28 0.04 0.001245

0.3 1.13 0.01 –0.28 0.03 0.000918

0.4 1.12 0.01 –0.30 0.03 0.000710

0.5 1.13 0.01 –0.32 0.03 0.000666

0.6 1.15 0.01 –0.34 0.03 0.000803

0.7 1.16 0.01 –0.36 0.03 0.001109

0.8 1.17 0.01 –0.38 0.04 0.001561

0.9 1.17 0.01 –0.39 0.04 0.002137

1.0 1.18 0.01 –0.40 0.05 0.002823

Dynamics in the Adaptive Expectations Model

As you can see from (12.10),

, the current value of

, has coefficient

in the equation for

. This

is the short-run or impact effect of

. At time

, the terms involving lagged values of

are

already determined and hence effectively form part of the intercept in the short-run relationship.

However we can also derive a long-run relationship between

and

by seeing how the equilibrium

value of

would be related to the equilibrium value of

, if equilibrium were ever achieved. Denoting

equilibrium

and

, respectively, in equilibrium

and

XXXX

ttt

====

−−

...

. Substituting into (12.10), one has

XXXY

2221

...])1()1([

...)1()1(

λλλλλ

λλ

+−+−++=

(12.14)

To see the last step, write

(1 –

) +

(1 –

)

... (12.15)

Then

(1 –

)

(1 –

)

(1 –

)

(1 –

)

... (12.16)

Subtracting (12.16) from (12.15),

MODELS USING TIME SERIES DATA

S – (1 –

)S =

(12.17)

and hence S is equal to 1. Thus the long-run effect of X on Y is given by

An alternative way of exploring the dynamics of an adaptive expectations model is to perform

what is known as a Koyck transformation. This allows us to express the dependent variable in terms

of a finite number of observable variables: the current values of the explanatory variable(s) and the

dependent variable itself, lagged one time period. We start again with the original equations and

combine them to obtain (12.20):

uXY

++=

121

(12.18)

XXX )1(

λλ

−+=

(12.19)

(

)

ttt

uXX

uXXY

+−++=

)1(

221

λλ

(12.20)

Now if (12.18) is true for time t, it is also true for time t–1:

1211

−−

++=

uXY

(12.21)

Hence

1112

−−

−−=

uYX

(12.22)

Substituting this into (12.20), we now have

1211

11121

)1()1(

))(1(

−−

−−++−+=

+−−−++=

tttt

ttttt

uuXY

uuYXY

λλ

(12.23)

As before the short-run coefficient of X is

, the effective intercept for the relationship being

+ (1 –

–1

at time t. In equilibrium, the relationship implies

XYY

λλ

)1(

+−+=

(12.24)

and so

(12.25)

Hence again we obtain the result that

gives the long-run effect of X on Y.

We will investigate the relationship between the short-run and long-run dynamics graphically.

We will suppose, for convenience, that

is positive and that X increases with time, and we will

neglect the effect of the disturbance term. At time t, Y

is given by (12.23). Y

–1

has already been

determined, so the term (1 –

–1

is fixed. The equation thus gives the short-run relationship between

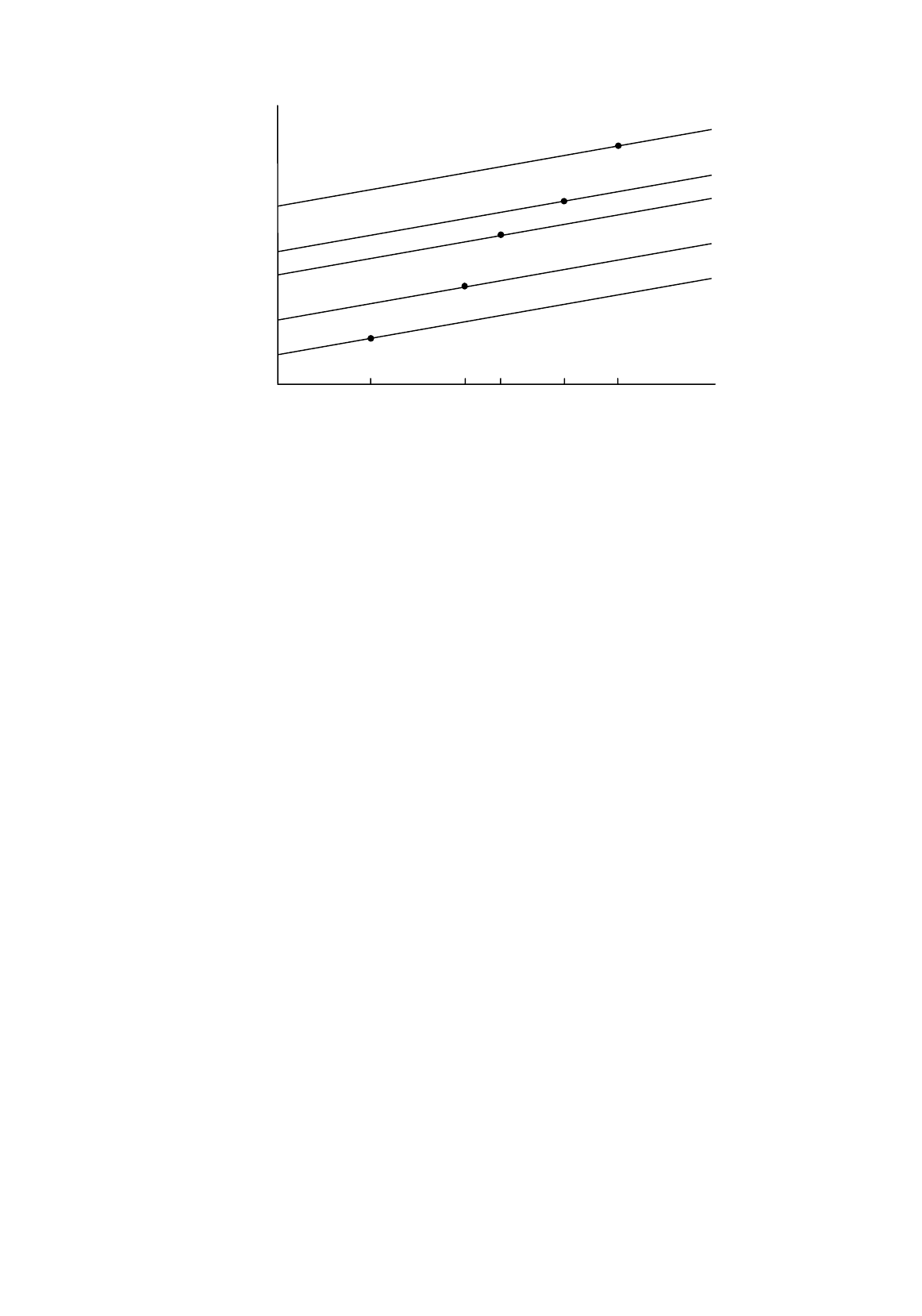
MODELS USING TIME SERIES DATA

Figure 12.2.

Short-run and long-run dynamics in the adaptive expectations model

and X

. [

+ (1 –

–1

] is effectively the intercept and

is the slope coefficient. When we

come to time t+1, Y

is given by

+ (1 –

(12.26)

and the effective intercept is now [

+ (1 –

]. Since X is increasing, Y is increasing, so the

intercept is larger than that for Y

and the short-run relationship has shifted upwards. The slope is the

same as before,

. Thus two factors are responsible for the growth of Y: the direct effect of the

increase in X, and the gradual upward shift of the short-run relationship. Figure 12.2 shows the

outcomes for time t as far as time t+4. You can see that the long-run relationship is steeper than the

short-run one.

Example: Friedman’s Permanent Income Hypothesis

Without doubt the most celebrated application of the adaptive expectations model is Friedman’s use of

it when fitting an aggregate consumption function using time series data. In the early years after the

Second World War, econometricians working with macroeconomic data were puzzled by the fact that

the long-run average propensity to consume seemed to be roughly constant, despite the marginal

propensity to consume being much lower. A model in which current consumption was a function of

current income could not explain this phenomenon and was therefore clearly too simplistic. Several

more sophisticated models that could explain this apparent contradiction were developed, notably

Friedman's Permanent Income Hypothesis, Brown's Habit Persistence Model (discussed in the next

section), Duesenberry's Relative Income Hypothesis and the Modigliani–Ando–Brumberg Life Cycle

Model.

Under the Permanent Income Hypothesis, permanent consumption,

C , is proportional to

permanent income,

Y :

αλ

+ (1–

)

–1

αλ

(

1–

)

αλ

(

1–

)

αλ

+ (1–

)

αλ

+ (1–

)

MODELS USING TIME SERIES DATA

(12.27)

Actual consumption,

, and actual income,

, also contain transitory components,

and

respectively:

CCC

(12.28)

YYY

(12.29)

It is assumed, at least as a first approximation, that the transitory components of consumption and

income have expected value 0 and are distributed independently of their permanent counterparts and

of each other. Substituting for

in (12.27) using (12.28) one has

CYC

(12.30)

We thus obtain a relationship between actual consumption and permanent income in which

plays

the role of a disturbance term, previously lacking in the model.

Earlier, when we discussed the permanent income hypothesis in the context of cross-section data,

the observations related to households. When Friedman fitted the model, he actually used aggregate

time series data. To solve the problem that permanent income is unobservable, he hypothesized that it

was subject to an adaptive expectations process in which the notion of permanent income was updated

by a proportion of the difference between actual income and the previous period’s permanent income:

)(

YYYY

−−

−=−

(12.31)

Hence permanent income at time

is a weighted average of actual income at time

and permanent

income at time

–1:

YYY

)1(

−

−+=

λλ

(12.32)

Friedman used (12.32) to relate permanent income to current and lagged values of income. Of

course it cannot be used directly to measure permanent income in year

because we do not know

and we have no way of measuring

−

. We can solve the second difficulty by noting that, if (12.32)

holds for time

, it also holds for time

–1:

YYY

211

)1(

−−−

−+=

λλ

(12.33)

Substituting this into (12.28), we obtain

ttt

YYYY

)1()1(

−−

−+−+=

λλλλ

(12.34)