Dougherty С. Introduction to Econometrics, 3Ed

Подождите немного. Документ загружается.

MODELS USING TIME SERIES DATA

This includes the unmeasurable term

−

, but we can deal with it by lagging (12.28) two periods

and substituting, thus obtaining

in terms of

–1

–2

and

−

. Continuing this process

indefinitely, we can write

as a weighted sum of current and past measured income:

...)1()1()1(

+−+−+−+=

−−−

tttt

YYYYY

λλλλλλλ

(12.35)

Provided that

lies between 0 and 1, a reasonable assumption, (1 –

)

is a decreasing function of

and eventually the weights attached to the lagged values of

become so small that they can be

neglected.

This still leaves us with the problem of estimating

. Friedman’s solution was to use a grid

search, calculating the permanent income time series for a range of values of

between 0 and 1, and

regressing consumption on each permanent income series. He then chose that value of

that produced

the series for

that gave him the best fit. Effectively, of course, he was fitting the nonlinear model

(1 −

)

–1

(1 −

)

–2

+ ...+

(12.36)

The dynamic properties of the model are as illustrated in Figure 12.1. Mathematically they are

best analyzed by performing the Koyck transformation on the model. This could be done on the lines

of equations (12.21) – (12.23) above, or by lagging (12.36) one period and multiplying through by (1 –

(1 –

)

–1

(1 –

)

–1

(1 −

)

–2

(1 −

)

–3

+ ...+ (1 –

)

–1

(12.37)

Subtracting (12.37) from (12.36), one has

– (1 –

)

–1

– (1 –

)

–1

(12.38)

and so

+ (1 –

)

–1

– (1 –

)

–1

(12.39)

The short-run marginal propensity to consume is

and the long run propensity is

. Since

less than 1, the model is able to reconcile a low short-run marginal propensity to consume with a

higher long-run average propensity. The dynamics of the model are as shown in abstract in Figure

12.2.

Exercise

12.9

* The output below shows the result of fitting the model

LGFOOD

LGDPI

(1 –

)

LGDPI

(–1)

(1 –

)

LGDPI

(–2) +

LGPRFOOD

MODELS USING TIME SERIES DATA

using the data on expenditure on food in the Demand Functions data set. LGFOOD and

LGPRFOOD are the logarithms of expenditure on food and the relative price index series for

food. C(1), C(2), C(3), and C(4) are estimates of

, and

, respectively. Explain how

the regression equation could be interpreted as an adaptive expectations model and discuss the

dynamics implicit in it, both short-run and long-run. Should the specification have included

further lagged values of LGDPI?

============================================================

Dependent Variable: LGFOOD

Method: Least Squares

Sample(adjusted): 1961 1994

Included observations: 34 after adjusting endpoints

Convergence achieved after 848 iterations

LGFOOD=C(1)+C(2)*C(3)*LGDPI+C(2)*C(3)*(1-C(3))*LGDPI(-1)+C(2)

*C(3)*(1-C(3))*(1-C(3))*LGDPI(-2)+C(4)*LGPRFOOD

============================================================

CoefficientStd. Errort-Statistic Prob.

============================================================

C(1) 2.666180 0.316754 8.417199 0.0000

C(2) 0.607542 0.013005 46.71599 0.0000

C(3) 0.863231 0.346065 2.494419 0.0184

C(4) -0.303995 0.072186 -4.211252 0.0002

============================================================

R-squared 0.991081 Mean dependent var 6.132194

Adjusted R-squared 0.990190 S.D. dependent var 0.179564

S.E. of regression 0.017785 Akaike info criter-5.110752

Sum squared resid 0.009490 Schwarz criterion -4.931180

Log likelihood 90.88279 F-statistic 1111.264

Durbin-Watson stat 0.604156 Prob(F-statistic) 0.000000

============================================================

12.4 The Partial Adjustment Model

In the partial adjustment model it is assumed that the behavioral equation determines the desired

(or "target") value,

Y , of the dependent variable, rather than the actual value, Y

ttt

uXY

++=

(12.40)

It is then assumed that the actual increase in the dependent variable, Y

– Y

–1

, is proportional to the

discrepancy between the desired value and the previous value,

Y – Y

–1

)(

−−

−=−

tttt

YYYY

≤

1) (12.41)

This may be rewritten

)1(

−

−+=

ttt

YYY

λλ

(12.42)

so it can be seen that Y

is a weighted average of the current desired value and the previous actual

value. The higher is the value of

, the more rapid is the adjustment process. If

is equal to 1, Y

MODELS USING TIME SERIES DATA

equal to

and there is full adjustment in one period. At the other extreme, if

is equal to 0,

does

not adjust at all.

Substituting for

from the target relationship, one obtains

ttt

tttt

uYX

YuXY

+−++=

−+++=

−

121

)1(

)1()(

λλ

(12.43)

Thus the parameters

, and

of the behavioral model can be estimated by regressing

and

–1

. The model relates

to the current value of

and the lagged value of itself, and so has the same

structure as the Koyck-transformed version of the adaptive expectations model. It follows that its

dynamics are exactly the same. The coefficient of

–1

yields an estimate of (1 –

) and hence of

, the

speed of adjustment. The coefficient of

gives the short-run effect of

and also, when divided

by the estimate of

, the long-run effect.

Example: Brown’s Habit-Persistence Model of Aggregate Consumption

The first attempts by econometricians to fit an aggregate consumption function naturally used the

simple static model

(12.44)

With estimates of

well below 1, this model implied that the average propensity to consume should

fall. Nevertheless long-run data showed no tendency for this to happen. Consequently

macroeconomists started looking for more elaborate models that could reconcile these apparently

contradictory facts. Friedman’s Permanent Income Hypothesis was one such model. Another was

Brown’s Habit-Persistence Model (Brown, 1952). In this model, desired consumption

was related

to wage income,

, and nonwage income,

tttt

uANWWC

++++=

321

(12.45)

Brown used aggregate data for Canada for the years 1926–1949, omitting the war years 1942–

1945,

being a dummy variable equal to 0 for the pre-war period and 1 for the post-war period. The

division of income into wage income and nonwage income follows the observation of Michael Kalecki

that the marginal propensity to consume out of wage income was likely to be much higher than that

out of nonwage income, for two reasons. First, nonwage income tends to be received by relatively

rich households with higher savings rates than poorer ones. Second, in a market economy, much

nonwage income originates as company profits, and companies normally pass on only part of their

profits as dividends to shareholders, retaining the remainder for investment in the business.

Because households are slow to adapt their spending patterns in response to changes in income,

Brown hypothesized a partial adjustment process for actual consumption:

)(

−−

−=−

tttt

CCCC

(12.46)

MODELS USING TIME SERIES DATA

From this one obtains current consumption as the weighted average of desired consumption and

consumption in the previous time period:

)1(

−

−+=

ttt

CCC

λλ

(12.47)

Substituting for

from (12.45), one then has an equation in observable variables:

tttt

ttttt

uACNWW

CuANWWC

λλλλ

++−+++=

−+++++=

−

1321

)1(

)1()(

(12.48)

Fitting the model with a simultaneous equations technique, Brown obtained (

statistics in

parentheses):

= 0.90 +0.61

+ 0.28

+ 0.22

–1

+ 0.69

(12.49)

(4.8) (7.4) (4.2) (2.8) (4.8)

The variables were all measured in Canadian $ billion at constant prices of the 1935–1939 period.

From the regression one obtains short-run marginal propensities to consume of 0.61 and 0.28 for wage

income and nonwage income, respectively. The coefficient of

–1

indicates that 0.78 of the

discrepancy between desired and actual income is eliminated in one year. Dividing the short-run

marginal propensities by the speed of adjustment, one obtains long-run propensities to consume of

0.78 and 0.36 for wage income and nonwage income, respectively.

Comparison of the Friedman and Brown Models

Despite the fact that their theoretical frameworks are completely different, one concerned with the

future and expectations, the other concerned with the past and inertia, the Friedman model, in its

Koyck-transformed form (12.39), and the habit-persistence model (12.48) are virtually identical. They

both incorporate short-run and long-run propensities to consume and a speed of adjustment. The only

difference in the variable specification is that the Brown model divides income into wage income and

nonwage income. This is a useful refinement that should be applied to Friedman model as well.

Indeed it is now a standard feature of empirical models. The Friedman model does not have an

intercept, but that is a minor empirical detail. The disturbance term in the Friedman model is different

from that in the Brown model, and its structure may cause problems, but as will be seen in the next

chapter, that is likewise not an important difference. This is an example of the problem of

observationally-equivalent theories, where two or more theories can be used to fit the same data set in

the same way and there is no possibility of discriminating between them.

Exercises

12.10

Expenditure on housing services,

HOUS

, was regressed on

DPI

, the relative price index for

housing,

PRELHOUS

, and the lagged value of

HOUS

(–1), for the period 1959–1994

MODELS USING TIME SERIES DATA

for the United States using the Demand Functions data set. The regression was repeated in

logarithmic form, LGHOUS being regressed on LGDPI, LGPRHOUS, and LGHOUS(–1), with

the results summarized below. Give an interpretation of the regression coefficients, paying

attention to the dynamics implicit in the model.

USOH

= 19.24 + 0.05 DPI – 0.28 PRELHOUS + 0.69 HOUS(–1) R

=0.9998

(10.14) (0.01) (0.10) (0.04)

OUSHLG

= –0.39 + 0.32 LGDPI – 0.07 LGPRHOUS + 0.70 LGHOUS(–1) R

=0.9998

(0.15) (0.05) (0.02) (0.05)

12.11

Perform regressions parallel to those reported in Exercise 12.10 for your category of

expenditure in the Demand Functions data set. Give an interpretation of the regression

coefficients, paying attention to the dynamics implicit in the model.

12.12*

How would you test Kalecki's assertion concerning the coefficients of wage and nonwage

income, if you had access to Brown's data set?

12.13*

In his classic study Distributed Lags and Investment Analysis (1954), Koyck investigated the

relationship between investment in railcars and the volume of freight carried on the U.S.

railroads using data for the period 1884–1939. Assuming that the desired stock of railcars in

year t depended on the volume of freight in year t–1 and year t–2 and a time trend, and

assuming that investment in railcars was subject to a partial adjustment process, he fitted the

following regression equation using OLS (standard errors and constant term not reported):

= 0.077 F

–1

+ 0.017F

–2

– 0.0033t – 0.110K

–1

= 0.85

Provide an interpretation of the equation and describe the dynamic process implied by it.

(Note: It is best to substitute K

– K

–1

for I

in the regression and treat it as a dynamic

relationship determining K

12.5 Prediction

Suppose that you have fitted a model

+ u

(12.50)

to a sample of T time series observations (t = 1 , …, T):

= b

+ b

(12.51)

Given any post-sample period value of X, say X

, you are now in a position to predict the

corresponding value of Y:

MODELS USING TIME SERIES DATA

(12.52)

There are two reasons why such predictions may be important to you. First, you may be one of

those econometricians whose business it is to peer into the economic future. Some econometricians

are concerned with teasing out economic relationships with the aim of improving our understanding of

how the economy works, but for others this is only a means to the more practical objective of trying to

anticipate what will happen. In most countries macroeconomic forecasting has a particularly high

profile, teams of econometricians being employed by the Ministry of Finance or other branches of

government, private financial institutions, universities and research institutes, and their predictions are

actively used for framing public policy, for commenting on it, or for business purposes. When they

are published in the press, they typically attract far more attention than most other forms of economic

analysis, both on account of their subject matter and because, unlike most other forms of economic

analysis, they are easily understood by the ordinary citizen. Even the most innumerate and

nontechnically minded person can have a good understanding of what is meant by estimates of the

future levels of unemployment, inflation, etc.

There is, however, a second use of econometric prediction, one that has made it of concern to

econometricians, irrespective of whether they are involved in forecasting. It provides a method of

evaluating the robustness of a regression model that is more searching than the diagnostic statistics

that have been used so far.

Before we go any further, we will have to clarify what we mean by

prediction

. Unfortunately, in

the econometric literature this term can have several slightly different meanings, according to the

status of

in (12.52). We will differentiate between ex-post predictions and forecasts. This

classification corresponds to what seems to be the most common usage, but the terminology is not

standard.

Ex-Post Predictions

We will describe

as an ex-post prediction if

is known. How can this be the case? In

general, econometricians make use of all available data, to maximize the sample size and hence

minimize the population variances of their estimators, so

will simply be the most recent recorded

value of

available at the time of running the regression. Nevertheless, there are two circumstances

when

will be known as well: when you have waited

or more periods after running the

regression, and when you have deliberately terminated the sample period early so that you have a few

of the most recent observations left over. The reason for doing this, as we shall see in the next section,

is to enable you to evaluate the predictive accuracy of the model without having to wait.

For example, referring again to the price inflation/wage inflation model of equation (3.39),

suppose that we had fitted the equation

= 1.0 + 0.80

(12.53)

during the sample period, where

and

are the percentage annual rates of price inflation and wage

inflation, respectively, and suppose that we know that the rate of wage inflation was 6 percent in some

prediction period year. Then we can say that the ex-post prediction of the rate of wage inflation is 5.8

percent. We should, of course, be able to compare it immediately with the actual rate of price inflation

MODELS USING TIME SERIES DATA

for that year, and hence we can evaluate the prediction error, which is just the difference between

actual outcome and the predicted value. In general, if Y

is the actual outcome, and

the

predicted value, the forecast error is defined as f

where

= Y

–

(12.54)

Why is there a prediction error? For two reasons. First,

has been calculated using the

parameter estimates, b

and b

, instead of the true values. And second,

cannot take account of

the disturbance term u

, which is a component of Y

. In the discussion that follows, we shall

assume that the data include T+P observations on the variables, the first T (the sample period) being

used to fit the regression and the last P (the prediction period or prediction interval) being used to

check predictive accuracy.

Example

Suppose that when we fitted the demand function for housing using the Demand Functions data set,

we had only used the first 32 observations in the sample, that is, the observations for 1959–90,

reserving the last four observations for checking predictions. The fitted equation for 1959–90 is

(standard errors in parentheses):

OUSHLG

= –1.96 +1.13LGDPI – 0.24LGPRHOUS R

= 0.998 (12.55)

(0.39) (0.01) (0.08)

The predicted values of LGHOUS for the period 1991–94, using the equation and the actual values of

disposable personal income and the relative price of housing services for those years, are shown in

Table 12.4, together with the actual outcomes and the prediction errors. The predictions, like the basic

data, are in logarithmic form. For convenience, Table 12.4 also shows the absolute values, derived

from the logarithmic values, expressed in $ billion at 1992 prices.

We can see that in this case the predicted value of expenditure on housing services is roughly 2

percent below the actual outcome in 1991, and very close in the remaining three years. Is this

predictive performance satisfactory? We shall see in the next section.

ABLE

12.4

Predicted and Actual Expenditure on Housing Services, 1991–1994

Logarithms Absolute equivalent

Year LGHOUS

OUSHLG

Error HOUS

USOH

Error

1991 6.4539 6.4734 0.0166 635.2 624.8 10.4

1992 6.4720 6.4697 0.0023 646.8 645.3 1.5

1993 6.4846 6.4820 0.0026 655.0 653.3 1.7

1994 6.5046 6.5073 –0.0027 668.2 670.0 –1.8

MODELS USING TIME SERIES DATA

Forecasts

If you are willing to predict a particular value of Y

, without knowing the actual value of X

, you

are said to be making a forecast, at least in the terminology of this text. The macroeconomic

divinations published in the press are usually forecasts in this sense. Policymakers, and indeed the

general public, are not much interested in two-handed economists (ones who say "on the one hand this

… but if … then on the other hand that …"). They want the best possible single-point estimates,

perhaps with some indication of the likely margin of error, often not even that. Forecasts are less

accurate than predictions because they are subject to an additional source of error, the error in the

prediction of X

. Obviously, those making forecasts normally attempt to minimize the additional

error by modeling the behavior of X as carefully as possible, in some instances constructing a separate

model for it, in others bringing the equation determining Y and the equation determining X together,

usually with other relationships as well, in a simultaneous equations model of the type discussed in

Chapter 10.

Properties of Least Squares Predictors

In the discussion that follows, we will be concerned with predictions rather than forecasts, the reason

being that we are in a position to make statements about the properties of the regression coefficients

and the disturbance term, but not about X if its values are not known. First, there is some good news.

If Y

is generated by the same process as the sample period values of Y (that is, according to equation

(12.50) with u

conforming to the Gauss–Markov conditions), and if we make our prediction

using equation (12.52), the prediction error f

will have mean 0 and minimum variance.

The first property is easily demonstrated:

)()()(

)()(

)

()()(

2121

=−−+=

−−++=

+−++=

−=

+++

pTpT

pTpTpT

bEXbEuEX

XbbEuXE

YEYEfE

(12.56)

since E(b

) =

, E(b

) =

, and E(u

) = 0. We will not attempt to prove the minimum variance

property (for a proof, see Johnston and Dinardo, 1997). Both of these properties carry over to the

general case of multiple regression analysis.

In the simple regression case, the population variance of f

is given by

)(Var

)(

σσ





















−

++=

(12.57)

where

and Var(X) are the sample period mean and variance of X. Unsurprisingly, this implies that,

the farther is the value of X from its sample mean, the larger will be the population variance of the

MODELS USING TIME SERIES DATA

prediction error. It also implies, again unsurprisingly, that, the larger is the sample, the smaller will be

the population variance of the prediction error, with a lower limit of

. As the sample becomes

large,

and

will tend to their true values (provided that the Gauss–Markov conditions hold), so the

only source of error in the prediction will be

, and by definition this has population variance

Confidence Intervals for Predictions

We can obtain the standard error of the prediction error by replacing

in (12.57) by

and taking

the square root. Then (

–

)/standard error follows a

distribution with the number of degrees

of freedom when fitting the equation in the sample period. Hence we can derive a confidence interval

for the actual outcome,

–

crit

s.e. <

crit

s.e. (12.58)

where

crit

is the critical level of

, given the significance level selected and the number of degrees of

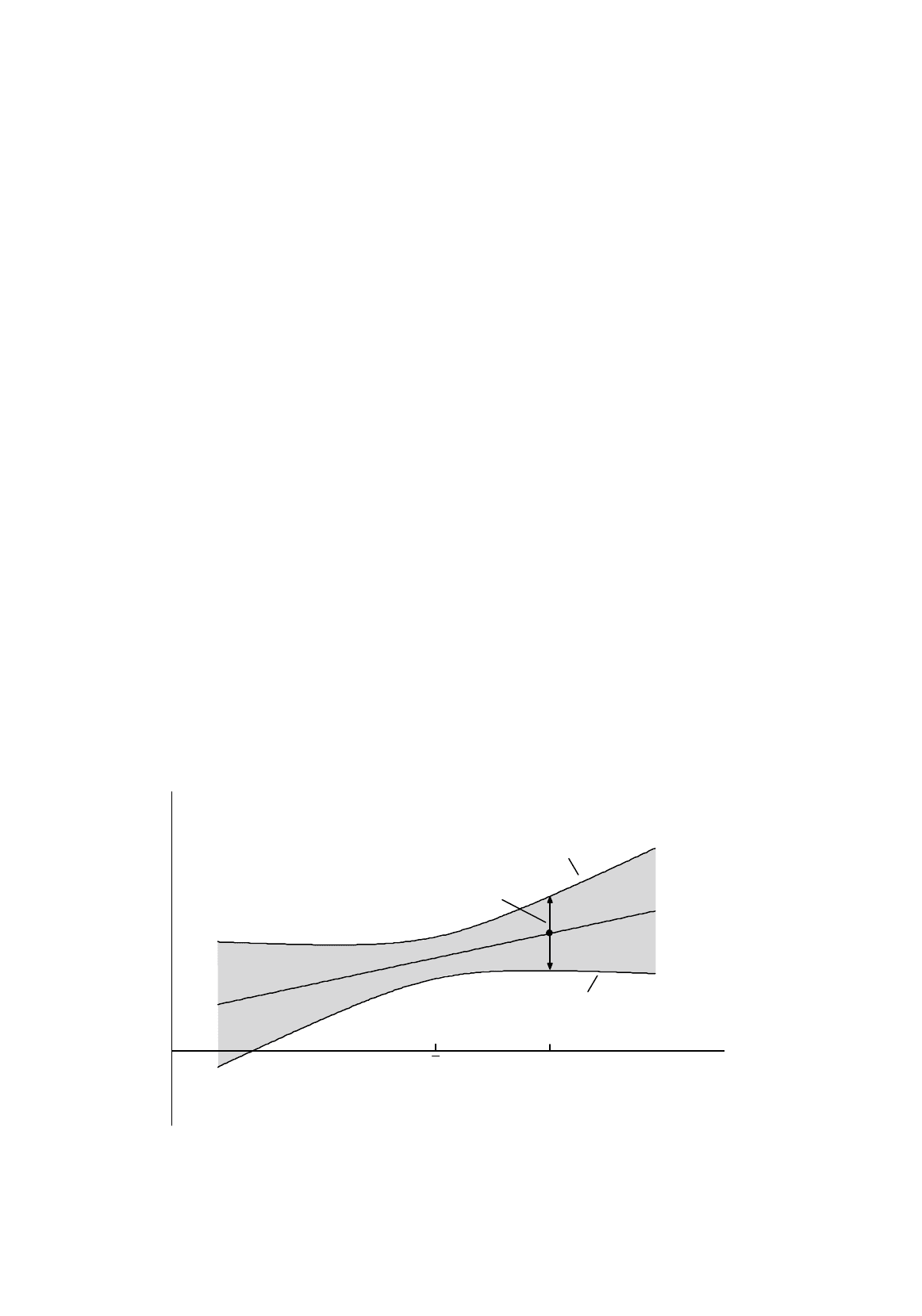
freedom, and s.e. is the standard error of the prediction. Figure 12.3 depicts in general terms the

relationship between the confidence interval for prediction and the value of the explanatory variable.

In multiple regressions, the counterpart to (12.57) is much more complicated and is best handled

with matrix algebra. Fortunately, there is a simple trick that you can use to get the computer to

calculate the standard errors for you. Let the sample period be denoted 1, …,

and the prediction

period

+1, …,

. You run the regression for the sample and prediction periods combined, adding

a (different) dummy variable to each of the prediction period observations. This means adding to the

model a set of dummy variables

, …,

, where

is defined to be 0 for every observation

except observation

, for which it is 1. It can be shown (Salkever, 1976; Dufour, 1980) that the

Figure 12.3.

Confidence interval for a projection

lower limit of

confidence interval

upper limit of confidence interval

confidence interval

for

pTpT

XbbY

MODELS USING TIME SERIES DATA

estimates of the nondummy coefficients and their standard errors will be exactly the same as in the

regression confined to the sample period only. The computer uses the dummy variables to obtain a

perfect fit in each observation in the prediction period, and it does this by setting the coefficient of the

dummy variable equal to the prediction error as defined above. The standard error of this coefficient

is equal to the standard error of the prediction error.

Example

============================================================

Dependent Variable: LGHOUS

Method: Least Squares

Sample: 1959 1994

Included observations: 36

============================================================

Variable CoefficientStd. Errort-Statistic Prob.

============================================================

C -1.959273 0.388319 -5.045522 0.0000

LGDPI 1.129984 0.010942 103.2737 0.0000

LGPRHOUS -0.239828 0.075874 -3.160890 0.0037

D1991 0.016561 0.018991 0.872042 0.3903

D1992 0.002325 0.019033 0.122150 0.9036

D1993 0.002604 0.019109 0.136289 0.8925

D1994 -0.002732 0.019268 -0.141796 0.8882

============================================================

R-squared 0.998206 Mean dependent var 5.996930

Adjusted R-squared 0.997835 S.D. dependent var 0.377702

S.E. of regression 0.017576 Akaike info criter-5.071925

Sum squared resid 0.008958 Schwarz criterion -4.764019

Log likelihood 98.29465 F-statistic 2689.096

Durbin-Watson stat 0.838021 Prob(F-statistic) 0.000000

============================================================

The output shows the result of a logarithmic regression of housing services on income and relative

price with dummy variables for the years 1991 – 1994. The coefficients of the dummy variables give

the forecast errors presented in Table 12.4. The predicted logarithm of expenditure on housing

services in 1991 in Table 12.4 was 6.4374. From the output we see that the standard error of the

prediction error for that year was 0.0190. With 29 degrees of freedom, the critical value of t at the 5

percent significance level is 2.045, so we obtain the following 95 percent confidence interval for the

prediction for that year:

6.4374 – 2.045

0.0190 < Y < 6.4374 + 2.045

0.0190 (12.59)

that is,

6.3985 < Y < 6.4763 (12.60)

The confidence interval does include the actual outcome, 6.4539, and thus, for that year at least, the

prediction was satisfactory. The same is true for the other years in the prediction period.