Доспехов Б.А. Методика полевого опыта
Подождите немного. Документ загружается.


/ 2 3 4 5 . 6
,
Рис.
13. Расположение делянок различной формы в одном повторении:
1—2
—
удлиненные и прямоугольные в один ярус; 3
—
прямоугольные в два яруса; 4 —
квадратные в четыре яруса; 5
—
прямоугольные в два яруса, ступенчато; 6
—
квадратные-
в четыре яруса, ступенчато.
Отсутствие контроля возможного закономерного варьирова-
ния плодородия почвы здесь компенсируется увеличением числа
степеней свободы для ошибки. Увеличение числа степеней сво-
боды для ошибки при закладке опытов с небольшим числом де-
лянок важно для оценки существенности разности средних по.
критерию F.
Для опыта, представленного на рисунке 11, число степеней
свободы для оценки ошибки равно 9
(N—Z=12—3
=
9),
тогда'
как в методе рендомизированных повторений оно равно толь-
ко 6: (1—1)
(/г—1)
= (3—1) (4—1)=6. Чтобы 'считать разности
существенными, в первом случае значение критерия Р должно
превышать 4,26, а во втором
—
5,14.
Если есть основания считать одну часть опытного участка,
более плодородной, чем другую, а также при желании исклю-
чить возможность случайного размещения всех делянок с одним
вариантом вместе, но все же сохранить больше степеней сво-
боды для ошибки, можно разделить участок на блоки, вклю-
чающие 2—3 полных набора всех вариантов. Для примера, изо-
браженного на рисунке 12 опыт можно разделить на два блока
по шесть делянок в каждом и в каждом блоке выделить по две
делянки для размещения каждого из трех изучаемых вариан-
тов.
Варианты по делянкам в каждом блоке должны разме-
щаться случайно (рис. 12).
При выделении двух блоков рендомизация ограничивается»,
но здесь теряется только одн-а степень свободы для ошибки
(Ь—1
=
2—1
=
1)
и критерий F увеличивается незначительно, с-
4,26 до 4,46, т. е. потеря чувствительности в сравнении с полной
рендомизацией невелика.
По мере увеличения делянок в опыте расстояние между
сравниваемыми вариантами возрастает, а в связи с увеличением-
расстояния возрастают различия и в плодородии почвы, что сни-
жает эффективность метода неорганизованных повторений, и
необходимо использовать метод организованных повторений.
Метод рендомизированных повторений. Это наиболее рас-
пространенный в мировой практике опытного дела метод раз-
мещения вариантов по делянкам полевого опыта. В каждом-
повторении варианты распределяются по делянкам в случайном-
порядке. Важно, чтобы внутри каждого повторения почва была
по возможности более однородной, а форма повторения при-
69
2
ц
I
1
5
3 J
5
Ж
2 4
1
4
2
Ш
3
/
•
s\z
5
Ш
1
3
!
!
J
8
9
S
8
4
В
St
/
•
J
5i
1
7
5
2
J
5
St
1
St
1
2
9
7
St
1
4
5
2
2
Si
1
7
3
3
7
St
1
9
9
8
4
5
Б
В
8
St
1
19
St
15
\w
1
r
m
~~т~-r~r
-
J группа
\St,
1S\15\20
IB
I
! Г
3 группа
1 1 1
17\20\Щ19
ii—1
2 группа
If
f
2
I3_\_7
групп
St
1
В
tz
a
4-
I
/71/0
1
18
14
2
9
St
3 \15
14
\JL
8
"1 1 1
2 гвуппа
,St ,
id
7
13\S
/группа
St
1
,17
1
5)3 В
12
ID
3 группа
19 IB
3 группа.
20
17
IB 18
St
15
19
18
14
8
13
20
St
7
4
W
/ группа •
St.
i | J 5
i r т
2 группа
\8
3
1 1
14\I2\I1
В
9
1 группа
5 Б 2
2 группа
1
9\I3
1
I2\1l
4
8
2
St
7
St
1
w
я
ж
ж
л
ш
ш
1
2
3
Ч
5
4
2 5 3
1
5 3
2
1
ц.
1
2 5
3
4
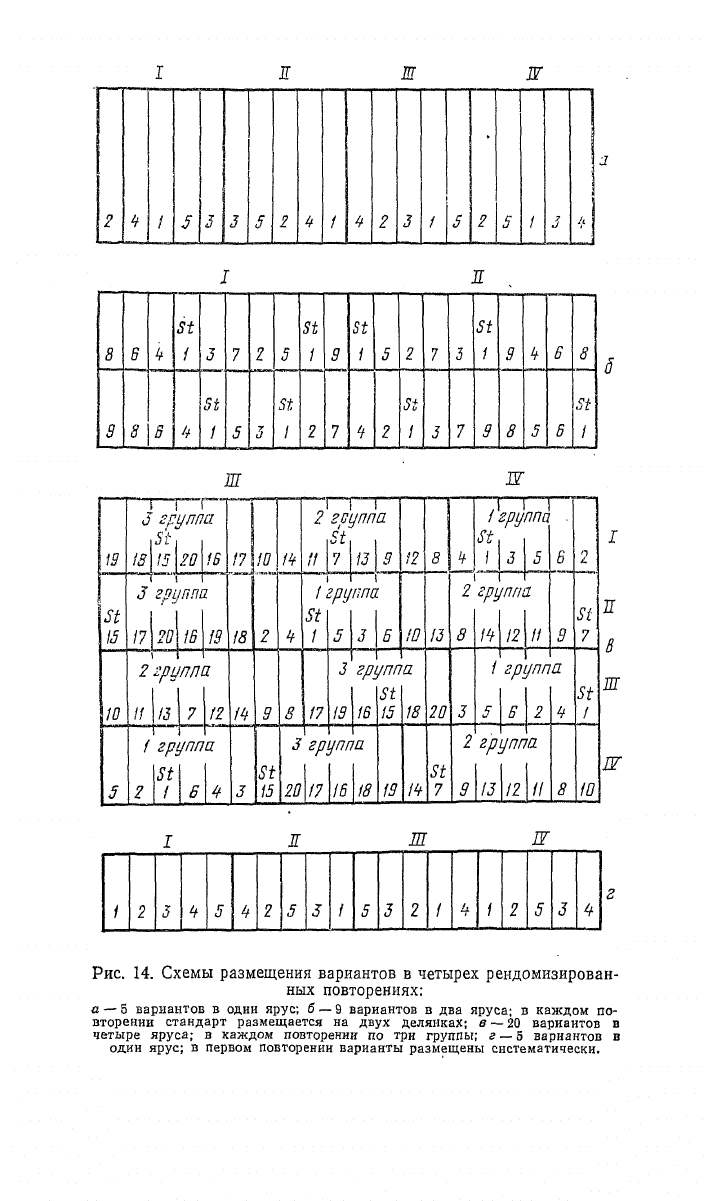
Рис.
14. Схемы размещения вариантов в четырех рендомизирован-
ных повторениях:
а — 5 вариантов в одни ярус; 6
— 9
вариантов в два яруса; в каждом по-
вторении стандарт размещается на двух делянках; в
— 20
вариантов в
четыре яруса; в каждом повторении по три группы; г
—
5 вариантов в
один ярус; в первом повторении варианты размещены систематически.

ближалась к квадрату. В этом случае при любом пространст-
венном расположении делянок они будут лучше сравнимы
между собой.
В зависимости от технических условий проведения опыта
повторения подразделяются на делянки удлиненной, прямо-
угольной или квадратной формы.
Делянки располагают в один, два или много рядов (яру-
сов).
В ряде случаев повторение может иметь неправильную
ступенчатую форму (рис. 13).
Чаще всего повторения располагают на поле компактно в
один, два или больше ярусов. Однако, когда земельный участок
недостаточно выравнен, повторения можно разбросать, рассеять
по полю поодиночке или группами.
Число изучаемых вариантов в методе случайных повторений
зависит от выравненное™ земельного участка и размера опыт-
ных делянок. Большинство исследователей указывают, что не
следует иметь более 15—20 вариантов. Когда число вариантов
превышает 8—10, целесообразно в каждом повторении иметь
две или более делянок стандарта (контроля), что позволяет
значительно повысить точность сравнения опытных вариантов
со стандартом (рис. 14).
Часто, особенно в длинных схемах, целесообразно объеди-
нить варианты (сорта) внутри повторения в однородные груп-
ны,
например, по морфологическим или другим признакам (вы-
сокорослость, скороспелость и т.п.). Порядок расположения
групп в каждом повторении и вариантов внутри групп опре-
деляется рендомизацией. При этом в каждой группе может
быть свой стандарт.
Иногда, например, в демонстрационных и учебных целях в
одном повторении желательно расположить варианты в каком-
то определенном порядке, т. е. систематически. Это частичное
отступление от строгой рендомизации может быть допустимо,
ибо оно не является грубым нарушением, так как всегда имеет-
ся вероятность, особенно при небольшом числе вариантов, слу-
чайно получить в одном из повторений последовательное раз-
мещение вариантов (рис.
14,
г).
Латинский квадрат и прямоугольник. Размещение опытных
делянок методом латинского- квадрата позволяет в значитель-
ной степени сэлиминировать, устранить влияние систематичес-
кого изменения плодородия почвы опытного участка на резуль-
таты опыта по двум взаимно перпендикулярным направлени-
ям.
Для этого земельный участок квадратной или прямоуголь-
ной формы разбивают в горизонтальном и вертикальном на-
правлениях на столько рядов и столбцов, сколько вариантов
в опыте. Любой ряд и любой столбец включают полный на-
бор изучаемых вариантов, которые размещаются на делянках
квадратной или прямоугольной формы. При удлиненной форме
делянок латинский квадрат не имеет особых преимуществ пе-
ред методом рендомизированных повторений.
5—724
65

Столбцы
Л Ш Ш
ч
ш
Рис.
15.
опыта
5
г
1
*
3
1
5
3
2
4
А
3
5
1
2
2
t
4
J
5
J
и
2
5
i
Схема
латинским
5X5.
размещения
квадратом
Расположение опыта латинским
квадратом требует, чтобы число
повторений обязательно было рав-
но числу вариантов. Поэтому об-
щее число делянок в опыте всегда
будет равно квадрату числа вари-
антов схемы. При четырех вариан-
тах в опыте будет 4X4=16 деля-
нок, при пяти 5X5=25, при шести
6X6 =
36
делянок и т.д. На площа-
ди их размещают рядами и столб-
цами. В каждом ряду и столбце
должен быть полный набор всех
вариантов, и, следовательно, ни
один из вариантов не повторяется
дважды ни в строке, ни в столбце.
Кроме этих двух ограничений, ва-
рианты размещаются внутри столбцов и рядов случайно, по
таблице случайных чисел.
Например, для пяти вариантов, обозначенных цифрами 1, 2,
3,
4, 5, расположение их в рядах и столбцах может быть таким,
как на рисунке 15.
Здесь каждая строка и столбец содержат все варианты и ни
в строке, ни в столбце одноименные варианты не повторяются
дважды. Такое расположение позволяет охватить изменение
плодородия почвы в двух взаимно перпендикулярных направ-
лениях и математической обработкой устранить его влияние на
результаты опыта, повысить точность эксперимента. Недоста-
ток латинского квадрата
—
требование равенства числа повто-
рений числу вариантов. В связи с этим увеличение числа ва-
риантов ведет к громоздким опытам и предусматривает боль-
шую повторность, чем что обычно требуется. Поэтому в прак-
тике опытной работы наибольшее распространение получили
квадраты 5x5, 6X6, 7X7. Нерационально закладывать квад-
раты с числом вариантов меньше четырех. В этом случае стан-
дартная ошибка опирается на небольшое число наблюдений и
становится неустойчивой базой для оценки существенности раз-
личий между вариантами.
На рисунке 16 даны некоторые схемы размещения полевых
опытов латинским квадратом 4'Х4, 5x5, 6X6, 7X7 и 8x8.
Если есть основания считать, что варьирование неконтроли-
руемых условий эксперимента может быть не только по двум
перпендикулярным направлениям, но и по диагоналям, то целе-
сообразно сблокировать варианты не только по строчкам и ко-
лонкам, но и по блокам, расположенным по диагоналям.
При 7—8 и более вариантах постановка опытов латинским
квадратом становится затруднительно, и, чтобы, не прибегая
к излишней повторности, использовать преимущества латинско-
го квадрата, целесообразно закладывать опыты латинским пря-
66

4 Варианта (4 *4)
3
1
2
4
I
2
h
3
...
2
k
3
1
„
4
3
1
2
f
2
4
3
3
4
2
1
4
3
1
2
2
f
3
4
5
Вариантов
{5^5)
2
4
5
1
3
J
2
1
4
5
5
3
4
2
1
i
5
2
3
4
4
1
3
5
2
3
4
2
1
5
5
i
4
3
2
f
2
5
4
J
4
5
3
2
t
2
3
/
3
4
7 Вариантов (7*7)
2
3
f
7
2
5
В
4
В
3
2
4
7
/
5
1
Б
3
5
4
7
2
2
5
4
В
1
3
7
7
4
6
I
2
5
3
5
2
i
7
3
4
В
4
7
5
3
В
2
i
1
5
В
2
7
3
4
4
2
5
1
В
7
3
3
7
1
4
2
В
5
5
1
3
6
4
2
7
2
3
4
7
/
5
В
В
4
7
5
3
1
2
7
В
2
3
5
4
/
Вариантов
(8><8)
4
J
2
(
2
1
3
4
/
2
4
3
3
4
/
2
5
2
4
3
/
2
4
J
/
5
1
3
5
2
4
4
/
2
5
3
3
5
i
4
2
5
/
В
2
4
J
/
3
4
5
В
2
1
4
5
2
3
1
В
В
2
/
4
3
5
3
В
5
1
2
4
2
4
3
В
5
1
В
Вариантов
Б
/
4
3
2
ZJ
4
5
2
1
В
3
/
4
В
5
3
2
3
В
5
2
4
/
(В
5
2
3
4
/
В
*S)
2
3
I
В
5
4
/
3
В
4
2
5
2
4
5
3
1
В
и
В
2
3
5
4
/
'
4
5
1
6
3
2
5
I
4
2
В
3
3
в
2
t
5
4
4
5
3
2
1
7
В
7
f
В
3
5
4
2
Б
4
5
7
2
3
1
3
Б
7
1
4
2
5
5
7
2
4
В
I
3
2
3
1
В
7
5
4
/
2
4
5
3
В
7
3
5
2
7
i
4
8
Б
¥
2
1
5
8
В
3
7
1
Б
7
8
3
5
4
2
Б
1
5
4
7
8
1
3
5
8
¥
3
Б
2
7
1
8
7
В
2
5
3
1
4
2
3
8
1
4
7
Б
5
7
Ц
3
6
г
1
5
8
2
4
3
8
7
1
5
В
5
7
В
4
2
3
8
1
В
8
1
7
4
5
2
3
4
3
8
Б
1
2
7
5
8
2
5
/
Б
4
3
7
7
В
4
J
5
8
1
2
3
i
2
5
8
7
В
4
/
5"
7
2
3
6
4
8
4
/
5
7
2
8
В
3
2
В
8
1
7
3
5
4
8
5
7
В
4
/
3
2
7
4
3
8
В
5
2
1
}
7
В
4
3
2
8
S
S
2
4
3
8
В
1
7
3
8
2
5
1
7
4
В
Б
3
1
2
5
4
7
8
Рис.
16. Схемы размещения опытов с 4—8 вариантами латинским квадра-
том.

Столбцы
Ж
ж
ж
1
1
ж
k
1
12
3
9.
5
6
7
И
2
8
W
1
В
5
5
7
10
k
&
г
12
9
II
8
3
1
9
12
4
5
2
W
7
и
В
В
II
г
*
3
9
7
1
5
8
10
12
Рис.
17. Схема размещения опыта
с 12 вариантами латинским прямо-
угольником 4X4X3.
моуголышком. В этом случае
число вариантов должно быть
кратным числу повторностей.
Так, при трехкратной повтор-
ности этим методом можно
заложить опыт с 6, 9, 12, 18
и т. д. вариантами; при четы-
рехкратной—с 8, 12, 16, 24
и т. д. вариантами, при пяти-
кратной —- с 10, 15, 20, 25 ва-
риантами и т. д.
Число вариантов должно
делиться без остатка на число
повторностей. Частное от де-
ления дает число делянок, на
которое необходимо расще-
пить столбец соответствующе-
го латинского квадрата. На-
пример, при изучении 12 вариантов в четырехкратной повторно-
сти каждый столбец латинского квадрата 4X4 необходимо
расщепить в вертикальном или горизонтальном направлении
на три полосы (12:4=3). Такой метод закладки опыта носит
название латинского прямоугольника 4X4X3 (рис. 17). Произ-
ведение всех цифр (у нас 4X4X3=48) дает общее число деля-
нок в опыте, а произведение двух последних цифр 4X3=12—>
число вариантов.
Варианты по делянкам рендомизируют так, чтобы ряд и
столбец имели полный набор всех вариантов. Такое располо-
жение позволяет путем математической обработки устранить
влияние систематического варьирования плодородия почвы в
двух перпендикулярных направлениях и, следовательно, сни-
зить ошибку эксперимента. Некоторые схемы латинского пря-
моугольника для 15—20 вариантов даны на рисунке 18.
Метод расщепленных делянок. Метод расщепленных (слож-
ных) делянок используют преимущественно для закладки мно-
гофакторных опытов, когда в отношении одного какого-либо
фактора требуется получить точную информацию, а в отноше-
нии других факторов нет необходимости добиваться большой
точности.
Расщепленные делянки используют также в случаях, когда
необходимо в стационарном опыте ввести дополнительную
группу вариантов, сохранив все первоначальные варианты. Не-
редко постановка опыта методом расщепленных делянок дик-
туется техническими условиями проведения эксперимента.
Например, при испытании доз удобрений, гербицидов и сорто-
испытании на малых делянках можно объединить целые группы
таких делянок и на укрупненных площадках испытать различ-
ные предшественники или виды обработки почвы, которые тре-
буют более крупных делянок. Опыты, поставленные таким об-
68

I
л
ж
1
л
ж
15
Вариантов (3^3X5)
Л
ш
3
9
1
13
10
5
12
4
В
/4
8
15
И
7
2
2
13
8
1
14
7
5
3
4-
15
12
9
• В
и
10
7
5
14
9
6
12
4
1
3
10
15
13
8
2
11
18 Вариантов
{3*3*6)
12
4
13
2
14
/
9
16
17
5
18
IB
8
3
ff
7
ID
В
17
B\5
13
8
14
3
IB
7
15
12
4
10
2
9
1
If
18
14
6
8
17
9
3
4
/
10
11
5
2
IB
7
18
13
12
115
I
Ж
ш
R
7
8
2
15
I
9
В
11
1
12
5
10
IB
3
14
4
13
15
11
5
3
16
2
13
10
<B
L
и
1
4
9
12
ЧариантоВ (4>
Ш
В
7
8
14
2
12
6
11
4
3
15
8
14
1
IB
5
<4**t)
13
10
7
9
ft
9
3
2
W
8
IB
14
7
5
,13
12
4
10
15
1
В
I
Л
m
л
i
10
3
13
4
В
2
20
5
И
12
I
1
15
19
16
7
(4
9
8
18
17
9
8
IB
В
2
20 Вариантов (5*5
Л Ш
20
19
4
12
1
3
13
11
17
14
15
5
18
7
10
13
17
20
14
18
5
7
9
1
//
В
12
15
2
4
19
6
3
10
16
1В
2
12
15
19
*4)
Ш
4
1
6
20
8
18
14
7
9
13
(1
10
17
3
5
7
11
14
13
20
Ж
6
16
2
19
15,.
17
18
10
8
9
12
*
1
5
3
Рис.
18. Схемы размещения опытов с 15—20 вариантами методом
латинского прямоугольника.
разом, называют опытами с расщепленными делянками. Схема
расщепленных делянок —это эксперимент, в котором делянки
одного опыта используются как блоки для другого. Делянки
первого порядка (крупные делянки) делят, расщепляют в вер-
тикальном или горизонтальном направлении на делянки второ-
го порядка, а делянки второго порядка на более мелкие де-
лянки третьего порядка (рис. 19).
На рисунке 20 показана схема расположения двухфакторно-
го опыта 5X3 методом расщепленных делянок по изучению
пяти градаций способов обработки почвы А (а
и
а
2
, а
д
, а
4
, а
5
\
и трех градаций удобрений В (в,, в
2
, е
3
). Здесь делянки, на ко-
69

Рис.
19. Схема расщепления де-
лянки при постановке двухфактор-
иых /—2 и трехфакторных 3—4
опытов.
торых изучаются варианты об-
работки почвы, называемые
главными делянками или де-
лянками первого порядка,
расщепляют, делят на малые
субделянки, или делянки вто-
рого порядка, предназначен-
ные для вариантов удобрений.
На рисунке 21 представлена
схема размещения одного пов-
торения опыта 3X2X3 с трой-
ным расщеплением.
Варианты по главным де-
лянкам и субделянкам размещают методом рендомизации. Осо-
бенность их расположения заключается в том, что варианты
главных делянок рендомизируются самостоятельно по каждо-
му повторению, а варианты делянок второго и последующих
порядков рендомизируются каждый раз заново или для каждой
главной делянки или для целого повторения (рис. 22).
Смешивание. Рассмотренный метод расщепленных делянок
удобен при работе в поле, но он имеет один недостаток: в мно-
говариантных опытах с большими размерами повторений на-
чинают сильно проявляться неравноточность сравнения главных
эффектов и взаимодействий. Эффекты вариантов, размещенных
на субделянках, а также взаимодействия высших порядков оце-
ниваются обычно более точно, чем главные эффекты вариантов,
занимающих делянки первого порядка. Теория планирования
эксперимента рекомендует в этих случаях использовать метод
смешивания. Этот метод позволяет значительно повысить
точность сравнения главных эффектов в многофакторных
опытах с повышенным числом вариантов.
Метод смешивания предусматривает выделение внутри пов-
торений специально организованных блоков (неполных повто-
рений), включающих определенный набор вариантов схемы.
Сравнения внутри блоков более точны, чем между блоками, и
поэтому варианты группируют в блоки так, чтобы внутриблоко-
вые сравнения составляли наиболее существенную часть резуль-
а
3
а
ч
a, a
s
а
2
a
z
а, а
ч
% а
3
b
i\b
3
\b
2
1 1
1
I
ЬлЬ,\Ь
3
l 1
i
i
thrift
1 !
I l
h\k\h
1 1
1 1
b
3
\b
2
\b
t
1 1
1 1
a, a
s
a
fy
а
г
а
3
b
x
\b,\bf
I i
I 1
1 1
1 1
h\hfj
i
i
i
i
ъ
2
\ъ,\ъ
3
l l
\\b
3
\b,
1
1
n
1
1
b
f
\b
3
\b
2
i
l
i
i
bj\b
2
\b
3
1 1
1 1
b
2
\b,\b
3
1 1
1 1
Ь,\Ь
3
\Ъ
2
I
1
1 1
4 0-2 о-в
а
з
a
/
b
3
\b
2
\b,
i i
b
z
\bj\b,
1 1
1 1
1 1
b,\b
3
\b
2
1 1
1 1
1 \
b,\bj\b
2
1 1
1 1
1 1
b
2
\b
3
\b,
1 i
1 i
...,.L,
L...
Ш
ж
Рис.
20. Схема размещения двухфакторного опыта с 15 вариантами (5x3)
методом расщепленных делянок, ловторность четырехкратная.
70
ъ
4
ж
*/
татов опыта, а междублоко- а
г
а,
вые сравнения — менее суще-
ственную. Например, можно
пожертвовать взаимодействия-
ми высшего порядка, значимо-
сть которых маловероятна.
Таким образом, смешива-
нием называется такой способ
размещения вариантов, при
котором в каждом повторении
все комбинации вариантов
подразделяют на две или бо-
лее групп (блоков) так, что-
бы разности между группами
составляли взаимодействия
высшего порядка, представляющие меньший интерес, чем глав-
ные эффекты и взаимодействия между двумя факторами.
Взаимодействия высшего порядка при таком размещении опы-
та отождествляются, смешиваются с междублоковыми разли-
чиями, и, следовательно, экспериментатор жертвует сведения-
ми о таких взаимодействиях.
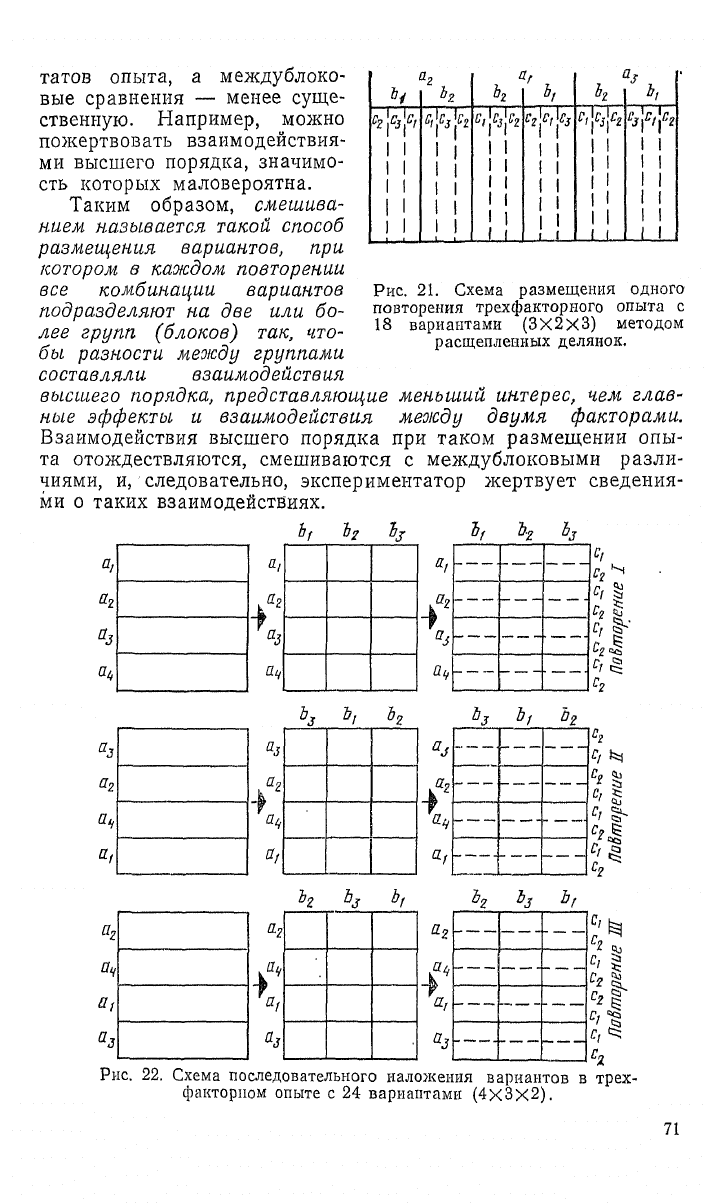
Рис.
21. Схема размещения одного
повторения трехфакториого опыта с
18 вариантами (3X2X3) методом
расщепленных делянок.
Ч
0-1
а
2
а
3
а^
b
f
h
h
a
i
k
2
~f
ц
h
r, ^
%
4
llif
a
t
Ьз h h
0^
a
a
h
D
2
a
H
4
p
У
*J
h
h
b,
fin
"-£
\"
f
0-1
а
з
h
—
—
h
.—
—
ь,
—
—
J'fe,
С,
Щ
Рис.
22.
Схема последовательного наложения вариантов
в
трех-
факторном опыте с 24 вариантами (4x3x2).
71

Глава 5
ПЛАНИРОВАНИЕ ПОЛЕВОГО ЭКСПЕРИМЕНТА
Научные исследования и разработки, осуществляемые мето-
дом полевого эксперимента, включают три основных этапа:
1) планирование; 2) проведение полевых опытов, наблюдений
и учетов; 3) обработку и обобщение полученных данных.
§ 1. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
Планирование
— это
определение задачи и объектов (расте-
ний) исследования, разработка схемы эксперимента, выбор зе-
мельного участка и оптимальной
структуры
полевого опыта.
Нетерпение и поспешность при планировании полевого опыта
редко приводят к быстрому и результативному завершению
экспериментальных исследований и разработок. Больше того,
поспешность может привести к существенным дефектам экспе-
римента— неправильному выбору градаций изучаемых факто-
ров,
контрольных и опытных вариантов, неоправданному уве-
личению объема работ, что сильно затрудняет техническое
проведение опыта, снижает достоверность данных и обходится
слишком дорого. Ошибки, допущенные при планировании,
нельзя исправить в последующем ни тщательным проведением
опытной работы, ни применением дорогостоящих инструмен-
тальных методов исследования и статистической обработки на
современных ЭВМ.
Период, предшествующий исследованию, включает: 1). выбор
темы, определение задачи и объекта исследования; 2) изучение
современного состояния вопроса; 3) выдвижение рабочей гипо-
тезы или ряда конкурирующих гипотез; 4) разработку схемы
и методики эксперимента. Эта часть работы, пожалуй, самая
трудная и ответственная.
Необходимо четко сформулировать цель исследования, по-
строить логическую модель изучаемого явления и правильно
выбрать стратегию, которая определяет методы и приемы ис-
следования.
Следующий этап планирования
—
изучение литературы по
избранной проблеме и выдвижение рабочей гипотезы или ряда
конкурирующих гипотез. Рабочая гипотеза служит отправным
пунктом для составления схемы или ряда схем будущих опытов,
и разработки программы исследования. В программе указывают
схемы опытов, основные элементы методики и техники экспери-
мента, наблюдения и учеты.
Сложным и ответственным этапом планирования является
разработка схемы и методики опыта, выбор полевых и лабора-
торных наблюдений (анализов) и учетов для оценки и объясне-
ния действия изучаемых факторов. Надежность результатов
эксперимента и соответствие их поставленной задаче зависят
72
