Долгов А.П., Лыкин А.В., Чебан В.М. Режимы электроэнергетических систем. Сборник задач
Подождите немного. Документ загружается.

11
Математическое ожидание суммы случайных величин равно
сумме их математических ожиданий
[
]
[
]
[
]
[ ]
1 1
,
.
n n
i i
i i
M X Y M X M Y
M X M X
= =
+ = +
=
∑ ∑
Математическое ожидание линейной функции случайных ве-
личин равно той же линейной функции от математических ожи-
даний этих величин
[ ]
1 1
.
n n
i i i i
i i
M a X b a M X b
= =
+ = +
∑ ∑
Математическое ожидание произведения двух случайных ве-
личин равно произведению их математических ожиданий плюс
ковариация между этими случайными величинами
[
]
[
]
[
]
(
)
cov .
M XY M X M Y XY
= +
Математическое ожидание произведения независимых слу-
чайных величин равно произведению их математических ожиданий
[ ]
1 1
.
n n
i i
i i
M X M X
= =
=
∏ ∏
Дисперсия суммы случайных величин равна сумме дисперсий
этих величин плюс удвоенная сумма ковариаций каждой из сла-
гаемых величин со всеми последующими
[
]
[
]
[
]
(
)
[ ]
( )
1 1
2cov ,
2 cov .
n n
i i i j
i i i j
D X Y D X D Y XY
D X D X X X
= = <
+ = + +
= +
∑ ∑ ∑
Дисперсия линейной функции случайных величин
[ ]
( )
2
1 1
2 cov .
n n
i i i i i j i j
i i i j
D a X b a D X a a X X
= = <
+ = +
∑ ∑ ∑
Дисперсия произведения двух независимых случайных величин

12
[
]
[
]
[
]
[
]
[
]
2 2
.
X Y
D XY D X D Y m D Y m D X
= + +
Упражнения
Упражнение 1
Случайная величина токовой нагрузки ветви электрической
сети трехфазного переменного тока подчиняется нормальному
закону распределения с параметрами M [I] = 200 А, σ
I
= 50 А.
Определить математическое ожидание, дисперсию и среднеквад-
ратическое отклонение потерь активной мощности в этой ветви,
если активное сопротивление ветви R = 2 Ом.
Вычисления
Потери мощности в сети являются функцией случайной вели-
чины тока нагрузки
2
3
P I R
∆ = .
Математическое ожидание потерь мощности
[ ] [ ]
( )
[ ]
{
}
(
)
2
2
3 3 2 200 2500 255
кВт
M P R M I D I∆ = + = ⋅ + = .
Дисперсия и среднеквадратическое отклонение потерь мощ-
ности
[ ]
( )
[ ]
( )
[ ]
( )
[ ]
{
}
( )
[ ]
2 2
2
2 2 2
3 2 4
9 4 2 2500 4 200 2500 14850
кВт ,
σ 14850 121,86 кВт.
P
D P R D I M I D I
D P
∆
∆ = + =
= ⋅ ⋅ + ⋅ ⋅ =
= ∆ = =
Упражнение 2
Две электрические системы объединены двухцепной электро-
передачей напряжением 220 кВ, длиной 250 км. Реактивное со-
противление двух параллельных линий 51,3 Ом. Напряжения по
концам электропередачи являются независимыми случайными
величинами соответственно с математическими ожиданиями
M[U
1
] = 219 кВ, M [U
2
] = 212 кВ и среднеквадратическими откло-
13
нениями σ
U1
= 7 кВ и σ
U2
= 6 кВ. Угол сдвига между векторами
напряжений U
1
и U
2
равен 30° и поддерживается неизменным.
Считая, что случайная величина передаваемой активной мощно-
сти распределена по нормальному закону, определить ее значе-
ние P
P
, вероятность превышения которого будет равна 0,0668.
Активным сопротивлением линий и их емкостной проводимо-
стью пренебречь.
Ответ: M [P] =452,5 МВт, D [P] = 373,4 МВт
2
, σ
P
= 19,3 МВт,
P
P
= 481,5 МВт.
Упражнение 3
От трансформаторной подстанции получают электроэнергию
четыре потребителя, нагрузки которых являются случайными ве-
личинами, подчиненные нормальным законам распределения с
параметрами
M[P
1
] = 600 кВт; σ
P1
= 400 кВт;
M[P
2
] = 400 кВт; σ
P2
= 300 кВт;
M[P
3
] = 500 кВт; σ
P3
= 250 кВт;
M[P
4
] = 700 кВт; σ
P4
= 500 кВт.
Корреляционная матрица (матрица коэффициентов корреля-
ции) для этих случайных величин
1 0,6 0,8 0,7
1 0,7 0,9
1 0,75
1
=
r .
Определить математическое ожидание и среднеквадратиче-
ское отклонение нагрузки подстанции и расчетную нагрузку под-
станции, вероятность превышения которой равна 0,0062.
Ответ: M [P] = 2200 кВт, σ
P
= 1307 кВт, P
P
= 5468 кВт.
1.3. Приближенное вычисление числовых характеристик пара-
метров
установивишихся режимов
Т
ЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
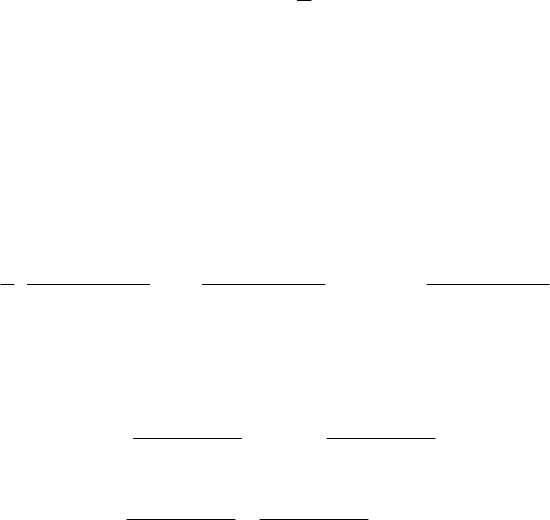
14
Приближенное определение математического ожидания
функции случайной величины Y = ϕ(X) может быть сделано по
формуле
[ ]
( ) ( )
2
1
φ φ σ
2
X X X
M Y m m
′′
≈ +
Дисперсия функции случайной величины Y = ϕ(X) прибли-
женно определяется на основе линеаризованной зависимости по
формуле
[ ]
( )
2
2
φ σ
X X
D Y m
′
≈
.
Для функции двух переменных Z = ϕ(X,Y):
[
]
(
)
( ) ( ) ( )
2 2 2
2 2
2 2
φ ,
φ , φ , φ ,
1
σ cov( , ) σ
2
X Y
X Y X Y X Y
X Y
M Z m m
m m m m m m
x y
x y
x y
≈ +
∂ ∂ ∂
+ + +
∂ ∂
∂ ∂
и
[ ]
2
2
2 2
φ
( , )
φ
( , )
σ σ
φ
( , )
φ
( , )
2 cov( , ).
X Y X Y
X Y
X Y X Y
m m m m
D Z
x y
m m m m
X Y
x y
∂ ∂
= + +
∂ ∂
∂ ∂
+ ⋅
∂ ∂
Упражнения
Упражнение 1
Две электрические системы связаны линией электропередачи
с номинальным напряжением 220 кВ. Длина линии l = 250 км,
удельное реактивное сопротивление x
0
= 0,41 Ом/км. Напряжения
по концам линии поддерживаются постоянными и равными
U
1
= U
2
= 220 кВ. Угол сдвига δ между векторами напряжений U
1
и U
2
является случайной равномерно распределенной величиной
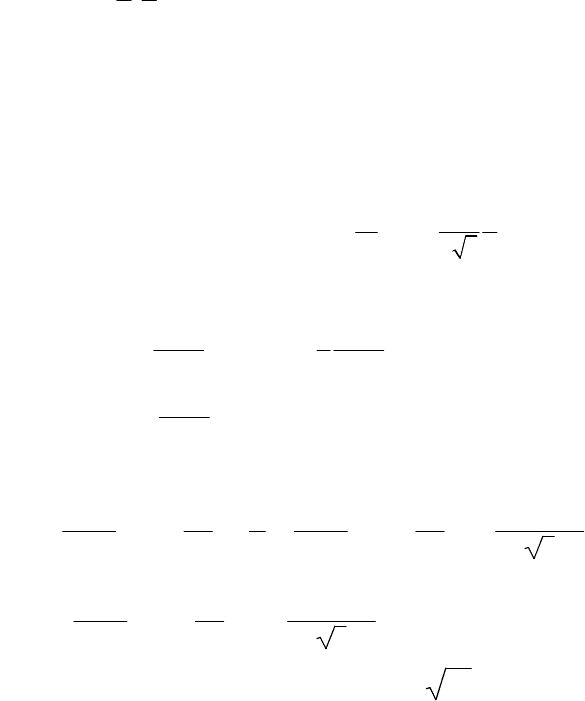
15
в интервале
π π
,
6 3
−
. Пренебрегая активным сопротивлением и
емкостью линии, определить математическое ожидание и средне-
квадратическое отклонение передаваемой мощности.
Вычисления
Сопротивление линии:
X 250 0.41⋅:= X 102.5=
Математическое ожидание и среднеквадратическое отклоне-
ние угла δ соответственно равны
[ ]
δ
π 1 π
δ , σ
12 2
2 3
M = = .
Приближенные формулы для математического ожидания и
дисперсии передаваемой мощности по линии:
[ ] [ ] [ ]
[ ] [ ]
2
1 2 1 2
δ
2
2
1 2
δ
1
sin(
δ ) sin( δ )σ ,
2
cos( δ ) σ .
U U U U
M P M M
X X
U U
D P M
X
≈ −
≈
.
В результате получаем:
M
P
220
2
X
sin
π
12
⋅
1
2
220
2
X
sin
π
12
⋅
⋅
π
2 3⋅ 2⋅
2
⋅−:=
D
P
220
2
X
cos
π
12
⋅
2
π
2 3⋅ 2⋅
2
⋅:=
M
P
109.649= D
P
42774.905= D
P
206.821=
Упражнение 2
В результате расчета получены математические ожидания,
среднеквадратические отклонения и коэффициент корреляции
вещественной и мнимой составляющих напряжения U′ и U′′ на
шинах нагрузки:
M [U′] = 209
кВ, M [U′′] = −24 кВ,
σ
U′
= 9 кВ, σ
U′′
= 3 кВ, r
U′, U′′
= 0,92.
16
Вычислить математическое ожидание и среднеквадратиче-
ское отклонение модуля напряжения.
Вычисления
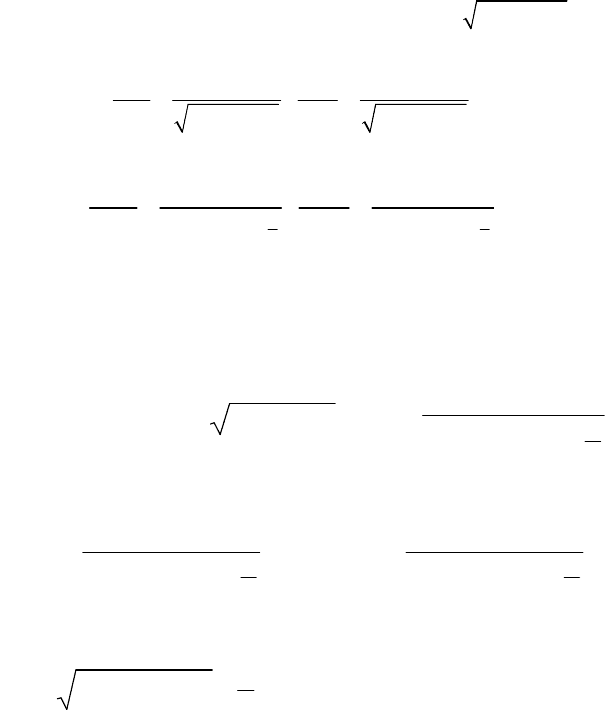
Модуль напряжения вычисляется по формуле
2 2
U U U
′ ′′
= + .
Первые производные от U по U′ и U′′:
2 2 2 2
, .
U U U U
U U
U U U U
′ ′′
∂ ∂
= =
′ ′′
∂ ∂
′ ′′ ′ ′′
+ +
Вторые производные от U по U′ и U′′:
( ) ( )
2 2 2 2
2 3 2 3
2 2 2 2
2 2
,
U U U U
U U
U U U U
′′ ′
∂ ∂
= =
′ ′′
∂ ∂
′ ′′ ′ ′′
+ +
.
Математическое ожидание модуля напряжения:
M
U'
209:= M
U''
24−:= D
U'
9
2
:= D
U''
3
2
:=
cov
U'U''
0.92 D
U'
D
U''
⋅⋅:= A
M
U''
2
M
U'
2
M
U''
2
+
( )
3
2
:=
B
M
U'
M
U''
⋅
M
U'
2
M
U''
2
+
( )
3
2
:= C
M
U'
2
M
U'
2
M
U''
2
+
( )
3
2
:=
M
U
M
U'
2
M
U''
2
+
1
2
A D
U'
⋅ B cov
U'U''
⋅+ C D
U''
⋅+
( )
+:=
M
U
210.39=
Дисперсия модуля напряжения:
17
A
M
U'
M
U'
2
M
U''
2
+
:= B
M
U''
M
U'
2
M
U''
2
+
:=
D
U
A
2
D
U'
⋅ B
2
D
U''
⋅+ 2 A⋅ B⋅ cov
U'U''
⋅+:=
D
U
74.432= D
U
8.627=
Упражнение 3
Вычислить математическое ожидание, дисперсию и средне-
квадратическое отклонение напряжения в конце линии 220 кВ,
если сопротивления линии R и X являются случайными величи-
нами. Зарядной мощностью линии пренебречь.
Сопротивления R и X имеют числовые характеристики:
M[R] = 12,1 Ом, M [X] = 43,5 Ом.
σ
R
= 2,5 Ом, σ
X
= 3,3 Ом.
Нагрузка в конце линии 160 + j
⋅
90 МВ⋅А, напряжение в нача-
ле линии 240 кВ.
Ответ: M [U] = 217 кВ, D [U] = 0,119 кВ
2
, σ
U
= 0,346 кВ.
Упражнение 4
Вычислить математическое ожидание и среднеквадратиче-
ское отклонение потерь мощности в линии с сопротивлением
8 Ом, если случайными величинами являются активная и реак-
тивная мощность, протекающие по линии.
M [P] = 200 MВт, M [Q] = 120 Мвар,
σ
P
= 30 МВт, σ
Q
= 23 Мвар, r
P, Q
= 0,6.
Напряжение принять равным номинальному значению 220 кВ.
Ответ: M [∆P] = 8,99 МВт, D [∆P] = 6,94 МВт
2
, σ
∆P
=
= 2,63 МВт.
Упражнение 5
По линии электропередачи
питаются две нагрузки 1 и 2,
рис. 1.2.
Вычислить математиче-
ское ожидание и среднеквад-
ратическое отклонение сум-
марных потерь мощности в сети, если известно, что мощности
P
1
+jQ
1
P
2
+jQ
2
1
2
Рис.1.2. Схема питания нагрузок
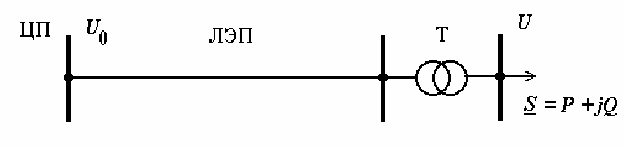
18
обеих нагрузок являются случайными величинами с числовыми
характеристиками:
M[P
1
] = 25 МВт; σ
P1
= 4 МВт;
M[Q
1
] = 20 Мвар; σ
Q1
= 3 Мвар;
M[P
2
] = 50 МВт; σ
P2
= 6 МВт;
M[Q
2
] = 30 Мвар; σ
Q2
= 5 Мвар.
Корреляционная матрица (матрица коэффициентов корреляции)
для этих случайных величин
1 0,9 0,8 0,4
1 0,4 0,8
1 0,9
1
=
r
Номинальное напряжение сети 110 кВ, сопротивления участ-
ков линии R
1
= 6 Ом и R
2
= 5 Ом.Ответ: M [∆P] = 3,87 МВт,
D [∆P] = 0,967 МВт2, σ
∆P
= 0,983 МВт.
З
АДАЧИ
Задача 1. регулирование напряжения в электрической
сети при случайном характере нагрузки
В узле нагрузки оценить уровни напряжения и определить
требования к средствам регулирования напряжения.
Условия и ограничения
Центр питания (ЦП) связан с помощью питающей ЛЭП и по-
нижающим трансформатором с узлом нагрузки (рис.1.3), в кото-
ром имеется большое число мелких потребителей со случайным
характером электропотребления.
Рис.1.3. Схема питания узла нагрузки
Известны установленные мощности всех электроприемни-
ков, однако событие, когда одновременно все электроприем-
19
ники включены и работают с наибольшей мощностью, являет-
ся практически невозможным.
В соответствии с теоремой Ляпунова, сумма бесконечного
числа случайных величин при определенных условиях подчиня-
ется нормальному закону распределения. В практических случаях
с достаточной точностью можно принять, что нормальному зако-
ну подчиняется и сумма большого, но конечного числа случай-
ных величин, в данном случае суммы активных и реактивных
мощностей. Следует также оговорить тот факт, что P и Q потре-
бителей, как правило, коррелируют с большим значением коэф-
фициента корреляции (порядка 0,8...1,0). Таким образом, для лю-
бого момента времени в случайном процессе изменения мощно-
сти нагрузки имеется двухмерный нормальный закон распреде-
ления системы случайных величин P и Q.
Задание
Для режима максимальных нагрузок следует выяснить необ-
ходимость установки дополнительных средств регулирования
напряжения, кроме имеющегося устройства РПН понижающего
трансформатора. При этом следует иметь в виду, что напряжение
на шинах низкого напряжения (НН) понижающего трансформа-
тора в соответствии с принципом встречного регулирования на-
пряжения должно быть в пределах (1,05...1,10) U
ном
.
Современные устройства РПН в основном позволяют регули-
ровать напряжение в пределах ±15 % от U
ном
, т. е. для достиже-
ния нижней границы 1,05 необходимо иметь относительное зна-
чение напряжения на шинах НН не ниже (1,05…0,15) = 0,9.
С учетом случайного характера нагрузок, а следовательно и
напряжений, следует оценить вероятность события, когда напря-
жение оказывается ниже указанного уровня: P(U
*
< 0,9).
В расчетах можно не пользоваться относительными величи-
нами, а вычислять напряжение
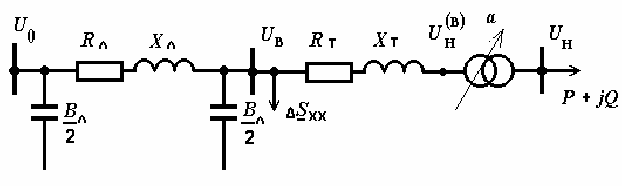
(B)
H
U напряжение технически не-
существующей точки в трансформаторе, но используемой в элек-
трической модели трансформатора (рис. 1.4).
20
Рис.1.4. Схема замещения электрической сети
Сопоставляя область возможных изменений напряжения
(B)
H
U
со значением 0,9U
ном
, можно оценить вероятность появления си-
туации, когда устройством РПН невозможно поднять напряжение
до требуемого уровня. В таких случаях требуется установка до-
полнительных средств регулирования.
Указания к выполнению
1. Для вычисления вероятности попадания напряжения в об-
ласть удовлетворительных значений требуется найти закон рас-
пределения вероятностей напряжения. Поскольку закон распре-
деления узловых мощностей известен, а все другие параметры,
входящие в математическую модель установившегося режима,
являются детерминированными, здесь имеется задача по функ-
циональному преобразованию системы одних случайных величин
(P, Q) в другую, например (U', U'') − вещественная и мнимая со-
ставляющие комплекса напряжения.
2. Одним из методов решения задачи функционального пре-
образования системы случайных величин является метод стати-
стической линеаризации. Используя линеаризованное преобразо-
вание случайных величин, можно при относительно небольших
дисперсиях случайных величин приближенно считать закон рас-
пределения узловых напряжений также нормальным. Для опре-
деления числовых характеристик напряжений в узлах электриче-
ской сети можно воспользоваться следующим способом.
1) Математические ожидания напряжений находятся обыч-
ным способом, как при детерминированном задании данных, на-
пример известным методом "в два этапа" при счете без програм-
мы или по любой программе расчета установившегося режима
электрической сети.
