Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics

Подождите немного. Документ загружается.

4.4 Discrete symmetry 119

4.4 Discrete symmetry

4.4.1 General remarks

One can easily check the invariance of every conserved quantity (e.g., the

above c and A) against the permutations of the elements σ

,aswellasthe

covariance of the systems (4.32) and (4.35). The symmetry with respect to

the cyclic permutation of the variables (or indices) is o bvious if one recalls

its DT o rigin ; hence, this observation is general. For the illustration we again

exploit the simplest KdV case starting from the representation of [438] (for

the additional symmetry with respect to reﬂections see [165]). Let us consider

the periodically closed dressing chain equation of the odd step N =2g +1

and introduce vectorial notations, namely

Σ =(σ

, ..., σ

)

,μ=(μ

, ..., μ

)

and

=(σ

, ..., σ

)

The closed chain equation (4.22) can be rewritten either in the form

(1 + S)Σ

=(1− S)(Σ

+ μ)

or in the form

N−1



k=1

(−1)

(Σ

− μ), (4.36)

where the operator of p ermutation is represented as the matrix S [438]. Both

forms are obviously invariant with respect to the S-transformation because

the matrix S and operators in (4.36) commute. The same statement is valid

for the equations of the time evolution.

Let us emphasize that the right-hand side of (4.36) is tensorial with re-

spect to the components of Σ, so the action of the group transformation is

the tensor (direct) product of the group representations in the corresponding

vector spaces.

If we introduce the cyclic permutation operator T

, its action determines

the matrix S as

= S

= σ

i+1(modN)

The powers of the matrix of the previous section produce the group, S

∈

⊂ S

and give a basis for integration of the covariant equations. The

technique uses the Poisson r epresentation of the system (4.36),

(Σ,μ)={H(Σ,μ),ψ(Σ,μ)},

where the operator

H(Σ, μ)=



i=1



+ μ



120 4 Dressing chain equations

is invariant with respect to the group transformations and deﬁnes a linear

operator ad

with respect to the Poisson bracket

{σ

,σ

} =(−1)

k−i

(1 − δ

),k≤ i.

It is easy to check that

{H(Σ),σ

} =



k=1



{σ

,σ

} + μ

{σ

,σ

}





k=1

(σ

+ μ

){σ

,σ

which yields the system (4.36).

The integration of the system can be understood in a “quantum-mechanical”

language, introducing ﬁrst the “commuting” functions C

(Σ) from the kernel

∈ K:

=0. (4.37)

Next, the eigenvalue problem for ψ(Σ,μ) outside the kernel can be considered

as a matrix one in some basis:

= λ

, (4.38)

where i =1,...,g, N =2g + 1. The symmetry of (4.37) and (4.38) with

respect to the transformations T

(4.18) follows from the obvious relation

H(T

Σ,T

μ)=H(Σ,μ).

This means that matrices of a representation of the symmetry group commute

with the matrix of ad

on the corresponding subspace with constant Casimir

operator.

4.4.2 Irreducible subspaces

The symmetry and the tensor structure of the right-hand side of (4.36) show

that the system may be simpliﬁed in the framework of the Wigner–Eckart

theory [452]. In accordance with the Wigner theorem applied to equations

(4.37) and (4.38), the op erator ad

has the quasidiagonal structure in the

basis of irreducible representations. The projective op erators p

acting on the

irreducible subspaces are deﬁned in the subspaces produced by chains that

appear as the sum over the transformation group action on some basic element.

In the case of the commutative group, chosen for simplicity, the irreducible

matrices are one-dimensional, and the basis is deﬁned by the set of projectors



s∈G

(s)T

where N

are normalizing constants, D

(s) are irreducible representations of

the symmetry group, and T

is the group transformation operator in the space

under considera t ion.

4.4 Discrete symmetry 121

In our case the operator T

coincides with that introduced in the previous

section and in the c ase of the cyclic permutation group C

the irreducible ma-

trices are one-dimensional. Namely, D

(e)=1,D

(s)=a

, D

)=a

,...

with a

=exp(j2πi/N ), where the integer N is the group order.

Hence,

= a

. (4.39)

For N = 3 we project the system (4.36) or, o riginally, (4.26) onto each

subspace, having three equivalent equations. Let a =exp(2πi/3); e.g., the

second of the resulting equations g ives

= n

+ an

+ a

(4.40)

= σ

− σ

+ μ

− μ

+ a



− σ

+ μ

− μ



+ a



− σ

+ μ

− μ



Here n

denotes the right-hand side of (4.26).

The inverse transform from original variables to the basis of irreducible

representations reads

= s

+ s

= s

+ as

+ a

= s

+ a

+ as

Inserting them into (4.40) yields

(x)=0,

(x)=−(a − 1)





+2s



− aμ

+ aμ

− μ

+ μ



and

(x)=(a − 1)





+2s



− aμ

+ aμ

+ μ

− μ



The second conservation law (4.33) in terms of s

allows us to express

the Hamiltonian as a function of the only variable s

. The conservation

laws are obviously the combinations of the i rreducible polynomials σ

.To-

gether with the Hamiltonian (=λ) conservation it leads to the spectral curve

deﬁnition.

Returning to the general problem needs the tensor product space of the

vectors Σ and μ. The problem of solution of (4.37) and (4.38) simpliﬁes if we

use the above symmetry written in terms of



s∈G

(s)T

= N

−1



k=1

k−1

i−1

122 4 Dressing chain equations

Proposition 4.4. By direct application of the operator T

it can be checked

that the tensor pr oducts of s

[see (4.39)]

...s

(4.41)

form a basis of irreducible tensors in the space of polynomials, and the r esult

of the T

operator action diﬀers fr om (4.41) by a constant factor a

...a

The further computations are conveniently made via the Poisson bracket

} = N

−2



i−1

j−1

k−1

l−1

{σ

,σ

}. (4.42)

Particularly it is shown that the C

can be chosen as a combination of

irreducible polynomials (one c an check this statement for the examples in

[438]), and the conservation laws presented are combinations of the irreducible

polynomials of σ

Next, the t-dependence may be introduced via the scheme of Sect. 4.3.

Other nonlinear systems are treated similarly. The widened symmetry, e.g.,

from [165], includes reﬂections at the (Σ,μ) tensor product space and could

give more information about solutions.

4.5 Explicit formulas for solutions of chain equations

(N =3)

Let us return to equations (4.32),

′

= σ

− σ

+ μ

− μ

′

= σ

− σ

+ μ

− μ

′

= σ

− σ

+ μ

− μ

(4.43)

that are equivalent to the system (4.25) under the condition α =0withN =3.

We use two integrals

c = σ

+ σ

A = g

+ μ

(σ

+ σ

)(σ

+ σ

)(σ

+ σ

(σ

+ σ

)+μ

(σ

+ σ

)+μ

(σ

+ σ

(4.44)

From (4.43) we obtain

′

=(σ

− σ

+ μ

− μ

)

Using the ﬁrst equation in (4.44) as σ

= c −σ

−σ

, we obtain the equation

containing σ

′

and σ

. Then we eliminate the remaining variable σ

with the

help of both integrals in (4.44). Thus, we get the equation

′

= σ

− 2(c

+ μ

− 2μ

)σ

− 4(2μc − A)σ

+ c

+2(μ

+ μ

+2μ

− 4Ac +(μ

− μ

)

(4.45)

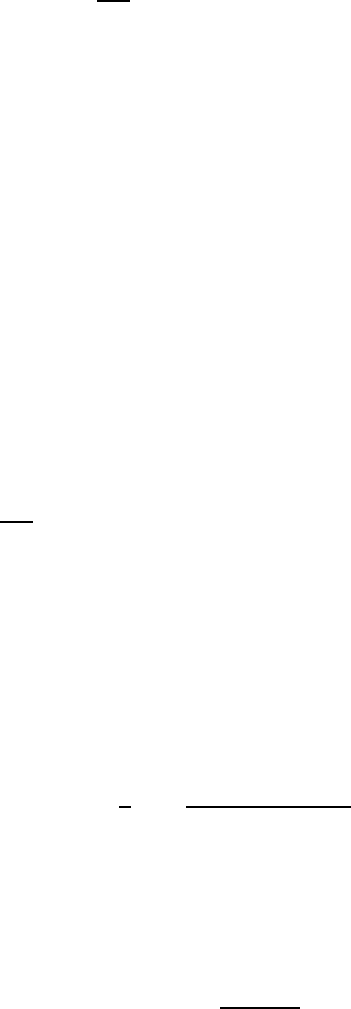
4.5 Explicit formulas for solutions of chain equations (N = 3) 123

This equation has the following structure:



dσ



= σ

− 6aσ

+4bσ

+ d, (4.46)

where a, b,andd are constants determined by (4.45). The extra multipliers

6 and 4 have been included for co nvenience. The relation (4.46) is an elliptic

curve in variables (σ

′

,σ

) and therefore it is uniformized by elliptic func-

tions. Let us build the invariants (capital letters are chosen to distinguish the

invariants from variables g

of the chain)

= d + a

= a

− b

− ad.

So, the pair (b, a)isapointonacurve

=4a

− G

a − G

Therefore, there exists a parameter ν such that the following equations occur:

b = ℘

′

(2ν),a= ℘(2ν),

where ℘ (2ν) is the Weierstrass elliptic function. This means that we take

three new parameters G

, G

,andν insteadoftheoldonesa, b,andd which

in turn depend on ﬁve parameters of the chain: (μ

,μ

,A,c); hence, we

write



dσ



= σ

− 6℘(2ν)σ

+4℘

′

(2ν)σ

+[G

− 3℘(2ν)],

which yields

(x)=ζ(x + ν + x

; G

) − ζ(x − ν + x

; G

) − ζ(2ν; G

Note that σ

is not the Weierstrass σ-function in the theory of elliptic func-

tions, but ζ is the standard Weierstrass ζ-function. The solution σ

(x) depends

on three arbitrary constants [according to the third order of equations (4.43)]

, G

,andx

which are in turn deﬁned by ﬁve constants μ

, A,andc in

explicit but transcendental way. Parameter ν is not exceptional,

ν =

℘

−1



+ μ

− 2μ

+ c



where ℘

−1

denotes the ellip tic integral of the ﬁrst kind (inversion of the elliptic

function ℘).

Remark 4.5. The solution obtained is exactly the logarithmic derivative of the

Ψ-function for the one-gap Lam´e potential,

′′

− 2℘(x)Ψ = λΨ, Ψ =

σ(α − x)

σ(α)σ(x)

ζ(α)x

,λ= ℘(α),

124 4 Dressing chain equations

and is distinguished from the solution

′

= ζ(α − x) − ζ(α) − ζ(x)

by a shift of the spectral parameter α.

Remark 4.6. If one is interested in σ

(4.46) in connection with the KdV equa-

tion theory, the dependence on time can be obtained using the t-chains [274]

obtained by means of the MKdV equation for σ and conservation laws [443]

(see the previous sections).

4.6 Towards the spectral curve

It is known that there exists a cla ss of periodic or quasip eriodic potentials

of the op erator (4.18) for which the sp ectral problem in L

leads to the con-

tinuous spectrum with the ﬁnite number of gaps, i.e., intervals at which the

values of the parameter λ do not belong to the spectrum [45]. Potentials of

this kind exempliﬁed in Sect. 4.5 correspond to solutions of the KdV equa-

tion, if time dependence is introduced by means of the Lax pair [215, 353].

The important explicit formulas for eigenfunctions of the operator (4.18) were

obtained in [215]. As mentioned already, the chain equations closed (period-

ically) on an odd step 2g + 1 produce the ﬁnite-gap solutions [438, 448]. We

have demonstrated already that for g = 1 the potentials are expressed in the

elliptic Weierstrass or Jacobi functions.

Further development allows us to include an additional evolution variable

y [45, 55].

As shown in Sect. 4.2, especially the comments on Proposition 4.1, the

value of the parameter α depends on the interpretation of σ.Thecaseα =0

corresponds to σ = φ

−1

,whereφ is the eigenfunction of the operator (4.18)

with the eigenvalue μ;itdiﬀersfromthatforα = 0. For general statements

and some applications see [284].

Let us consider the periodically closed (σ

n+N

= σ

,α

n+N

= α

)chain

(4.25). Below we follow [17, 438] for the formalism of the 2 × 2Laxpair

(denoted as U and V ) and [422, 423] for the link to the spectral curve and the

Dubrovin equations concentrating mostly on the case of ﬁnite-gap solutions

for N =2g +1.

As follows from (4.19), the link of the variable σ to the potential u

con-

nects the corresponding matrix operators. Let us start from the spectral equa-

tion

−ψ

′′

+ u

= λψ

. (4.47)

With the ﬁrst-order dressing chain equation in mind, it is useful to rewrite

(4.47) in the matrix form. Speaking in physical language, we introduce the

column of “state”



′



4.6 To wards the spectral curve 125

which is a solution of

′

= U

(μ)Φ

. (4.48)

is easily found from (4.47). Diﬀerentiation of the DT (4.23) gives

′

n+1

(λ + α

)=(u

− λ)ψ

(λ) − σ

′

(λ) − σ

′

(λ), (4.49)

or, using (4.19) with the choice c

=0,gives

′

n+1

(λ + α

)=(σ

− λ)ψ

(λ) − σ

′

(λ).

In terms of the column Φ

the result may be written as

n+1

(λ + α

)=V

(λ)Φ

. (4.50)

The ﬁrst row of this vector relation is simply (4.23) and the second line follows

from (4.49) after use of the Miura link (4.19). Both (4.48) and (4.50) form the

Adler Lax pair [17]

(λ)=



−σ

− λ −σ



(λ)=



− λ 0



. (4.51)

The operators satisfy the diﬀerential equation (Lax compatibility condition)

with a shifted spectral parameter that is equivalent to the chain equation

′

= U

(λ + α

(λ) − V

(λ)U

(λ). (4.52)

Now we can reformulate the chain closure condition in terms of the operators

. The operator V

(λ) maps the state Φ

onto the space Φ

(λ + α

), the

operator V

(λ + α

)mapsΦ

onto Φ

(λ + α

+ α

) and so on, till

N+1

(λ + α)=(−1)

T (λ)Φ

(λ),

where the transition operator

T (λ)=



n=1

(λ + β

n−1

) (4.53)

is introduced, whence



i=1

,β

=0,β

= α.

Equation (4.52) yields the x-evolution equation for T (λ):

′

(λ)=U

(λ + α)T (λ) − T (λ)U

(λ).

Let the eigenvalue of the operator T (λ) be denoted as z, then the condition

det[zI − T (λ)] = z

− P (λ)z + Q(λ) = 0 (4.54)

126 4 Dressing chain equations

introduces the hyperelliptic spectral curve in the complex (λ, z)-plane. The

spectral invariant

Q(λ)=detT (λ)=(−1)

N−1



n=0

(λ + β

) (4.55)

is evaluated via (4.53). Note that det V (λ+β

)=λ+β

. The coeﬃcient P (λ)

is given by

P (λ)=trT (λ)=A(λ)+D(λ),

for

T (λ)=





, (4.56)

where, for the case of N =2g +1,

A =(−1)

g+1

cλ

+ a

g−1

+ ..., B = b

+ b

g−1

+ ...,

C =(−1)

g+1

+ c

+ ..., D=(−1)

g+1

cλ

+ d

g−1

+ ...,

=(−1)

, c =



k=1

(−1)

, which may be proved by induction using the

deﬁnitions (4.53) and (4.51) of the matrices T and V . One starts with g =1,



−σ

− λ −σ



−σ

− λ − β

−σ



−σ

− λ − β

−σ



and applies the induction. This results in

P (λ)=



n=0

g−n

. (4.57)

Substitution of (4.56) into (4.52) yields

′

= C − (λ + u

)B, (4.58)

′

= D − A, (4.59)

′

=(λ + α + u

)A − (λ + u

)D, (4.60)

′

=(λ + α + u

)B − C. (4.61)

Using (4.58) and (4.61), one can check that

′

(α)=αB(λ);

hence, when α = 0, the coeﬃcients I

of the p olynomial P (λ)areconstants

of motion. We can compare the results that follow from (4.42) and the con-

servation laws from Sect. 4.3 and (4.44).

The transformation of the sp ectral curve (4.54) to the normal form [208]

is performed by the substitution

z =

P (λ)+y

which yields

= P (λ)

− 4Q(λ). (4.62)

4.7 Dubrovin equations. General ﬁnite-gap p otentials 127

4.7 Dubrovin equations. General ﬁnite-gap potentials

Let us introduce a system of moving points o n the hyperelliptic spectral curve

(4.54) and (4.62). Namely, note that at the points λ = λ

such that

B(λ)=



j=1

(λ

− λ), (4.63)

the transition matrix T is triangular

T (λ



A(λ

C(λ

) D(λ

)



. (4.64)

This allows us to choose the eigenvalue

= A(λ

which means the g-tuple of points (λ

)ofthe(λ, z)-plane belongs to the

spectral curve

− P (λ

+ Q(λ

)=0. (4.65)

The Abel–Jacobi mapping AJ: Γ

(g)

→ Jac(Γ) sends the degree g divisor

Di = (λ

)+... +(λ

)

of Γ , i. e., an element of the g-fold symmetric product Γ

(g)

of Γ ,toapoint

of the Jacobi variety Jac(Γ).

Let us show that the x-motion of the g-tuple of points follows from (4.56),

which means that a dependence of λ

on x is linearized on Jac(Γ ). The motion

is extracted from the derivative of B(λ

) = 0 [see (4.63)],

′

(λ

)+B

(λ

)λ

′

=0.

Taking (4.59) for B

′

= A(λ

) − D(λ



P (λ

)

− 4Q(λ

) and using the

identity

P (λ

)

− 4Q(λ

)

=[A

+2AD + D

− 4AD]

λ=λ

yields from (4.64) and (4.57) the generalized Dubrovin equations

′



P (λ

)

− 4Q(λ

)

(λ

)

. (4.66)

Here the numerator is expr essed as the diﬀerence of the roots of quadratic

equation (4.65) (eigenvalues of the matrix T ). The equations (4.66) appeared

(perhaps for the ﬁrst time) in the paper of Drach [130]. The comprehensive de-

scription of the ﬁnite-gap potentials in the context of algebrogeometric theory

is given in [45]; see also [78] with the historical remarks on the theory.

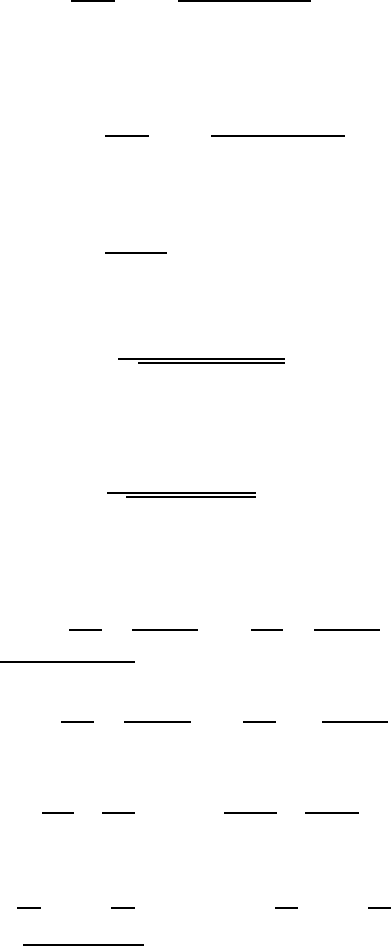
128 4 Dressing chain equations

The Lagrange interp olation formula reads

F (λ)

B(λ)



j=1

F (λ

)

(λ

)(λ − λ

)

+ G(λ), (4.67)

where F (λ)andG(λ) are polynomials. In particular, if F (λ)=λ

,k =

0, ..., g − 1, the application of (4.67) gives

B(λ)



j=1

(λ

)(λ − λ

)

Let us take (4.63) for distinct λ

s and pick out the residue of both sides at

λ = ∞:



j=1

(λ

)

= δ

k,g−1

,k=1,...,g. (4.68)

Substitution of the formula for B

(λ

) yields



j=1

′



P (λ

)

− 4Q(λ

)

= δ

k,g−1

Integration of the equations is realized on a complex torus C

/L that repre-

sents the Jacobi variety of the image AJ(Di) of the divisor Di:



j=1



dλ



P (λ)

− 4Q(λ)

= δ

k,g−1

x +const. (4.69)

Let us trace the technical details of integration of the dressing chain equations,

starting from the Drach–Dubrovin equations (4.66) for g =2.Namely,the

system

dλ

− λ

dλ

− λ

with ν



P (λ

) − 4Q(λ

)isequivalentto

dλ

− λ

dλ

= −

− λ

which yields (4.68)

dλ

=0,

dλ

=dx.

Integration leads to quadratures:



dλ



dλ

= a



dλ



dλ

= x + a

where ν = ±



P (λ) − 4Q(λ); see again (4.55) and (4.57).

In the case α = 0 the algebrogeometric method [45] a pplies the Lagrange

interp olation formula to the system (4.66).