Добржанська О.Л. Системний аналіз

Подождите немного. Документ загружается.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

Припустимо, що X вимірюється в ранговій шкалі, Y - в інтервальній

шкалі (або відносній). Для таких величин можна перетворити оцінки Y в

ранги і знайти коефіцієнти рангової кореляції Спірмена або Кендала.

Обидві змінні вимірюються за ранговою (порядковою) шкалою:

Для таких величин вихідні дані можуть бути перетворені в ранги або

просто бути рангами, при цьому обчислюються коефіцієнти рангової

кореляції. Таких коефіцієнтів декілька, один з яких коефіцієнт рангової

кореляції Спірмена -R

()

−

∑

−=

де

змінні X і Y набувають значення 1,2,…,n ;

n - кількість рангів;

-y

)- різниця між рангом i-го об'єкта по X і його ж рангом по Y.

Коефіцієнти рангової кореляції вимірюють тісноту зв'язку між

величинами, які можна розставити за зростанням чи зниженням ступеня

інтенсивності кожної. Така процедура має назву ранжування ряду.

Ряд величин можна ранжувати за двома і більше властивостями і

якщо існує тенденція одночасного збільшення (зменшення) двох

властивостей, то це означає, що між цими властивостями існує зв'язок.

При наявності n послідовних і необ'єднаних рангів 1,2,…,n,

використовується коефіцієнт рангової кореляції Кендала:

де S = P-Q,

/)(

−=

nnC

Р - кількість пар рангів з прямим порядком;

Q - кількість пар рангів з зворотним порядком;

n - загальна кількість рангів.

При τ=+1 всі пари рангів мають прямий порядок; при τ=-1 всі пари

мають зворотний порядок рангів; при τ=0 кількість пар з прямим і

зворотним порядками рангів однакова.

Також для обчислення коефіцієнта рангової кореляції τ можна

використовувати способи, що не потребують складання таблиці, кількості

пар рангів. Для цього формула τ перетворюється так, щоб вона містила або

кількість пар рангів з прямим порядком Р, або зі зворотним порядком Q:

/)(/)(/)( −

•

−=−

−

•

−

Коефіцієнт рангової кореляції Спірмена перевищує коефіцієнт

рангової кореляції Кендела, хоча значення двох коефіцієнтів достатньо

великі, що свідчить про істотний зв'язок між величинами Х та У.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

Відмінність між цими коефіцієнтами полягає в тому, що при

визначенні коефіцієнта рангової кореляції Кендела τ фіксується тільки

факт прямого або зворотного розташування рангів для кожної пари

елементів, незалежно від віддалення рангів один від одного.

Одна із змінних вимірюється за номінальною, а інша - за

кількісною шкалою:

Для таких величин визначення зв'язку між X і Y зручно

використовувати наступну формулу:

()

0101

−

nnxx

, де

- середнє відхилення по X об'єктів, що мають одиниці по Y;

- середнє відхилення по X об'єктів, що мають нулі по Y;

- стандартне відхилення n значень по X;

- число об'єктів, що мають одиницю по Y;

- число об'єктів, що мають нуль по Y.

Обидві змінні вимірюються за номінальною шкалою:

Для таких величин коефіцієнт кореляції можна обчислити за

формулою:

yyxx

yxxy

qpqp

ppp

−

, де

- частка об'єктів, що мають одиницю по X ;

- частка об'єктів, що мають нуль по X;

- частка об'єктів, що мають одиницю по Y;

- частка об'єктів, що мають нуль по Y;

- частка об'єктів, що мають одиницю по X і по Y одночасно.

ИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. Охарактеризувати типи шкал, що використовуються для вимірювання

випадкових величин в системі.

2. Охарактеризувати основні етапи кореляційного аналізу.

3. Охарактеризувати коефіцієнт кореляції, та його показники.

4. Охарактеризувати поняття множинної кореляції.

5. Охарактеризувати поняття приватної кореляції.

6. Визначити коефіцієнт кореляції, що використовується, для номінальних

величин.

7. Визначити коефіцієнт кореляції, що використовується якщо одна із

змінних вимірюється за номінальною, а інша - за кількісною шкалою.

8. Визначити для яких величин застосовується коефіцієнт кореляції

Спірмена.

9. Визначити для яких величин застосовується коефіцієнт кореляції

Кендела.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

10.

Визначити для яких величин застосовується коефіцієнт кореляції

Пірсона.

Джерела інформації : [1, 4, 7, 8, 10, 11, 15, 17, 18]

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

ТЕМА №7. РЕГРЕСІЙНИЙ ТА ФАКТОРНИЙ АНАЛІЗ

7.1. М

ЕТОД РЕГРЕСІЙНОГО АНАЛІЗУ

. Л

ІНІЙНА РЕГРЕСІЯ

.................. 44

7.2. З

АГАЛЬНА ХАРАКТЕРИСТИКА ФАКТОРНОГО АНАЛІЗУ

................... 46

7.3. Ц

ЕНТРОІДНИЙ МЕТОД

Л. Т

ЕРСТОУНА

.......................................... 47

ИТАННЯ ДЛЯ САМОКОНТРОЛЮ

.......................................................... 49

7.1. М

ЕТОД РЕГРЕСІЙНОГО АНАЛІЗУ

. Л

ІНІЙНА РЕГРЕСІЯ

При вивченні імовірнісних залежностей використовується один із

найбільш поширених методів опрацювання даних - метод регресійного

аналізу. Він складається з визначення загального вигляду рівняння

регресії, побудові статистичних оцінок невідомих параметрів, що входять

у рівняння регресії, і перевірці статистичних гіпотез про регресію.

Відмінною особливістю рівнянь, які використовуються у цьому

випадку, є наявність двох видів змінних - залежних і незалежних. На

практиці часто використовують моделі, у яких є одна залежна змінна -

функція і декілька незалежних змінних аргументів:

Y=F(X

,...X

)

Поділ змінних на залежну і незалежні в регресійному аналізі завжди

проводиться на основі змістовних понять.

У найпростішому випадку є одна залежна й одна незалежна змінна,

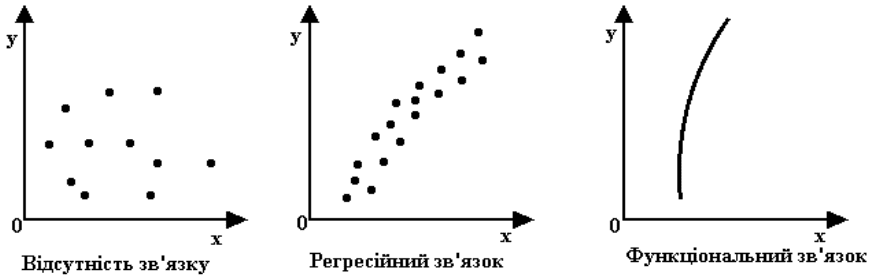
множинна регресія має декілька незалежних змінних (регресорів). Загальна

обчислювальна задача, яку вирішують при аналізі методом множинної

регресії, складається в наближені прямої лінії до деякого набору крапок.

Лінія регресії будується так, щоб мінімізувати квадрати відхилень

цієї лінії від крапок, тому цю процедуру іноді називають оцінюванням по

методу найменших квадратів.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

Пряма лінія на площині (у просторі двох вимірів) задається

рівнянням:

Y=a•X +b.

де змінна Y може бути виражена через кутовий коефіцієнт a

помножений на змінну X плюс константа b. Кутовий коефіцієнт a

називають регресійним коефіцієнтом, а константу b - вільним членом.

Висувається наступна гіпотеза: випадкова величина Y при

фіксованому значенні величини X розподілена нормально з

математичним очікуванням

= a• X + b і дисперсією D

, що не залежить від X.

При наявності результатів спостережень над парами X

і Y

попередньо обчислюються середні значення M

і M

, а потім

вираховується оцінка регресійного коефіцієнта a:

•=

, де

- коефіцієнт кореляції

Sy, Sx - середньоквадратичні відхилення по X та Y, відповідно.

За отриманим регресійним коефіцієнтом a вираховується оцінка

вільного члена b:

b = M

- a

•

та проводиться перевірка значимості отриманих результатів.

Регресійний коефіцієнт a та вільний член b можна знайти і не

обраховуючи математичне очікування, середньоквадратичне відхилення та

коефіцієнт кореляції. Для цього застосовуються формули:

;

∑∑

∑∑∑

===













−

xxn

YXYXn

111

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

∑∑

∑∑ ∑∑

== ==













−

iiiii

xxn

yxxyx

11 11

Основне концептуальне обмеження всіх методів регресійного аналізу

полягає в тому, що вони дозволяють знайти тільки числові залежності, а не

причинні зв'язки.

7.2. З

АГАЛЬНА ХАРАКТЕРИСТИКА ФАКТОРНОГО АНАЛІЗУ

Функціонування будь-якої відкритої системи відбувається в умовах

складної взаємодії комплексу внутрішніх і зовнішніх факторів.

Методи факторного аналізу дозволяють встановлювати причинно-

наслідкові зв'язки, давати їм кількісну характеристику і вимірювати вплив

факторів на функціонування системи.

Досліджувані в системному аналізі фактори можуть бути

класифіковані по різних ознаках:

−

по природі походження;

− по ступені впливу на систему (основні і другорядні);

− по відношенню до навколишнього середовища (внутрішні і зовнішні);

− по ступені поширеності (загальні і специфічні);

− за часом впливу на систему (постійні і перемінні);

− по характеру дії (інтенсивні і екстенсивні);

− за структурою (прості і складні);

− за рівнем ієрархії.

Крім цього фактори підрозділяються на об'єктивні, що не залежать

від волі і бажань людей, та суб'єктивні, що піддаються впливу діяльності

юридичних і фізичних осіб.

Кількісна характеристика взаємозалежних явищ здійснюється за

допомогою показників. Показники, що характеризують причину,

називаються факторними (незалежними); показники, що характеризують

наслідок, називаються результативними (залежними).

Для систематизації факторів створюються спеціальні факторні

системи.

Факторна система - сукупність факторних і результативних ознак,

зв'язаних причинно-наслідковим зв'язком.

Модель факторної системи - це математична формула, що виражає

реальні зв'язки між аналізованими явищами. У загальному виді вона може

бути представлена як:

У=F(X

, X

,...,X

), де У - результативна ознака; Х

- факторні ознаки.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

В основі факторного аналізу лежить виявлення, оцінка і

прогнозування впливу факторів на зміну результативного показника.

У загальному випадку можна виділити наступні основні етапи

факторного аналізу:

1. Постановка мети аналізу.

2. Добір факторів, що визначають досліджувані результативні

показники.

3. Класифікація і систематизація факторів з метою забезпечення

комплексного і системного підходу до дослідження їхнього впливу на

систему.

4. Визначення форми залежності між факторами і результативним

показником.

5. Моделювання взаємозв'язків між результативним і факторним

показниками.

6. Розрахунок впливу факторів і оцінка ролі кожного з них у зміні

величини результативного показника.

7. Робота з факторною моделлю (практичне її використання для

керування процесами в системі).

Набір методів факторного аналізу в даний час достатнє великий та

нараховує десятки різних підходів і прийомів обробки даних. До методів

факторного аналізу відносять:

− центроідний метод Л. Терстоуна;

− однофакторну модель Ч. Спірмена;

−

біфакторну модель Г. Хользінгера;

− груповий метод Л. Гуттмана і П. Хорста;

− метод головних факторів Г. Томсона;

− метод максимальної правдоподібності Д. Лоулі;

− мінімальних залишків Г. Хармана;

− канонічного факторного аналізу К. Рао;

− та ін.

За допомогою факторного аналізу в конкретному дослідженні

вирішуються наступні задачі:

Зменшення розмірності даних.

Визначення кількості факторів.

Визначення факторного навантаження.

Навантаження - це фактично регресійний коефіцієнт, що показує, яку

вагу має даний фактор для прогнозування значення відповідної змінної.

Інтерпретація факторів.

7.3. Ц

ЕНТРОІДНИЙ МЕТОД

Л. Т

ЕРСТОУНА

Метод дозволяє виділяти декілька латентних і характерних факторів

і дає можливість співвідносити факторне рішення з вихідними даними.

Основне співвідношення факторного аналізу:

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

ijii

ezbX

+•=

∑

, j=1,2,3,...,n де

- факторні навантаження;

- залишковий фактор, незалежний від k загальних факторів;

- коефіцієнт факторного навантаження j-го фактора на i-ту змінну.

Загальна постановка задачі складається з:

− побудови та аналізу кореляційної матриці;

−

визначення числа факторів;

− визначення факторного навантаження;

− інтерпретація факторів;

−

визначення змістовного значення факторів.

Відповідно до постановки задачі факторному аналізу завжди передує

кореляційний аналіз. В загальному випадку кореляційна матриця має

вигляд:

XnXmXnXXnX

XmXXXXX

rrr

...

............

...

22212

12111

де елементи головної діагоналі (r

X1X1

, r

X2X2

, ..., r

XnXm

) дорівнюють 1.

На основі цієї матриці будується редукційна матриця зі спільностями

на головній діагоналі. Існують різні методи будування спільності,

найпростіший з який є метод найбільшого елемента по рядку. Суть

методу полягає в тому, що в рядку матриці R вибирається елемент із

найбільшим абсолютним значенням і це найбільше значення записується

на головній діагоналі:

rXnXXnX

XmXrXX

XmXXXr

MAXrr

rMAXr

rrMAX

...

............

...

212

121

Елементи, що знаходяться на перетинанні рядків і стовпців,

називаються навантаженнями (loadings) змінних на фактори.

Далі визначається кількість факторів, обчислюються коефіцієнти

факторного навантаження і надається змістовна інтерпретація факторам.

Для отримання навантаження першого фактора необхідно знайти

суми стовпців редукційної матриці, та суму кожного стовпця розділити на

квадратний корінь із суми всіх елементів цієї матриці:

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

∑

, де Т - сума всіх елементів матриці.

Для отримання навантаження другого фактора необхідно знайти

залишкову матрицю, для цього з кожного елемента матриці віднімається

добуток відповідних навантажень:

для елементів головної діагоналі -

jiiij

brr

ост

−=

для інших елементів -

iiij

bbrr

ост

•−=

Далі необхідно знайти суми стовпців залишкової матриці (всі

значення елементів матриці беруться по модулю), та суму кожного стовпця

розділити на квадратний корінь із суми всіх елементів цієї матриці.

Якщо факторів більше ніж два, процедура повторюється знов.

Для відповідної інтерпретації даних треба відновити змінені знаки.

Для одержання значень факторних дисперсій застосовується

формула:

jiiii

hhhh ...

, де

- факторне навантаження на 1 фактор і змінної;

- факторне навантаження на 2 фактор і змінної;

- факторне навантаження на j фактор і змінної.

При сумуванні квадратів факторного навантаження на фактор по всіх

ознаках визначається оцінка внеску кожного фактора в сумарну дисперсію

параметрів.

ИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. Визначити основні етапи регресійного аналізу.

2. Охарактеризувати поняття залежної та незалежної змінної.

3. Визначити методи прогнозування залежної змінної по незалежним

змінним.

4. Охарактеризувати основні цілі застосування регресійного аналізу.

5. Визначити роль коефіцієнта кореляції в регресійному аналізі.

6. Охарактеризувати регресійний коефіцієнт та вільний член регресійного

рівняння.

7. Класифікувати фактори за різними ознаками.

8. Визначити поняття - факторна система

9. Проаналізувати основні етапи факторного аналізу:

10. Проаналізувати алгоритм роботи центроідного методу в факторном

аналізі.

Джерела інформації : [1, 4, 6, 7, 8, 10, 11, 15, 17, 18]

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.

ТЕМА №8. АВТОМАТИЗОВАНИЙ АНАЛІЗ МІЖНАРОДНИХ

ПОДІЙ

8.1. К

ОМП

ЮТЕРНІ СИСТЕМИ АНАЛІЗУ ДАНИХ

. П

АКЕТИ ПРИКЛАДНИХ

ПРОГРАМ СТАТИСТИЧНОГО АНАЛІЗУ

. КЛАСИФІКАЦІЯ СТАТИСТИЧНИХ

ПАКЕТІВ ПРИКЛАДНИХ ПРОГРАМ

.................................................................... 50

8.2. З

АГАЛЬНА ОРГАНІЗАЦІЯ ІНСТРУМЕНТАРІЮ ПАКЕТІВ ПРИКЛАДНИХ

ПРОГРАМ

.......................................................................................................... 52

8.3. ВИКОРИСТАННЯ ЕЛЕКТРОННИХ ТАБЛИЦЬ В СИСТЕМНОМУ АНАЛІЗІ

МІЖНАРОДНИХ ВІДНОСИН

.............................................................................. 53

ИТАННЯ ДЛЯ САМОКОНТРОЛЮ

.......................................................... 56

8.1. К

ОМП

ЮТЕРНІ СИСТЕМИ АНАЛІЗУ ДАНИХ

. П

АКЕТИ ПРИКЛАДНИХ

ПРОГРАМ СТАТИСТИЧНОГО АНАЛІЗУ

. К

ЛАСИФІКАЦІЯ СТАТИСТИЧНИХ

ПАКЕТІВ ПРИКЛАДНИХ ПРОГРАМ

Комп'ютерні системи для аналізу даних - це наукомісткі програмні

продукти, які широко застосовуються у дослідницькій і практичній роботі

в найрізноманітніших областях сучасного суспільства.

Сучасний світовий і вітчизняний ринок характеризується

різномастістю комп’ютерних систем та статистичних програмних

продуктів (СПП), по офіційним даним Міжнародного статистичного

інституту, число найменувань СПП наближається до тисячі (Statistica;

SAS; Statgraphics+; Minitab; Systat; S-Plus; Клас-Майстер, Stadia;

PolyAnalyst, ...).

Пакети програм статистичного аналізу можна поділяти на чотири

групи:

інтегровані метода-орієнтовані пакети загального призначення;

спеціалізовані метода-орієнтовані пакети;

q предметно - (чи проблемна -) орієнтовані пакети;

навчальні програми.

Якість СПП визначає:

вхідна мова пакета;

статистична різноманітність;

керування даними;

графіка;

швидкість обчислень;

якість вихідних форм;

легкість використання;

легкість навчання;