Добржанська О.Л. Системний аналіз
Подождите немного. Документ загружается.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
21
та потрібного обладнання, чи небажання описувати процес повністю.
Таким чином, випадковість – міра недоступності знань для дослідника.
За типом випадкові величини поділяються на неперервні та
дискретні.
Неперервні величини набувають будь які значення на заданому
інтервалі.
Дискретні величини набувають конкретні, заздалегідь обумовлені
значення.
Для випадкових величин використовують спеціальні статистичні
методи їхнього опису та аналізу, що базуються на законах теорії
ймовірностей.
3.2. К
ЛАСИФІКАЦІЯ ПОДІЙ
. М
ЕТОДИ АНАЛІЗУ ЙМОВІРНОСТЕЙ
ВИПАДКОВИХ ПОДІЙ
Подія - будь який факт, який за результатом досліду може
відбутися, чи не відбутися.
Елементарна подія – подія яку неможливо розкласти на менші події
(множини).
Складна подія – подія яку можна розкласти на множину
елементарних подій.
Події за результатом поділяються на:
−
достовірні (відбудуться обов’язково);
−
неможливі (не відбудуться ніколи);
−
випадкові (можуть відбутися, чи не відбутися).
Імовірність – числова характеристика, що відображає можливість
появи події за результатом експерименту, який повторюватися необмежену
кількість разів.
Про імовірність події можна казати тільки в рамках певного
дослідження.
Числове значення імовірності достовірної події дорівнює 1,
неможливої дорівнює 0, випадкової знаходиться в інтервалі від 0 до1
(включаючи 0 та 1).
Якщо в конкретному експерименті поява події A виключає появу
події В, такі події називають несумісними.
Якщо в конкретному експерименті поява події A не виключає появу
події В, такі події називають сумісними.
Якщо в конкретному експерименті поява події
A, складається з того
що подія A не відбувається, такі події називають протилежними та їх
імовірність пов’язана співвідношенням:
Р(
A) = 1 - Р(A)
Якщо в конкретному експерименті поява події A не залежить від
появи події В, такі події називають незалежними, в протилежному
випадку - залежними.
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
22
Поняття залежність та сумісність подій характеризують різні
властивості подій і їх не можна плутати. Несумісні події завжди залежні
(згідно визначення несумісних подій, поява подія A повністю виключає
появу події В). Сумісні події можуть бути як залежними, тек і незалежними
(згідно визначення сумісних подій, якщо подія A відбулась то відбудеться
чи не відбудеться подія В залежить від умов експерименту).
Якщо імовірність того, що подія А відбудеться дорівнює P(А), то
імовірність того, що подія не відбудеться, дорівнює: Р(
A) = 1 - Р(A)
Імовірність одночасного настання двох незалежних подій
визначається добутком їхніх ймовірностей:
P(АВ) = P(А)
•
P(В).
Якщо результатом експерименту можуть бути несумісні у сукупності
події А1, А2, ...Аn (за умовою, що тільки ці події можуть бути
результатом), то їх множина утворює повну групу подій (вичерпну
множину), для якої справедливє рівняння:
1=
∑
i
i
A )P(
Якщо кожного разу, як відбувається подія А, відбувається подія В, то
говорять, що подія В є наслідком події А, чи що з події А витікає подія В
(позначається: А
⊂
В чи В
⊃
А ). Для таких подій справедлива нерівність:
Р(А)
≤
Р(В)
Умовна імовірність – імовірність здійснення події A при умові, що
відбулась подія В (позначається як Р(A|В)).
Якщо події А та В незалежні, тоді Р(A|В)= Р(A).
Імовірність одночасного настання двох залежних подій
визначається формулою Байеса
P(А|B)
•
P(B) = P(B|А)
•
P(А)
де ліворуч і праворуч записане те саме — імовірності одночасного
настання двох залежних подій.
Якщо доповнити цю формулу загальним виразом безумовної
імовірності події А, отримаємо формулу
P(А) = P(А|B)
•
P(B) + P(А|B)
•
P(B),
що означає: дана подія А може відбутися або після того як подія B
відбулася, або після того, як воно не відбулася (B) — третього варіанту не
істує.
Формули Байеса чи байесовский підхід до оцінки імовірнісних
зв'язків для простих подій і дискретно розподілених випадкових величин
відіграють вирішальну роль при прийняті рішення в умовах
невизначеності. У цих умовах ключовою є стратегія керування, що
базується на прогнозі апостеріорної імовірності події.
Якщо подія В є наслідком події А, та утворює множину n подій:
{B
1
,B
2
,...,B
n
}, то імовірність події А розраховується за формулою:

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
23
∑
=
=
n
i
ii
BAPBPAP
1
)|()()(
яку називають формулою повної імовірності.
В цій схемі подія А відбувається тільки разом з якоюсь В
i
подією із
множини {B
1
,B
2
,...,B
n
}. Така В
i
подія виступає як єдиноможлива подія з
множини {B
1
,B
2
,...,B
n
}, та взаємовиключаюча умова, що визначає появу
події А, чи як гіпотеза, при підтверджені якої відбудеться подія А.
Ця формула прогнозує можливість появи події А за відомими
апріорними ймовірностями здійснення гіпотези.
Апріорні та апостеріорні імовірності пов’язані співвідношенням, яке
має назву теорема гіпотез чи формула Байеса:
)(
)|()(
)|()(
)|()(
)|(
AP
BAPBP
BAPBP
BAPBP
ABP
ii
n
i
ii
ii
i
•
=
•
=
∑
=
1
.
яка оцінює здійснення кожної гіпотези, якщо подія А відбулась.
Якщо між подіями А і В немає зв’язку (одна не залежить від іншої),
то дана формула перетворюється в тривіальну тотожність, ця обставина
використовується при вирішенні задач оцінки тісноти зв'язків в
кореляційному аналізі.
3.3. Р
ОЗРАХУНОК ЙМОВІРНОСТЕЙ ПОДІЙ
,
ЯК СПІВВІДНОШЕННЯ
КІЛЬКОСТІ СПРИЯТЛИВИХ РЕЗУЛЬТАТІВ ДО ЗАГАЛЬНОГО ЧИСЛА
РЕЗУЛЬТАТІВ
Припустимо, що підсумком деякого дослідження може бути кінцеве
число n несумісних та рівноможливих результатів і, що в m сприятливих
результатах відбувається подія А. Тоді імовірність події А дорівнює
співвідношенню числа сприятливих результатів m до загального числа
результатів n:
n
m
WAP
==
)(
, де W - відносна частота.
Якщо порушується хоча б одна з трьох умов (кінцєвість,
несумісність, рівновірогідність), ця формула не працює.
При використанні цього методу необхідно врахувати всі можливі
сприятливі результати. Характерною помилкою для цього методу є
поєднання різних (хоча і дуже схожих) сприятливих результатів в один.
Кількість всіх можливих сприятливих результатів легше
підрахувати, якщо оформити результати дослідження у вигляді таблиці чи
графа.
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
24
3.4. Р
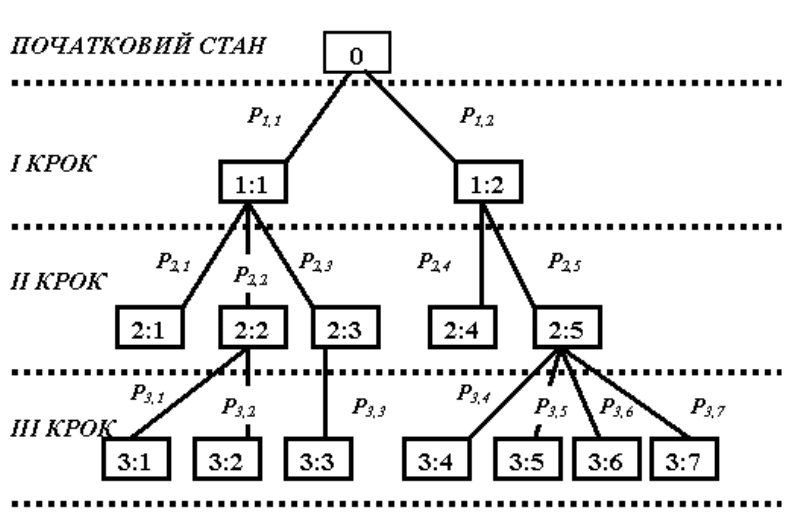
ОЗРАХУНОК ЙМОВІРНОСТЕЙ ПОДІЙ ЗА ДОПОМОГОЮ ГРАФІВ
МОЖЛИВИХ РЕЗУЛЬТАТІВ
В ряді випадків дослідження може бути представлене як
багатокроковий процес, в якому кожен попередній результат має декілька
наступних результатів.
В загальному випадку результати кожного кроку дослідження не
рівновірогідні. Подія, що цікавить дослідника, може відбутися після будь
якого кроку.
При великій кількості результатів та кроків звичайний підрахунок
імовірності події буде ускладнено. Такий процес можна спростити за
допомогою звичайного дерева-графа результатів.
Представимо результат умовного дослідження у вигляді графа:
Перший крок може мати два результати: (1:1) та (1:2) з відповідними
ймовірностями Р
1,1
та Р
1,2
. Кожен з цих результатів для другого кроку має
роль початкового стану. На другому кроці подія (1:1) може мати
результати (2:1), (2:2),(2:3) з відповідними ймовірностями Р
2,1
, Р
2,2
, Р
2,3
; а
подія (1:2) результати (2:4), (2:5) з відповідними ймовірностями Р
2,4
, Р
2,5
і
т.д.
Результати кожної події повинні створювати повну групу подій, що
підтверджують умови:
Р
1,1
+Р
1,2
=1
Р
2,1
+Р
2,2
+Р
2,3
=1; Р
2,4
+Р
2,5
=1
Р
3,1
+Р
3,2
=1; Р
3,3
=1; Р
3,4
+Р
3,5
+Р
3,6
+Р
3,7
=1
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
25
Повна імовірність кожного результату визначається як добуток всіх
ймовірностей, зазначених на відповідній гілці дерева, починаючи з даного
результату і закінчуючи коренем дерева (початковим станом).
3.5. Р
ОЗРАХУНОК ЙМОВІРНОСТЕЙ СКЛАДНИХ ПОДІЙ
,
ЩО
ПРЕДСТАВЛЕНІ У ВИГЛЯДІ КОМБІНАТОРНИХ ЕЛЕМЕНТАРНИХ ПОДІЙ
Складні події можуть бути представлені в вигляді комбінації
елементарних подій. В найбільш розповсюджених задачах складну подію
утворюють елементарні події, що відбуваються певну кількість разів, чи не
менше (не більше) певної кількості разів. Для розрахунків імовірності
складної події використовують формули суми та добутку подій, при
відповідній послідовності:
1. Складна подія записується у вигляді комбінації елементарних
подій, зв’язаних знаками суми та добутку.
2. Застосовуються формули імовірності суми та добутку подій.
3. Розраховуються імовірності елементарних подій (якщо вони не
відомі).
4. Підраховується імовірність складної події, що досліджується.
3.6. Ф
УНКЦІЯ РОЗПОДІЛУ ВИПАДКОВОЇ ВЕЛИЧИНИ
. Ч
ИСЛОВІ
ХАРАКТЕРИСТИКИ ВИПАДКОВИХ ВЕЛИЧИН
(
МОДА
,
МЕДІАНА
,
МАТЕМАТИЧНЕ
ОЧІКУВАННЯ,
СЕРЕДНЬОКВАДРАТИЧНЕ ВІДХИЛЕННЯ
,
ДИСПЕРСІЯ
,
КОЕФІЦІЄНТ ВАРІАЦІЇ
)
Функцією розподілу випадкової величини Х називається функція
F(x), що задає імовірність події, тобто імовірність того, що випадкова
величина Х буде менша за деяке число х:
F(x)=P{X
<
x}
Функція розподілу має наступні властивості:
1.
Функція F(x) неспадаюча функція: F(x
1
)
≥
F(x
2
) при x
1
>
x
2
2. Функція F(x) неперервна зліва:
);()(
lim
ε−=
−∞→
xFxF
x
(
ε>
0)
3. Функція F(x) прагне до нуля, якщо х прагне до -
∞
0
=
−∞→
)(lim
xF
x
4. Функція F(x) прагне до одиниці, якщо х прагне до +
∞
1
=
+∞→
)(lim
xF
x
Математичне очікування випадкової величини (як дискретної, так і
неперервної) - це те, до чого прагне її середнє значення при досить
великому числі спостережень.
Для дискретної випадкової величини: Mx =
∑
X
i
•
P(X
i
);
де P(X
i
) — імовірність того, що X прийме своє i-те чергове значення.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
26
Для неперервної випадкової величини:
∫
+∞
∞−
=
dxxxfMx
)(
Медіана (серединне значення) випадкової величини називається таке
значення випадкової величини X (позначається Me) при якому:
P(X
<
Me)=P(X
>
Me)=1/2
Для неперервної випадкової величини медіана знаходиться з умови:
F(Me)=1/2
Для дискретної випадкової величини медіана вираховується
неоднозначно та практично не використовується.
Мода (найбільш імовірне значення) випадкової величини
називається таке значення випадкової величини X (позначається Mо) для
якого у випадках дискретного розподілу імовірність Р(Х=Мо), а випадках
неперервного розподілу щільність імовірності F(Mo) має своє найбільше
значення.
Дисперсією випадкової величини називають очікування квадрата
відхилення значення величини від її математичного очікування:
Для дискретної випадкової величини:
P(Xi)
2
Mx)-(Xi =Dx •∑
Для неперервної випадкової величини:
∫
∞
∞−
•=
P(Xi)dx
2
Mx)-(XiDx
Розмірність дисперсії не збігається з розмірністю самої випадкової
величини і це не дозволяє оцінити величину розсіювання. Тому найчастіше
замість дисперсії використовується квадратний корінь з її значення —
середньоквадратичне відхилення чи відхилення від середнього значення:
Sx = Dx
Значення Mx і S
X
іноді не несуть повної інформації. Тому часто для
грубої оцінки "випадковості" величини використовують коефіцієнт
варіації чи відношення кореня квадратного з дисперсії до величини
математичного очікування:
V
x
= S
X
/M
X
3.7. З
АКОНИ РОЗПОДІЛУ ВИПАДКОВИХ ВЕЛИЧИН
(
ПАРАМЕТРИЧНА
СТАТИСТИКА
)
Закон розподілу випадкової величини - це ряд значень, які може
приймати ця випадкова величини. Тобто набір всіх допустимих її значень.
Закон розподілу випадкової величини вважається заданим, якщо:
1. Визначена множина можливих значень випадкової величини.
2. З'ясовано засіб кількісного визначення імовірності попадання
випадкової величини у довільній області цієї множини.
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
27
Встановити закон розподілу випадкової величини можна двома
засобами:
1. За допомогою експерименту побудувати схему випадкових події.
2. За допомогою аналізу властивостей випадкової величини,
визначити до якого з класичних законів розподілу відноситься ця
величина.
Хоча існує нескінченна множина випадкових величин, законів
розподілу набагато менше. Різні випадкові величини можуть мати
однаковий закон розподілу. Такі розподіли називають теоретичними, а їх
використання "параметричною статистикою". Для класичних законів
розроблені методи розрахунку всіх показників розподілу, зафіксовані
зв'язки між ними, побудовані алгоритми розрахунку і т.п.
Рівномірний закон розподілу
Неперервна випадкова величина X має рівномірний закон
розподілу, на відрізку [a, b], якщо щільність її імовірності f(x) постійна на
цьому відрізку і імовірність її попадання в будь-який відрізок у межі [a, b]
пропорційна довжині відрізка і не залежить від його положення, а
імовірність значень поза відрізком (а, b) дорівнює 0.
0; X
<
a
f(X)= 1/(b-a); a
≤
X
≤
b
0; X
>
b
Теорема. Функція розподілу випадкової величини X, розподіленої за
рівномірним законом є:
0; X
<
a
F(X)= (Х-а)/(b-a); a
≤
X
≤
b
1; X
>
b
Математичне очікування випадкової величини X, розподіленої за
рівномірним законом, дорівнює:
2
ba
XM
+
=)(
, а її дисперсія:
12
2
)(
)(
ab
XD
−
=
Нормальний закон розподілу
Неперервна випадкова величина X має нормальний закон
розподілу з параметрами а та
σ
, якщо щільність її імовірності f(x) має
вигляд:
ƒ
(x)=
2
2
2
2
1
σ
πσ
)(
ax
e
−
−
Теорема. Математичне очікування випадкової величини X,
розподіленої за нормальним законом, дорівнює параметру а цього закону,
а її дисперсія - квадрату параметра
σ
тобто : M(X)=a, D(X)=
σ
2
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
28
Біноміальний закон розподілу
Дискретна випадкова величина X має біноміальний закон
розподілу, якщо вона приймає значення 0, 1, 2, ..., m, ..., n з
ймовірностями:
nmm
n
qpCmXP
==
)(
де 0<p<1, q=1-p, m=0, 1, 2, ..., n.
)!(!
!
mnm
n
C
m
n
−
=
Біноміальний закон розподілу являє собою закон розподілу числа
X=m настання події A у n-незалежних спробах, у кожній з яких воно може
відбутися з однієї і тією ж імовірністю p.
Ряд розподілу біноміального закону має вигляд:
X
i
0 1 2 ... m ... n
P
i
q
n
11 −
n
n
qpC
222 −
n
n
qpC
...
mnmm
n
qpC
−
... p
n
Теорема. Математичне очікування випадкової величини X,
розподіленої за біноміальним законом дорівнює M(X)=np, а її дисперсія
D(X)=npq.
Геометричний розподіл
Дискретна випадкова величина X має геометричний закон
розподілу, якщо вона приймає значення 1, 2, ..., m, ... (нескінченна, але
рахункова множина значень) з ймовірностями:
P(X=m)=pq
m-1
де 0<p<1,
q=1-p,
m=1, 2, ...
Ряд геометричного розподілу має вигляд:
X
i
1 2 3 ... m ...
P
i
p pq pq
2
... pq
m-1
...
Очевидно, що імовірності P
i
утворять геометричну прогресію з
першим членом p і знаменником q (звідси і назва "геометричний
розподіл").
Визначення геометричного розподілу є коректним, оскільки сума
ряду
1
1
1
1
11
1
==
−
=++++=++++=
−−
∞
−
∑
p
p
q
pqqppqpqpp
mm
i
i
...)...(......
дорівнює одиниці.

Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
29
(
pq
1
1
1
=
−
є сума геометричного ряду
∑
∞
=
−
1
1
i
m
q
при |q|<1).
Випадкова величина X=m, що має геометричний розподіл, являє
собою число m спроб, проведених за схемою Бернулі, з імовірністю p
настання події в кожній спробі до першого позитивного результату.
Теорема. Математичне очікування випадкової величини X, що має
геометричний розподіл з параметром p дорівнює
,)(
p
XM
1
= а її дисперсія
дорівнює
,)(
2
p
q
XD
= де q=1-p.
Гіпергеометричний розподіл
Дискретна випадкова величина X має гіпергеометричний закон
розподілу, якщо вона набуває значення: 0, 1, 2, ..., min {n, M} з
ймовірностями
n
N
mn
MN
m
M
C
CC
mXP
−
−
==
)(
,
де m=1, 2, ..., min {n, M}, m≤N, n≤N; n, N, M - натуральні числа.
Теорема. Математичне очікування випадкової величини X, що має
гіпергеометричний розподіл з параметрами n, N, M, дорівнює
N
M
nXM =)(
,
а її дисперсія дорівнює
))(()(
N
n
N
M
M
N
nXD −−
−
= 11
1
Закон розподілу Пуассона
Дискретна випадкова величина X має закон розподілу Пуассона,
якщо вона приймає значення 0, 1, 2, ..., m, ... (нескінченна, але рахункова
множина значень) з ймовірностями
!
)(
m
e
mXP
m
λ
λ
−
==
де m=0, 1, 2, ...
Ряд розподілу закону Пуассона має вигляд:
X
i
0 1 2 ... m ...
P
i
e
-λ
λ
e
-λ
!
2
2
λ
λ
−
e
!
m
e
m
λ
λ
−
Визначення геометричного розподілу є коректним, оскільки сума
ряду
Конспект лекцій з дисципліни "Системний аналіз", укладач Добржанська О.Л.
30
1
2
1
2
2
2
0
=•=++++=
=−+++++=
−−
−−
−−
=
∑
λλλ
λλ
λλ
λλ
λ
λλ
λ
ee
m
e
m
ee
eep
m
m
n
i
i
)
!
...
!
(
...
!
...
!
дорівнює одиниці (в дужках записане розкладання в ряд функції e
x
при x=
λ
).
Теорема. Математичне очікування і дисперсія випадкової величини
X, розподіленої за законом Пуассона, збігаються і дорівнюють значенню
параметра
λ
цього закону, тобто
Mx=
λ
, Dx=
λ
Показовий (експонентний) закон розподілу
Неперервна випадкова величина X має показовий (експонентний)
закон розподілу з параметром
λ
, якщо щільність її імовірності f(x) має
вид:
0 при x<0,
f(x)=
λ
e
-
λ
x
при x>=0.
Теорема. Функція розподілу випадкової величини X, розподіленої
по показовому законі, є
0 при x<0,
f(x)=
1-e
-
λ
x
при x>=0.
її математичне очікування дорівнює
λ
1
=
Mx
, а її дисперсія
2
1
λ
=
Dx
Для випадкової величини, розподіленої за показовим законом,
математичне очікування дорівнює середньому квадратичному відхиленню,
тобто Mx=Sx
П
ИТАННЯ ДЛЯ САМОКОНТРОЛЮ
1. Дати визначення дискретних та неперервних величини. Навести
приклади.
2. Класифікувати випадкові події. Навести приклади.
3. Охарактеризувати поняття імовірність випадкової події. Навести
приклад.
4. Проаналізувати методи розрахунку імовірності випадкових подій.
5. Охарактеризувати поняття "математичне очікування випадкової
величини". Навести приклад.
