Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


11.1
f1
1
-Embeddings
in
Fixed Dimension
145
distance
d;
for this, one has to allow a residual 'split-prime'
term
in
the
decom-
position. We present here
the
main
ideas
and
results from
Bandelt
and
Dress
[1992]
that
we
need for our
treatment.
We do not give proofs as
this
would take
too
much space.
Let
d
be
a distance
on
V
n
.
Given two subsets
A,
B
<;;;
V
n
,
set
ood(A,
B)
:=
~
min
max(O, d(a,
b)
+ d(a',
b')
- d(a, a') - d(b, b'),
a,a'EA,
b,b'EB
d(a,
b')
+ d(a',
b)
- d(a, a') - d(b, b')).
(Here,
the
elements
a,
a' (or
b,
b')
may coincide.)
When
B =
Vn
\
A,
we
also set
The
quantity
ood(A)
is called
the
isolation index of
the
cut
semimetric 8(A)
(with
respect
to
the
distance d).
Then,
8(A) is
said
to
be a
d-splitif
ood(A)
>
O.
Clearly,
if
8(A)
is
a d-split
then
both
sets A
and
Vn
\ A are d-convex. (Recall Definition
4.2.7.) A
distance
d is said to
be
split-prime if d has no d-split.
In
general,
we
let
~d
denote
the
set
of
d-splits
of
d.
We
illustrate
the
definitions
on
some examples.
Example
11.1.8.
(i) Let d = 8(A)
be
a
cut
semimetric.
Then,
d
has
only one d-split, namely,
8(A) itself
with
isolation index
1.
(ii)
Let
d be a semimetric
on
4 points.
Then,
dis
f1
1
-embeddable. Moreover,
one
can
verify
that
d =
2:6(S)EE
d
ood(S)8(S).
(iii) Let d
:=
dT,w
be
the
path
metric of a weighted
tree
T = (V,
E)
with
nonnegative edge weights w. Recall
that
d can
be
decomposed as d =
2:eEE
w
e
8(Se)
where Se, V \
Se
denote
the
two
components
of
the
graph
T\e.
Clearly, every
cut
semimetric 8(Se) is a d-split
with
isolation
index
We
and
the
cut
semimetrics 8(Se)
(e
E
E)
constitute
all
the
d-splits.
(iv) Let
d
be
the
path
metric of
the
complete
bipartite
graph K2,3.
Then,
dis
split-prime
(as, for every set A, either A or its complement is not d-convex).
In
fact,
d(K
2
,3)
is
the
only (up
to
multiple) split-prime semimetric on 5
points
(Lemma
1
in
Bandelt
and
Dress [1992]).
There
are examples
of
split-
prime
distances
that
are
f1
1
-embeddable.
This
is
the
case, for instance, for
the
path
metric of
the
3-dimensional
hypercube
H(3, 2), or for
the
metric
on
5
points
d
:=
~(8(
{I,
4})
+8(
{I,
5})
+8(
{2, 4})
+8(
{2, 5})) (taking value
2
on
the
pairs (1,2)
and
(4,5)
and
value 1 elsewhere). I
Bandelt
and
Dress
[1992]
(Theorem
2)
show
that
every distance d on
Vn
can
be
decomposed as
(11.1.9)
d =
do
+ L ood(S)8(S),
6(S)EEd
where
do
is a split-prime distance
on
Vn
(that
is,
there
is no do-split)
and
the
sum
is
taken
over
the
set
~d
of d-splits;
do
is called
the
split-prime residue
of

146
Chapter
11.
Dimensionality
Questions
for
£l-Embeddings
d.
Moreover,
do
is a
semimetric
whenever d is a
semimetric.
The
decomposition
(11.1.9) is clearly unique.
It
can
be
found
in
time
O(n
6
).
The
collection
of
d-splits
has
some specific property. We need one
more
definition
in
order
to
formulate
it.
Call
a collection C
of
cut
semimetrics
on
Vn
weakly compatible
if
there
does
not
exist four
points
Xl,
X2, X3,
X4
E
Vn
and
three
cut
semimetrics
8(A
l
),
8(A
2
),
8(A3) E C whose
restrictions
on
the
set
X
:=
{Xl,
X2,
x3,
X4}
would
induce
the
three
distinct
cut
semimetrics
where
X is
partitioned
into two pairs.
In
other
words,
the
family C is weakly
compatible
if
and
only
if, for all
A,
B,
C E
C,
An
B n C
=1=
0
===}
A
~
B U
C,
or
B
~
AU
C,
or
C
~
AU
B (recall
the
definition
of
C from (11.1.2)).
One
can
verify
that
the
set
of
d-splits
of
a
distance
d is weakly
compatible.
Conversely,
we
have (from
Theorem
3
in
Bandelt
and
Dress [1992]):
Fact
11.1.10.
Let C
be
a weakly compatible family
of
cut semimetrics on
Vn
and let
>"s
> 0
be
given scalars for
8(8)
E
C.
Then, C is the set
of
d-splits
of
the
distance d
:=
I:8(S)EC
>"s8(8) and ctd(8) =
>..s
for all
8(8)
E
C.
I
As a consequence, every weakly
compatible
set
of
cut
semimetrics
on
Vn
is
linearly
independent
and,
thus,
has
cardinality::::;
G).
In
fact, for a
distance
d
having
a nonzero
split-prime
residue
do
in
(11.1. 9),
the
set
~d
U {
do}
is
linearly
independent.
A
distance
d
on
Vn
is
said
to
be
totally decomposable
if
d =
I:8(S)EE
d
ctd(8)8(8)
holds.
That
is, if
in
the
decomposition
(11.1.9)
there
is no
split-prime
residue,
i.e.,
do
=
o.
Then,
d is
£l-embeddable.
As
mentioned
in
Example
11.1.8 (ii),
every
semimetric
on
4
points
is
totally
decomposable.
In
general,
totally
decom-
posable
distances
are
characterized
by
the
following
5-point
criterion
(Theorem
6
in
Bandelt
and
Dress [1992]):
Fact
11.1.11.
A distance d on
Vn
is totally decomposable
if
and only if, for all
a,
b,
c,
d,x
E V
n
,
ctd({a, b}, {c, d}) = ctd({a,
b,x},
{c, d}) + ctd({a, b}, {c,
d,x}).
I
As
an
application,
one
can
check
total
decomposability
in
time
O(n
5
).
Finally
we
introduce
a
notion
of
minor
for distances. Let d
be
a
distance
on
V
n
,
let
do
be
its
split-prime
residue,
and
let
~d
be
its
set
of
d-splits.
Given
a
subset
X
~
V
n
,
a
distance
d'
on
X is
said
to
be
a minor
of
d
if
d'
is
of
the
form:
(11.1.12)
d'
=
>"od~
+ L >"s8(8 n
X),
8(S)EC
where
C
~
~d,
>"s
> 0 for
all
8(8)
E
C,
>"0
2:
0,
and
db
denotes
the
restriction
of
do
to
X.
Then,
the
d'-splits are
the
nonzero
cut
semimetrics
8(8
n
X)
for
8(8)
E
C.
(Here,
8(8
n
X)
denotes
the
cut
semimetric
on
X
determined
by
the
partition
of
X into
8nX
and
snx.)
In
other
words, a
minor
d'
of
d is
obtained
by
applying
the
following two
operations:
take
a
nonnegative
combination
of
the
d-splits
and
of
the
residue
of
d,
and/or
take
the
restriction
to
a
subset
X
of
the

11.1
£1
-
Embeddings
in
Fixed
Dimension
147
groundset
of
d.
Total
decomposability
is
obviously preserved by
taking
minors;
the
following
is
shown in
Bandelt
and
Dress
[1992]:
Fact
11.1.13.
A distance d is totally decomposable
if
and only
if
it
does
not
have the path
metric
of
the complete bipartite graph K
2
,3
as a
minor.
I
Examples
of
totally
decomposable distances include
path
metrics of weighted
trees
and
their
isometric subspaces, known as
tree
metrics.
In
other
words, a
distance
space
(X,
d)
is called a tree
metric
if
there
exists a
tree
T = (V,
E)
with
edge weights w E
R~
and
a
mapping
f : X
---+
V such
that
d(x,
y)
=
dT,w(f(x),f(y))
for
x,y
E
X.
Call two
cut
semimetrics 8(A)
and
8(B) crossing if
the
four sets
AnB,
AnB,
An
B,
An
Bare
nonempty
and
cross-free otherwise.
That
is, 8(A)
and
8(B)
are cross-free if two
of
the
sets A, ii,
B,
13
are comparable (for inclusion).
Then,
tree
metrics
admit
the
following characterization
2
:
Fact
11.1.14.
A distance d is a tree
metric
if
and
only
if
d is totally decompos-
able
and
any
two d-splits are cross-free. I
From
this
follows:
Fact
11.1.15.
Let
dl
and
d2
be
two tree
metrics.
Then,
their
sum
d
:=
dl +
d2
is totally decomposable with
set
of
d-splits
~d
=
~dl
U
~d2'
I
An
important
class of
totally
decomposable semimetrics is provided by
the
semimetrics
that
can
be
embedded
into
the
space
£7'
of
dimension m
:::;
2.
Indeed,
a
semimetric
that
can be
embedded
into £t is a tree metric (by
Lemma
11.1.3).
Hence, a distance
that
can be
embedded
into £i is
the
sum
of two tree
metrics
and,
thus, is
totally
decomposable.
This
fact will
playa
central
role for
the
recognition
of
£i-embeddable metrics, as
we
see in
the
next subsection.
11.1.3
Embedding
Distances
in
the
CrPlane
We
return
here
to
the
question
of
determining
the
order of congruence
h(m)
of
£7',
the
m-dimensional£l-space.
It
is
known
that
h(l)
= 4 (by
Theorem
6.2.13;
see also
Theorem
11.1.21).
It
is
not
known whether
h(m)
<
00
when m
2':
3.
Bandelt
and
Chepoi [1996a] have
computed
the
exact value of
h(2);
namely,
they
show
that
h(2)
= 6 (see
Theorem
11.1.24 below).
The
main
results
presented
here are Theorems 11.1.21
and
11.1.24 which give
several equivalent characterizations for £t-
and
£i-embeddability of a finite dis-
tance
space; in
particular,
in
terms
of
a list
of
forbidden
minimal
configurations.
We follow essentially
Bandelt
and
Chepoi [1996a] for
the
proofs.
2This
is
essentially
a
result
of
Buneman
[1971]
or,
independently,
Edmonds
and
Giles [1977],
which
shows
how
to
represent
cross-free families
of
cut
semimetrics
by
trees.

148
Chapter
11. Dimensionality Questions for i1-Embeddings
An
essential tool for these results is
the
theory of totally decomposable
distance spaces, exposed in the previous subsection. We will use in particu-
lar
the
properties of totally decomposable distance spaces, mentioned above
in
Facts 11.1.10-11.1.15.
\Ve
start
with several easy
but
crucial observations. As was observed
in
Lemma
11.1.3, a distance d can be embedded in the m-dimensional iI-space
(Jim, del)
if
and
only
if
d
has
a decomposition d 2::6(S)EC >'s8(8) (with
>'s
> 0
for all
8),
where C
can
be partitioned into m nested subfamilies.
In
the
case
m
=
1,2,
it
suffices,
in
fact,
to
check
this
property for
the
collection of d-splits.
Lemma
11.1.16.
A distance d
on
Vn
is if-embeddable
if
and only
if
d is totally
decomposable and its
set
:Ed
of
d-splits is nested. Then, d is the shortest path
metric
of
a weighted path.
Proof.
This
follows from
Lemma
11.1.3
and
the
fact
that
a nested family of
cut
semimetrics is weakly compatible. I
Lemma
11.1.17.
A distance d
on
Vn
is
iT
-embeddable
if
and only
if
d is totally
decomposable and its
set
of
d-splits can
be
partitioned into two nested fam-
ilies. Then, d can
be
isometrically embedded into the Cartesian product
of
two
Weighted paths.
Proof.
The
result follows using Fact 11.1.15
and
Lemma
11.1.16.
I
Lemma
11.1.18.
For m E {1,2},
if
dis
i'{'-embeddable, then so is every
minor
of
d.
Proof.
Suppose
that
d
is
il-
or iI-embeddable
and
let d'
be
a minor of d, say,
of
the
form (11.1.12).
Then,
d is totally decomposable,
that
is,
its
split-prime
residue
is
equal
to
zero. Hence,
d'
too is totally decomposable.
The
result now
follows using Lemmas
11.1.16
and
11.1.17. I
We
group
in
Theorem 11.1.21 several equivalent characterizations for
embeddability. One of
them
is in
terms
of
some distances
that
are forbidden
as minors;
they
are
the
path
metrics of
the
graphs K2,3, K3,
and
C
4
•
See
Figure
11.1.19 where are displayed the embeddings
in
the
il-plane
for
the
latter
two di'ltances.
Figure
11.1.19: Embedding K3
and
C4
in
the
iI-plane
(up
to
scale)

11.1 1\
-Embeddings
in
Fixed
Dimension
149
We
start
with
a
characterization
of
nested
families.
LeIllIna
11.1.20.
A
family
C
of
cut
semimetrics
is nested
if
and
only
if
every
subfamily
Co
<;;;
C with cardinality
ICo
I
::;
3 is nested.
Proof. We show
the
'if'
part
by
induction
on
the
cardinality
of
C.
We
suppose
that
ICI
:::::
4
and
that
every
proper
subset
of
C is nested; we show
that
C is
nested.
Let
8(
S)
E
C;
then,
the
elements
of
C \ { 8 (S)}
can
be
arranged
as
8(
AI),
...
,8(Am)
in
such
a way
that
Al C A2 C
...
C
Am.
If
SeAl
or
SeAl
then
C is nested.
If
S, S
rt.
Ai
for every i =
1,
...
,
m,
then
Am
C S (or
Am
C
S)
(because
the
three
cut
semimetrics
8(A
m
-
I
),
8(Am),
8(S)
form a
nested
family)
and
C is
again
nested. Else, let i
be
an
index
such
that
S,
S
rt.
Ai
and
S C Ai+!.
As
8(Ai),
8(Ai+l)
and
8(S)
form a nested family, we
obtain
that
Ai
eSc
Ai+l.
This
shows
that
C is nested. I
Theorem
11.1.21.
Let
d
be
a distance on V
n
.
The
following assertions are
equivalent.
(i)
(Vn,
d) is ft-embeddable.
(ii) d is totally decomposable
and
its
set
L;d
of
d-splits is nested.
(iii)
(X,
d) is ft-embeddable
for
every
subset
X
<;;;
Vn
such
that
IXI
::;
4.
(iv) d does
not
have as a
minor
the path
metrics
of
the
graphs K2,3, K3
and
C
4
•
Proof.
The
equivalence (i) ¢==;> (ii) holds
by
Lemma
11.1.16.
The
implication
(i)
===>
(iii) is obvious
and
(i)
===>
(iv) follows from
Lemma
11.1.18
and
the
fact
that
the
path
metrics
of K
2
,3,
K3
and
H(2,
2)
are
not
ft-embeddable.
We now show
the
implications (iv)
===>
(ii)
and
(iii)
===>
(ii). For this, we suppose
that
d does
not
satisfy (ii); we show
that
neither
(iii)
nor
(iv) holds.
If
d is
not
totally
decomposable,
then
d has
d(K
2
,3)
as a
minor
(by
Fact
11.1.15)
and
L;d is
not
weakly
compatible.
Hence,
there
exist
three
d-splits
8(A),
8(B),
8(C)
such
that
AnBnC
i=
0,
A
rt.
BUC,
B
rt.
AUC
and
C
rt.
AUB.
Let
Xl
E
AnBnC,
X2
E A
\BUC,
X3
E
B\AUC,
and
set
X:=
{Xl,X2,X3}'
Then,
(X,d)
is
not
ft-
embeddable
because
it
has
the
distance
8(AnX)+8(BnX)+8(CnX)
=
2d(K3)
as a minor.
We
can
now suppose
that
d is
totally
decomposable
and
that
L;d is
not
nested.
If
there
are
two crossing d-splits
8(A)
and
8(B),
then
we
can
choose four elements
Xl
E
An
B,
X2
E A n Ii,
X3
E
An
Band
X4
E A n
Ii.
Setting
X
:=
{Xl,
...
,X4},
the
distance
8(A
n
X)
+
8(B
n
X)
is a
minor
of
d
that
coincides
with
the
path
metric
of
H(2,
2); hence, (X,
d)
is
not
ft-embeddable.
Suppose
now
that
any
two d-splits
are
cross-free.
By
Lemma
11.1.20, we
can
find
three
d-splits
8(A),
8(B)
and
8(C)
which do
not
form a
nested
family. We
can
suppose
without
loss
of
generality
that
A C B (as
8(A)
and
8(B)
are
cross-free). As
8(C)
is cross-free
with
8(A),
we have A C C (or A C
C)
(as C, C
rt.
A,
else
8(A),
8(B),
8(C)
would form a
nested
family). Let
Xl
E
A,
X2
E B \ C
and
X3
E C \
B,
and

150
Chapter
11.
Dimensionality Questions for f1-Embeddings
X
:=
{Xl,X2,X3}.
Then, the metric
~(6(A
n
X)
+
6(B
n
X)
+ 6(C n
X))
on
X coincides
with
the
path
metric of
K3
and
is a minor of
d,
and
(X,d)
is not
£i-embeddable.
I
We now
turn
to
the
characterization of fi-embeddability.
We
start
with
establishing
an
analogue of Lemma 11.1.20 for 2-nested families of cut semimet-
rics.
The
result
3
from Proposition 11.1.22 will
playa
central role in the proof of
Theorem 11.1.24 below, which contains several equivalent characterizations for
fi-embeddable distances.
Proposition
11.1.22.
Let C
be
a family
of
cut semimetrics. Then, C can
be
partitioned
into
two nested families
if
only
if
the same holds for every subset
Co
of
C with cardinality
ICol
:::;
5.
Proof.
Let C be a family of cut semimetrics. An element 6(S) E C is said to be
extremal in C if one of S or S
is
minimal in C (i.e., if S
is
minimal
or
maximal
in
C).
Hence, 6(A)
is
not extremal if B
cAe
C for some
B,
C E
C.
Then,
we
say
that
6(A) separates 6(B) from 6(C).
We
show
the
'if'
part
in Proposition 11.1.22 by induction on
the
cardinality of
C.
So
we
can suppose
that
ICI
::::
6 and
that
every
proper
subset
of
C
is
2-nested.
Suppose, for a contradiction,
that
C is not 2-nested.
We
first show:
(a) There are
at
most four extremal elements in
C.
For, suppose
that
there are
five
extremal elements in
C.
By the assumption, they
can
be
partitioned into two nested families. Hence,
at
least three
of
them
form
a nested family, which contradicts the extremality assumption.
we
show:
(b)
For every extremal element 6(S) E
C,
the
family C \ {6(S)}
has no new extremal element.
Indeed, suppose
that
6(S) is
an
extremal element in C
and
that
6(T)
is
an
ex-
tremal
element
in
C \
{6(S)}
but
not in
C.
Consider a partition of C \ {6(S)}
into two nested families. Then, 6(S)
can
be
added to the nested family con-
taining
6(T), so
that
the new family remains nested. Hence, C
is
2-nested, in
contradiction with our assumption. This shows (b). From this
we
derive:
(c)
For every nonextremal element 6(A) E
C,
there exist four extremal
elements such
that
6(A) separates two of
them
from the other two.
This
follows from the fact
that
A contains at least two minimal sets
and
is
contained in
at
least two maximal sets from
C.
Indeed, if S is a minimal set from
~Pl'op'osi1;ion
11.1.22 is
an
analogue of
Lemma
11.1.20 for 2-nested families
of
cut
semimetrics;
it
was proved
by
Schrijver
[19951.
\Ve prefer
to
use
this
combinatorial result
rather
than
the
corresponding
result
given
in
Theorem
B from
Bandelt
and
Chepoi
[1996,,],
in
particular,
because
it
is
self-contained while
Bandelt
"nd
Chepoi
need
the
notion
of
median
graphs.
\Ve
thank
Lex
Schrijver for his
proof
of
Proposition
11.1.22.

11.1
fl-Embeddings
in
Fixed Dimension
151
C contained
in
A, then there exists a minimal set T
in
C \ {8, which is also
contained in
A. Now, T is also minimal in C because 6{T) is extremal
in
C by
(b). This shows (c).
Therefore, there are exactly four extremal elements in C (by (a) and (c)).
Say, they are
6{8;) for i
1,2,3,4,
where
8I,
82,
8
3
, 8
4
are minimal in
C.
By
(c), every nonextremal cut semimetric
6{A) separates two of
them
from
the
other
two.
This
makes three possibilities for such a separation.
We
first observe
that
not all three possibilities can occur simultaneously. For this, note
that
if 6{A) and 6{B) separate the extremal cut semimetrics
in
two distinct ways,
then
they are crossing. (Indeed, say 6{A) separates 6(8r), 6(8
2
) from 6(8
3
),
6(8
4
)
and
6{B) separates 6(8
1
),6(83) from 6(82),6(8
4
),
We
can
suppose
that
8
1
,82
cAe
53,5
4
,
8
1
,83 c B C 52,54. From
this
follows
that
A
ct
B,B
and
B,B
ct
A, i.e., 6{A)
and
6(B) are crossing.) Now, there cannot be three
pairwise crossing elements in C as they would form a family
that
is not 2-nested.
Hence,
at
most two possibilities can occur for the separation of the extremal
cut
semimetrics.
We
distinguish two cases.
Case
1: nonextremal cut semimetric 6(A) separates the extremal ones
in
the same way; say, it separates 6(8
1
),
6(82) from 6(83), 6(8
4
).
Consider a par-
tition of the nonextremal cut semimetrics into two nested families:
{6(Ad,
...
,
6(Am)}
and
{6(Bd,
...
, 6(Bp)}, where
Al
C
...
C
Am
and
B1
C
...
c
Bp.
We
can
always
add
the 6(8i)'S to either of these two nested families
so
as to retain
the
property of being nested. Indeed, say
Am
C
53,5
4
;
then, 8
1
,82
CAl'
Bp
C
S3,
and
8I,
8
2
c B
l
; then, 8
2
C
B1
C
...
c
Bp
C
54
and
CAl
C
...
C
Am
C 53. Or,
Bp
C 5
11
52
and
83,8
4
C B
1
; then,
we
can
add
8
4
to
the
chain
B1
C
...
C
Bp
and
8
1
,5
3
to
the
chain
Al
C
...
CAm.
Case
2: Every nonextremal
cut
semimetric separates, either 6(8
1
),
6(8
2
)
from
6(83),6(8
4
),
or
6(8
1
),0(8
3
)
from 6(8
2
),6(8
4
),
Let 6(A) satisfy the first possibil-
ity
and
6(B)
the
second one. Then, 6(A) and o(B) are crossing. Consider again
a
partition
of
the
nonextremal
cut
semimetrics into two nested families C
1
and
C
2
•
Say, o(A) E C
1
and
o(B) E C
2
•
Then, all elements of C
1
(resp.
C2)
separate
the
same two pairs of extremal cut semimetrics as o(A) (resp. o(B)). From this
follows
that
both
C
1
U
{6(8
2
),6(8
3
)}
and
C
2
U
{6(8d,6(8
4
)}
are nested.
C is 2-nested. This concludes
the
proof. I
The
following distances are not
fi
-embeddable: the
path
metrics of
the
graphs
K
2
,3,
K
5
, C5, C
6
(the circuits on 5
and
6 nodes), K2 x
Ka
(the Cartesian product
of
K2
and
K
3
)
(see Figure 11.1.23), as well as the four distances d
11
d2,
d3,
and
d
4
displayed in Figures 11.1.25-11.1.28. (We display there
an
embedding in
the
3-dimensional space for each of
the
distances.) (One
can
verify
that,
for each
of these distances,
their
set of d-splits cannot be partitioned into two nested
families.)
It
turns
out
that
these nine distances are
the
only minimal obstructions
to fr-embeddabilitYi this result is the contents of Theorem 11.1.24 below which
was proved by Bandelt
and
Chepoi [1996a].
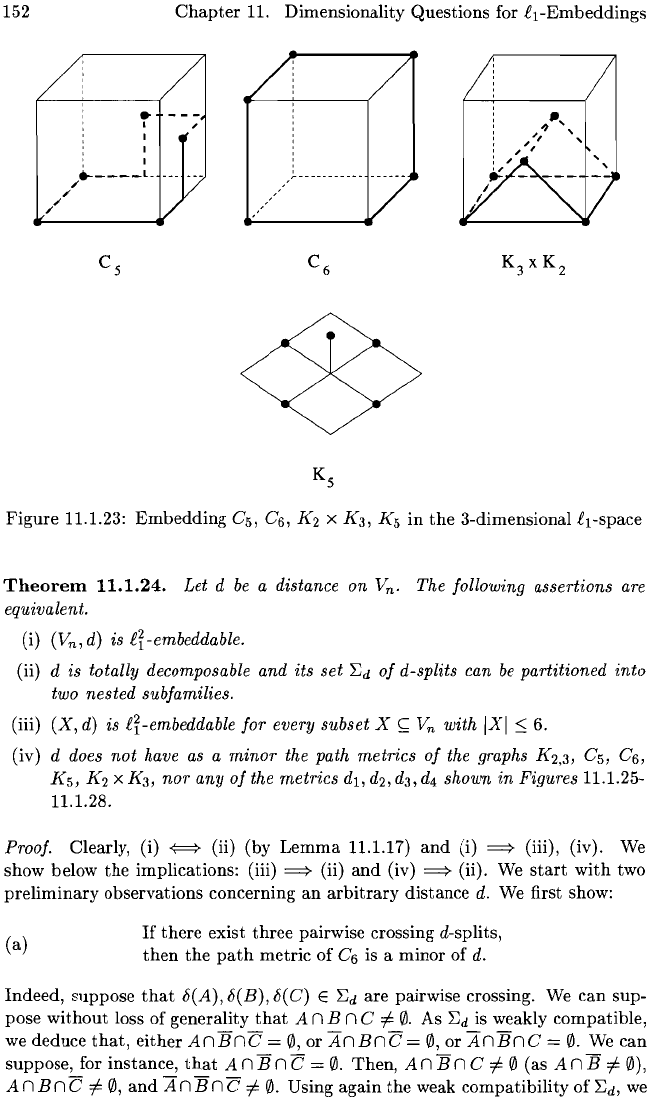
152
,,"
•
I
I
, I
Chapter
11.
Dimensionality
Questions
for
£l-Embeddings
•
____
L
_____
_
,
,
Figure
11.1.23:
Embedding
C
5
, C6, K2 X K
3
, K5
in
the
3-dimensional £l-space
Theorem
11.1.24.
Let d
be
a distance on V
n
.
The following assertions are
equivalent.
(i)
(Vn,
d)
is
£~-embeddable.
(ii) d is totally decomposable and its
set
~d
of
d-splits can
be
partitioned
into
two nested subfamilies.
(iii)
(X,
d)
is
£~-embeddable
for every subset X
~
Vn
with
IXI
:S
6.
(iv)
d does
not
have
as
a
minor
the path
metrics
of
the graphs K
2
,3,
C
5
, C6,
K5,
K2 X K
3
,
nor
any
of
the
metrics
dl,
d2,
d
3
,
d
4
shown
in
Figures 11.1.25-
11.1.28.
Proof. Clearly, (i)
~
(ii) (by
Lemma
11.1.17)
and
(i)
==>
(iii), (iv). We
show below
the
implications: (iii)
==>
(ii)
and
(iv)
==>
(ii). We
start
with
two
preliminary
observations
concerning
an
arbitrary
distance
d.
We first show:
(a)
If
there
exist
three
pairwise crossing d-splits,
then
the
path
metric
of
C6
is a
minor
of
d.
Indeed,
suppose
that
8(A), 8(B), 8(
C)
E
~d
are
pairwise crossing. We
can
sup-
pose
without
loss
of
generality
that
An
B n C
i=
0.
As
~d
is weakly
compatible,
we
deduce
that,
either
An:Bnc =
0,
or
AnBnC
=
0,
or
An:Bnc =
0.
We
can
suppose,
for
instance,
that
An:Bnc
=
0.
Then,
An:Bnc
i=
0 (as
An:B
i=
0),
An
B n C
i=
0,
and
An:B
n C
i=
0.
Using
again
the
weak
compatibility
of
~d,
we

11.1
ll-Embeddings
in Fixed Dimension
153
obtain
that
AnBnC
0 and, then,
that
:f.
0,
AnBnC:f.
0.
Pick an
element in each
ofthese
six sets:
Xl
E
AnBnC,
E
AnBnC,
X3
E
AnBnC,
X4EAnBnC,X5EA
C,andx6E
Bn
andsetX:={xl,
...
,X6}.
Then,
the
distance o(A n
X)
+ o(B n
X)
+ o(C n
X)
is a minor of d which co-
incides
with
the
path
metric of
the
6-circuit
C6
(Xl,
X3, X6,
X4, X5,
X2).
Hence,
(a) holds. Next,
we
show:
(b)
If
there
exist four d-splits O(Ai)(i =
0,1,2,3)
such
that
o(Ao)
and
o(A;) are crossing for i =
1,2,3
and A
1
,A2,A3 are all minimal in
{Ai,
Ai
I i = 1,2, 3},
then
the
path
metric of
C6
or
of
K2
x
K3
is
a minor of
d.
Indeed, suppose
that
such d-splits exist. Then, o(.4d,
O(A2)
and
O(A3)
are
pairwise cross-free (else,
we
are done in view of (a)). Hence,
Aln.42
Al
nA3
A
2
nA
3
= 0 (by
minimalityof
AI, A
2
,Aa)· Let
Xi
E
AonAi
and
Yi
E A;, for
i
1,2,3
(such points exist by assumption)
and
set X
:=
{Xi,Yi I i =
1,2,3}.
Then,
the
distance
o(Ao
nX)
+
~(2:1=1
o(A;
nX))
is a minor of d which coincides
with
the
path
metric of
K2
x K
3
•
This shows (b).
We
can now proceed
with
the
proof.
We
suppose
that
d does not satisfy (ii)
and
we
show
that
both
(iii)
and
(iv) are violated.
If
d is not totally decomposable,
then
we
are done. Indeed, d has
d(K
2
,3)
as a minor, which violates
both
(iii)
and
(iv). Suppose now
that
d is totally decomposable
and
that
:Ed
is not 2-nested.
By Proposition 11.1.22, there exists a subset
C
<;;;
:Ed
such
that
Ie!
:<:::
5
and
C is
not
2-nested. Choose such C
with
minimum cardinality.
We
distinguish three
cases.
Case
1:
ICI
3.
Then, any two members of C are crossing. By (a),
we
obtain
that
d(
C6)
is a minor of
d;
hence, (iii)
and
(iv) are violated.
Case
2:
ICI
4.
Suppose first
that
every member of C is cross-free with
at
least
another
member
of
C.
Let G denote the graph on
C,
where two elements
of
C are joined
by
an edge if they are cross-free. Then, G contains no matching
of size 2 (else,
C would be 2-nested). Moreover, the complement of G contains
no triangle (by the minimality of
C).
From this follows
that
G consists
of
a
triangle. Hence,
C {O(Ai) I i
0,1,2,
3}, where o(Ao) is crossing
with
O(Ai)
(i =
1,2,3)
and
the
o(A;)'s (i
1,2,3)
are
pairwise cross-free.
We
claim
that
the
set A {.4;,
IiI,
2,
3}
has three minimal elements
at
least. (For,
suppose
that
Al
and
A2
are the only minimal elements of
A.
Then, Al C A
2
,
A2
C and, for instance, C
.4,3,
A2
C A
3
•
This
implies
that
Al
C
.43
C A
2
•
Hence, C could
be
covered by two nested families, a contradiction.) Hence,
we
can
suppose
that
All
A2
and
are minimal elements of A. Applying (b),
we
obtain
that
d(K2 x Ka) is a minor of d and, thus, (iii)
and
(iv) are violated.
Case
3:
ICI
5.
Let H denote now the
graph
on
C,
where two elements are
joined by
an
edge if thay are
We
claim
that
the maximum degree of
a node
in
H is
:<:::
2.
Suppose first
that
there is a node of degree 4 in H; say,
o(As) E C is crossing with the four other elements O(Ai) (i =
1,2,3,4)
of
C.
The
o(Ai)'s
(i
=
1,2,3,4)
are pairwise noncrosssing and, for every i =
1,2,3,4,
the set
C \ {O(Ai)} is 2-nested (by the minimality of
C).
From this follows
that
the
family

154
Chapter
11. Dimensionality Questions for
il-Embeddings
C\
{8(~45),
8(Ai)} is nested for every i
1,2,3,4.
By
Lemma
11.1.20, this implies
that
C \
{8C45)}
is nested. Therefore, C
can
be
covered by two nested families, a
contradiction. Suppose now
that
H has a node of degree 3. Say, 8(A5) is crossing
with
8(A;)
(i
=
1,2,3)
and
cross-free
with
8(A4).
The
family C \ {8(A4)} can
be
covered by two nested families.
{8(Ad,
8(A2), 8(A3)}
is
nested and,
thus,
C
can
be
covered by two nested families, a contradiction. So,
we
have shown
that
the
maximum
degree in H
is
::;
2.
Therefore, H
is
either a circuit on 4 or 5
nodes, or a disjoint union of paths. For every
8(.4;)
of
degree
at
most 1 in
H,
we
can
select a point from Ai
that
does not belong
to
the
other
A/s.
Moreover,
we
can select a point in every nonempty intersection
Aj
n Ak, where
at
least one
of
8(Aj) and 8(Ak)
has
degree 2 in H. Altogether
we
have selected a set X
of
five
or six points such
that
the
family {Ai n
X,
Ai
n X
IiI,
2,
3, 4,5} has
at
least
five minimal members. Hence,
the
family {8(Ai n
X)'I
i =
1,2,3,4,
5}
cannot
be
covered
with
two nested families and, thus, (X,
d)
is not if-embeddable.
We
list below
the
possible configurations for
the
graph
H together
with
the
corresponding distance
dH
:=
L:f=18(Bi) on
X,
setting Bi
:=
Ai
n
X.
In
each
case,
we
find one of
the
forbidden distances as a minor.
(i)
When
H
then
BI {1,2},
B2
= {2,3},
B3
= {3,4},
B4
= {4,5},
and
Bs {5, I}. Hence,
dlI
is (up
to
a factor
2)
the
shortest
path
metric
of
0
5
•
(ii)
When
H is the disjoint union of PI and two
paths
P
2
,
then
Bi =
{i}
for
i 1,
...
,5. Hence,
dlI
is (up to a factor
2)
the
path
metric of
the
complete
graph
Ks.
The
remaining cases are displayed in Figures 11.1.25-11.1.28. (We show
an
em-
bedding
of
the
distance in
the
3-dimensional grid, as well as the sets Bi.) I
o
4
D
H
Figure 11.1.25: H 0
4
,
distance dl
