Deza M.M., Laurent M. Geometry of Cuts and Metrics

134

Chapter

10. Lipschitz

Embeddings

theorem

by Ford

and

Fulkerson [1962].

In

the

case k = 2

this

is

the

max-flow

min-cut

theorem

for two commodities, proved by

Hu

[1963].

These

two

results

can

also

be

derived from some

properties

of R1-embeddings; see Corollary 10.3.7

below.

For

an

arbitrary

number

k of

commodity

pairs,

the

max-flow is

in

general

less

than

the

min-cut.

However,

the

gap

between

the

max-flow

and

the

min-cut

cannot

be

too

big.

The

first

result

in

this

direction is

due

to

Leighton

and

Rao

[1988], who proved

that

the

ratio

p:=

.

cap(S)

mln---

s~v

dem(S)

).*

is O(log n) in

the

case

when

all

demands

are one

and

there

is a

commodity

between

any

pair

of

vertices, i.e., k =

G).

Several

improvements

of

this

result

have

been

proposed

thereafter,

in

particular,

by Klein, Agrawal, Ravi

and

Rao

[1990],

Plotkin

and

Tardos

[1993]' Garg, Vazirani

and

Yannakakis [1993].

The

best

result

is due

to

Linial,

London

and

Rabinovich [1994],

who

proved

that

p = O(log k) for

arbitrary

demands

and

capacities

and

an

arbitrary

number

k

of

commodity

pairs; see

Theorem

10.3.3

2

below.

This

result is

based

on

the

results

from

Theorems

10.1.2,10.1.6

and

10.1.7.

Theorem

10.3.3.

constant. Moreover,

polynomial time.

.

cap(S)

We have:

mm

-d

(S)::;

(co

log

k)'*,

where

Co

> 0 is a

s~v

em

a subset S for which

~:;:,W)

::;

(cologk)'*

can

be

found

in

Proof. We

remind

that

).*

is

the

optimum

value of

the

linear

program

(10.3.1).

Applying

the

linear

programming

duality

theorem,

we

obtain:

(10.3.4)

).

* =

min

L Cez

e

eEE

L Ze

~

Yh

eEP

2..=

DhYh

~

1

lShSk

Yh

~

0

Ze

~

0

(P E

Ph,

h = 1,

...

,k)

(h

= 1,

...

,k)

(e

E E).

Let

(y,

z)

be

an

optimum

solution

to

the

program

(10.3.4).

We

can

suppose

that

Ze ::;

2.,jEP

Zj

for every edge e =

ij

of G

and

every

path

P from i

to

j

in

G. (For,

if

not,

replace Z by z' where, for

an

edge e =

ij

of

G,

z~

:=

min(ze,

2.,jEP

Zj

for P

path

from i

to

j in G).) Let d

z

denote

the

shortest

path

2 A

randomized

version

of

Theorem

10.3.3

appeared

in

the

earliest version

of

Linial,

London

and

Rabinovich

[1994].

This

randomized

version was

independently

obtained

by

Aumann

and

Rabani

[1997].

Garg

[1995a]

has

also

derandomized

the

randomized

version from Linial,

London

and

Rabinovich

[1994]

and,

thus,

obtained

Theorem

10.3.3.

10.3

An

Application for Approximating Multicommodity Flows

135

metric of

the

weighted

graph

(G,

z)

(where, for

i,j

E V,

dz(i,j)

is defined as

the

smallest value

of

L Ze taken over all

paths

P from i to j in G). Then,

eEP

.\

* = L Gez

e

?:

--;-"-"'--'---'----

eEE

semimetric d on V, set Ze

1.

On

the

other

hand,

given a

=:-;:---":.=.1.'---

for

an

edge e =

ij

in G

and

Yh

:=

Dhd(Sh,thl

1,

...

,k.

Then,

(y,

z)

is feasible for

the

program (10.3.4),

2:ijEE Gijd(i,j)

2:Ll Dhd(Sh, th)

This

shows, therefore,

that

.\ * can

be

reformulated as

.

2:ijEE

Gijd(i,j)

mm

k .

d semimetric

on

V 2:h=I Dhd(Sh, th)

(10.3.5)

.\*

Let d

be

a semimetric on V.

If

d happens to

be

a

cut

semimetric

8(8),

then

2:ijEE G;jd(i,j)

cap(8)

2:~=I

Dhd(Sh, th) =

dem(8)'

More generally,

if

d is isometrically t'I-embeddable,

then

d = 2:s .\s8(8) for some

.\s

?:

0, which implies

that

2:ijEE Gijd(i,j)

2:s

.\scap(8)

.

cap(8)

2:~=1

Dhd(Sh, th) =

2:s

.\sdem(8)

2:

mJn

dem(8)'

In

general, d is

not

isometrically t'I-embeddable. However, by

Theorem

10.1.6,

there exist a

constant

CO

and

vectors

Wi

E

jiK

(i

E

V)

such

that

(10.3.6)

{

II

Wi

-

Wj

IiI

~

d(i,j)

d(Sh, th)

:::;

(CO

log

k)

II

W

Sh

Wth

IiI

(We

apply

Theorem 10.1.6 with X = V

and

Y

Therefore,

for all

i,j

E

V,

for

hI,

...

,k.

1,

...

,k}.)

(using

the

argument above). This shows

that

.\ *

2:

mins

A subset 8 realizing

~:\~)

~

(co

log k)'\" can

be

constructed in

the

following

way.

In

view of (10.3.5),

the

max-flow .\* can

be

found by solving

the

linear

136

Chapter

10.

Lipschitz Embeddings

program:

A*

min

L

Cijd(i,j)

ijEE

k

L Dhd(Sh' th) = 1

h=l

d semimetric on

V.

which

can

be clearly done

in

polynomial time. Let d be an optimum solution.

By Theorem 10.1.7,

we

can

find vectors

Wi

= (wi(r»)f=l E

~K

(i E

V)

satisfying

(10.3.6)

and

with K O(n

2

).

Determine the coordinate index r E K for which

the

quantity

is minimum.

The

semimetric

d(r)

on V defined

by

d(r)(i,j)

:=

IWi(r)

- wj(r)1 for

i,j

E

V,

is iI-embeddable by construction. Hence,

d(r)

L AA6(A) where

AA

> 0 for

AEA

A E A. Such a decomposition can be easily found; recall, e.g., Proposition 4.2.2

d

. f

Th

A A

1"

. cap(A) .

fi

h'

l'

an

Its proo . en, a set 0 E rea Izmg

mm

d (A)

sabs

es t e mequa Ity:

AEA

ern

~:~~~~))

::;

(co

log k)A

*.

Indeed,

we

have:

I

Corollary

10.3.7.

For the case

of

k

::;

2 commodity pairs, max-flow min-cut,

i.e.,

A*

= min cap(S) .

s<;v

dem(S)

Proof.

We

use the proof of Theorem 10.3.3. Let d be a semimetric on V which is

an

optimum

solution for the program (10.3.5). Suppose first

that

k 1. Define

the semimetric

d' on V

by

setting

d'(i,j)

:=

Id(i, sd -

d(j,

sdl

for

i,j

E V.

Then,

d(i,j)

?:::

d'(i,j)

for all

i,j

E V

and

d'(s!,

td

=

d(Sl,

tl)'

Hence,

LijEE

Cijd(i,j)

LijEE

Cijd'(i,j)

k > k •

Lh=l

Dhd(Sh' th) -

Lh=l

Dhd'(Sh, th)

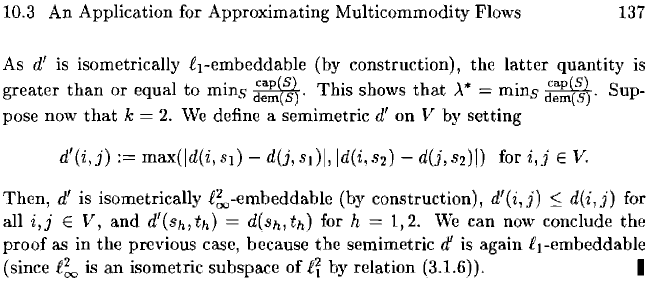
10.3 An Application for Approximating Multicommodity Flows

137

As

d'

is

isometrically iI-embeddable (by construction), the

latter

quantity is

greater

than

or equal to mins This shows

that.\*

mins

~:;;.~~).

Sup-

pose now

that

k =

2.

We

define a semimetric

d'

on V by setting

Then,

d'

is

isometrically

i~-embeddable

(by construction),

d'(i,j)

:;

d(i,j)

for

all

i,j

E

V,

and

d'(Sh,th) = d(Sh,th) for

It

1,2.

We

can now conclude the

proof as in the previous case, because

the

semimetric

if

is

again iI-embeddable

(since

.e~

is

an

isometric subspace

of

iy

by relation (3.1.6)). I

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,

DOI 10.1007/978-3-642-04295-9_11, © Springer-Verlag Berlin Heidelberg 2010

Chapter

11.

Dimensionality

Questions

for

ll-Embeddings

Given a distance space (X,

d)

which

is

R1-embeddable, a

natural

question is

to

determine

the

smallest dimension m of

an

Rl-space Rl' =

(I~m,

del) in which

(X,

d)

can

be embedded. A

point

criterion

for Rl'-embeddability, analogue

to

Menger's result for

the

Euclidean space;

this

is

the

question of finding

the

order of congruence of

fl'.

We present

in

this

chapter

several results related

to

these questions. Unfortunately fairly little

is

known. For

instance,

the

order

of congruence

of

Rl' is known only for m

:::;

2

and

it is

not

even

known

whether

Rl' has a finite order

of

congruence for m

:::::

3.

More precisely, a

distance space

(X,

d)

is

Ri-

(resp. Ri-embeddable) if

and

only if

the

same

holds

for every subspace of

(X,

d)

on 4 (resp. on

6)

points. As a consequence, one

can

recognize in polynomial

time

whether a distance

is

Rl'-embeddable for m

:::;

2.

On

the

other

hand,

the

complexity

of

checking Rl'-embeddability

is

not known

for m

:::::

3. These results are presented

in

Section 11.1. A crucial tool for

the

proofs is

the

notion

of

'totally

decomposable distance'

studied

by

Bandelt

and

Dress [1992]; Section 11.1.2 contains

the

facts

about

total

decomposability

that

are needed for

our

treatment.

Then

we

consider

in

Section 11.2 some

bounds

for

the

minimum

Rp-dimension

of

an

arbitrary

Rp-embeddable distance space

on

n points.

11.1

£l-Embeddings

III

Fixed

Dimension

Let us begin

with

several observations concerning

the

structure

of

Rl'-embeddable

distances, where m

:::::

1

is

an

integer. Let

(Vn'

d)

be

a distance space which is

R1-embeddable.

Then,

d

admits

a decomposition as

(11.1.1)

d

= L >'s8(8),

8(S)EC

where

>'s

> 0 for all 8(8) E C

and

C is a family

of

cut

semimetrics on V

n

.

When

d

is Rl'-embeddable

then

d has such a decomposition which has a special

structure.

We need some definitions in

order

to

formulate it.

Given a family C

of

cut

semimetrics on V

n

,

set

(11.1.2)

c:=

{8, S

:=

Vn

\

818(8)

E

C};

the

members

of

C are called

the

shores

of

the

cut

semimetrics

in

C.

The

family C

140

Chapter

11. Dimensionality Questions for e

1

-Embeddings

is said

to

be

nested

if

the

elements of C

can

be

ordered

as

Sl,

...

,

Sm,

51,

...

,5

m

in

such

a way

that

Sl

c S2 C

...

C

Sm

(and, thus, 5

m

C

...

C

52

C

5d.

Given

an

integer m

2:

1,

C is

said

to

be

m-nested

if

C

can

be

partitioned

into

m

nested

subfamilies. (Hence,

I-nested

means

nested.)

We have

the

following (easy)

characterization

for

el-embeddability;

it

was

in

fact

already

contained

in

Proposition

4.2.2

but

we

recall

it

here for clarity.

Lemma

11.1.3.

Let

(Vn' d)

be

a distance space.

The

following

assertions

are

equivalent.

(i) (Vn, d) can

be

embedded

into

el.

(ii) d

admits

a decomposition (11.1.1) where C is

m-nested.

(iii) (Vn' d) can

be

isometrically

embedded

into

the

Cartesian

product

of

m

weighted paths.

Proof.

We first consider

the

case

when

m =

1.

(i)

===}

(ii), (iii).

Suppose

that

d is

et-embeddable.

Then,

there

exist scalars

U1,

...

,Un

such

that

dij =

lUi

-

Ujl

for all

i,j

E V

n

. Up

to

a reordering of

the

elements

of V

n

,

we

can

suppose

that

U1

~

U2

~

...

~

Un.

Then,

n-l

d = 2.)

Ui+1

-

ui)5(

{I,

...

,i}).

i=l

Then,

(ii) holds as

the

family {5({I,

...

,i})

Ii

= I,

...

,n

-I}

is obviously

nested.

Consider

the

path

P = (1,

...

, n)

with

weight

Wi,i+1

:=

Ui+1

-Ui

on

edge

(i, i + 1) (i = 1,

...

, n - 1).

Then,

the

shortest

path

metric

of

the

weighted

path

P coincides

with

d,

which shows (iii).

(iii)

===}

(ii).

Let

P = (1,

...

, n)

be

a

path

with

nonnegative weight

Wi

on

edge

(i, i + 1) for i = 1,

...

,n

- 1.

Then,

its

path

metric

dp,w

can

be

decomposed as

L:;';:"l

w

i

5(

{I,

...

, i}).

(ii)

===}

(i).

Suppose

now

that

d =

L:f=l

Qi5(Si), where

Qi

> 0 for all i

and

Sl

C

S2

...

C Sp. Define

U1,

.

..

,

Un

E

lR

by

setting

Ui:=

0

Ui

:=

L:~=1

Qh

Ui

:=

L:~=1

Qh

for i E S1,

for

i E Sk+1 \

Sk,

k = 1,

...

,m

- 1,

for

i E

Vn

\ Sp.

Then,

one

can

verify

that

dij =

Uj

-

Ui

for all

i,j

E V

n

, which shows

that

dis

et-embeddable.

The

result

for m

2:

2 follows now easily using additivity, since d is

el-embeddable

if

and

only

if

d

can

be

decomposed as a

sum

d = d

1

+ ... + d

m

,

where all di's

are

et-embeddable.

I

It

is

not

clear how

to

use

this

result for devising a

polynomial

algorithm

permitting

to

recognize

el-embeddable

distances.

The

difficulty is

that

a dis-

tance

in

the

cut

cone

CUTn

has

many

decompositions as (11.1.1) (in fact,

an

11.1

fl-Embeddings

in Fixed Dimension

141

infinity, if

it

is

not

fl-rigid). However, as

we

will see in Section 11.1.3 below, in

the

cases m = 1,2,

it

is enough

to

check one special decomposition (namely, the

one corresponding to a

'total

decomposition' of

d).

In

particular, one can check

embeddability in

the

space f'{' for m E

{I,

2}

in polynomial time. Moreover, one

can

determine

the

order of congruence of

fi.

These results need the notion

of

total decomposability for their proofs.

So

we

organize

the

rest of

the

section in the following manner.

We

summarize in Section

11.1.1 what is known about the order of congruence of the space

f'{' as well as

some results on

the

iI-dimension of some specific distance spaces. Then, after

introducing in Section 11.1.2

the

definitions and facts about totally decomposable

distances

that

we

need for our treatment,

we

present in Section 11.1.3 the proofs

for

the

results concerning embeddability in the iI-space of dimension

m::;

2.

lL1.1

The

Order

of

Congruence

of

the

l\-Space

Let fp(m) denote

the

order of congruence of

f;';

that

is, fp(m) is the smallest

integer such

that

an

arbitrary

distance space (X,

d)

is

f;'-embeddable if

and

only

if every subspace of

(X,d)

on fp(m) points

is

f;'-embeddable. By convention,

we

set fp(m) =

00

if fp(m) does not exist.

We

remind from Theorem 3.2.2

that

we

may restrict our attention to finite distance spaces

(X,

d).

The

study

of the parameter fp(m) is motivated by the result of Menger in

the case

p

2,

quoted in Theorem 6.2.13. Namely, Menger

[1928]

showed

that

a distance space

(X,

d)

embeds isometrically in the Euclidean space

(lltm,

d(2)

if

and

only if each subspace of

(X,

d)

on m + 3 points embeds isometrically in

(JR(m,

d

(2

).

In

other

words,

hem)

=

m+

3 for each m

~

1.

Hence,

we

have the

natural

question of looking for analogues of Menger's theorem

for

the

case of arbitrary ip-metrics and, in particular, in the case p =

1.

This

turns

out

to

be a difficult question. Only

the

following partial results are known.

Since

the

spaces (lit,

d£p)

and

(lit, df2) are identical,

we

deduce from Menger's

theorem

that

fp(l)

= 4 for all p. (See also Theorem 11.1.21 for a direct

proof

of

the

fact

that

h(l)

4.) Malitz

and

Malitz

[1992]

show

that

6::;

h(2)

::;

11

and

hem)

~

2m + 1 for all m

~

1.

These results are improved by Bandelt

and

Chepoi

[1996a]

who show

that

h(2)=6

and

by Bandelt, Chepoi

and

Laurent

[1997]

who show

that

hem)

~

m

2

for m

~

3 odd,

hem)

~

m

2

-

1 for m

~

4 even.

The

equality: h (2) 6 will

be

proved in Theorem 11.1.24 and the inequalities:

hem)

~

m

2

for m odd,

hem)

~

m

2

1 for m even, are given in Corollary 11.1.6

below. Malitz and MaUtz

[1992]

conjecture

that

hem)

is

finite for all m.

142

Chapter

11.

Dimensionality

Questions

for

f1-Embeddings

In

view

of

the

above

mentioned

results, one

can

test

in

polynomial

time

whether

a given finite

distance

space

(X,

d)

embeds

in

(JF.

m

,

del)'

when

m = 1

or

2.

(The

case m = 1 is anyway easy, as

del

and

d

e2

coincide

when

restricted

to

:IF..)

It

would

be

very

interesting

if

one could show

that

h (m) is finite for

all

m.

Indeed,

this

would

imply

the

existence

of

a

polynomial

time

algorithm

for checking

embeddability

of

a finite

distance

space

in

the

space

(JF.

m

,

del)' for

any

given

m.

The

complexity

of

the

embedding

problem

into

(JF.

m

,

del) for some

fixed

m

::::

3 is

not

known. We recall

that,

on

the

other

hand,

checking f

1

-

embeddability

of

a finite

distance

space (i.e.,

embeddability

into some

(JF.

m

,

del)

for

unrestricted

m) is

NP-complete

(cf. Section 4.4).

We conclude

this

section

with

some

remarks

on

the

f1-dimension

of

some

concrete

examples

of

distance

spaces. We

remind

that

mel (X,

d)

denotes

the

smallest

m

such

that

(X,d)

can

be

embedded

into

fl'

This

parameter

can

be

easily

formulated

in

the

case

of

f1-rigid metrics.

Indeed,

if

(X,

d)

is

an

f1-rigid

distance

space,

then

it

has

a unique

decomposition

as (11.1.1)

and,

therefore,

mel (X,

d)

is

equal

to

the

smallest

number

of

nested

families needed

to

cover

the

set

C

of

cut

semimetrics

entering

in

this

decomposition. For

instance,

hypercube

embeddable

graphs

have

their

path

metric

which is f1-rigid.

In

particular,

trees

are

hypercube

embeddable

and,

thus,

f1-rigid. (See

Proposition

19.1.2.) We now

give some

more

details

about

trees

as

they

will play some role here;

justification

for

the

facts

quoted

below

can

be

found

in

Section 19.1.

Let

T = (V,

E)

be

a tree. Every edge e E E

determines

a

partition

of

the

node

set

V into two

sets

Se

and

V \ Se.

Then,

the

path

metric

of

T

can

be

decomposed

as

dT

= L o(Se)

eEE

and

this

is

its

only Rt--realization. More generally,

if

w E

JF.~

are weights as-

signed

to

the

edges

of

T,

then

the

path

metric

dT,w

of

the

weighted

tree

can

be

decomposed

in

a

unique

way as

dT,w

= L weo(Se)'

eEE

One

can

easily

determine

the

f1-dimension

of

a

tree

in

terms

of

its

number

of

leaves

1

.

The

was

already

formulated by Hadlock

and

Hoffman [1978].

Proposition

11.1.4.

The following assertions are equivalent

for

a tree

T.

(i) The path

metric

of

T can

be

embedded

into

fl'

(ii) T can

be

covered by m paths.

(iii) T has at

most

2m

leaves.

Therefore,

if

T has p leaves,

then

the f1

-dimension

of

its path

metric

is equal to

m·

1 A

node

v

of

T is a

leaf

if

its

degree

is

equal

to

1.

11.1

il-Embeddings

in

Fixed Dimension

143

Proof. Let T (V,

E)

be a tree and, with the above notation, let

CT

:=

{8(Se)

I

e E

E}

denote the family

of

cuts entering the decomposition

of

dT. Then, (i)

can

be

equivalently formulated as: (iv)

The

family

CT

is m-nested.

We show

the

equivalence

of

(ii)-(iv).

The

implications (ii)

=*

(iii), (iv) are clear.

For (iv)

=*

(iii), suppose

that

T has

at

least 2m + 1 leaves. Then, there are

at

least

2m

+ 1 minimal sets

in

C (as each leaf v yields the minimal set {v}).

Hence, C cannot

be

covered

with

m nested families.

The

implication (iii) (ii)

can

be shown by induction on m

~

1.

We

leave the

details to the reader.

I

In

order to lower bounds for the order

of

congruence

h(m),

we

need as

a tool

the

following result

about

the

iI-dimension

of

a direct product

of

distance

spaces.

Lemma

11.1.5.

Let

(XI,dd,

(X2,d2)

be

two distance spaces

and

let

(X,d):=

(Xl

X X

2

,

dl

(13

d2)

be

their

direct product.

Then

the following relation holds:

m£l(X,d)

mel(XI,dd

+mel(X2,d2).

Proof.

The

inequality;

mel

(X,

d)

:S:

mel

(Xb

dd+mil

(X2'

d2)

follows by additiv-

ity

of

the iI-distance. Conversely, suppose

that

(X,

d)

embeds

in

ii.

Then,

dean

be

decomposed as d = L:8(S)EC A

s

8(S),

where C

is

a family of cut semimetrics on

X

that

is

m-nested. By the proof

of

Proposition 7.5.2,

we

know

that

every

cut

semimetric in

Cis

of

the form

8(A

x X

2

) or 8(XI X

B)

for

some A C

Xl,

B C X2.

Say, d = L:AEA AA8(A x X

z

)

+ L:BEB A

B

8(XI

X

B).

Then, d

l

=

I:AEA

AA8(A)

and

d

z

L:BEB

AB8(B).

Note

that

no

two cut semimetrics

8(A

x X

2

)

and

8(XI x

B)

can

be

put

together

in

a nested family. Hence, the m nested families

partitioning

C yield a

partition

of

the

cut semimetrics

8(A)

(A

E

A)

in p nested

families

and

a

partition

of

the

cut

semimetrics

8(B)

(B

E

B)

in q nested families

with

p + q = m. Therefore, p

~

mil

(Xl,

dd

and q

~

mil

(X2'

d

2

),

which implies

the

converse inequality;

mil(X,d)

~

mil(XI,d

l

)

+mel(X

2

,d2).

I

Corollary

11.1.6.

hem)

~

m

2

for

m odd;

h(m)

~

m

2

1

for

m even.

Proof.

We

start

with

an

observation. Let

(X,

d) denote the graphic metric

space of

the

graph G

:=

KI,s x KI,t (the Cartesian product of the two complete

bipartite

graphs KI,s

and

KI,t) where s, t

~

3.

Its

ii-dimension is

mil

(X,

d)

r~l

+

r~l

(applying Proposition 11.1.4 and Lemma 11.1.5, as KI,Sl KI,t are trees

with

s and t leaves, respectively). Say, G has node set X

VI

x

V2,

where

VI

:=

{UO,UI,

...

,U

s

}

and V

2

:=

{vo,Vl,

...

,Vt} (uo,vo denoting the respective

'centers' of

the

stars

KI,s

and

KI,t).

Then,

d can be decomposed as

d=

8(Si)

+

8(Tj),

setting

Si

:=

{'Ui}

xV

2

(i

1,

...

, s)

and

Tj

VI

x {Vj}

(j

1,

...

,t). Clearly, no

144

Chapter

11. Dimensionality Questions for i'l-Embeddings

two

cut

semimetrics

8(8i),

8(Tj)

form a nested pair, while any two 8(8i),

8(8

j

) (or

8(n),

8(Tj))

do form a nested pair. This shows again

that

mi,

(X,

d)

=

r~l

+rn

On

the

other

hand, if

we

delete the element x

:=

(Uio,

Vjo)

from X (where

io E {I,

...

, s}

and

io E {I,

...

, t} correspond to leaves in

the

two trees),

then

the two

cut

semimetrics 8(8;0 \

{x})

and

8(T

jQ

\

{x})

become a nested pair.

Hence, one

can

now

partition

the

cut

semimetrics 8(8; \

{x}),

8(Tj

\

{x})

into

r~l

+

r~l

- 1 nested subfamilies, which shows

that

(a)

for such

x.

We

can

now proceed

with

the proof.

We

first show

that

h(m)

.?:

m

2

for m

odd. For this,

it

suffices to construct a distance space

(Y,

d)

such

that

WI

.?:

m

2

,

me, (Y,

d)

.?:

m + 1

and

mi,

(Y

\ {y},

d)

::;

m for all y E

Y.

Namely, let

(X,

d)

be the graphic metric space of the graph

K1,m

X

K1,m,

with

mi,

(X,

d) = m +

1.

Let Y C X be a minimal subset of X such

that

me, (Y,

d)

m + 1; then,

mC,

(Y

\ {y},

d)

::;

m for all y E

Y.

This distance space (Y,

d)

does

the

job

as

WI

.?:

m

2

in view of relation (a) above. One proceeds in the same way for

showing the inequality:

hem)

.?:

m

2

-1

for m even. Namely, one considers now

for

(X,

d)

the

graphic metric space of

K1,m-l

X

K1,m+1

with

me, (X,

d)

m + 1

and

(Y,

d)

is

a subspace such

that

mi,

(Y,

d)

= m +

1,

me,

(Y

\ {y},

d)

::;

m for

all

y E

Y.

I

To conclude let us mention

that

the exact value of the i'l-dimension

of

the

equidistant metric is not known. This amounts to determining the

maximum

number

of

equidistant points (with respect to the i'l-distance)

that

can

be placed

in

the

m-dimensional space for given m. This maximum is

at

least 2m, as the

coordinate vectors

±e; (i =

1,

...

,

m)

form obviously

an

equidistant set of 2m

points. Is

it

the best one can do ?

So

we

have

the

following problem:

Problem

11.1.7. Show that there

are

at most

2m

equidistant points in the

m-dimensional

i'l-space

(lRffi,

de,),

Bandelt, Chepoi

and

Laurent

[1997]

have settled Problem 11.1.7 in dimension

m

::;

3,

but

the problem remains open

in

dimension m

.?:

4.

In

other words,

mi,

(1m)

::;

with

equality if m

::;

8,

but

it

is

not known whether equality

holds for m.?:

11.1.2

A

Canonical

Decomposition

for

Distances

An i'l-embeddable distance d on the set

Vn

can be decomposed as a nonnegative

sum

of

cut

semimetrics.

In

general, there

is

not

unicity of such a decomposition.

Bandelt and Dress

[1992]

develop a theory

that

permits to decompose d

in

a

unique

way.

They achieve this by requiring some very specific properties for the

cuts entering the decomposition. Moreover, the theory applies to

an

arbitrary

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.