Дейт К. Введение в системы баз данных
Подождите немного. Документ загружается.


поясняется ниже.
■ ■BBBBBBB Неключевой атрибут — это атрибут, который не задействован первичным
ключом рассматриваемого отношения.
■ ■BBBBBBB Два или несколько атрибутов называются взаимно независимыми, если ни
один из них не зависит функционально от какой-либо комбинации остальных
атрибутов. Подобная независимость подразумевает, что каждый такой атрибут
может быть обновлен независимо от остальных.
Например, отношение Р (отношение товаров) находится в ЗНФ согласно
следующему определению: атрибуты PNAME (название товара), COLOR (цвет),
WEIGHT (вес) и CITY (город) независимы (т.е. у товаров можно менять цвета без
изменения их веса) и неприводимо зависимы по отношению к первичному ключу
Р#.
Такое неформальное определение ЗНФ может быть интерпретировано в
следующей более интуитивной форме.
■ ■BBBBBBB Отношение находится в третьей нормальной форме тогда и только тогда,
когда каждый кортеж состоит из значения первичного ключа, которое
идентифицирует некоторую сущность, и набора пустых значений или значений
взаимно независимых атрибутов, некоторым образом описывающих эту
сущность.
К отношению Р применимо и это определение, так как каждый кортеж
отношения Р состоит из значения первичного ключа (номер товара),
идентифицирующего некоторый товар реального мира, и четырех дополнительных
взаимно независимых значений (название товара, цвет товара, вес товара и город, в
котором находится этот товар).
Теперь можно вернуться к описанию процедуры нормализации и дать
определение 1НФ.
■ ■BBBBBBB Отношение находится в первой нормальной форме тогда и только тогда,
когда все используемые домены содержат только скалярные значения.
В этом определении всего лишь утверждается, что любое нормализованное
отношение находится в 1НФ. Однако отношение, которое находится только в 1НФ
(т.е. не находится ни во второй, ни в третьей нормальной форме) обладает
структурой, по некоторым причинам не совсем желательной. Для иллюстрации
этого факта допустим, что информация о поставщиках и поставках содержится не в
двух отношениях S и SP, а в одном:
Это расширенная версия приведенного выше отношения SCP с теми же
обычными значениями атрибутов, за исключением следующего дополнительного
ограничения:
(Атрибут STATUS функционально зависим от атрибута CITY; значение этого
ограничения состоит в том, что статус поставщика определяется его
местонахождением, например все поставщики из Лондона должны иметь статус 20.)
Кроме того, для упрощения изложения атрибут SNAME далее будет
игнорироваться. Тогда первичным ключом отношения FIRST является комбинация
{S#, Р#}, а диаграмма Ф3 будет иметь вид, показанный на рис. 10.5.

Обратите внимание, что эта диаграмма Ф3 "сложнее" диаграммы для
отношения в ЗНФ. Как было сказано выше, в диаграмме ФЗ для отношения в ЗНФ
стрелки начинаются только с первичных ключей (взгляните на рис. 10.4). Тогда как
в диаграмме ФЗ для отношения, которое не находится в ЗНФ (например, диаграмма
отношения FIRST), с первичных ключей начинаются также дополнительные
стрелки, которые и запутывают всю картину. Фактически в отношении FIRST
нарушаются оба условия, (а) и (б), из приведенного выше определения ЗНФ, т.е.
неключевые атрибуты не все взаимно независимы, поскольку атрибут STATUS
зависит от атрибута CITY (одна дополнительная стрелка), и не все неприводимо
зависимы от первичного ключа, поскольку атрибуты STATUS и CITY каждый в
отдельности зависимы от атрибута S# (еще две дополнительные стрелки).
Для иллюстрации некоторых трудностей, порождаемых этими стрелками, на
рис. 10.6 приведена таблица данных для отношения FIRST. Эти значения показаны в
обычном виде, за исключением того, что статус поставщика S3 изменен со значения
30 на значение 10, чтобы удовлетворить новому ограничению, согласно которому
значение атрибута CITY определяет значение атрибута STATUS. Таким образом,
избыточность очевидна, поскольку в каждом кортеже для поставщика S1 указано
значение London для атрибута CITY и, кроме того, в каждом кортеже для значения
London указано значение 20 для атрибута STATUS.
Избыточность в отношении FIRST приводит к разным аномалиям обновления,
получившим такое название по историческим причинам, т.е. к трудностям при
выполнении операций обновления типа INSERT (вставка), DELETE (удаление) и
UPDATE (обновление). Для начала рассмотрим избыточность типа поставщик-

город, соответствующую функциональной зависимости S#
®
CITY, и
перечисленные ниже проблемы с операциями обновления.
■ ■BBBBBBB INSERT. Нельзя вставить данные о том, что некоторый поставщик
находится в некотором городе, не указывая хотя бы один товар, поставляемый
этим поставщиком. Действительно, в таблице на рис. 10.6 не показан поставщик
S5 из Афин потому, что до тех пор, пока этот поставщик не поставляет
некоторый товар, для него не задано значение первичного ключа. (Здесь
предполагается, что на отношение FIRST наложено соответствующее
ограничение целостности, более подробно описанное в главе 5.)
■ ■BBBBBBB DELETE. Если удалить только один кортеж отношения FIRST для
некоторого поставщика, при этом будет удалена не только информация о
поставке товара некоторым поставщиком, но также и информация о том, что
этот поставщик находится в некотором городе. Например, если в отношении
FIRST удалить кортеж со значением S3 атрибута S# и значением Р2 атрибута Р#,
будет утрачена информация о том, что поставщик S3 находится в Париже.
(Образно говоря, удаление и вставка в некотором смысле обратные стороны
одной медали.)
Замечание. В действительности проблема заключается в том, что в отношении
FIRST содержится очень много совместной информации, поэтому при удалении
некоторого кортежа приходится удалять слишком много другой информации. А
точнее, отношение FIRST содержит информацию о поставках и информацию о
поставщиках. Таким образом, удаление информации о поставке вызывает также
удаление информации о поставщике. Для решения этой проблемы нужно
разделить информацию на несколько частей, т.е. разместить информацию о
поставках в одном отношении, а о поставщиках — в другом (как раз этому и
посвящен данный раздел). Таким образом, неформально процедуру
нормализации можно охарактеризовать как процедуру разбиения логически
несвязанной информации по отдельным отношениям.
■ ■BBBBBBB UPDATE. Название города для определенного поставщика повторяется в
отношении FIRST множество раз, и это приводит к возникновению проблем при
обновлении. Например, если поставщик S1 переместится из Лондона в
Амстердам, то возникает проблема, связанная либо с поиском в отношении
FIRST всех кортежей, в которых соединены S1 и Лондон (для внесения
соответствующих изменений), либо с получением несовместимого результата (в
одном кортеже городом поставщика S1 будет Лондон, а в другом — Амстердам).
Для решения этой проблемы, как уже упоминалось, нужно заменить отношение
FIRST двумя следующими:
Диаграммы ФЗ для этих двух отношений показаны на рис. 10.7, а таблицы
данных — на рис. 10.8. Обратите внимание, что теперь в них включена информация
о поставщике S5 (в отношение SECOND, но не в отношение SP), а отношение SP
теперь точно совпадает с отношением поставок.

Важно отметить, что переработанная таким образом структура позволяет
преодолеть все перечисленные ранее проблемы, связанные с операциями
обновления.
■ ■BBBBBBB INSERT. Теперь с помощью вставки соответствующего кортежа в
отношение SECOND можно включить информацию о том, что поставщик S5
находится в Афинах, даже если он в настоящий момент не поставляет никаких
товаров.
■ ■BBBBBBB DELETE. Теперь можно исключить информацию о поставке, в которой
соединены сведения о поставщике S3 и о товаре Р2, удаляя соответствующий
кортеж из отношения SP, при этом информация о том, что поставщик S3
находится в Париже, не утрачивается.
■ ■BBBBBBB UPDATE. В переработанной структуре название города для каждого
поставщика появляется всего один раз, поскольку существует только один
кортеж для данного поставщика в отношении SECOND (атрибут S# является
первичным ключом для такого отношения). Иначе говоря, избыточность данных
S#–CITY устранена. Благодаря этому теперь можно раз и навсегда изменить в
соответствующем кортеже отношения SECOND название города для поставщика
S1, например вместо Лондона задать Амстердам.
Сравнивая рис. 10.7 и 10.5, можно заметить, что суть разбиения отношения
FIRST на отношения SECOND и SP состоит в исключении зависимостей, которые не
были неприводимыми, и именно благодаря этому удается избежать упомянутых
ранее трудностей. Интуитивно можно сказать, что в отношении FIRST с помощью

атрибута CITY описывается не сущность, идентифицируемая первичным ключом
(поставка), а поставщик, выполняющий эту поставку (аналогичное утверждение
можно сделать и об атрибуте STATUS). Перемешивание двух этих типов
информации в одном и том же отношении и стало причиной возникновения
указанных ранее проблем.
Теперь пришло время определить 2НФ при условии, что существует только
один потенциальный ключ, который является первичным ключом.
■ ■BBBBBBB Отношение находится во второй нормальной форме тогда и только тогда,
когда оно находится в первой нормальной форме и каждый неключевой атрибут
неприводимо зависим от первичного ключа.
Оба отношения, SECOND и SP, находятся во второй нормальной форме с
первичными ключами S# и {S#, P#} соответственно, а отношение FIRST не
находится в ней. Всякое отношение, которое находится в 1НФ и не находится в
2НФ, всегда можно свести к эквивалентному набору отношений, находящихся в
2НФ.
Этот процесс заключается в замене отношения в 1НФ подходящим набором
проекций, эквивалентных исходному отношению в том смысле, что его можно
восстанавливать с помощью обратного соединения этих проекций. В данном
примере отношения SECOND и SP — проекции отношения FIRST, которое является
соединением отношений SECOND и SP по атрибуту S#. (За исключением того
факта, что отношение SECOND может содержать кортежи, например, такого типа,
как кортеж для поставщика S5, который не имеет аналога в отношении FIRST (см.
рис. 10.8). Иначе говоря, новая структура может даже содержать информацию,
которую невозможно представить в исходной структуре. В этом смысле новую
структуру можно рассматривать как более правдоподобное представление реального
мира.)
Таким образом, первым этапом процедуры нормализации является создание
проекций для исключения "приводимых" функциональных зависимостей.
Рассмотрим в качестве примера приведенное ниже отношение R:
Согласно порядку нормализации это отношение следует заменить двумя
проекциями,
Отношение R может быть восстановлено с помощью соединения отношений R1
и R2 по внешнему и совпадающему с ним первичному ключу этих отношений.
Однако структура отношений SECOND–SP все еще может вызвать некоторые
проблемы. Что касается отношения SP, оно вполне удовлетворительно, находится в
ЗНФ и потому останется без изменений до конца этого раздела. С другой стороны,
неключевые атрибуты в отношении SECOND не являются взаимно независимыми.

Диаграмма ФЗ для отношения SECOND все еще остается "более сложной", чем
диаграмма ФЗ для отношения в ЗНФ. В частности, зависимость атрибута STATUS
от атрибута S# хотя и является функциональной и действительно неприводимой,
она также транзитивна (через атрибут CITY), т.е. каждое значение S# определяет
значение CITY, а значение CITY, в свою очередь, определяет значение STATUS. В
общем, как уже объяснялось в главе 9, если выполняются обе зависимости А®В и
В®С, то выполняется также зависимость А®С. Таким образом, транзитивные
зависимости могут опять привести к перечисленным ниже аномалиям обновления.
(Здесь основное внимание будет сосредоточено на избыточности данных типа
город-статус, соответствующей функциональной зависимости CITY®STATUS.)
■ ■BBBBBBB INSERT. Нельзя включить данные о некотором городе, обладающем
некоторым статусом, например, нельзя указать, что все поставщики из Рима
обладают статусом 50, до тех пор пока в этом городе не существует некоторого
конкретного поставщика (здесь вновь предполагается, что задано некое правило
с ограничением целостности).
■ ■BBBBBBB DELETE. При удалении из отношения SECOND кортежа для некоторого
города будет удалена не только информация о данном поставщике, но также
информация о том, каким статусом обладал этот город. Например, при удалении
из отношения SECOND кортежа для поставщика S5 будет утрачена информация
о том, что для Афин был задан статус 30. (Здесь, образно говоря, операции
вставки и удаления являются двумя сторонами одной медали.)
Замечание. Вновь причиной этих неприятностей является совместная
информация: отношение SECOND содержит информацию о поставщиках и
вместе с ней информацию о городах. Для разрешения этой ситуации следует
поступить так, как и раньше, т.е. "разобрать" всю эту информацию и перенести в
одно отношение сведения о поставщиках, а в другое — сведения о городах.
■ ■BBBBBBB UPDATE. В отношении SECOND статус для каждого города повторяется
несколько раз (поэтому оно все еще характеризуется некоторой избыточностью).
Таким образом, при изменении значения статуса Лондона с 20 на 30 возникнет
либо проблема необходимости поиска в отношении SECOND всех кортежей для
Лондона (для внесения соответствующих изменений), либо проблема получения
несовместимого результата (в одном кортеже статус для Лондона может быть
равен 20, а в другом — 30).
Вновь для решения этой проблемы нужно заменить исходное отношение
SECOND двумя следующими проекциями:
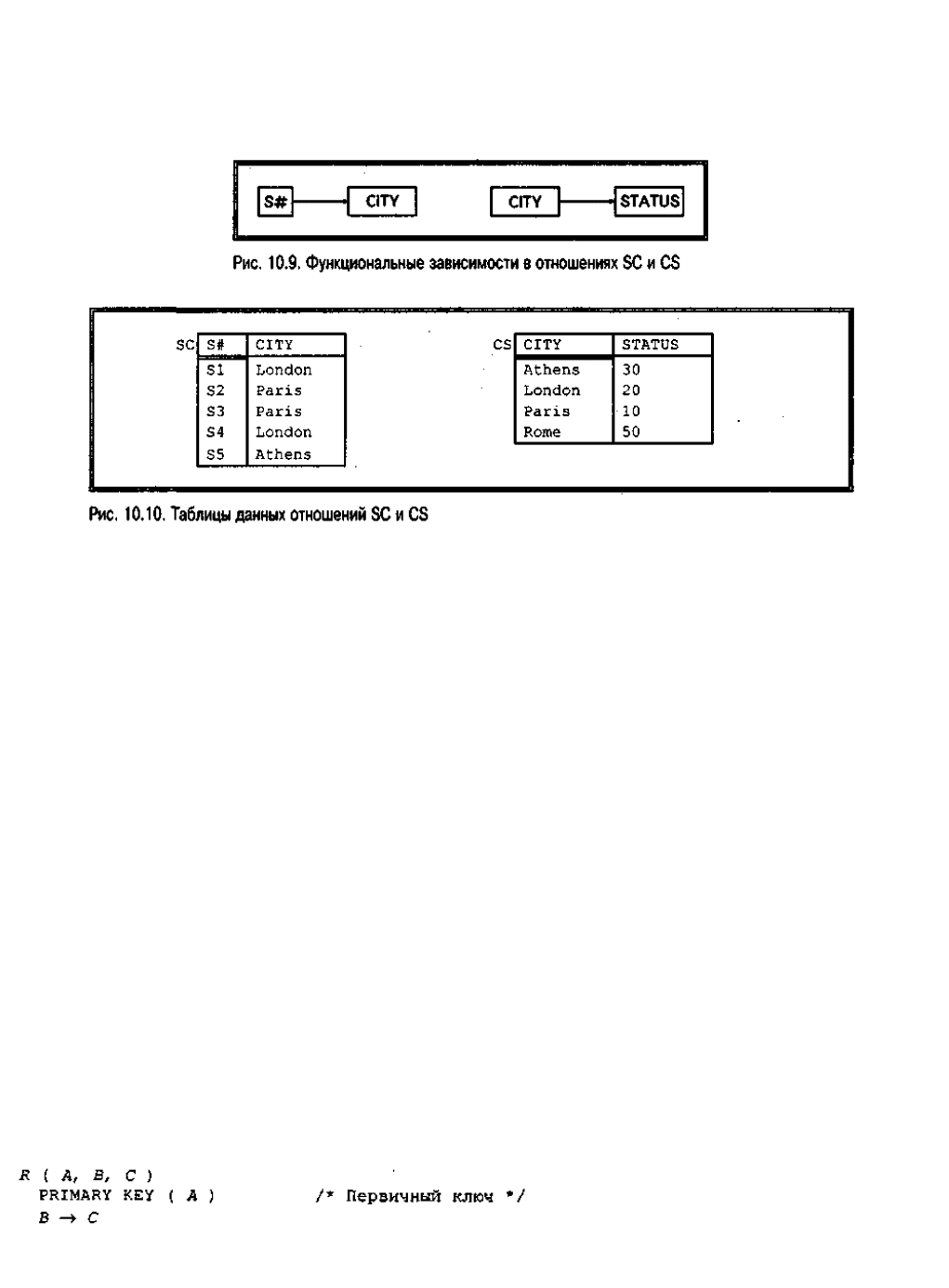
Диаграммы Ф3 для этих двух отношений показаны на рис. 10.9, а таблицы
данных — на рис. 10.10. Обратите внимание, что информация о статусе Рима
(Rome) включена только в отношение CS. Данное преобразование обратимо,
поскольку отношение SECOND является соединением отношений SC и CS по
атрибуту CITY.
Следует еще раз отметить, что переработанная структура позволяет преодолеть
все описанные проблемы с операциями обновления. Читателю предлагается
самостоятельно разобраться с подробностями решения этих проблем. Сравнивая
рис. 10.9 и 10.7, можно заметить, что благодаря дальнейшей декомпозиции удалось
исключить транзитивную зависимость атрибута STATUS от атрибута S# с
разрешением всех существовавших до этого трудностей. Интуитивно можно
утверждать, что атрибут STATUS в отношении SECOND описывает не сущность,
идентифицируемую первичным ключом (т.е. поставщика), а город поставщика.
Именно смешивание двух этих типов информации в одном отношении ранее
приводило к описанным проблемам.
Теперь можно дать определение для ЗНФ при условии, что существует только
один потенциальный ключ, который также является первичным ключом.
■ ■BBBBBBB Отношение находится в третьей нормальной форме тогда и только тогда,
когда оно находится во второй нормальной форме и каждый неключевой
атрибут нетранзитивно зависит от первичного ключа. (Под "нетранзитивной
зависимостью" подразумевается отсутствие какой-либо взаимной зависимости в
изложенном выше смысле.)
Отношения SC и CS находятся в ЗНФ, причем первичными ключами в них
являются атрибуты S# и CITY соответственно, а отношение SECOND не находится
в ЗНФ. Отношение, которое находится в 2НФ, но не находится в ЗНФ, всегда может
быть приведено к эквивалентному набору отношений в ЗНФ. Как уже говорилось
ранее, этот процесс обратим и, следовательно, никакая информация при таком
приведении не утрачивается. Однако в ЗНФ может содержаться такая информация
(например, статус Рима равен 50), которая не может быть представлена в исходном
отношении в 2НФ. (Отсюда следует, что если комбинация отношений SECOND-SP
может рассматриваться как более правдоподобное представление реального мира,
чем отношение FIRST, то и комбинация отношений SC–CS правдоподобнее
отношения SECOND, которое находится в 2НФ.)
Подводя итог, можно сказать, что вторым этапом нормализации является
создание проекций для исключения транзитивных зависимостей. Рассмотрим в
качестве примера отношение :
Согласно порядку нормализации это отношение следует заменить двумя
проекциями,
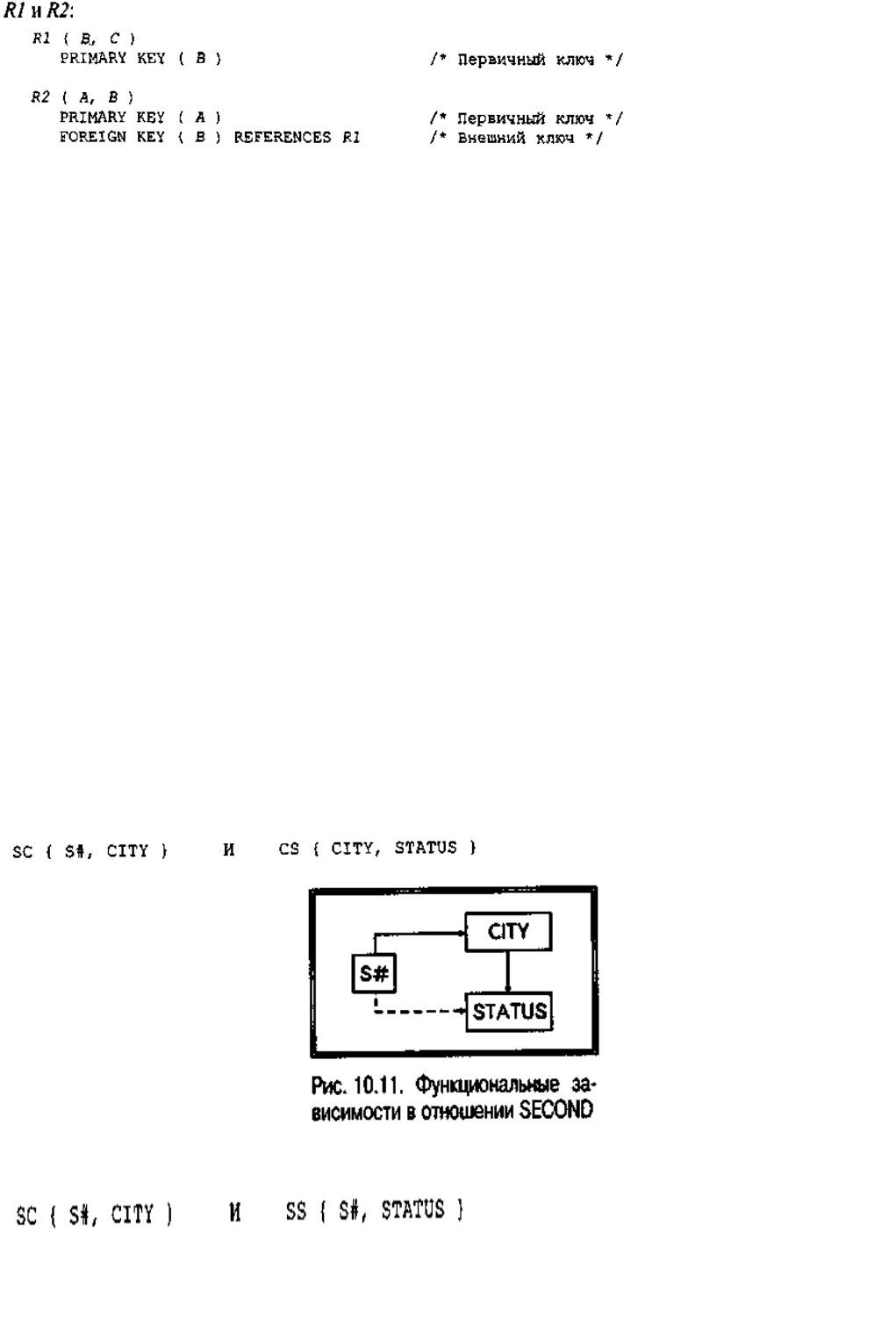
Отношение R может быть восстановлено с помощью соединения отношений R1
и R2 по внешнему и совпадающему с ним первичному ключу этих отношений.
В заключение следует подчеркнуть, что уровень нормализации данного
отношения определяется семантикой, а не конкретными значениями данных в
некоторый момент времени. Нельзя с первого взгляда на таблицу с данными для
заданного отношения определить, находится ли оно, например, в 3НФ. Для этого
также необходимо представлять себе их смысл, т.е. существующие между ними
зависимости. Следует также отметить: даже зная о зависимостях данного
отношения, нельзя доказать того, что оно находится в ЗНФ. В таком случае можно
лишь показать, что эти данные не нарушают никаких зависимостей, и, если это так,
высказать предположение о том, что эти данные не противоречат гипотезе о
принадлежности отношения к ЗНФ. Однако этот факт не гарантирует, что
предложенная гипотеза верна.
24. 10.4. Сохранение зависимости
В процессе приведения отношений часто возникают ситуации, когда данное
отношение может быть подвергнуто операции декомпозиции разными способами.
Рассмотрим снова приведенное выше отношение SECOND с функциональными
зависимостями S#®CITY, CITY®STATUS и, следовательно, транзитивной
зависимостью S#®STATUS (на рис. 10.11 транзитивная зависимость показана
пунктирной стрелкой).
Выше отмечалось, что аномалии обновления, которые сопровождают
отношение SECOND, можно преодолеть с помощью декомпозиции с заменой этого
отношения двумя проекциями в ЗНФ.
Назовем эту декомпозицию просто "декомпозицией А", имея в виду, что для нее
существует альтернативная "декомпозиция В":
При этом обе проекции SC одинаковы как для А, так и для В. Декомпозиция В
происходит также без потери информации, а обе ее проекции находятся в ЗНФ.
Однако по некоторым причинам декомпозиция В менее желательна, чем

декомпозиция А. Например, после выполнения декомпозиции В все еще невозможно
вставить информацию о том, что некоторый город имеет некоторый статус, без
указания поставщика из этого города.
Рассмотрим этот пример подробнее. Прежде всего заметим, что зависимости
проекций в декомпозиции А отмечены сплошными стрелками (см. рис. 10.11), тогда
как одна из зависимостей проекций декомпозиции В отмечена пунктирной стрелкой.
В декомпозиции А две проекции независимы друг от друга в следующем смысле:
обновления в каждой из проекций могут быть выполнены совершенно независимо
друг от друга. (Конечно, за исключением ограничения целостности для SC и CS.)
Если такое обновление допустимо только в контексте данной проекции, т.е. не
нарушается уникальность первичного ключа для этой проекции, то соединение этих
двух проекций после обновления всегда будет равносильно отношению SECOND
(т.е. при соединении не будут нарушены ограничения, наложенные на Ф3 в
отношении SECOND). В декомпозиции В, наоборот, обновление любой из двух
проекций должно тщательно фиксироваться, чтобы гарантировать отсутствие
нарушения зависимости CITY
®
STATUS (если два поставщика находятся в одном
и том же городе, они должны иметь одинаковый статус; в качестве примера
разберите случай, когда в декомпозиции В поставщик S1 переместится из Лондона в
Париж). Иначе говоря, обе проекции декомпозиции В не являются независимыми
одна от другой.
Основная проблема заключается в том, что в декомпозиции В функциональная
зависимость CITY®STATUS становится ограничением между отношениями.
(Следует отметить, что во многих современных программных продуктах это
ограничение должно поддерживаться с помощью процедурной обработки.) В
декомпозиции А, наоборот, транзитивная зависимость S#®STATUS является
ограничением между отношениями, которое автоматически выполняется при
задействовании двух ограничений внутри отношений: S#®STATUS и
CITY®STATUS. Привести в действие эти ограничения достаточно просто за счет
соответствующих ограничений, наложенных на уникальность первичных ключей.
Концепция независимых проекций, таким образом, обеспечивает критерий
выбора одной из нескольких возможных декомпозиций. Декомпозиция с
независимыми проекциями в приведенном выше общем смысле предпочтительнее
той, в которой проекции зависимы. Риссанен (Rissanen) [10.6] показал, что проекции
R1 и R2 отношения R независимы в упомянутом выше смысле тогда и только тогда,
когда
■ ■BBBBBBB каждая ФЗ в отношении R является логическим следствием функциональных
зависимостей в проекциях R1 и R2;
■ ■BBBBBBB общие атрибуты проекций R1 и R2 образуют потенциальный ключ, по
крайней мере, для одной из них.
Рассмотрим заданные выше декомпозиции А и В. В декомпозиции А две
проекции независимы, поскольку их общий атрибут CITY является первичным
ключом для отношения CS и каждая ФЗ отношения SECOND либо находится в
одной из проекций, либо является логическим следствием имеющихся. В
декомпозиции В, наоборот, две проекции не являются независимыми, поскольку
зависимость CITY —»STATUS не может быть выведена из ФЗ этих проекций, хотя
их общий атрибут S# является потенциальным ключом для обеих проекций.

(Следует отметить, что третий вариант декомпозиции с заменой отношения
SECOND проекциями {S#, STATUS} и {CITY, STATUS} не является допустимой
декомпозицией, поскольку выполняется с потерей информации. Упражнение.
Докажите это утверждение.)
Терминология. Отношение, которое не может быть подвергнуто декомпозиции с
получением независимых проекций, называется атомарным [10.6]. Однако это не
значит, что любое неатомарное отношение может быть разбито на атомарные
компоненты. Например, отношения S и Р из рассматриваемой ранее базы данных
поставщиков и товаров (поставщиков и деталей) не являются атомарными, но
дальнейшая их декомпозиция была бы бессмысленной. Отношение SP, наоборот,
является атомарным.
Идея нормализации с декомпозицией на независимые проекции (в смысле
Риссанена) называется декомпозицией с сохранением зависимости. В заключение
следует привести несколько более строгих замечаний по поводу этой идеи.
1. 1.BBBBBB Пусть дано некоторое отношение R, которое после выполнения всех этапов
процедуры нормализации заменяется множеством отношений R1, R2,... Rn
(конечно, все они являются проекциями отношения R).
2. 2.BBBBBB Пусть также задано множество зависимостей S для исходного отношения R,
и множества зависимостей S1, S2,... Sn для отношений R1, R2,... Rn.
3. 3.BBBBBB Каждая ФЗ множества Si будет относиться только к атрибутам множества Ri
(i =1, 2, 3,...,). Таким образом, приведение в действие ограничений (ФЗ) в любом
заданном множестве Si представляется достаточно простой задачей. Однако в
данном случае необходимо задействовать ограничения из исходного множества
S. При этом следовало бы выбрать такую декомпозицию на отношения R1, R2, ...
Rn, для которой совместное приведение в действие отдельных множеств
ограничений S1, S2, ... Sn эквивалентно приведению в действие ограничений в
исходном множестве S. Иначе говоря, декомпозиция должна выполняться с
сохранением зависимостей.
4. 4.BBBBBB Пусть S' является объединением множеств зависимостей S1, S2, ... Sn.
Обратите внимание, что в общем случае равенство S'=S не выполняется, однако
для выполнения декомпозиции с сохранением зависимостей достаточно, чтобы
замыкания S и S' были равны друг другу (понятие замыкания множества ФЗ
рассматривалось в главе 9).
5. 5.BBBBBB В общем случае не существует эффективного способа вычисления
замыкания S
+
множества Ф3, поэтому вычисление и сравнение двух замыканий
трудноосуществимо. Тем не менее, существует эффективный метод проверки,
будет ли данная декомпозиция выполняться с сохранением зависимости.
Описание подробностей этого алгоритма выходит за рамки данной книги, однако
они описываются в книге Ульмана (Ullman) [7.16].
Замечание. В ответах на упражнения в конце этой главы описан алгоритм
выполнения декомпозиции без потерь и с сохранением зависимости для
произвольного отношения с разбиением на множество проекций в ЗНФ.
25. 10.5. Нормальная форма Бойса-Кодда
В этом разделе опускается упрощающее допущение о том, что каждое
отношение имеет только один потенциальный ключ (а именно первичный ключ), и
