Дейт К. Введение в системы баз данных
Подождите немного. Документ загружается.


без изменения замыкания (т.е. без утраты некоторой информации). И наоборот,
приведенные ниже множества ФЗ не являются неприводимыми.
Теперь можно сделать утверждение, что для каждого множества ФЗ существует,
по крайней мере, одно эквивалентное множество, которое является неприводимым.
Это достаточно легко продемонстрировать на следующем примере. Пусть дано
исходное множество зависимостей S, тогда благодаря правилу декомпозиции можно
без утраты общности предположить, что каждая ФЗ в множестве S имеет
одноэлементную правую часть. Далее для каждой зависимости f этого множества S
следует проверить каждый атрибут А в левой части f. Если множество S и
множество зависимостей, полученное с помощью устранения атрибута А в левой
части f эквивалентны, то этот атрибут следует удалить. Затем для каждой
оставшейся в множестве S зависимости f, если S и S – f эквивалентны, следует
удалить f из множества S. Получившееся в результате таких действий множество S
является неприводимым и эквивалентно исходному множеству S.
Пример. Пусть дано отношение R с атрибутами В, С, D и следующими ФЗ:
Теперь попробуем найти неприводимое множество ФЗ, эквивалентное данному
множеству.
1. 1.BBBBBB Прежде всего следует переписать ФЗ таким образом, чтобы каждая из них
имела одноэлементную правую часть:
Нетрудно заметить, что зависимость А®В записана дважды, так что одну из них
можно удалить.
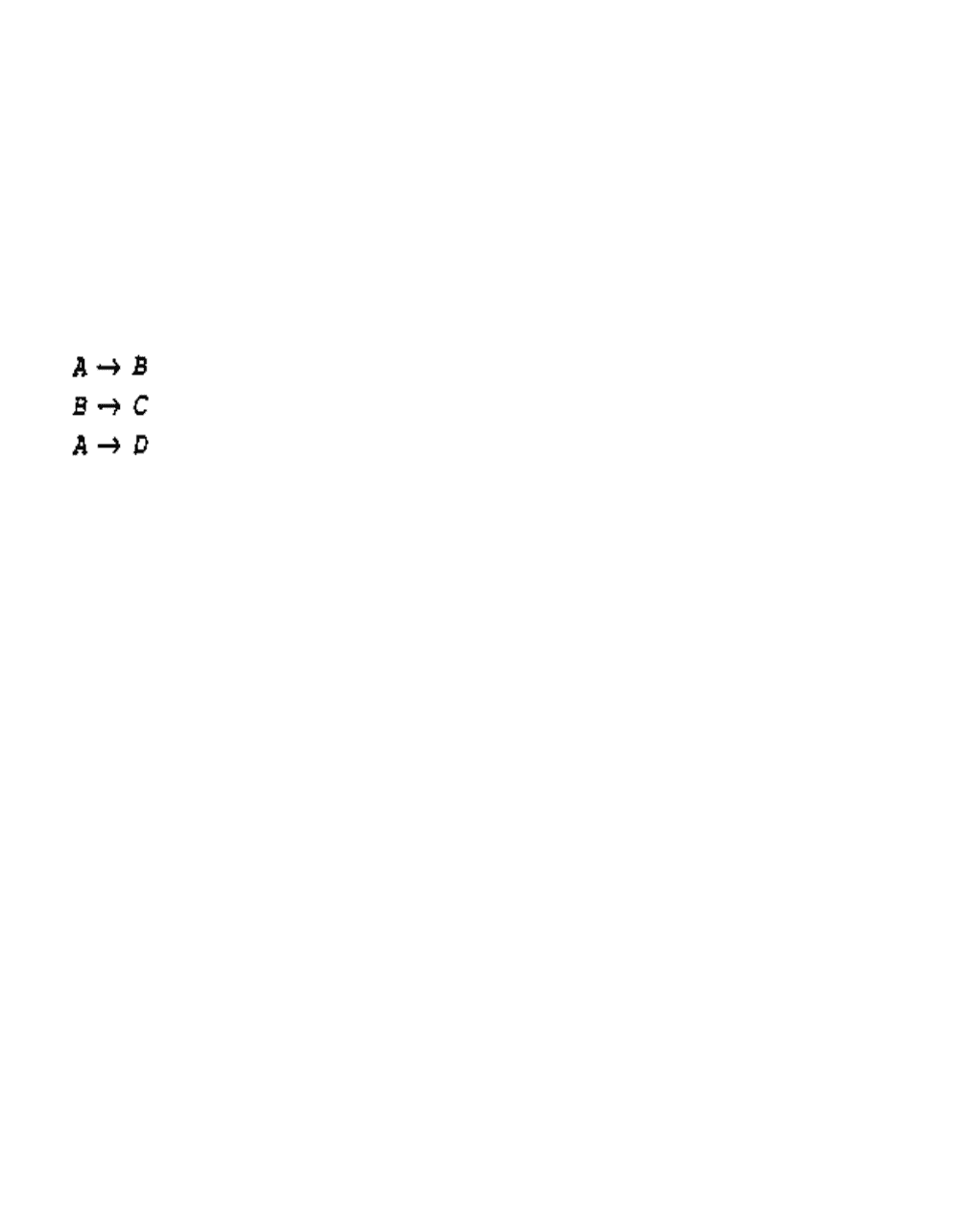
2. 2.BBBBBB Затем атрибут С может быть опущен в левой части зависимости АС®D,
поскольку дана зависимость А®С и с помощью дополнения можно получить
А®АС, а также поскольку дана зависимость АС®D и с помощью транзитивности
можно получить А®D; таким образом, атрибут С в левой части зависимости
АС®D является более точным.
3. 3.BBBBBB Далее можно заметить, что зависимость АВ®С может быть исключена,
поскольку дана зависимость А®С и с помощью дополнения можно получить
АВ®СВ, а с помощью декомпозиции — АВ®С.
4. 4.BBBBBB Наконец, зависимость А®С подразумевается зависимостями А®В и В®С, так
что она также может быть устранена. В результате получится неприводимое
множество зависимостей:
Множество зависимостей I, которое неприводимо и эквивалентно некоторому
другому множеству зависимостей S, называется неприводимым покрытием
множества S. Таким образом, с тем же успехом в системе вместо исходного
множества зависимостей S может быть использовано его неприводимое покрытие I.
Однако следует отметить, что для заданного множества ФЗ не всегда существует
уникальное неприводимое покрытие (это упоминается ниже в упражнениях).
Дальнейшая нормализация: 1НФ, 2НФ, ЗНФ, НФБК (стр. 288-310)
Глава 10
Дальнейшая
нормализация:
1НФ, 2НФ, ЗНФ, НФБК
21. 10.1. Введение
До сих пор в этой книге в качестве примера рассматривалась
база данных поставщиков и деталей с приведенной ниже
логической структурой.

В принципе, каждая деталь является товаром, который поставляет
определенный поставщик. Поэтому далее о поставке деталей мы будем говорить как
о поставке определенных товаров, т.е. база данных поставщиков и деталей может
служить базой данных поставщиков и товаров, которые они поставляют.
Теперь структура такой базы данных становится понятнее. В ней, очевидно,
должны содержаться три отношения — S, Р и SP, для которых заданы некоторые
атрибуты, например: для товара — атрибут COLOR (цвет) в отношении Р, для
города поставщика — CITY (город) в отношении S, для количества товаров — QTY
(количество) в отношении SP и т.д. Но откуда это известно? Некоторый намек на
ответ можно получить, изменяя определенным образом макет базы данных.
Предположим, например, что атрибут CITY удален из отношения поставщиков S и
добавлен к отношению поставок SP (хотя интуитивно это действие можно
охарактеризовать как ошибочное, так как понятие "город поставщика" очевидным
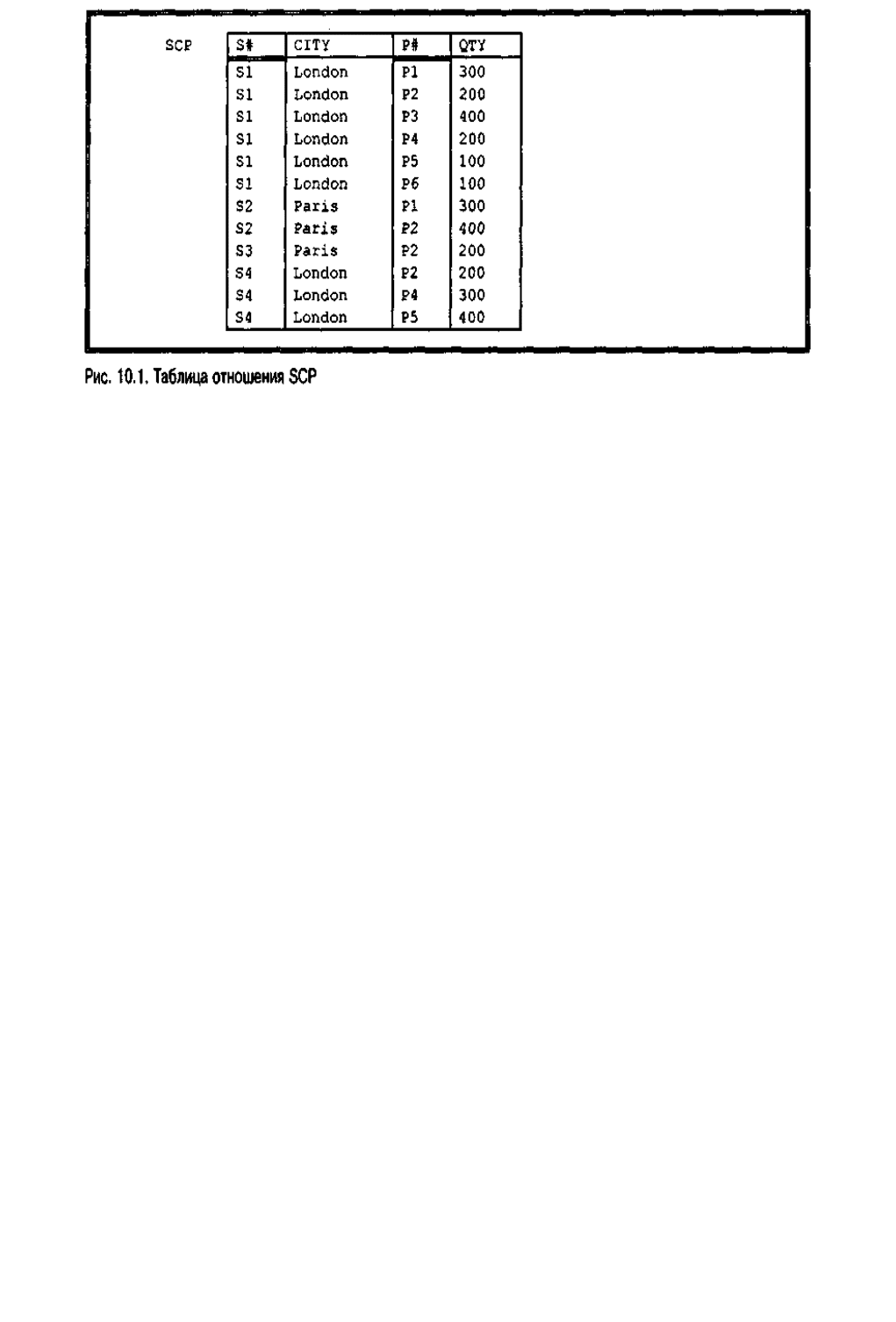
образом связано с поставщиками, а не с поставками). На рис. 10.1 показана таблица
с образцами записей для такого измененного отношения поставок. (Чтобы избежать
путаницы с обычным исходным отношением SP, измененное отношение будет далее
обозначаться SCP, как и в главе 9.)
В приведенной таблице легко заметить один из недостатков такой организации,
а именно ее избыточность. Конкретнее, в каждом кортеже отношения SCP для
поставщика S1 содержится информация о том, что поставщик S1 находится в
Лондоне; в каждом кортеже отношения SCP для поставщика S2 содержится
информация о том, что поставщик S2 находится в Париже, и т.д. В общем
информация о городе данного поставщика повторяется столько раз, сколько
поставок имеет данный поставщик. Эта избыточность, в свою очередь, приводит к
некоторым другим проблемам. Например, после обновления данных
местонахождением поставщика S1 в одном из кортежей может быть указан Лондон,
а в другом — Амстердам. Таким образом, для создания хорошего макета следует
придерживаться принципа "по одному факту в одном месте" (т.е. избегать
избыточности). Предметом дальнейшей нормализации будет всего лишь
формализация подобных простых идей, однако это должна быть формализация,
действительно имеющая большой практический смысл при проектировании базы
данных.
Конечно, отношения в реляционной базе данных всегда нормализованы в том
смысле, что содержат только "скалярные" значения. (Определение понятия
"скалярный" в этом смысле будет дано в последующих главах книги.) На рис. 4.5 в
главе 4 показан пример приведения ненормализованного отношения к
эквивалентной нормализованной форме. Однако некоторое отношение может быть
нормализовано в этом смысле и все еще обладать некоторыми нежелательными
свойствами, например отношение SCP, показанное на рис. 10.1. Принципы
дальнейшей нормализации позволяют распознать подобные случаи и свести такие
отношения к более приемлемой форме. В примере с отношением SCP эти принципы
позволили бы найти недостатки отношения и указать на необходимость его
разбиения на два "более приемлемых" отношения: одно с атрибутами {S#, CITY}, а
другое с атрибутами {S#, P#, QTY}.
Нормальные формы
Процесс дальнейшей нормализации, который далее будет упоминаться просто как
нормализация, основывается на концепции нормальных форм. Говорят, что
отношение находится в некоторой нормальной форме, если удовлетворяет
заданному набору условий. Например, отношение находится в первой нормальной
форме, или сокращенно в 1НФ, тогда и только тогда, когда оно содержит только
скалярные значения.
Замечание. Отсюда следует, что каждое нормализованное отношение
находится в первой нормальной форме. Иначе говоря, термины "нормализованное"
и "1НФ" означают одно и то же. Однако следует отметить, что термин
"нормализованное" часто используется для обозначения нормальной формы более
высокого уровня (особенно для третьей нормальной формы, 3НФ). Хотя такое
обозначение не очень корректно, оно довольно широко распространено.
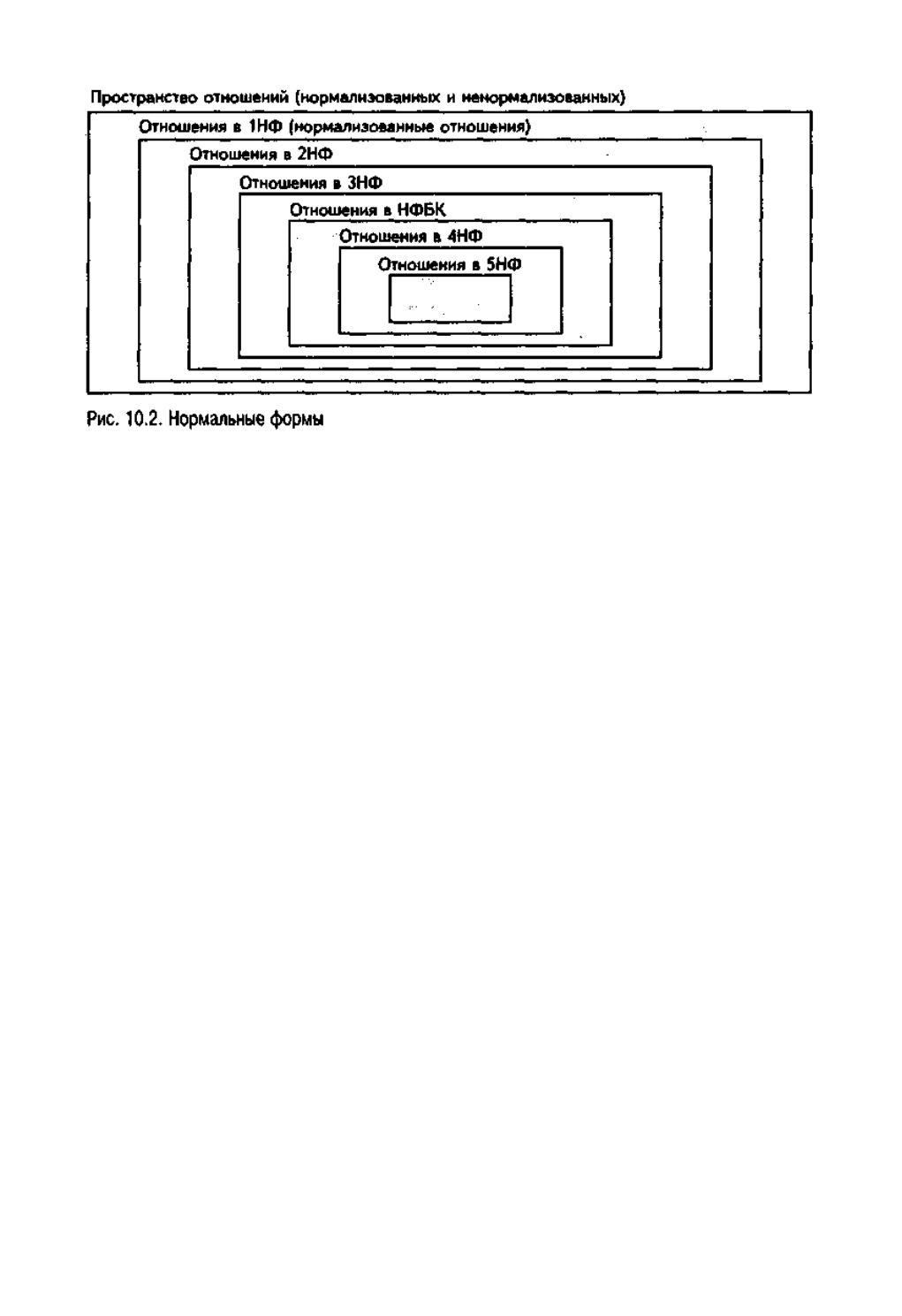
На рис. 10.2 показано несколько нормальных форм, которые определены к
настоящему времени. Первые три (1НФ, 2НФ, 3НФ) были определены Коддом
(Codd) [9.4]. Как показано на рис. 10.2, все нормализованные отношения находятся в
1НФ, некоторые отношения 1НФ находятся также в 2НФ и некоторые отношения
2НФ находятся также в 3НФ. Мотивом для введения дополнительных определений
было то, что вторая нормальная форма "более желательна" (в смысле, который будет
разъяснен позже), чем первая, а третья, в свою очередь, "более желательна", чем
вторая. Таким образом, при проектировании базы данных вообще следует
использовать отношения не только в первой или во второй, но также и в третьей
форме.
В [9.4] также приводится описание процедуры нормализации, с помощью
которой отношение заданной формы, например 2НФ, может быть преобразовано в
множество отношений в другой, более желательной, нормальной форме, например
ЗНФ. (В исходном варианте эта процедура определена только до третьей формы, но,
как будет показано дальше в этой главе, она может быть последовательно
расширена до пятой формы.) Такую процедуру можно охарактеризовать как
последовательное приведение данного набора отношений к некоторой более
желательной форме. Эта процедура обратима, т.е. всегда можно использовать ее
результат (например, множество отношений, находящихся в 3НФ) для обратного
преобразования (в исходное отношение, находящееся в 2НФ). Возможность
выполнения обратного преобразования является весьма важной характеристикой,
поскольку означает, что в процессе нормализации информация не утрачивается.
Как будет показано ниже в этой главе, оригинальное определение Кодда для
ЗНФ [9.4] приводит к некоторой неадекватности. Переработанное и более точное
понятие, данное Бойсом (Воусе) и Коддом в [10.2], является более строгим в том
смысле, что любое отношение в ЗНФ по новому определению является таковым и
по старому определению, но не всякое отношение в 3НФ по старому определению
может являться таковым по новому определению. Для того чтобы эти определения
можно было различать, отношение в ЗНФ по новому определению обычно называют
нормальной формой Бойса-Кодда — НФБК.
Впоследствии Фейгином (Fagin) в [11.8] была определена новая, четвертая
нормальная форма (4НФ), которая стала четвертой по счету, поскольку в момент ее
создания нормальная форма Бойса-Кодда считалась третьей. Совсем недавно
Фейгин в [11.9] дал определение еще одной нормальной формы, которую он назвал
проективно-соединителъной нормальной формой; она также называется пятой
нормальной формой, или ЗНФ. Как показано на рис. 10.2, некоторые отношения в
НФБК также находятся в 4НФ, а некоторые отношения в 4НФ также находятся в
5НФ.
Возникает вопрос, нельзя ли продлить эту операцию дальше для получения
шестой нормальной формы, седьмой и так до бесконечности. К ответу на этот
вопрос мы вернемся в главе 11, а пока следует заметить, что действительно

существуют дополнительные нормальные формы, которые не показаны на рис. 10.2.
Здесь же 5НФ в некотором (и очень важном) смысле рассматривается как
"окончательная" нормальная форма.
Структура главы
Целью этой главы является описание концепции дальнейшей нормализации до
уровня нормальной формы Бойса-Кодда включительно, а оставшиеся две формы
будут рассмотрены в главе 11. В целом изложение ведется согласно следующему
плану. После несколько затянувшегося введения описывается базовая концепция
декомпозиции без потерь и демонстрируется значение функциональной зависимости
(ФЗ) для формулировки этой концепции (действительно, ФЗ образует основу трех
нормальных форм Кодда и нормальной формы Бойса-Кодда). Затем представлены
три начальные нормальные формы, а на основе примера некоторого отношения
показано, как выполняется процесс нормализации вплоть до достижения ЗНФ.
После этого делается небольшое отступление с описанием альтернативных
декомпозиций, т.е. выбора "наилучшей декомпозиции" для данного отношения,
если, конечно, такой выбор возможен. Далее описывается НФБК, и в конце
приводится резюме и несколько заключительных замечаний.
Важно отметить, что далее изложение ведется с меньшей строгостью и в
рассуждениях автор в основном полагается на интуицию. Подобный подход может
быть оправдан тем, что такие понятия, как декомпозиция без потерь, нормальная
форма Бойса-Кодда и другие, несмотря на их таинственные и загадочные названия,
весьма просты и общедоступны. Во многих работах, на которые имеются ссылки,
этот материал излагается в более строгой форме.
Кроме того, следует сделать еще два вводных замечания.
1. 1.BBBBBB Как уже отмечалось, общая идея нормализации заключается в том, чтобы
при проектировании базы данных предполагалось использование отношений в
"окончательной" нормальной форме (т.е. в пятой). Однако эту рекомендацию не
следует толковать как обязательное правило, поскольку возможны ситуации,
когда принципами нормализации необходимо пренебречь (об этом упоминается
в упражнениях в конце главы). Однако очень важно, чтобы отношения
находились, по крайней мере, в первой нормальной форме. Действительно, здесь
следует подчеркнуть, что проектирование базы данных может представлять
собой чрезвычайно сложную задачу (по крайне мере, в "достаточно большой
базе данных", поскольку макеты "малых" баз данных обычно очень просты).
Нормализация значительно упрощает этот процесс, но не является панацеей.
Хотя составителю макета базы данных рекомендуется знать основные принципы
нормализации, это не значит, что макет обязательно должен быть создан на
основе одних только принципов нормализации. В главе 12 обсуждается
несколько аспектов проектирования базы данных, которые имеют весьма
отдаленное отношение или совсем не имеют отношения к нормализации как
таковой.
2. 2.BBBBBB Как упоминалось выше, процедура нормализации будет использована в
качестве основы при описании различных нормальных форм. Однако это не
значит, что на практике создание макета базы данных будет выполняться с
помощью этой процедуры. На самом деле, скорее всего, для этого будет
использована описанная в главе 12 схема типа "сверху вниз". Затем идеи
нормализации можно использовать для проверки того, чтобы полученный в
результате макет непроизвольно не нарушал никаких принципов нормализации.
Тем не менее, процедура нормализации является удобным способом
представления этих принципов. Для упрощения изложения в данной главе будет
сделано полезное допущение о том, что проектирование выполняется с помощью
процедуры нормализации.
22. 10.2. Декомпозиция без потерь и функциональные зависимости
Прежде чем приступить к рассмотрению подробностей процедуры нормализации,
следует обсудить один существенный аспект этой процедуры, а именно концепцию
декомпозиции без потерь. Как уже упоминалось, процедура нормализации включает
разбиение, или декомпозицию данного отношения на другие отношения, причем
декомпозиция должна быть обратимой, т.е. выполняться без потерь информации.
Иначе говоря, интерес представляют только те операции, которые выполняются без
потерь информации. Вопрос о том, происходит ли утрата информации при
декомпозиции, тесно связан с концепцией функциональной зависимости.
В качестве примера рассмотрим уже знакомое отношение поставщиков S с
атрибутами {S#, STATUS, CITY} (для упрощения задачи атрибут SNAME в данном
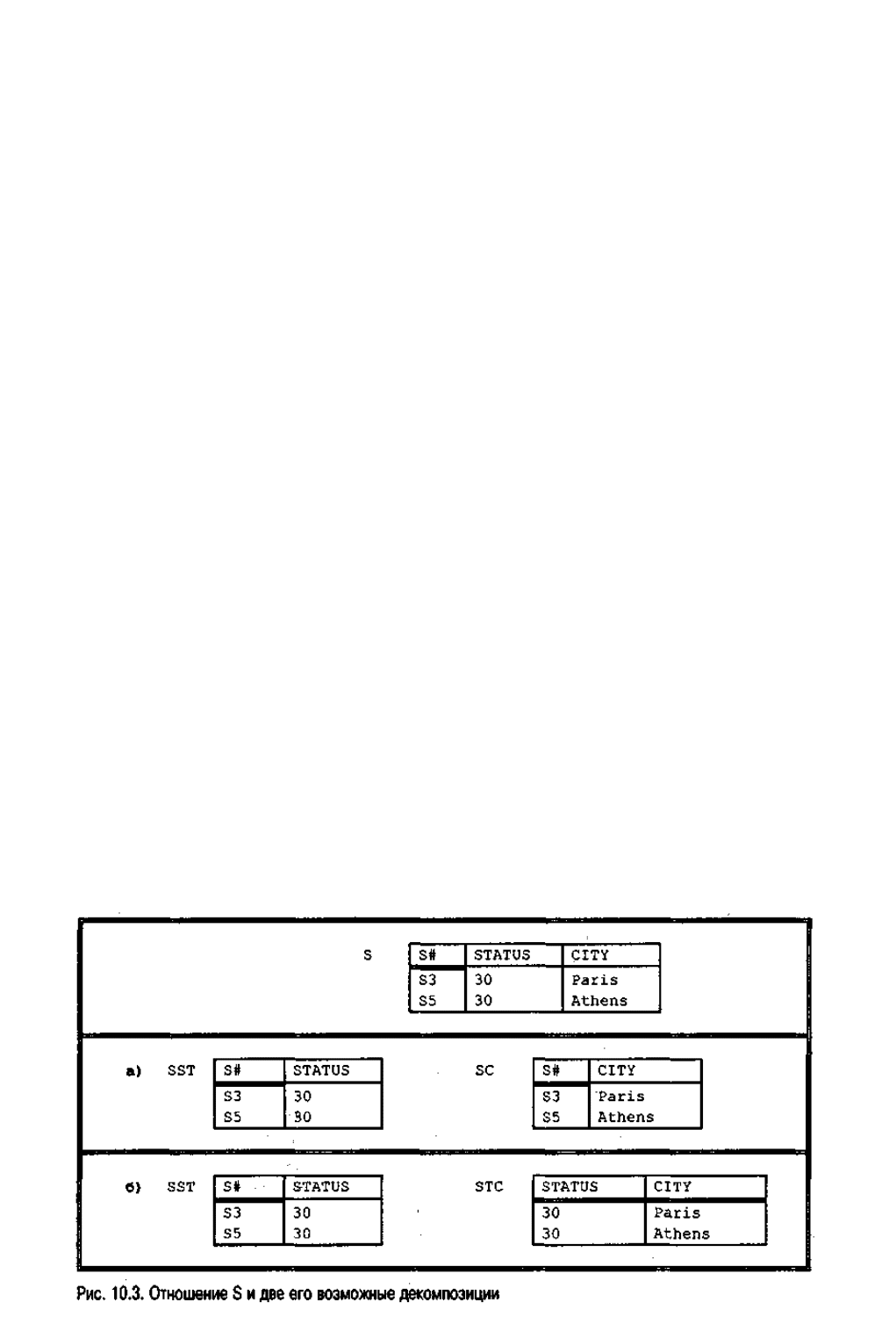
случае игнорируется). На рис. 10.3 показан пример записей этого отношения
(некоторое подмножество, приводимых ранее значений этого примера) с указанием
двух его возможных декомпозиций: (а) и (б).
Внимательно ознакомившись с этими декомпозициями, можно заметить две
особенности.
1. 1.BBBBBB В случае (а) информация не утрачивается, поскольку отношения SST и SC
все еще содержат данные о том, что поставщик S3 имеет статус 30 и находится в
Париже (Paris), а поставщик S5 имеет статус 30 и находится в Афинах (Athens).
Иначе говоря, первая декомпозиция действительно является декомпозицией без
потерь.
2. 2.BBBBBB В случае (б), наоборот, некоторая информация утрачивается, поскольку оба
поставщика имеют статус 30, но при этом нельзя сказать, какой из них в каком
городе находится. Иначе говоря, вторая декомпозиция не является
декомпозицией без потерь.

Почему получилось так, что одна декомпозиция происходит без потерь, а
другая — с потерей информации? Прежде всего, следует отметить, что процесс,
который до сих пор назывался "декомпозицией", на самом деле является
проектированием, т.е. каждое из показанных на рис. 10.3 отношений— SST, SC и
STC— в действительности является проекцией исходного отношения S. Таким
образом, оператор декомпозиции в процедуре нормализации фактически является
оператором проектирования.
Обратите внимание, что в случае (а) сохранение информации в полном объеме
означает, что при обратном соединении отношений SST и SC будет получено
исходное отношение S. В случае (б), наоборот, при обратном соединении
отношений SST и SC не будет получено исходное отношение S, а это значит, что
некоторая информация будет утрачена. (Точнее, в исходном отношении S вместе со
всеми кортежами будут содержаться "ложные" кортежи. Поскольку не существует
общего метода для различения ложных и подлинных кортежей, информация в этом
случае будет утеряна.) Иначе говоря, "обратимость" означает, что исходное
отношение равно соединению его проекций. Если оператором декомпозиции в
процедуре нормализации является операция проектирования, то обратной операцией
должна быть операция соединения (конечно, в смысле естественного соединения по
атрибутам с общими именами).
Исходя из сказанного выше, можно задать следующий вопрос. Пусть R1 и R2 —
проекции некоторого отношения R, содержащие все атрибуты отношения R. Какие
условия должны быть соблюдены для того, чтобы при обратном соединении R1 и R2
гарантировать получение исходного отношения R? Именно для ответа на этот
вопрос и возникает необходимость использования функциональных зависимостей. В
рассматриваемом примере отношение S удовлетворяет представленному ниже
неприводимому множеству Ф3. (Далее в этой главе будет считаться, что Ф3
независимы от времени, т.е. выполняются для всех допустимых значений
соответствующего отношения. Подробнее неприводимые множества Ф3 описаны в
главе 9.)
При условии, что данное отношение удовлетворяет приведенным ФЗ, можно
предположить, что отношение S равно соединению его проекций {S#, STATUS} и
{S#, CITY}. И это действительно так, что подтверждается теоремой Хеза (Heath)
[10.4].
■ ■BBBBBBB Теорема Хеза. Пусть R{A, В, С} является отношением, где А, В и С —
атрибуты этого отношения. Если R удовлетворяет зависимости A®В, то R равно
соединению его проекций {А, В} и {А, С}.
Если обозначить А как S#, В как STATUS, С как CITY, то эта теорема
утверждает, как уже отмечалось выше, что отношение S может быть разбито с
помощью операции декомпозиции на проекции {S#, STATUS} и {S#, CITY} без
утраты информации.
В то же время уже известно, что отношение S не может быть разбито без
потери информации на проекции {S#, STATUS} и {STATUS, CITY}. Теорема Хеза
не дает объяснения, почему так происходит. (Дело в том, что она формулируется как
"если..., то...", а не "тогда и только тогда, когда...". Об этом также идет речь в
упражнениях в конце главы. Более строгая формулировка теоремы Хеза будет
представлена в главе 11.) Однако интуитивно можно предположить, что при такой
декомпозиции утрачивается одна из функциональных зависимостей, т.е.
зависимость S# ® STATUS еще будет присутствовать (благодаря проекции {S#,
STATUS}), а зависимость S# ® CITY будет утрачена.
Еще о функциональных зависимостях
В завершение перечислим некоторые дополнительные замечания,
касающиеся Ф3.
1. 1.BBBBBB Неприводимые слева ФЗ. Согласно главе 9 функциональная зависимость
называется неприводимой слева, если ее левая часть "не очень велика".
Рассмотрим, например, отношение SCP, приведенное выше в этой главе, которое
удовлетворяет следующей ФЗ:
Однако атрибут Р# в левой части является избыточным для этой Ф3, и она
может быть переписана:
(Атрибут CITY функционально зависит от S#.) Эта последняя Ф3 является
неприводимой слева. Таким образом, можно сказать, что атрибут CITY
неприводимо зависим от S#, но не неприводимо зависим от {S#, P#}. (Здесь
термины "неприводимо зависим" и "неприводимая слева ФЗ" используются
вместо терминов "полная ФЗ" и "полностью зависимая", которые часто можно
встретить в литературе и прежних изданиях этой книги. Хотя последние
термины отличаются краткостью, они менее информативны и потому не очень
удобны.)
Неприводимые слева ФЗ и неприводимые зависимости играют важную роль
для определения второй и третьей нормальной формы (подробнее это обсуждается в
разделе 10.3).
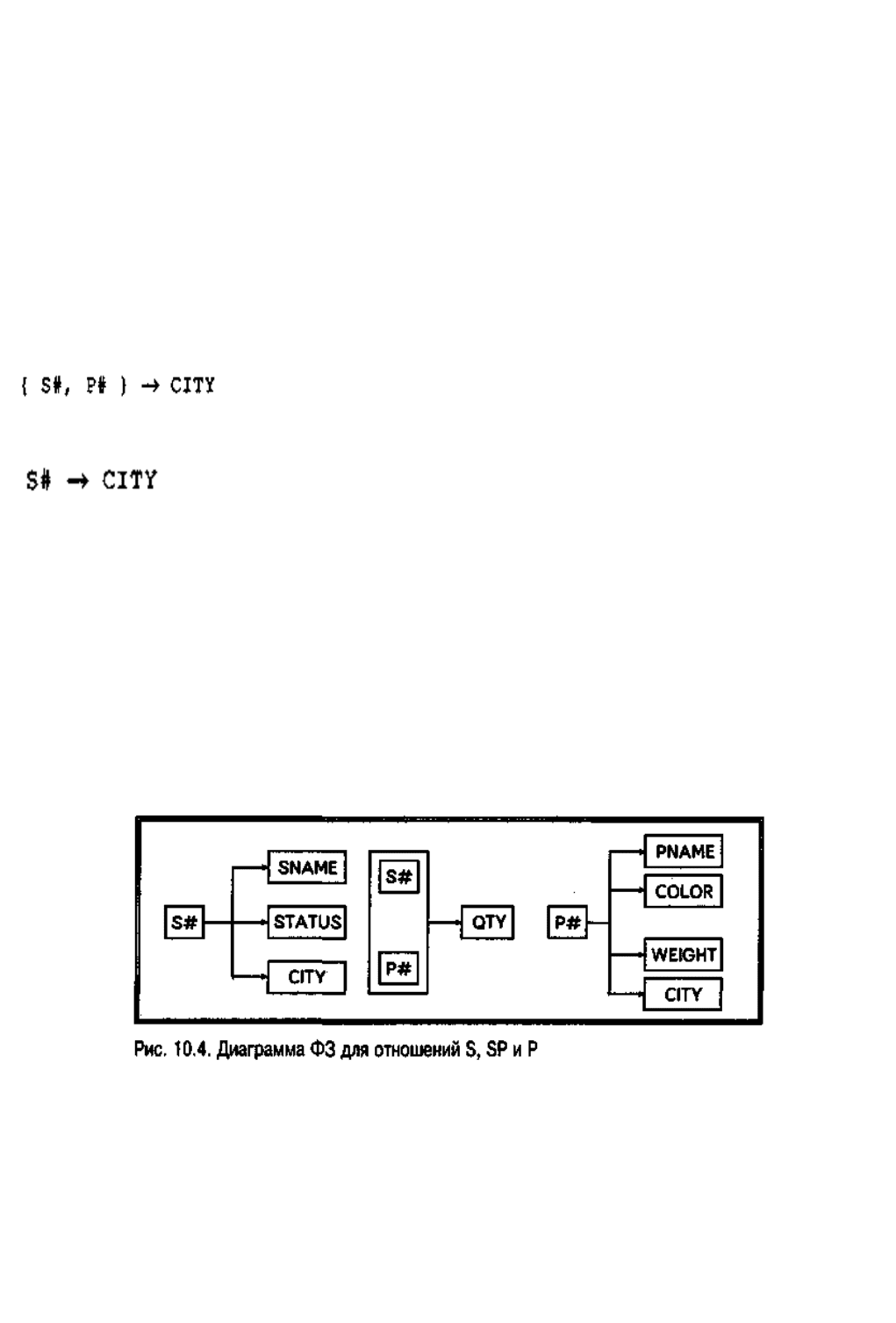
2. 2.BBBBBB Диаграммы ФЗ (также называются схемами ФЗ). Пусть дано отношение R и
некоторое неприводимое множество зависимостей I для этого отношения,
которое можно представить в виде диаграммы функциональных зависимостей
(диаграммы ФЗ). На рис. 10.4 показаны достаточно понятные по построению
диаграммы ФЗ для отношений S, SP и Р соответственно. Такие диаграммы будут
часто использоваться далее в этой главе.
Как видно из рис. 10.4, каждая стрелка начинается с потенциального ключа (на
самом деле с первичного ключа) соответствующего отношения. По определению
стрелки должны начинаться с каждого потенциального ключа, поскольку одному

значению такого ключа всегда соответствует, по крайней мере, еще одно какое-
то значение. Некоторые стрелки следовало бы исключить ввиду того, что они
вызывают определенные трудности, но стрелки, начинающиеся с
потенциальных ключей, никогда не могут быть исключены. Таким образом,
процедуру нормализации можно было бы неформально охарактеризовать как
процедуру исключения стрелок, которые не начинаются с потенциальных
ключей.
3. 3.BBBBBB ФЗ как семантическое понятие. Конечно, ФЗ — это особый вид
ограничений целостности, а потому это, несомненно, семантическое понятие.
Распознавание ФЗ является частью процесса выяснения смысла тех или иных
данных, ведь если отношение S удовлетворяет зависимости S#®CITY, это
значит, что каждый поставщик находится точно в одном городе. Иначе эту
ситуацию можно охарактеризовать следующим образом.
▪ ▪BBBBBBBBBBB В реальном мире существует некоторое ограничение, представленное в
этой базе данных, а именно: каждый поставщик находится точно в одном
городе.
▪ ▪BBBBBBBBBBB Поскольку это ограничение является частью семантики, оно должно
быть каким-то образом представлено в базе данных.
▪ ▪BBBBBBBBBBB Для этого ограничение следует задать в определении базы данных таким
образом, чтобы оно могло быть приведено в действие в СУБД.
▪ ▪BBBBBBBBBBB Способом задания ограничения в определении базы данных является
объявление ФЗ. Как будет показано ниже, концепции нормализации
приводят к весьма простым способам объявления ФЗ.
23. 10.3. Первая, вторая и третья нормальные формы
Прежде чем перейти к подробному описанию трех оригинальных нормальных
форм Кодда, следует дать предварительное и весьма неформальное определение
третьей нормальной формы для того, чтобы в общих чертах обрисовать основную
цель этого изложения. Итак, здесь будет рассмотрен процесс приведения
произвольного отношения к эквивалентному набору отношений в ЗНФ и попутно
даны более точные определения трех нормальных форм. Однако в качестве
отступления следует отметить, что формы 1НФ, 2НФ и ЗНФ имеют значение не
сами по себе, а лишь как промежуточные этапы на пути построения формы НФБК (и
форм более высокого уровня).
Предостережение. В этом разделе для простоты изложения предполагается,
что каждое отношение имеет в точности один потенциальный ключ, который
является первичным ключом. Это допущение подтверждают предлагаемые здесь
доказательства, которые (как уже отмечалось ранее) являются не очень
строгими. Далее в этой главе будет рассмотрен случай, когда отношение имеет
два или более потенциальных ключа.
Итак, ниже дается предварительное и весьма неформальное определение ЗНФ.
■ ■BBBBBBB Отношение находится в третьей нормальной форме тогда и только тогда,
когда неключевые атрибуты (если они есть вообще) являются
а) взаимно независимыми;
б) неприводимо зависимыми от первичного ключа.
Смысл понятий "неключевые атрибуты" и "взаимно независимые атрибуты"
