Дейт К. Введение в системы баз данных
Подождите немного. Документ загружается.


дальнейшее обсуждение данного вопроса.
Переменные отношений
В своей первой статье [4.1] Кодд говорил об "изменяющихся со временем"
отношениях. Под этим термином он подразумевал то, что выше в этой главе мы
назвали переменными отношений, т.е. переменными, значения которых являются
отношениями (в общем случае в разное время различными отношениями).
Например, как уже отмечалось, выражение
CREATE BASE RELATION S ... ;
определяет переменную с именем s, значение которой в любой момент времени
является, как определено выше, отношением. Однако это значение "изменяется со
временем", так как со временем будут вставляться новые кортежи поставщиков
и/или существующие кортежи поставщиков будут модифицироваться или удаляться
(отсюда, как следствие, кардинальное число также будет "изменятся со временем").
Однако "изменяющийся со временем" — не очень удачный термин. В конце
концов, если в некотором языке программирования используется приведенное выше
объявление
DECLARE QTY INTEGER ...;
то переменную QTY мы будем называть не "изменяющимся со временем" целым
числом, а переменной целого типа. Поэтому в данной книге будет использоваться
термин "переменная отношения"; однако читатель должен знать о существовании и
другого термина.
Теперь пусть R — переменная отношения; переменная R будет иметь разные
значения в разное время. Однако все возможные значения переменной R будут
иметь одинаковые заголовки. Например, все возможные значения базового
отношения S будут иметь заголовок {S#,SNAME,STATUS,CITY}.
2[2]
И еще о терминологии
Как мы уже объясняли, количество атрибутов в данном отношении называется
степенью (иногда называют арностью) отношения. Отношение первой степени
называется унарным, отношение степени 2 —- бинарным, отношение степени 3 —
тернарным ... и отношение степени п — п-арным. (В общем случае в реляционной
модели рассматриваются n-арные отношения, где п — произвольное
неотрицательное целое число.) В базе данных поставщиков и деталей отношения S,
P и SP имеют степень 4, 5 и 3, соответственно.
Иногда возникает неясность из-за схожести понятий домена и унарного
отношения (ведь домен выглядит как раз как таблица с одним столбцом). Однако
заметьте, что существует довольно существенная разница между этими двумя
понятиями: домены статичны, а отношения динамичны (здесь под отношением мы
понимаем переменную отношения). Другими словами, содержимое (переменной)
отношения изменяется со временем, а содержимое домена — нет (вспомним, что
2[2]
Для читателей, знакомых с языком SQL, отметим, что в SQL существует возможность
добавлять новый столбец или удалять существующий столбец из базовой таблицы посредством
оператора ALTER TABLE. Однако эту операцию лучше рассматривать не как изменение
существующей таблицы, а как уничтожение существующей таблицы и создание новой с тем же
именем и новым заголовком.
домен содержит все возможные значения подходящего типа). Более подробное
обсуждение этого вопроса смотрите в [4.8].
"Не различные домены"
Вернемся вновь к определению отношения; обратите внимание, что лежащие в
основе отношения домены не обязательно все различны. Это значит, что несколько
атрибутов в отношении могут иметь основой один домен. Пример такого отношения
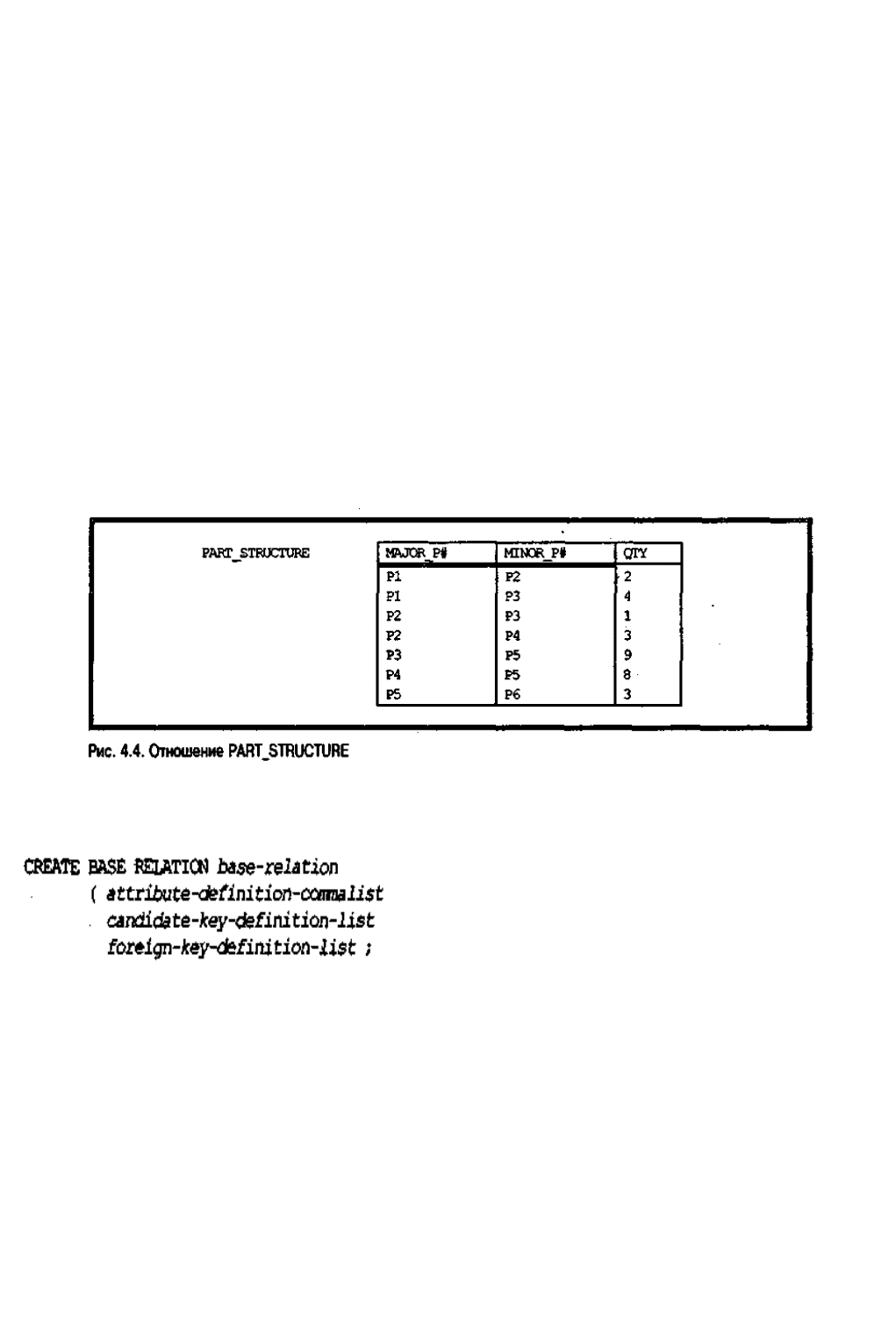
показан на рис. 4.4. (Это отношение названо PART_STRUCTURE.)
Если один и тот же домен используется более одного раза в одном и том же
отношении, то, как указывалось ранее, нельзя дать всем атрибутам имена,
совпадающие с именами лежащих в их основе доменов. На рис. 4.4 показан
рекомендуемый в такой ситуации подход: называть атрибуты по-разному, так,
чтобы в качестве префикса у этих имен было "ролевое" имя атрибута, а в качестве
суффикса — имя домена. Действительно, если условиться всегда следовать этому
правилу, а также всегда использовать одинаковые символы разделения (например,
такие как символ подчеркивания), чтобы отделять ролевое имя (если оно есть) от
имени домена, то нам при определении атрибута никогда не понадобится в явном
виде спецификация "DOMAIN (domain)" (об этом подробнее в следующем разделе).
Определение данных
Вот синтаксис оператора create base relation:
При выполнении этого оператора создается новое базовое отношение с именем
base-relation, а также указанные атрибуты, потенциальные и внешние ключи.
Отношение создается пустым (т.е. не содержит кортежей). Несколько примеров
использования этого оператора вы найдете на рис. 4.3. Ниже приводятся некоторые
пояснения к оператору.
1. 1. Термины list (список) и commalist (список, разделенный запятыми)
удобно использовать при описании операторов (они будут использоваться здесь и
далее в книге). В общем они значат следующее:
• •BBBBB Если xyz — синтаксическая единица, то xyz-list -— это
синтаксическая единица, которая состоит из последовательности единиц
xyz, количество которых больше либо равно нулю, причем каждые две
единицы xyz между собой разделены по крайней мере одним пробелом.

• •BBBBB Если xyz— синтаксическая единица, то xyz-commalist — это
синтаксическая единица, которая состоит из последовательности единиц
xyz, количество которых больше либо равно нулю, причем каждые две
единицы xyz между собой разделены запятой (и возможно, одним или
несколькими пробелами).
Так, например, список определения атрибутов attribute-defenition-
commalist состоит из последовательности единиц attribute-defenition
(т.е. определений атрибутов), каждая из которых, за исключением последней,
отделяется от следующей запятой, а список определения потенциальных ключей
candidate-key-definition-list состоит из последовательности единиц
candidate-key-definition (т.е. определений потенциальных ключей),
каждая из которых, за исключением последней, отделяется от следующей по
крайней мере одним пробелом. То же самое можно сказать о списке определения
внешних ключей foreign-key-definition-list.
Замечание. Здесь и далее мы будем опускать дефисы из таких выражений, как
"candidate key definition" (за исключением формального синтаксиса), конечно, если
при этом не возникает неясности.
2. 2. Определение атрибута имеет следующую форму:
attribute DOMAIN (domain)
Если опустить спецификацию "DOMAIN (domain)", то считается, что
атрибут основан на домене с тем же именем.
3. 3. Определение потенциальных ключей подробно объясняется в
следующей главе. А пока будем просто предполагать, что в каждом операторе create
base relation есть только одно определение в следующей форме:
PRIMARY KEY (attribute-commalist)
4. 4. Определения внешних ключей также объясняются в следующей главе.
Удаление базовых отношений. Вот синтаксис оператора удаления
существующего базового отношения:
DESTROY BASE RELATION base-relation ;
Эта операция предназначена для удаления всех кортежей указанного базового
отношения о последующим удалением всех записей в каталоге об этом отношении.
После этого отношение больше не 'известно системе. (Если нет указания, то мы
предполагаем, что операция DESTROY BASE RELATION просто не будет
выполняться, если существует определение представления, которое ссылается на
удаляемое базовое отношение. Дальнейшее обсуждение этого вопроса приводится в
следующих частях книги,)
Свойства отношений
У отношений есть определенные свойства, все они являются
непосредственными свойствами данного ранее определения отношения, и все они
имеют очень важное значение. Мы сначала кратко укажем эти свойства, а затем
подробно их обсудим. Речь идет о перечисленных ниже четырех свойствах. В
любом отношении
■ ■BBBBBBB нет одинаковых кортежей;
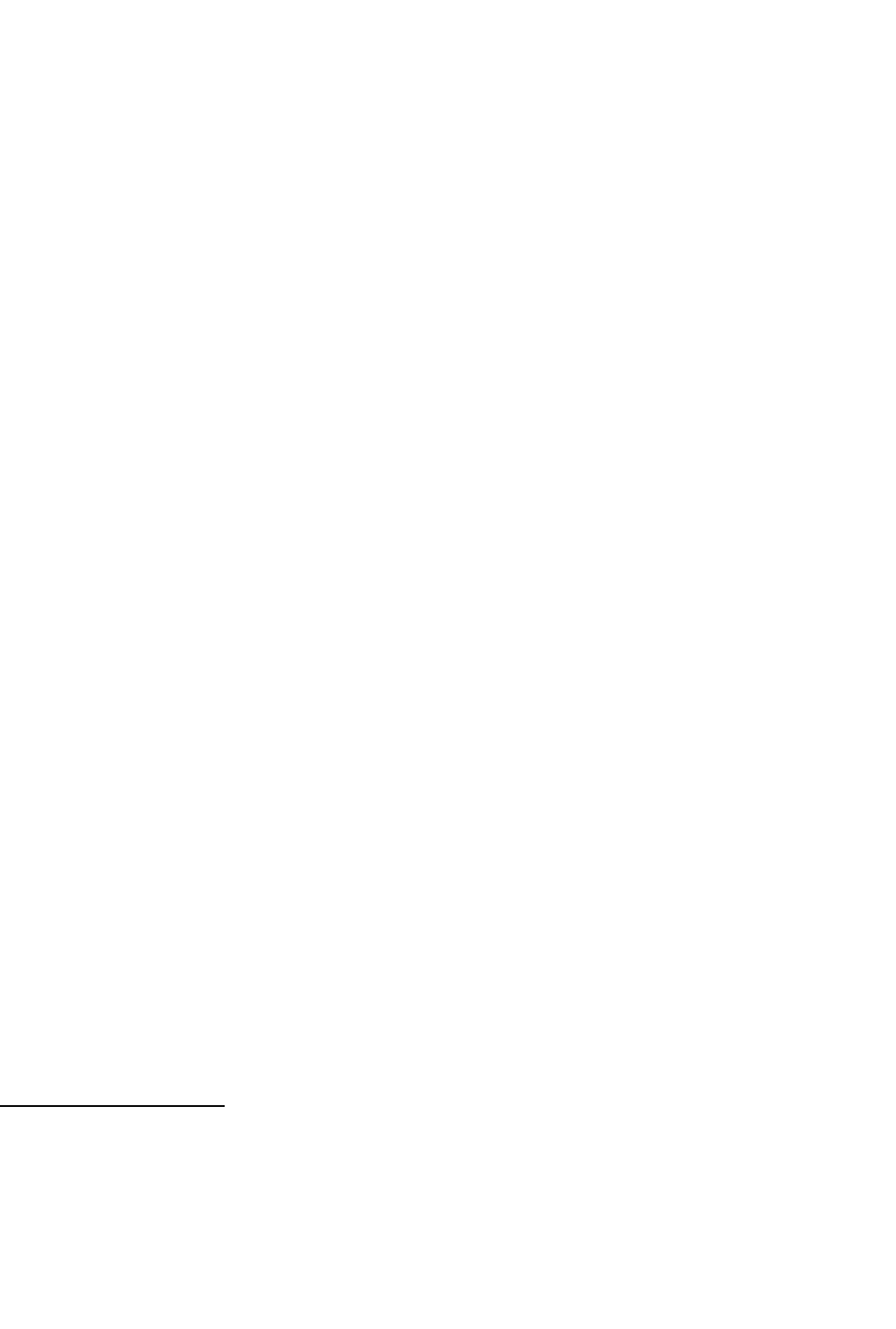
■ ■BBBBBBB кортежи не упорядочены сверху вниз;
■ ■BBBBBBB атрибуты не упорядочены слева направо;
■ ■BBBBBBB все значения атрибутов атомарные.
1. 1.BBBBBB Нет одинаковых кортежей.
Это свойство следует из того факта, что тело отношения — это математическое
множество (кортежей), а множества в математике по определению не содержат
одинаковых элементов.
Между прочим, первое свойство служит хорошей иллюстрацией того, что
отношение и таблица — это не одно и то же, так как таблица (в общем случае)
может содержать одинаковые строки при отсутствии правил, запрещающих это, в то
время как отношение не может содержать одинаковых кортежей. (Потому
"отношение", содержащее одинаковые кортежи, не будет отношение по
определению) К большому сожалению, стандарт SQL допускает, чтобы таблицы
содержали одинаковые строки. Здесь было бы неуместным обсуждать все причины
того, почему одинаковые строки — это ошибка (развернутое обсуждение этого
вопроса приводится в [4.5,4.11]); для наших целей достаточно остановиться на том,
что реляционная модель не допускает одинаковых строк; здесь и далее в этой книге
мы также предполагаем, что одинаковые строки не допустимы. (Это замечание
касается в основном обсуждения языка SQL в главе 8. При рассмотрении самой
реляционной модели, конечно, никаких предположений делать не надо.)
Важным следствием того факта, что не существует одинаковых строк, является
то, что всегда существует первичный ключ
3[3]
. Так как кортежи уникальны, то по
крайней мере комбинация всех атрибутов будет обладать свойством уникальности, а
значит, при необходимости может служить первичным ключом. На практике,
конечно, обычно нет необходимости использовать все атрибуты — подходит
комбинация из нескольких атрибутов. В главе 5 будет дано определение первичного
ключа, как не включающего в себя атрибуты, излишние с точки зрения
уникальности; поэтому, например, комбинация {S#,CITY} хотя и "уникальна", но
она не является первичным ключом, так как мы можем убрать атрибут CITY, не
нарушив уникальности. (Однако заметьте, что первичные ключи могут быть
составными. Примером тому может служить отношение SP.)
1. 2.BBBBBB Кортежи не упорядочены (сверху вниз).
Это свойство также следует из того, что тело отношения — это математическое
множество, а простые множества в математике не упорядочены. Например, на рис.
4.1 кортежи отношения S могли быть расположены в противоположном порядке —
это было бы тем же самым отношением. Поэтому в отношении нет понятий "пятого
кортежа", “97-го кортежа" или "первого кортежа"; т.е. нет понятия позиционной
адресации и понятия "последовательности".
4[4]
В статье [4.11], которая уже
3[3]
Точнее, всегда существует по крайней мере один потенциальный ключ. Мы предполагаем, что
один из потенциальных ключей выбран как первичный. Дальнейшее обсуждение этого вопроса
приведено в главе 5.
4[4]
Понятие "последовательности" требуется для интерфейса между реляционной базой данных и
базовым языком, таким как С или COBOL. Но это требование для базовых языков, а не для
реляционной модели. В сущности, эти языки требуют, чтобы неупорядоченные множества были
преобразованы в упорядоченные таким образом, чтобы могли выполняться операции типа
"вызвать следующий кортеж". Заметьте также, что такие возможности составляют часть
прикладного программного интерфейса—они не видны конечному пользователю.

упоминалась в связи со свойством "нет одинаковых кортежей", показано, почему
свойство "кортежи не упорядочены" также имеет важное значение (в
действительности эти свойства взаимосвязаны).
Как уже отмечалось в этом разделе, второе свойство отношений также служит
иллюстрацией того факта, что отношение и таблица— это не одно и то же, так как
строки таблицы упорядочены сверху вниз, в то время как кортежи отношения —
нет.
2. 3.BBBBBB Атрибуты не упорядочены (слева направо).
Это свойство следует из того факта, что заголовок отношения также определен
как множество (атрибутов). Например, на рис. 4.1 атрибуты отношения S могли
быть представлены, скажем, в таком порядке: SNAME, CITY, STATUS, S# — это
было бы то же самое отношение, по крайней мере с точки зрения реляционной
модели. Поэтому не существует понятий "первого атрибута" или "последнего
атрибута" (и т.д.), не существует "следующего атрибута" (опять же нет понятия
"последовательности"); иначе говоря, атрибут всегда определяется по имени, а не по
расположению. Это позволяет избежать некоторых ошибок и неясности при
написании программ. Например, не существует (или не должно существовать)
возможности сбоя системы из-за "залезания" одного атрибута на другой. Эта
ситуация отличается от ситуации во многих системах программирования, где можно
использовать физическую смежность логически дискретных элементов (умышленно
или случайно) различными методами, потенциально способными повредить
систему.
Заметим, что вопрос порядка атрибутов— это еще одна область, где конкретное
представление отношения в виде таблицы предполагает неверные факты: столбцы
таблицы упорядочены слева направо, а атрибуты отношения — нет.
3. 4.BBBBBB Все значения атрибутов атомарные.
Последнее свойство является следствием того, что все лежащие в основе
домены содержат только атомарные значения. Это свойство можно выразить и
иначе (довольно неформально): в каждой позиции пересечения столбца и строки в
таблице расположено в точности одно значение, а не набор значений. Можно
сказать еще и так: отношения не содержат групп повторения. Отношение,
удовлетворяющее этому условию, называется нормализованным, или
представленным в первой нормальной форме (другие нормальные формы — вторая,
третья — обсуждаются в следующих частях книги).
Сказанное означает, что с точки зрения реляционной модели все отношения
нормализованы. Это значит, что термин "отношение" всегда означает
"нормализованное отношение" в контексте реляционной модели. Но дело в том, что
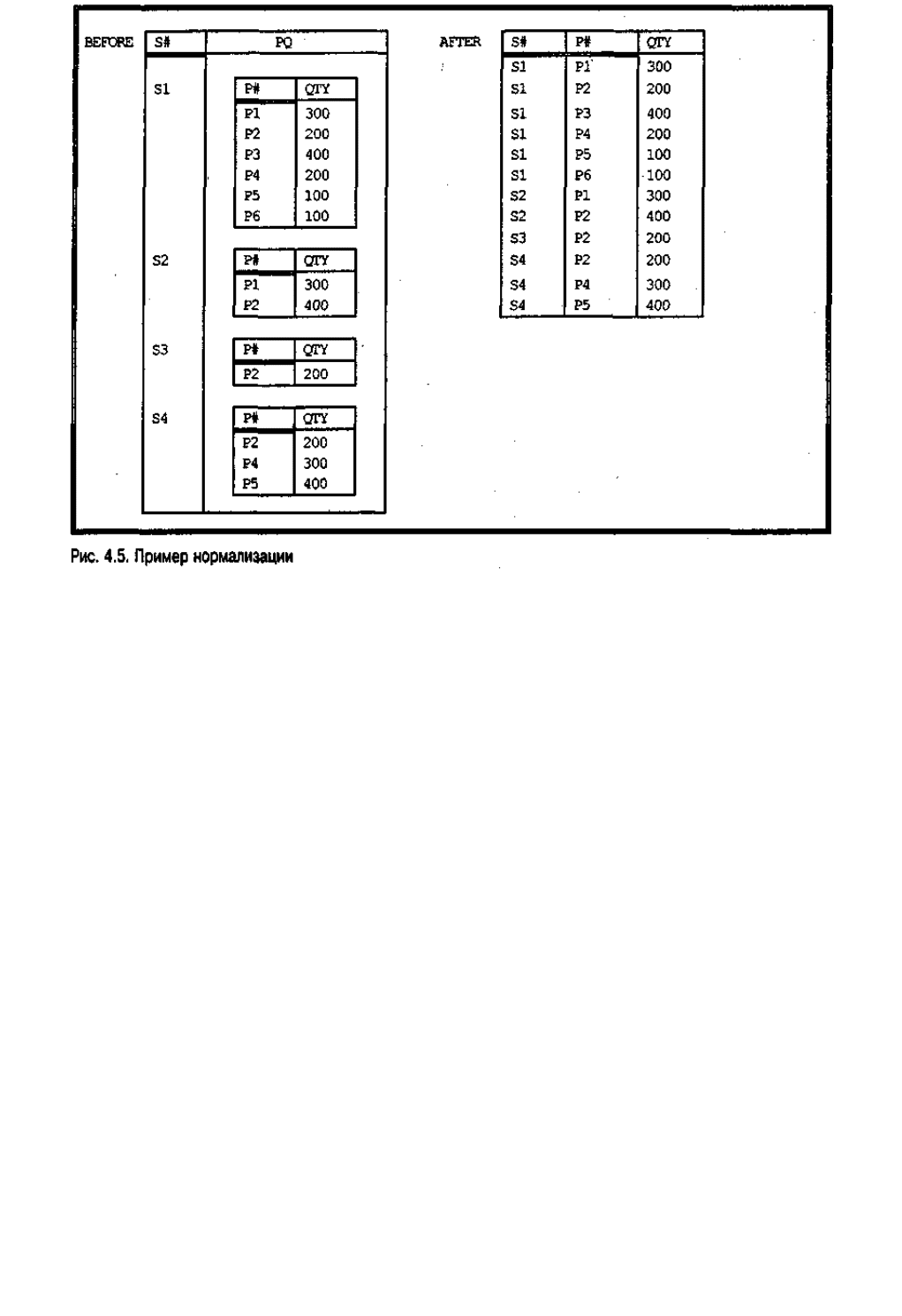
математическое отношение вовсе не обязано быть нормализованным. Рассмотрим
отношение BEFORE, изображенное на рис. 4.5. С математической точки зрения
BEFORE является отношением степени два, в одном из доменов этого отношения
значениями являются отношения.
Следовательно, элементы этого домена сами являются отношениями, а не
простыми скалярами. В этом примере атрибут PQ определен на основе домена со
значениями-отношениями, элементами которого являются бинарные отношения; эти
бинарные отношения определены, в свою очередь, на основе двух доменов со
скалярными значениями, а именно доменов Р# и QTY. Реляционная модель не
допускает доменов со значениями-отношениями (это еще будет обсуждаться далее в
этой книге).
Отношение, подобное отношению BEFORE, не допустимо в реляционной базе
данных. Оно должно быть заменено нормализованным отношением, содержащим ту
же самую информацию. Таким отношением является отношение AFTER на рисунке
(в действительности это уже знакомое нам отношение SP). Степень отношения
AFTER равна трем, и в его основе лежат три домена со скалярными значениями. Как
уже объяснялось, отношение, подобное отношению AFTER, называется
нормализованным; отношение, подобное отношению BEFORE, называют
ненормализованным; а процесс преобразования отношения BEFORE в отношение
AFTER называется нормализацией. Как показано в этом примере, получить
нормализованную форму из ненормализованной довольно просто, однако о
процессе нормализации следует сказать еще многое, и это еще будет обсуждаться
далее в книге.

Причина, по которой требуется нормализация всех таблиц, состоит в
следующем. С математической точки зрения нормализованное отношение имеет
более простую структуру. Вследствие этого требуется меньше операторов для
работы с нормализованными отношениями и они проще. Например, рассмотрим две
задачи.
1. 1.BBBBBB Записать новую информацию о поставке для поставщика S5 деталей Р5 в
количестве 500.
2. 2.BBBBBB Записать новую информацию о поставке для поставщика S4 деталей Р5 в
количестве 500.
Для отношения AFTER нет существенной разницы в выполнении этих двух
операций, каждое из них требует вставки одного кортежа в отношение. А для
отношения BEFORE первая задача требует такой же вставки кортежа в отношение,
но вторая задача требует существенно отличную операцию, а именно: вставку новой
записи в набор записей (т.е. группу повторения) внутри существующего кортежа.
Поэтому для поддержки ненормализованных операций нужны два совершенно
разных оператора "INSERT". По аналогичным причинам также понадобятся два
различных оператора "UPDATE", два различных оператора "DELETE" и т.д.
Обратите внимание, что эти замечания касаются не только операторов обработки
данных, но и всех операторов системы; например, нужны дополнительные
операторы обеспечения безопасности данных, нужны дополнительные операторы
обеспечения целостности данных и т.п. (И вообще, можно считать аксиомой то, что
если у нас есть п путей представления данных, то нам потребуется п наборов
операций.) Итак, ответ из одного слова на вопрос "Почему мы настаиваем на
нормализации?" — это простота: простота объектов, с которыми мы работаем, что
приводит к упрощению всей системы.
4.4. 4.4. Виды отношений
В этом разделе мы определим некоторые из видов отношений, встречающихся
в реляционных системах (однако обратите внимание, что не все системы
поддерживают каждый из этих видов).
1. 1.BBBBBB Прежде всего, именованное отношение — это переменная отношения,
определенная в СУБД посредством операторов CREATE BASE RELATION,
CREATE VIEW и CREATE SNAPSHOT (в используемом нами синтаксисе). Об
операторе CREATE VIEW рассказывалось в главе 3, а об операторе CREATE
SNAPSHOT речь пойдет далее в этой главе.
2. 2.BBBBBB Базовым отношением называется именованное отношение, которое не
является производным (т.е. базовое отношение является автономным). На практике
базовые — это те отношения, которые считаются достаточно важными (среди
рассматриваемых в базе данных), и проектировщик базы данных счел нужным дать
им название и сделать их непосредственной частью базы данных, в отличие от
менее важных временных отношений (таких как, например, результат запроса).
3. 3.BBBBBB Производным отношением называется отношение, определенное
(посредством реляционного выражения) через другие именованные отношения и, в
конечном счете, через базовые отношения.
Предостережение. Помните, что некоторые авторы под "производным"
подразумевают "выражаемое" (смотрите следующий пункт).

4. 4.BBBBBB Выражаемым отношением называется отношение, которое можно
получить из набора именованных отношений посредством некоторого реляционного
выражения. Конечно, каждое именованное отношение является выражаемым
отношением, но не наоборот. Базовые отношения, представления, снимки (об этом
ниже), промежуточные и окончательные результаты отчетов — все это выражаемые
отношения. Иначе говоря, множество всех выражаемых отношений — это в
точности множество всех базовых отношений и всех производных отношений.
5. 5.BBBBBB Представлением называется именованное производное отношение.
(Представления, как и базовые отношения, являются переменными отношений.)
Представления виртуальны — они представлены в системе исключительно через
определение в терминах других именованных отношений.
6. 6.BBBBBB Снимки (snapshot) — это именованные производные отношения, такие
же как представления (и подобно представлениям они являются переменными
отношений). Однако в отличие от представлений снимки реальны, а не виртуальны,
т.е. представлены не только с помощью определения в терминах других
именованных отношений, но и также (по крайней мере концептуально) своими
отдельными данными. Вот пример:
Создание снимка похоже на выполнение запроса, за исключением того, что
результат такого запроса сохраняется в базе данных под определенным именем (SC
в нашем примере) как отношение, доступное только для чтения, и периодически (в
нашем примере — каждый день) снимок "обновляется", т.е. его текущее значение
сбрасывается, запрос выполняется снова и его результат становится новым
значением снимка. Применение снимков будет обсуждаться в следующих частях
книги.
7. 7.BBBBBB Результатом запроса называется неименованное производное
отношение, служащее результатом некоторого определенного запроса, База данных
не обеспечивает постоянного существования для результатов запросов (чтобы
сохранить результат запроса, его можно присвоить некоторому именованному
отношению).
8. 8.BBBBBB Промежуточным результатом называется неименованное производное
отношение, являющееся результатом некоторого реляционного выражения,
вложенного в другое, большее выражение. Например, рассмотрим такое выражение:
Отношение, являющееся результатом выражения S JOIN SP будет
промежуточным результатом; назовем его TEMP1. Тогда отношение, являющееся
результатом выражения TEMP1 WHERE P# = 'P2', также будет промежуточным
результатом; назовем его TEMP2. А отношение, являющееся результатом выражения
TEMP2 [S#, CITY], будет окончательным результатом. База данных не
обеспечивает постоянного существования для промежуточных результатов, как и
для окончательных результатов (в действительности, как уже упоминалось в главе 3,
они могут не существовать в виде полной материализованной таблицы как таковой).
9. 9.BBBBBB И наконец, хранимым отношением называется отношение, которое
поддерживается в физической памяти "непосредственным" образом (конечно, при

подходящем определении "непосредственности"; более подробное обсуждение
этого вопроса выходит за рамки данной главы).
В заключение добавим, что хранимое отношение не всегда совпадает с базовым
отношением. Набор хранимых отношений должен быть таким, чтобы все базовые
отношения, а значит, и все выражаемые отношения можно было произвести из него;
но при этом не требуется, чтобы все хранимые отношения были базовыми
отношениями, и не требуется, чтобы все базовые отношения были хранимыми.
Более подробное обсуждение этого вопроса было приведено в главе 3.
4.5. 4.5. Отношения и предикаты
Хотя мы не останавливались на этом вопросе, читатель, наверное, интуитивно
понимает, что каждое отношение имеет некоторую интерпретацию, причем
пользователи должны знать ее для эффективного использования базы данных.
Например, интерпретация отношения S может быть следующей:
Поставщик с определенным номером (S#) имеет определенное имя (SNAME) и
определенное значение статуса (STATUS) и располагается в определенном городе
(CITY); кроме того, нет двух поставщиков с одинаковыми номерами.
Это утверждение не очень точное, но оно подходит для наших целей.
Формально, предыдущее утверждение — это пример того, что называют
предикатом, или функцией значения истинности; в нашем конкретном случае —
функцией четырех аргументов. Подстановка значений этих аргументов
эквивалентна вызову функции (или "подтверждению" предиката), а значит,
получению выражения, называемого высказыванием, которое может быть либо
истиной либо ложью. Например, при подстановке
S#= 'SI' SNAME ='Smith1 STATUS = 20 CITY = 'London'
получим высказывание, являющееся истиной. А при подстановке
S#= 'SI' SNAME = 'Abbey' STATUS = 45 CITY = 'Tucson'
получим высказывание, являющееся ложью (потому что поставщик с номером S1
имеет имя не Abbey, статус не 45 и располагается не в Туксоне). И в любой момент
времени отношение содержит в точности те кортежи, при которых предикат
является истиной.
Из вышесказанного следует, что (например) кортеж, представленный в качестве
кандидата для вставки в некоторое отношение, будет принят СУБД только в том
случае, если он не противоречит соответствующему предикату (т.е.
соответствующее высказывание не будет ложью). Вообще предикат данного
отношения составляет критерий возможности обновления для этого отношения;
т.е. критерий для решения, является ли некоторое обновление допустимым (или по
крайней мере "правдоподобным") для данного отношения.
Для того чтобы система могла определить допустимость обновления данного
отношения, ей должен быть известен предикат этого отношения. Конечно, сейчас
СУБД не может в точности знать предикат для данного отношения. Например, в
случае отношения S СУБД не может знать точно, что предикат для кортежа
(S1,Smith,20,London) будет истиной, а для кортежа (S1,Abbey,45,Tucson) — нет.
5[5]
5[5]
Здесь мы используем очевидное сокращение, согласно которому выражение
(S1,Smith,20,London) соответствует кортежу {<S#:'S1'>, <SNAME:'Smith'>, <STATUS:20>, <CITY:

Однако СУБД считает кортеж приемлемым, если выполнены следующие условия:
• •BBBBBBBBBB Значение S# принадлежит домену номеров поставщиков.
• •BBBBBBBBBB Значение SNAME принадлежит домену имен.
• •BBBBBBBBBB Значение STATUS принадлежит домену значений статуса.
• •BBBBBBBBBB Значение CITY принадлежит домену названий городов.
• •BBBBBBBBBB Значение S# должно быть уникальным среди всех значений отношения.
Иначе говоря, для базового отношения, такого как S, в СУБД используются
определенные, объявленные для этого отношения, правила целостности, такие как
правило о том, что значение S# уникально и принадлежит домену номеров
поставщиков. Поэтому формально мы можем определить "значение" (известное
СУБД) данного базового отношения как логическое умножение (логическая
операция И) всех известных СУБД применяемых к этому отношению правил. И
именно в этом смысле СУБД будет проверять допустимость обновления данного
отношения.
Мы будем еще несколько раз возвращаться к значению отношения в
последующих главах.
4.6. 4.6. Реляционные базы данных
Исходя из обсуждений и объяснений этой главы, можно дать более формальное
определение (более формальное, чем данное выше в этой главе) термина
"реляционная база данных". Перефразировав определение, данное Коддом в [4.1],
Получим следующее:
Реляционная база данных — это база данных, воспринимаемая пользователем
как набор нормализованных отношений (т.е. переменных отношений) разной
степени.
Как отмечалось ранее, выражение "воспринимаемая пользователем" является
решающим: идея реляционной модели применяется к внешнему и концептуальному
уровням системы, а не к внутреннему уровню. Можно сказать и иначе —
реляционная модель представляет систему баз данных на уровне абстракции,
несколько удаленном от подробностей лежащей в основе этой системы машины; так
же как, например, язык Pascal представляет систему программирования на уровне
абстракции, несколько удаленном от подробностей лежащей в основе этой системы
машины. В действительности реляционную модель можно рассматривать как язык
программирования, специально, ориентированный на приложения баз данных.
Различие между доменами и (именованными) отношениями также можно
несколько уточнить. Мы называем именованные отношения переменными, так как
их значения изменяются со временем. Как указывалось выше в этой главе, домены
не являются переменными в этом смысле. Например, множество всех возможных
номеров поставщиков, конечно, не изменяется со временем, или если изменяется, то
изменение носит описательный характер, т.е. происходит на уровне типа, а не
экземпляра. Это немного похоже на изменение основного типа данных для номера
поставщиков с CHAR(5) на CHAR(7). Обратите внимание, что такое изменение,
возможно, повлечет за собой реорганизацию базы данных.
Итак, можно сказать, что в традиционных терминах отношение соответствует
файлу (логическому, а не физическому), кортеж — записи (экземпляру, а не типу),
'London'>}.
