Дейт К. Введение в системы баз данных
Подождите немного. Документ загружается.


Часть
III
Проектирование базы данных
В этой части речь пойдет о проектировании базы данных, точнее, о проектировании
реляционной базы данных. В общем проблема формулируется следующим образом:
как в некоторой базе данных для заданного набора данных выбрать подходящую
логическую структуру? Иначе говоря, нужно решить вопрос, какие базовые
отношения и с какими атрибутами следует задать. Большое практическое значение
решения этой проблемы очевидно.
Приступая к подробному изложению этой темы, отметим следующие
особенности.
■ ■BBBBBBB Прежде всего следует заметить, что речь здесь пойдет о логическом, а не
физическом макете. Это вовсе не значит, что физический макет не имеет
большого значения, наоборот его значение очень велико. Однако, несмотря на
это, нужно сделать следующие оговорки.
▪ ▪BBBBBBBBBBB Физический макет может рассматриваться как отдельная сопутствующая
часть. Иначе говоря, для "правильного" составления макета базы данных
следует прежде всего создать логический (т.е. реляционный) макет, а затем в
виде отдельного шага отобразить этот логический макет на некоторые
физические структуры, поддерживаемые СУБД.
▪ ▪BBBBBBBBBBB Физический макет по определению является специфическим для данной
СУБД, однако его обсуждение выходит за рамки этой книги. Логический
макет, наоборот, совершенно независим от СУБД, и для его реализации
могут быть использованы некоторые строгие теоретические принципы.
Именно эти принципы и будут описаны в данной книге.
К сожалению, на практике часто случается так, что реализация макета на физическом уровне может оказывать существенное обратное влияние
на логический макет. Иначе говоря, в таком случае для достижения компромисса следует выполнить несколько циклов проектирования
"логический макет — физический макет". Тем не менее, изложение материала в этой части ведется исходя из необходимости создания
логического макета без учета особенностей физической организации, т.е. без учета требований к высокой производительности. Таким образом,
основная цель этой части книги — "первоочередное создание логического макета".
■ ■BBBBBBB Хотя, как уже отмечалось ранее, речь в основном пойдет о реляционном
макете, представленные здесь идеи также в равной степени относятся и к
нереляционным базам данных. Иначе говоря, при создании макета данных в
нереляционной системе следует прежде всего создать реляционный макет, а
затем на отдельном следующем этапе отобразить этот реляционный макет на
любые нереляционные структуры (например, иерархии), поддерживаемые в
СУБД.
■ ■BBBBBBB После всего сказанного следует подчеркнуть, что проектирование базы
данных скорее искусство, чем просто наука. Конечно, существуют некоторые
научные принципы составления таких макетов, и они будут изложены в
следующих трех главах. Однако при проектировании базы данных возникает
множество других проблем, которые не всегда можно охватить этими
принципами. В результате теоретики и практики в области создания баз данных
разработали большое число методологий проектирования. Среди них есть как

достаточно точные и строгие, так и не очень, однако все они
специализированные и предназначены для решения именно той проблемы,
которая считалась неразрешимой к моменту создания данной конкретной
методики. Иными словами, они были задуманы для поиска такого логического
макета, который был бы, бесспорно, лучшим в данной ситуации. Поскольку все
эти методологии являются в большей или меньшей степени
специализированными, существует мало объективных критериев для
предпочтения одной из них. Все же, несмотря на это, в главе 12 будет описан
один широко известный подход, менее специализированный, чем другие.
■ ■BBBBBBB Следует также отметить некоторые допущения, используемые в дальнейшем
изложении.
▪ ▪BBBBBBBBBBB Проектирование базы данных — это не единственное условие получения
правильной организации структуры данных, помимо этого ключевым
условием является также целостность данных.
▪ ▪BBBBBBBBBBB Далее в большинстве Случаев макет рассматривается независимо от
приложения. Иначе говоря, интерес представляют сами данные, а не то, как
они используются. Независимость от приложения желательна потому, что
обычно в момент проектирования базы данных не известны все возможные
способы использования данных. Таким образом, необходимо, чтобы макет
был стабильным, т.е. оставался работоспособным даже при возникновении в
приложении новых (т.е. неизвестных на момент создания исходного макета)
требований к данным. Следуя этим допущениям (и используя терминологию
предыдущих глав), нужно создать концептуальную схему, т.е. абстрактный
логический макет, не зависящий от аппаратного обеспечения, операционной
системы, СУБД, языка программирования, пользователя и т.д. В частности,
как уже указывалось ранее, не будет проявляться никакого интереса к поиску
компромиссных решений для достижения повышенной производительности.
■ ■BBBBBBB Как отмечалось выше, задача проектирования базы данных заключается в
том, чтобы решить, какие базовые отношения и с какими атрибутами следует
использовать. Фактически для этого также необходимо выяснить, какие домены
следует использовать. К моменту создания книги этой теме было посвящено
совсем немного публикаций, поэтому описание данного вопроса будет очень
кратким.
В главе 9 описаны некоторые теоретические основы, а в главах 10, 11 —
основные идеи дальнейшей нормализации, которые позволяют придать смысл
неформальным утверждениям о преимуществах того или иного макета. Затем в
главе 12 приведены концепции модели объект/отношение и показано, как эти
концепции можно использовать для построения макета "сверху вниз" (начиная с
реальных объектов и заканчивая формальным макетом базы данных).

Глава 9
Функциональные
зависимости
15. 9.1. Введение
В этой главе представлена концепция функциональной зависимости (functional
dependency— FD), которая если "не совсем фундаментальна, то очень близка к
таковой". Эта концепция лежит в основе обсуждаемых в следующих главах тем,
включая, в частности, теорию проектирования базы данных, описанную в главе 10.
По сути, функциональная зависимость (далее для ее обозначения часто будет
использоваться аббревиатура ФЗ) является связью типа многие-к-одному между
множествами атрибутов внутри данного отношения. Например, для отношения
поставок SP существует функциональная зависимость между множеством атрибутов
(S#, P#} и {QTY}, т.е. многим значениям пары атрибутов S#—Р# соответствует
одно значение атрибута QTY (для проверки этого утверждения можете обратиться
§3 рис. 3.8).
В этой главе концепция функциональной зависимое, определяется более точно, с
разделением функциональных зависимостей на выполняемые в некоторых частных
случаях и выполняемые всегда. Как уже говорилось выше, ФЗ обеспечивает основу
для научного подхода к решению нескольких практических задач, поскольку
обладает богатым набором интересных формальных свойств, позволяющих
формально и строго решить многие проблемы. Ниже будут подробно описаны
некоторые из этих формальных свойств и даны объяснения по поводу их
практического применения. В конце главы представлено краткое резюме.
Замечание. При первом чтении этой главы многие разделы можно пропустить,
поскольку большая часть материала, необходимого для понимания изложенного в
следующих главах, содержится в первых нескольких разделах главы. Поэтому все
остальные разделы можно лишь просмотреть, а затем вновь вернуться к ним,
ознакомившись со всеми тремя главами этой части.
16. 9.2. Основные определения
Для демонстрации основных идей данного раздела используется несколько
измененная версия отношения поставок, которое в дополнение к обычным
атрибутам S#, P# и QTY будет содержать также атрибут CITY, представляющий
город соответствующего поставщика. Во избежание путаницы далее это измененное
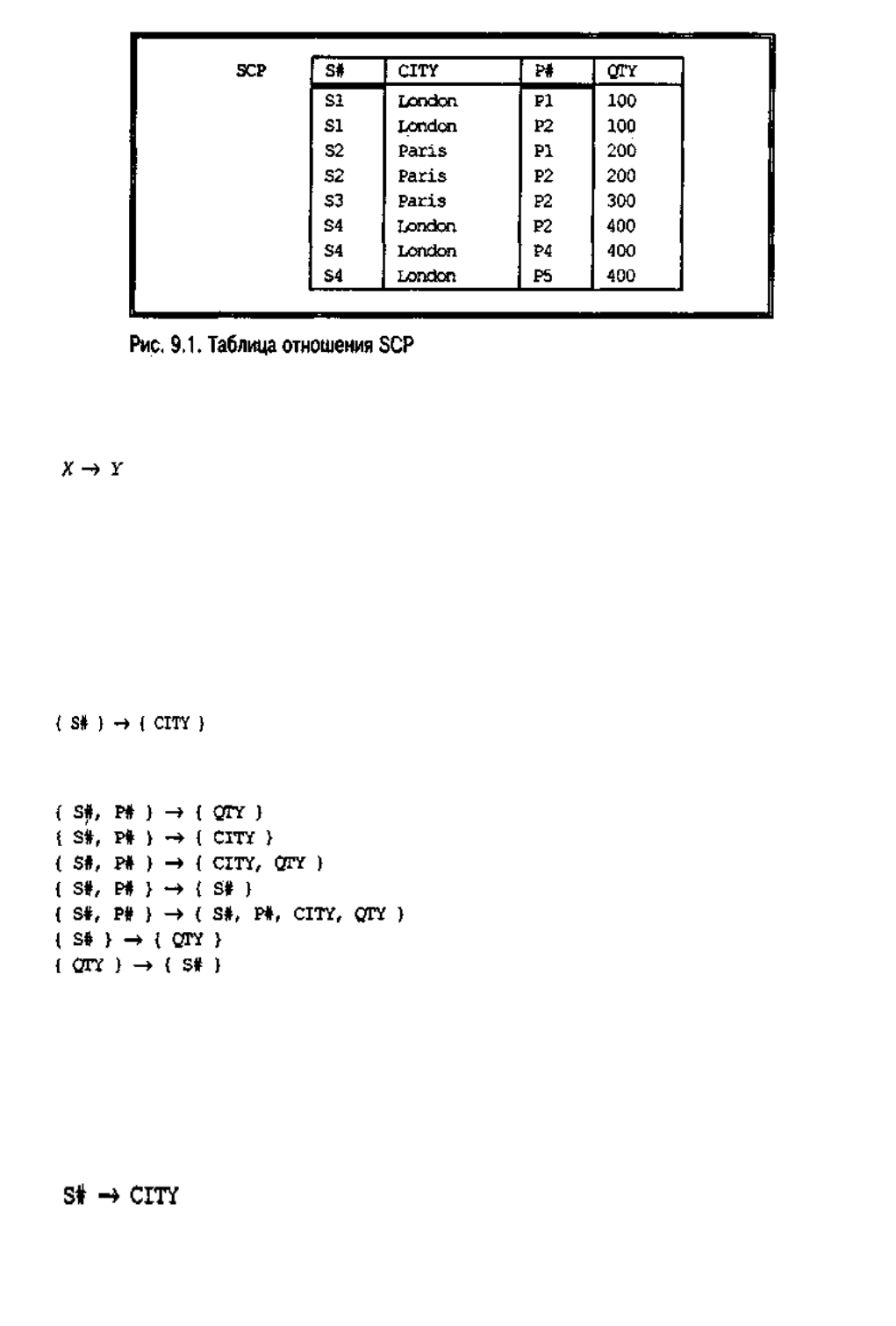
отношение будет называться SCP. Оно в виде таблицы представлено на рис. 9.1.
Следует четко различать: а) значение этого отношения (т.е. значение переменной
отношения) в определенный момент времени; б) набор всех возможных значений,
которые данное отношение (переменная) может принимать в различные моменты
времени (подробнее это описано в главе 4). Сначала дадим определение концепции
функциональной зависимости для пункта (а), а затем для пункта (б).
■ ■BBBBBBB Пусть R— это отношение, а X и У— произвольные подмножества множества
атрибутов отношения R. Тогда Y функционально зависимо от X, что в
символическом виде записывается как
(и читается либо как функционально определяет Y", либо как "X стрелка Y"),
тогда и только тогда, когда каждое значение множества X отношения R связано в
точности с одним значением множества Y отношения R.
Иначе говоря, если два кортежа отношения R совпадают по значению X, они
также совпадают и по значению Y. Например, таблица отношения SCP (см. рис. 9.1)
удовлетворяет приведенной ниже функциональной зависимости, поскольку все
кортежи отношения SCP с одинаковым значением атрибута S# имеют одинаковое
значение атрибута CITY.
На самом деле это отношение удовлетворяет нескольким функциональным
зависимостям:
(Упражнение. Проверьте правильность этого утверждения).
Левая и правая стороны символической записи функциональной зависимости
иногда называются детерминантом и зависимой частью соответственно. Как
говорится в определении, детерминант и зависимая часть являются множествами
атрибутов. Когда множество содержит только один атрибут, он называется
одноэлементным множеством, скобки опускаются и символическая запись
принимает вид
Как было замечено ранее, эти функциональные зависимости относятся к "пункту
(а)", т.е. к отдельным значениям отношения. Однако при рассмотрении переменных
отношения, например базовых отношений, интерес представляют не столько
функциональные зависимости для определенного в некоторый момент времени

значения, сколько функциональные зависимости, выполняющиеся для всех
возможных значений данной переменной. Например, в случае отношения SCP
функциональная зависимость
выполняется для всех возможных значений SCP, поскольку в любой момент
времени данному поставщику соответствует в точности один город; таким образом,
любые два кортежа отношения SCP в один и тот же момент времени и с одним и тем
же номером поставщика должны соответствовать одному и тому же городу.
Практически утверждение, что данная функциональная зависимость выполняется
"всегда" (т.е. для всех возможных значений SCP), является ограничением
целостности для отношения SCP, поскольку при этом накладываются
определенные ограничения на все допустимые значения.
Ниже приведено определение концепции функциональной зависимости для
пункта (б) (в нем расширения определения, данного для пункта (а), отмечены
полужирным шрифтом).
■ ■BBBBBBB Пусть R является переменной отношения, а X и Y— произвольными
подмножествами множества атрибутов отношения R. Тогда Y функционально
зависимо от X, что в символическом виде записывается как
(и читается либо как "X функционально определяет Y”, либо как “X стрелка Y”),
тогда и только тогда, когда для любого допустимого значения отношения R
каждое значение X связано в точности с одним значением Y.
Иначе говоря, для любого допустимого значения отношения R, когда бы два
кортежа отношения R ни совпадали по значению X, они также совпадают и по
значению Y. Следовательно, далее термин "функциональная зависимость" будет
использоваться в последнем безотносительном ко времени смысле (за исключением
особо оговоренных случаев).
Ниже перечислено несколько безотносительных ко времени функциональных
зависимостей для переменной отношения SCP:
Обратите внимание, в частности, на функциональные зависимости, которые
выполняются для таблицы на рис. 9.1, но не выполняются "всегда":
Иначе говоря, например, такое утверждение, как "число деталей для каждой
поставки данного поставщика одинаково", истинно для значений таблицы на рис.
9.1, но не верно для всех возможных допустимых значений отношения SCP.
Следует отметить, что если X является потенциальным ключом отношения R,
например X является первичным ключом, то все атрибуты Y отношения R должны
быть обязательно функционально зависимы от X (это следует из определения

потенциального ключа). В обычном отношении деталей Р, например, необходимо,
чтобы выполнялась зависимость
Фактически, если отношение R удовлетворяет функциональной зависимости А
®
В и А не является потенциальным ключом, то R будет характеризоваться некоторой
избыточностью. Например, в случае отношения SCP сведения о том, что каждый
данный поставщик находится в данном городе, будут повторяться много раз (это
хорошо видно на рис. 9.1). Более подробно этот вопрос обсуждается в главе 10.
Теперь, даже если ограничиться рассмотрением функциональных зависимостей,
которые выполняются "всегда", множество функциональных зависимостей,
выполняющихся для всех допустимых значений данного отношения может быть все
еще очень большим, как показано на примере отношения SCP. (Упражнение
попробуйте записать полное множество функциональных зависимостей для
отношения SCP;.) Большая часть оставшегося в этой главе материала посвящается
методам сокращения этого обширного множества ФЗ до компактных размеров.
Почему эта цель столь важна? Одна из причин состоит в том, что, как уже
отмечалось, функциональные зависимости являются ограничениями целостности,
поэтому при каждом обновлении данных в СУБД все они должны быть проверены.
Следовательно, для заданного множества функциональных зависимостей 5
желательно найти такое множество Т, которое (в идеальной ситуации) было бы
гораздо меньшего размера, чем множество S, причем каждая ФЗ множества S могла
бы быть заменена функциональной зависимостью множества Т. Если бы такое
множество Т было найдено, то в СУБД достаточно было бы использовать ФЗ из
множества Т, а ФЗ из множества 5 подразумевались бы автоматически. Поэтому
задача поиска подходящего множества Т представляет большой практический
интерес.
17. 9.3. Тривиальные и нетривиальные зависимости
Замечание. Далее в этой главе выражение "функциональная зависимость" будет
иногда для краткости заменяться словом "зависимость", а "функционально зависим
от — словами "функционально определяется как" и т.п.
Очевидным способом сокращения размера множества ФЗ было бы исключение
тривиальных зависимостей, т.е. таких, которые не могут не выполняться. В качестве
примера приведем тривиальную ФЗ для отношения SCP из предыдущего раздела:
Фактически ФЗ тривиальна тогда и только тогда, когда правая часть
символической записи данной зависимости является подмножеством (не
обязательно собственным подмножеством) левой части.
Как следует из названия, такие зависимости не представляют никакого интереса
с практической точки зрения, в отличие от нетривиальных зависимостей, которые
фактически являются "истинными" ограничениями целостности. Однако в
формальной теории зависимостей не следует предполагать присутствие только
нетривиальных зависимостей.

18. 9.4. Замыкание множества зависимостей
Как уже упоминалось выше, некоторые ФЗ могут означать другие ФЗ.
Например, приведенная ниже зависимость
подразумевает следующие ФЗ:
В качестве более сложного примера можно привести отношение R с тремя
атрибутами А, В и С, для которых выполняются функциональные зависимости А®В
и В®С. В таком случае нетрудно заметить, что также выполняется зависимость
А®С, которая называется . транзитивной функциональной зависимостью, т.е. С
транзитивно через В зависит от А.
Множество всех ФЗ, которые задаются данным множеством функциональных
зависимостей 5, называется замыканием S и обозначается символом S
+
. Из
сказанного выше становится ясно, что для выполнения сформулированной задачи
следует найти способ вычисления S
+
на основе S. Первой попыткой решить эту
проблему была статья Армстронга (Armstrong) [9.1], в которой представлен набор
правил вывода функциональных зависимостей на основе заданных (эти правила
также называются аксиомами Армстронга). Правила могут формулироваться
разными способами, а самый простой из них приводится ниже.
■ ■BBBBBBB Правила вывода Армстронга. Пусть в перечисленных ниже правилах А, В
и С — произвольные подмножества множества атрибутов заданного отношения
R, а символическая запись АВ означает объединение А и В.
1. 1.BBBBBB Рефлексивность: если В является подмножеством А, А®В.
2. 2.BBBBBB Дополнение: если А®В, то АС®ВС.
3. 3.BBBBBB Транзитивность: если А®В и В®С, то А®С
Каждое из этих правил может быть непосредственно доказано на основе
определения функциональной зависимости (первое из них — это всего лишь
определение тривиальной зависимости). Более того, эти правила являются
полными в том смысле, что для заданного множества функциональных
зависимостей S минимальный набор ФЗ, которые подразумевают все зависимости S,
может быть выведен из S на основе этих правил. Они также являются
исчерпывающими, поскольку никакие дополнительные ФЗ не могут быть
выведены (т.е. ФЗ, которые не подразумеваются зависимостями множества S).
Иначе говоря, эти правила могут быть использованы для получения замыкания S
+
.
Из трех описанных выше правил для упрощения задачи практического
вычисления замыкания S
+
можно вывести несколько других правил. (Пусть D — это
другое произвольное подмножество множества атрибутов R.)
4. 4.BBBBBB Самоопределение: А®А.
5. 5.BBBBBB Деклмпозиция: если А®ВС, то А®В и A®С.
6. 6.BBBBBB Объединение: если А®В и А®С, А®ВС.
7. 7.BBBBBB Композиция: если А®В и С®D, то АС®ВD.
Кроме того, Дарвен (Darwen) в своей работе [9.6] доказал следующее правило,
которое назвал теоремой всеобщего объединения:
8. 8.BBBBBB Если А®В и С®D, то
BDBCA ®
(где символ “
” обозначает

объединение множеств, а символ “–” — их разность).
Название “теорема всеобщего объединения” указывает на то, что некоторые
перечисленные ранее правила могут быть выведены как частные случаи этой
теоремы [9.6].
Пример. Пусть дано некоторое отношение R с атрибутами А, В, С, D, E, F и
следующими ФЗ:
Обратите внимание, что способ записи несколько изменился (без ущерба для
смысла): например, символы ВС означают множество, состоящее из атрибутов В и
С, хотя ранее эти символы означали объединение В и С, где В и С были
множествами атрибутов.
Замечание. Если необходимо, этому примеру можно придать более конкретный
смысл, а именно: А — номер сотрудника, В — номер отдела, С — номер
руководителя (начальника) данного сотрудника, D — номер проекта, возглавляемого
данным руководителем (уникальный для каждого отдельно взятого руководителя),
Е — название отдела, F — доля времени, уделяемая данным руководителем
заданному проекту.
Теперь можно показать, что зависимость AD
®
F выполняется для отношения R и
таким образом принадлежит замыканию данного множества ФЗ.
19. 9.5. Замыкание множества атрибутов
Хотя в предыдущем разделе так и не был дан эффективный алгоритм для
вычисления замыкания S
+
на основе множества функциональных зависимостей S, в
этом разделе описан алгоритм определения, будет ли данная ФЗ находиться в
данном замыкании. Для этого прежде всего следует дать определение понятию
суперключ. Суперключ отношения R — это множество атрибутов отношения R,
которое содержит в виде подмножества, но не обязательно собственного
подмножества, по крайней мере один потенциальный ключ. (Определение термина
"суперключ", таким образом, может быть выведено из определения понятия
"потенциальный ключ".) Таким образом, отсюда следует, что суперключи для
данного отношения R — это такие подмножества К множества атрибутов отношения
R, что функциональная зависимость
истинна для каждого атрибута А отношения R.
Теперь предположим, что известны некоторые ФЗ, выполняющиеся для данного
отношения, и требуется определить потенциальные ключи этого отношения. По
определению потенциальными ключами называются неприводимые суперключи

(т.е. суперключ содержит потенциальный ключ). Таким образом, выясняя, является
ли данное множество атрибутов К суперключом, можно в значительной степени
продвинуться к выяснению вопроса, является ли К потенциальным ключом.
Для этого нужно определить, будет ли набор атрибутов отношения R
множеством всех атрибутов, функционально зависящих от К. Таким образом, для
заданного множества зависимостей S, которые выполняются для отношения R,
необходимо найти способ определения множества всех атрибутов отношения R,
которые функционально зависимы от К, т.е. так называемое замыкание K
+
множества К для S. Простой алгоритм вычисления этого замыкания показан на рис.
9.2. Ниже даны пояснения. Упражнение. Докажите, что этот алгоритм правильный.
Пример. Предположим, что дано отношение R с атрибутами А, В, С, D, E и F и
следующими ФЗ:
Теперь вычислим замыкание {А, В}
+
множества атрибутов {А, В} для данного
множества ФЗ.
1. 1.BBBBBB Присвоим замыканию CLOSURE, S начальное значение — множество {А,
В}.
2. 2.BBBBBB Теперь выполним внутренний цикл четыре раза, по одному разу для каждой
ФЗ. На первой итерации (для зависимости А ® ВС) будет обнаружено, что левая
часть действительно является подмножеством замыкания CLOSURE[K, S];
таким образом, к результату можно добавить атрибуты В и С. Замыкание
CLOSURE[K, S] теперь представляет собой множество {А, В, С}.
3. 3.BBBBBB На второй итерации (для зависимости Е
®
CF) можно обнаружить, что левая
часть не является подмножеством полученного до этого момента результата;
который, таким образом, остается неизменным.
4. 4.BBBBBB На третьей итерации (для зависимости В
®
Е) множество Е будет добавлено
к замыканию CLOSURE[K, S], которое теперь будет иметь вид {А, В, С, Е}.
5. 5.BBBBBB На четвертой итерации (для зависимости CD
®
EF) замыкание CLOSURE[K,
S] останется неизменным.
6. 6.BBBBBB Теперь внутренний цикл будет выполнен еще четыре раза. На первой
итерации результат останется прежним, на второй он будет расширен до {А, В,
С, Е, F}, а на третьей и четвертой — снова не изменится.

7. Наконец, после еще одного четырехкратного прохождения цикла замыкание
CLOSURE[K, S] остается неизменным и весь процесс в целом завершается с
результатом {А, В, С, Е, F}
+
={A, В, С, Е, F}. Обратите внимание, что {А, В} не
является суперключом (и, следовательно, потенциальным ключом).
Из сказанного выше можно сделать очень важное заключение: для заданного
множества функциональных зависимостей S можно легко указать, будет ли заданная
зависимость А®Y следовать из S, поскольку это возможно тогда и только тогда,
когда Y является подмножеством замыкания X
+
множества X для заданного
множества S. Иначе говоря, таким образом представлен простой способ
определения, будет ли данная функциональная зависимость X®Y включена в
замыкание S
+
множества S.
20. 9.6. Неприводимое множество зависимостей
Пусть S1 и S2 являются двумя множествами ФЗ. Если любая ФЗ, которая
является зависимостью множества S1, также является зависимостью множества S2,
т.е. если S1
+
является подмножеством S2
+
, то S2 называется покрытием для S1.
(Некоторые авторы используют термин "покрытие" для обозначения
эквивалентного множества.) Это значит, что если накладываемые в СУБД
ограничения представлены зависимостями множества S2, то в этой СУБД также
наложены ограничения на основе зависимостей множества S1.
Далее, если S2 является покрытием для S1, а S1 — покрытием для S2, т.е. если
S1
+
=S2
+
, то S1 и S2 эквивалентны. Ясно, что если S1 и S2 эквивалентны и
наложенные в СУБД ограничения представлены зависимостями множества S2, то
эти ограничения также могут быть представлены зависимостями множества S1,
верно также и обратное утверждение.
Множество ФЗ называется неприводимым тогда и только тогда, когда
выполняются перечисленные ниже свойства.
1. 1.BBBBBB Правая часть (зависимая часть) каждой ФЗ множества S содержит только
один атрибут (т.е. является одноэлементным множеством).
2. 2.BBBBBB Левая часть (детерминант) каждой ФЗ множества S является неприводимой,
т.е. ни один атрибут не может быть опущен из детерминанта без изменения
замыкания S
+
(без конвертирования множества S в некоторое множество, не
эквивалентное множеству S). В таком случае ФЗ является неприводимой слева.
3. 3.BBBBBB Ни одна функциональная зависимость в S не может быть опущена из S без
изменения замыкания S
+
(т.е. без конвертирования множества S в некоторое
множество, не эквивалентное множеству S).
В качестве примера рассмотрим уже знакомое отношение деталей Р с
перечисленными ФЗ:
Нетрудно заметить, что этот набор ФЗ является неприводимым: правая часть
каждой зависимости содержит только один атрибут, левая часть, очевидно, является
неприводимой, кроме того, ни одна из перечисленных ФЗ не может быть опущена
