Дейт К. Введение в системы баз данных
Подождите немного. Документ загружается.


рассматривается достаточно общий случай. Дело в том, что оригинальное
определение Кодда для ЗНФ [9.4] не совсем подходит для отношений с
перечисленными ниже условиями.
1. 1.BBBBBB Отношение имеет два (или более) потенциальных ключа.
2. 2.BBBBBB Два потенциальных ключа являются сложными.
3. 3.BBBBBB Они перекрываются (т.е. имеют, по крайней мере, один общий атрибут).
Поэтому оригинальное определение ЗНФ было впоследствии заменено более
строгим определением Бойса-Кодда (Boyce/Codd) [10.2], для которого было принято
отдельное название — нормальная форма Бойса-Кодда, НФБК. (На самом деле
строгое определение "третьей" нормальной формы, эквивалентное определению
нормальной формы Бойса-Кодда, было впервые дано Хезом (Heath) в 1971 году
[10.4], и этой форме следовало бы дать название "нормальная форма Хеза".)
Замечание. Комбинация условий 1, 2 и 3 не часто встречается на практике, и
для отношения без этих условий ЗНФ и НФБК эквивалентны.
Для объяснения понятия НФБК потребуется использовать понятие
детерминанта, введенное в главе 9 для левой части ФЗ, а также тривиальной
функциональной зависимости, т.е. ФЗ, в которой левая часть является
супермножеством правой части.
■ ■BBBBBBB Отношение находится в нормальной форме Бойса-Кодда тогда и только
тогда, когда каждая нетривиальная и неприводимая слева ФЗ обладает
потенциальным ключом в качестве детерминанта. Менее формальное
определение имеет другую формулировку.
■ ■BBBBBBB Отношение находится в нормальной форме Бойса-Кодда тогда и только
тогда, когда детерминанты являются потенциальными ключами.
Иначе говоря, на диаграмме ФЗ стрелки будут начинаться только с
потенциальных ключей. Согласно данному определению никакие другие стрелки не
допускаются и, следовательно, никакие стрелки не могут быть исключены с
помощью процедуры нормализации.
Замечание. Выражаясь более кратко и неформально, различие между двумя
определениями НФБК заключается в том, что детерминанты "не очень велики" и все
ФЗ нетривиальны. Для простоты изложения далее в этой главе будут использованы
точно такие же допущения, за исключением особо оговоренных случаев.
Стоит отметить также, что определение НФБК концептуально проще, чем
прежнее определение ЗНФ, поскольку в нем нет явных ссылок на первую и вторую
нормальную форму, а также не используется концепция транзитивной зависимости.
Кроме того, хотя (как уже отмечалось выше) определение НФБК является более
строгим, чем определение ЗНФ, все же любое определенное отношение может быть
подвергнуто декомпозиции без потерь информации в эквивалентный набор
отношений в НФБК.
Прежде чем рассматривать примеры отношений с несколькими
потенциальными ключами, убедимся, что отношения FIRST и SECOND, которые не
находятся в ЗНФ, также не находятся и в НФБК. А также убедимся, что отношения
SP, SC и CS, которые находятся в ЗНФ, находятся и в НФБК. Отношение FIRST
содержит три детерминанта, а именно: S#, CITY и {S#, P#}, из которых только {S#,
P#} является потенциальным ключом. Поэтому отношение FIRST не находится в
НФБК. Аналогичное утверждение верно для отношения SECOND, поскольку
детерминант CITY не является потенциальным ключом. Отношения SP, SC и CS, с
другой стороны, находятся в НФБК, поскольку в каждом случае единственный
потенциальный ключ является единственным детерминантом в этом отношении.
Теперь следует рассмотреть пример, включающий два неперекрывающихся
потенциальных ключа. Допустим, что в отношении поставщиков
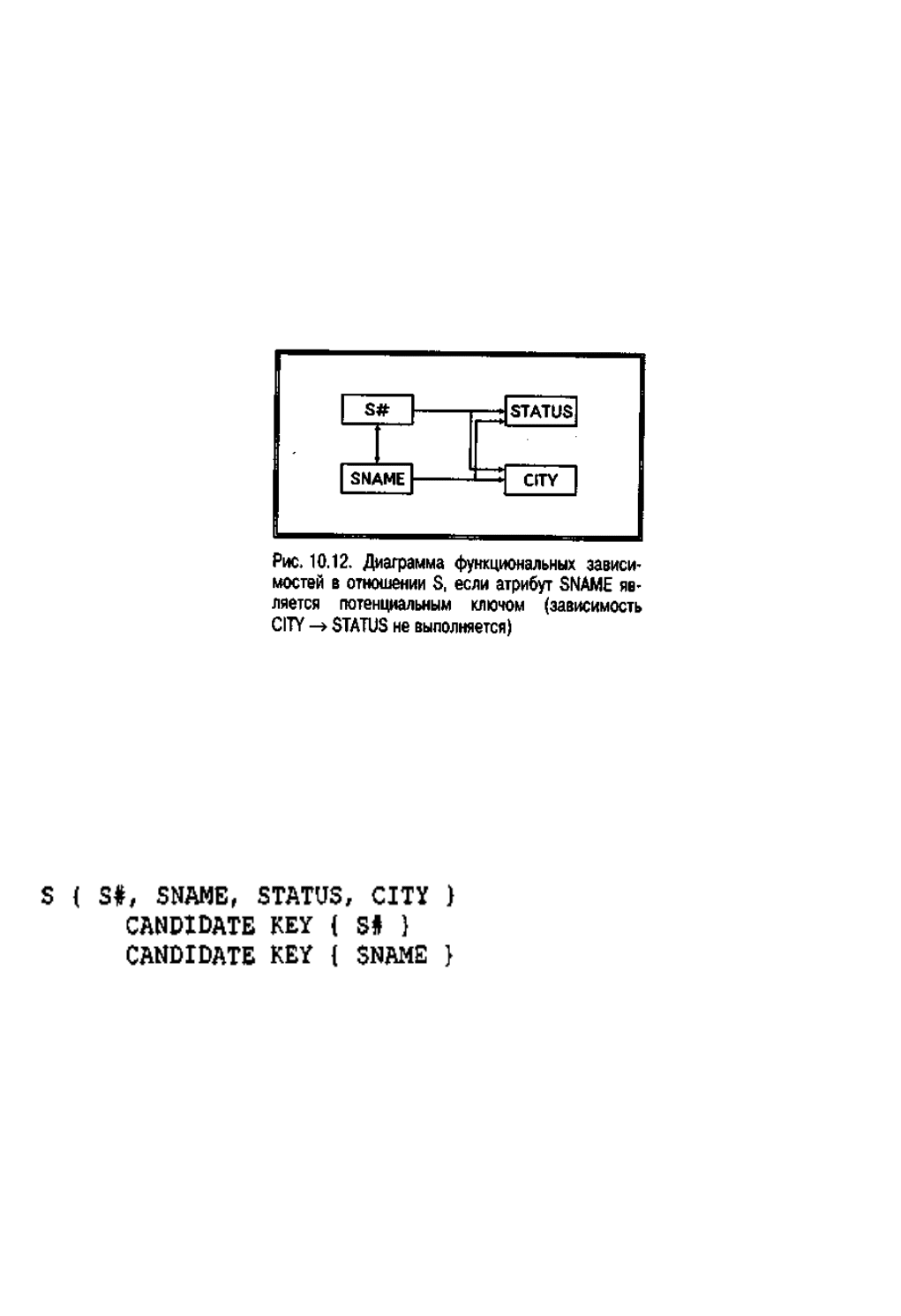
S { S#, SNAME, STATUS, CITY }
атрибуты S# и SNAME являются потенциальными ключами (т.е. в этом случае
каждый поставщик имеет уникальный номер и уникальное имя). Предположим,
однако (как, впрочем, всюду в этой книге), что атрибуты STATUS и CITY
совершенно независимы, т.е. введенная специально для частных целей предыдущих
разделов функциональная зависимость CITY®STATUS больше не выполняется. В
этом случае диаграмма ФЗ будет иметь вид, показанный на рис. 10.12.
Это отношение S находится в НФБК. Хотя данная диаграмма существенно
"сложнее" диаграммы зависимостей для отношения в ЗНФ, тем не менее, в этом
случае все детерминанты являются потенциальными ключами, а все стрелки
начинаются с потенциальных ключей. Таким образом, иметь несколько
потенциальных ключей не так уж и плохо. Однако желательно, чтобы атрибут
SNAME был представлен как потенциальный ключ еще при определении базы
данных, чтобы в СУБД было задействовано требуемое ограничение уникальности.
После реализации всех перечисленных условий отношение S будет выглядеть так:
Теперь нужно представить несколько примеров, в которых потенциальные
ключи перекрываются. Это происходит, если они содержат по два или более
атрибута и имеют, по крайней мере, один общий атрибут. (В соответствии с
доводами, которые приводились в главе 5, в примерах этой главы не будет
выбираться первичный ключ из имеющихся потенциальных. Поэтому далее в
таблицах никакие колонки не будут выделяться с помощью двойной линии.) В
первом примере рассмотрим отношение, в котором допустимо, что имена
поставщиков уникальны:
SSP { S#, SNAME, P#, QTY }
Потенциальными ключами в нем являются {S#, P#} и {SNAME, Р#}. Однако
это отношение не находится в НФБК, так как содержит два детерминанта, S# и
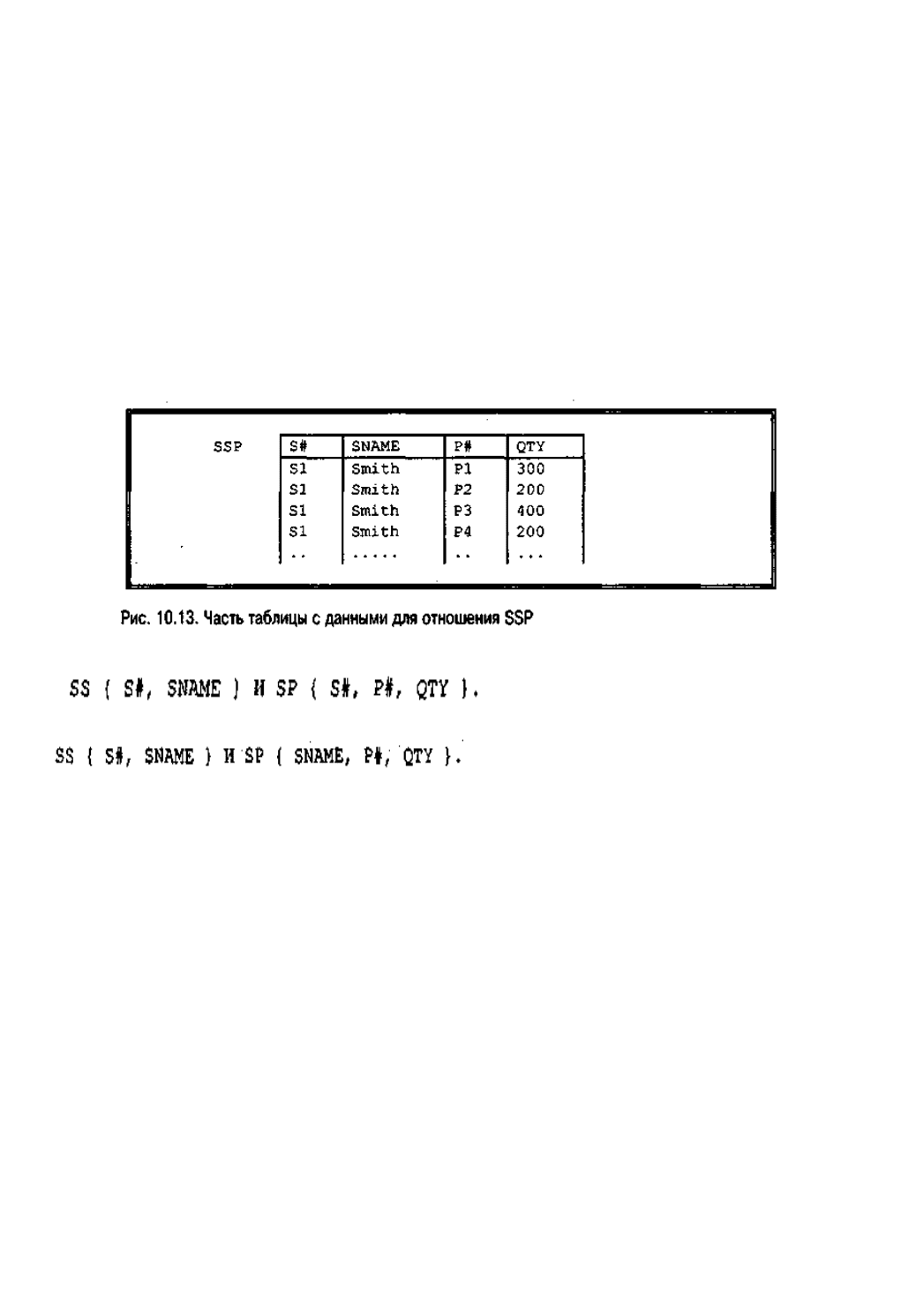
SNAME, которые не являются потенциальными ключами этого отношения (S# и
SNAME — детерминанты, поскольку они определяют друг друга). Некоторые
значения этого отношения SSP показаны на рис. 10.13. Как видно из этого рисунка,
в отношении SSP содержится некоторая доля избыточности, присущая отношениям
SCP, FIRST и SECOND из предыдущих разделов этой главы, поэтому оно
характеризуется такими же аномалиями обновления. Например, изменение имени
поставщика S1 точно так же приведет либо к выполнению поиска, либо к
получению несовместимых результатов. К тому же, отношение SSP находится в
3НФ, поскольку согласно старому определению не требуется, чтобы атрибут был
неприводимо зависим от каждого потенциального ключа, если он сам является
компонентом некоторого потенциального ключа данного отношения. Таким
образом, тот факт, что атрибут SNAME приводимо зависим от {S#, P#},
игнорируется. (Под термином "3НФ" здесь подразумевается определение, данное
Коддом в [9.4], а не упрощенное определение, данное выше в этой главе.)
Для решения проблемы отношение SSP следует разбить на две проекции:
Однако для разбиения можно выбрать также альтернативные проекции
Обратите внимание, что в данном примере возможно существование двух в
одинаковой мере допустимых декомпозиций, причем все их проекции находятся в
НФБК.
Здесь следует сделать небольшое отступление и пояснить, что же "в
действительности" происходит. Вероятно, что исходный макет, состоящий на
одного отношения SSP, неудачен, а возникающие в связи с этим проблемы —
очевидны. Маловероятно, чтобы опытный разработчик баз данных предложил такой
макет, даже если он совсем не знаком с концепцией НФБК (и т.д.). Исходя из
здравого смысла, макет на основе отношений SS-SP, несомненно, лучше. Однако,
что подразумевается под "здравым смыслом" и в соответствии с какими принципами
разработчику следует отдать предпочтение макету типа SS-SP вместо макета типа
SSP.
Конечно, для этого используются принципы функциональной зависимости и
нормальной формы Бойса-Кодда. Иначе говоря, эти концепции (ФЗ, НФБК и всех
других формальных идей, изложенных в этой и следующей главе) являются не более
и не менее, как соображениями здравого смысла, записанными в формальном виде.
Основной идеей излагаемой здесь теории является поиск и формулирование этих
принципов здравого смысла, что, конечно же, весьма непростая задача. Однако если
такая задача может быть выполнена, то такие принципы могут быть
автоматизированы, т.е. можно написать программу для выполнения ее с помощью
компьютера. Критики метода нормализации обычно упускают этот момент из виду,
поскольку совершенно справедливо заявляют, что эти идеи в основном
представляют собой всего лишь соображения здравого смысла. Однако при этом не
принимается во внимание, что возможность формальной и строгой формулировки
"соображений здравого смысла" сама по себе уже является значительным
достижением.
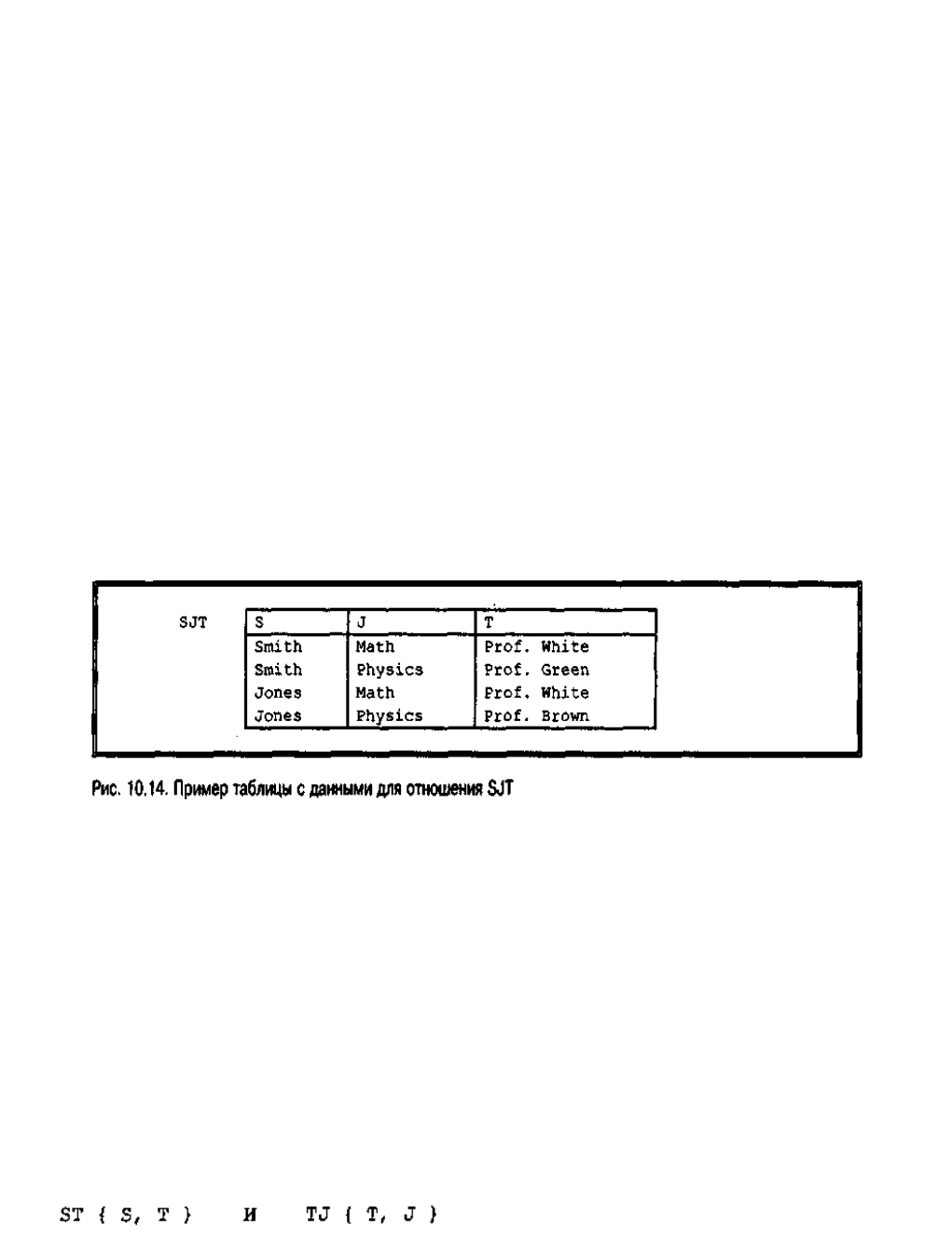
Теперь вернемся к основной теме данного раздела и рассмотрим второй пример
с перекрывающимися потенциальными ключами на основе отношения SJT с
атрибутами S, J и Т, которые обозначают студента, предмет и преподавателя
соответственно (следует предупредить, что это всего лишь пример, к тому же
достаточно экзотический). Кортеж {S:s, J:j, Т:t} отношения SJT означает, что
некоторый студент s обучается некоторому предмету y некоторым преподавателем t.
При этом накладываются перечисленные ниже ограничения.
■ ■BBBBBBB Каждый студент, изучающий данный предмет, обучается только одним
преподавателем.
■ ■BBBBBBB Каждый преподаватель ведет только один предмет (но каждый предмет
может преподаваться несколькими преподавателями).
На рис. 10.14 показан пример таблицы этого отношения.
Какие функциональные зависимости существуют в данном отношении?
Из первого ограничения следует зависимость атрибута Т от комбинации
атрибутов {S, J}, а из второго — зависимость атрибута J от атрибута Т.
Следовательно, диаграмма ФЗ будет иметь вид, показанный на рис. 10.15.
Опять в рассматриваемом примере есть два перекрывающихся потенциальных
ключа, а именно: комбинация {S, J} и комбинация {S, Т}. Снова отношение
находится в 3НФ, а не в НФБК и характеризуется некоторыми аномалиями
обновления. Например, если требуется удалить информацию о том, что Джонс
(Jones) изучает физику, это нельзя будет сделать, не утрачивая информацию о том,
что профессор Браун (Prof. Brown) преподает физику. Эти трудности вызваны тем,
что Т является детерминантом, но не является потенциальным ключом. Опять для
решения этой проблемы исходное отношение следует разбить на две проекции,
которые находятся в НФБК:

Читателю предлагается в качестве упражнения составить таблицы данных для
этих двух отношений, соответствующие данным из таблицы на рис. 10.14,
нарисовать соответствующую диаграмму ФЗ для проверки того, что эти две
проекции в действительности находятся в НФБК (какие атрибуты являются
потенциальными ключами?), а также убедиться, что эта декомпозиция позволяет
устранить все проблемы.
Нельзя не отметить тот факт, что, несмотря на разрешение некоторых проблем
с помощью такой декомпозиции, к сожалению, она характеризуется другими
трудностями. Дело в том, что две проекции, ST и TJ, не являются независимыми в
смысле Риссанена (подробнее это обсуждалось выше в данной главе). Точнее
говоря, Ф3
не может быть выведена из единственной ФЗ, которая присутствует в двух данных
проекциях,
В результате эти две проекции не могут быть обновлены независимо.
Например, попытка вставить в отношение ST кортеж для Смита (Smith) и
профессора Брауна (Prof. Brown) должна быть отвергнута, поскольку профессор
Браун преподает физику, а Смит уже обучается физике у профессора Грина (Prof.
Green). Однако обнаружить этот факт без проверки отношения TJ система не может.
Таким образом, можно прийти к неприятному выводу, что две цели, а именно:
декомпозиция отношения на отношения, находящиеся в НФБК, и декомпозиция на
независимые компоненты, могут привести к конфликтной ситуации. Поэтому не
всегда возможно удовлетворять обеим целям одновременно.
Замечание. В действительности отношение SJT является атомарным
(атомарные отношения обсуждались выше в этой главе), даже если оно не находится
в НФБК. Однако то, что атомарное отношение не может быть подвергнуто
декомпозиции на независимые компоненты, не означает, что оно не может быть
подвергнуто декомпозиции вовсе (где "декомпозиция" означает декомпозицию без
потерь). "Атомарное отношение" — не совсем подходящий термин для этой
концепции, по крайней мере с интуитивной точки зрения, так как такая, атомарность
не является ни необходимым, ни достаточным условием создания хорошего макета
базы данных.
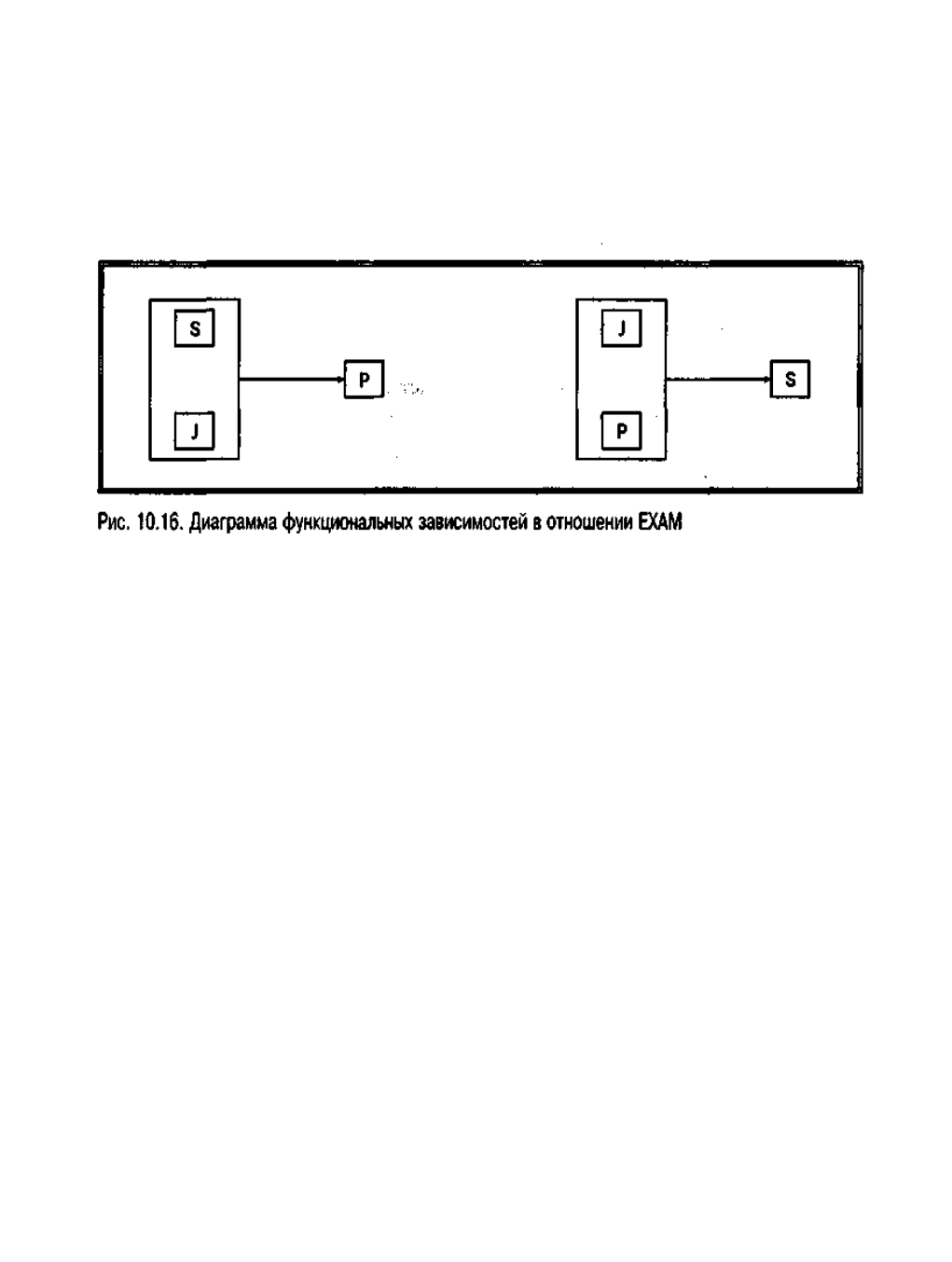
В третьем, и последнем, примере отношения с перекрывающимися
потенциальными ключами рассмотрим отношение EXAM с атрибутами S (студент),
J (предмет) и Р (место). Смысл кортежа {S:s, J:j, Р:р} отношения EXAM заключается
в том, что некоторый студент s экзаменуется по определенному предмету j и
занимает определенное место р в списке. Допустим также следующее ограничение:
■ ■BBBBBBB никакие два студента не могут занять одно и то же место в списке по одному
и тому же предмету.
В таком случае диаграмма ФЗ будет такой, как на рис. 10.16.
В этом примере опять появляются два перекрывающихся потенциальных ключа
— {S, J} и {J, Р}, поскольку для данного студента и предмета существует точно
одно соответствующее им место в списке, а также для данного предмета и места в
списке существует точно один соответствующий им студент. Однако такое
отношение находится в НФБК, поскольку эти потенциальные ключи являются
единственными детерминантами. Читатель может убедиться, что данное отношение
не характеризуется аномалиями обновления, подобными упомянутым ранее в этой
главе. Таким образом, наличие перекрывающихся потенциальных ключей не всегда
приводит к возникновению проблем такого рода.
В заключение следует подчеркнуть, что концепция НФБК позволяет избавиться
от некоторых проблем, присущих, по крайней мере теоретически, формам,
соответствующим старому определению ЗНФ. Более того, новое определение
концептуально проще старого, так как в нем не используются понятия 1НФ, 2НФ,
первичного ключа или транзитивной зависимости. Кроме того, понятие
потенциального ключа может быть заменено введением более фундаментального
понятия функциональной зависимости (в определении, данном в [10.2], фактически
сделана такая замена). С другой стороны, концепции первичного ключа,
транзитивной зависимости и т.д. весьма полезны на практике, поскольку позволяют
представить идею постепенного процесса, выполняемого разработчиком для
приведения произвольного отношения к эквивалентному набору отношений в
НФБК.
Наконец, заметим, что в ответах на упражнения в конце этой главы содержится
алгоритм, согласно которому произвольное отношение может быть подвергнуто
декомпозиции без потерь информации в набор проекций, находящихся в НФБК.
