Давнис В.В. Прогнозные модели экспертных предпочтений

Подождите немного. Документ загружается.

Окончание табл. 3.12

Курский

Курчатовский

Льговский

Мантуровский

Фатежский

Хомутовский

Черемисиновский

Щигровский

Сравнение табл. 3.11 и 3.12 позволяет сделать вывод о том,

что результаты моделирования с использованием построенной

модели и экспертные оценки, в основном, совпадают. В целом,

Курская область действительно малопривлекательна. Однако по

ряду районов (Горшеченскому, Рыльскому, Суджанскому, Фатеж-

скому) имеются расхождения во мнениях. Это может свидетель-

ствовать о том, что эксперты располагают дополнительной инфор-

мацией о тенденциях, которые пока еше не нашли отражение в

официальной статистике, но проявление которых ожидается в

ближайшем будущем.

В подобных ситуациях следует рекомендовать корректирующие

уточнения базовой модели (*) с учетом субъективных мнений

экспертов. Возможны различные варианты подобного уточнения.

Предлагаемая нами методика позволяет это делать.

3.5.

Модели множественного выбора

в экспертном оценивании будущего

3.5.1.

Мультиномиальная логит-модель

множественного выбора

Рассмотрим случай, когда перед экспертами стоит

задача выбора не среди двух, а среди целого множества альтер-

нативных вариантов. По результатам их выбора, оформленным в

виде псевдовыборки, требуется построить модель, с помощью

которой можно будет осуществлять прогнозные расчеты эксперт-

ных предпочтений в виде соответствующих вероятностей. Для

решения этой задачи можно воспользоваться мультиномиальной

логит-моделью, которая по сути является обобщением логит-мо-

дели бинарного выбора. Ниже достаточно подробно описывается

мультиномиальная логит-модель и некоторые детали, характери-

зующие особенность ее построения и анализа.

Предварительно все варианты множественного выбора нумеру-

ются в произвольном порядке: 0, 1, 2, ..., /. (Нумерация начата

100

только

для

того, чтобы было единообразие

предыдущей

кодировкой

0 и 1.)

Вероятность наступления того

или

иного

ва-

рианта описывается полиномиальной логит-моделью

Р(>',=7')

= ^ '

0,1,2,...,/. (3.100)

Вектор независимых переменных

(

. = [г

;

]

составлен

из

двух

подвекторов, каждый

из

которых имеет собственную смысловую

нагрузку. Компоненты вектора

принято называть атрибутами

понимать

их как

показатели,

по

которым различаются альтерна-

тивы.

свою очередь, компоненты вектора

(

называют харак-

теристиками, понимая

под

ними описание индивидуальных черт

тех

лиц,

которые осуществляли выбор альтернатив.

Оценка параметров модели (3.100)

не

дает однозначного

ре-

зультата,

так как

вместе

вычисленными коэффициентами

идентичные вероятности позволяют получить вектор

Избе-

жать этой неоднозначности позволяет операция нормализации

(стандартизации), смысл которой

в том,

чтобы

для

одного

из ва-

риантов, например

= /,

положить

= 0.

Тогда оценивается

не

/ + 1

функция,

a /

функций одного вида

Р(У,-

У')

—1=1

7 =

1,2,...,./,

(3.101)

1+1У'

после чего определяется

еще

одна функция через значения этих

функций путем вычитания

их

суммы

из

единицы:

1+2У" (3.102)

7=0

Это одна

из

особенностей построения полиномиальной логит-

модели.

соответствии

этой особенностью компьютерные

па-

кеты рассчитывают только коэффициенты первых

зависимостей

, b,,...,

по

которым вычисляются

соответствии

(3.101)

первые /вероятностей Р(у,

= 0), Р(у

(

. =

1),...

, PCv, = /

—

1). Ве-

роятность выбора последнего варианта Р(у-

= J)

компьютером

не

рассчитывается,

определяется отдельно

помощью (3.102).

101

Форма логит-модели, применяемой для бинарного выбора, опи-

сание которой приведено выше, легко получается из полиномиаль-

ной при J = 2. В силу того, что логит-модель является частным

случаем полиномиальной, ее часто называют биномиальной.

Оценивание коэффициентов модели осуществляется путем чис-

ленного решения уравнений правдоподобия. Для записи самого

уравнения правдоподобия, а точнее его логарифмической формы,

удобно ввести переменную */.., которая принимает значение 1,

если в /-м наблюдении (z'-м индивидуумом) был выбран у'-й аль-

тернативный вариант среди (/ + 1)-го, и 0 — в противном слу-

чае.

Тогда для каждого /' только одно из

й--

будет равно 1.

Используя введенную переменную dp запишем функцию лога-

рифмического правдоподобия

1пь=££^1п

(=1 у=0

Xybi.

е '

(3.103)

Дифференцируя это выражение по b, получим систему уравне-

ний максимального правдоподобия

—-it'.—'»

{ \

0 ' -I

к=0

1=1 ;=0

к=0

х,Ь,

х,=

•54

1=1

х,Ь,

е '

2у,ь<

к=0 )

*; =£[<*,,-РуК=0,

=0,1,2,.../-!. (3.104)

102

Заметим, что ву'-м блоке уравнений суммирование идет по всем

/, причем если в /-м случае был выбран у'-й вариант, т.е. y-

= j,

то в квадратных скобках имеем [1

—

Р^], в противном случае

[—

Р.].

Решение этой системы с учетом того, что Ь

= 0, осуществ-

ляется численно с помощью метода Ньютона — Рафсона. Ком-

пьютерная реализация устроена таким образом, и об этом уже го-

ворилось, что нулевые значения получают параметры той модели,

которая соответствует последней из указанных альтернатив. Дру-

гими словами, если бы мы захотели, чтобы Ь

= 0, а не Ь

, то

данные, соответствующие альтернативе с номером у ~ О, долж-

ны быть введены последними.

Для реализации метода Ньютона — Рафсона требуется матрица

частных производных второго порядка. Кроме того, с помощью

этой матрицы определяются характеристики надежности самой

модели. Поэтому имеет смысл выписать эту матрицу в общем виде:

1пЬ Э "

х,Ь,

,Ь,

к=0

;

/=1

к=0

x,b,

V" x,b

х b x,b,

е ' ' Xi

e e ' '

х,.

х,.=

=-1

1=1

ЗУ

*=0

х.Ь,

1(7=0--

x,bj

5У"

(t=0 )

х,х,.=

=-ik№j=i)-P«)h'x, (3.105)

В полученном выражении 1(/ = I) принимает значение 1 при

у = / и 0 — в противном случае. Это позволяет осуществлять

селекцию, так как результатом произведения РЛ(/ = /) является Р...

103

Матрица состоит из ^-блоков, каждый из которых имеет раз-

мер по числу оцениваемых параметров, т.е. (т + 1) х (т + 1),

где т — число объясняющих переменных. Данные объясняющих

переменных должны обеспечивать обратимость этой матрицы.

Практически нет строгих ограничений на количество оценива-

емых альтернатив, однако следует помнить, что каждая новая

альтернатива требует дополнительного введения в модель т + 1

параметров.

Коэффициенты модели трудно интерпретируемы. Нелинейный

характер не позволяет непосредственно через коэффициенты про-

следить связь между уровнем вероятности и атрибутами (фактора-

ми).

Поэтому естественно для этих целей использовать предель-

ный анализ. Дифференцируя по /-му атрибуту в /-й точке у'-ю

вероятность, получаем предельный эффект в виде

dxj

дх/

/А

УГ

/Ь/

_к=0

х,Ь

( J .Л

1>"

Ъ,-е^(е

"Ь

10+

е^Ь

)

к=0 )

х,Ь,

• '

х,Ь,

х, Ь,

X:b„

x,b,

-b

ю j

x,b,

\п хЪ,

k=0 k=0

x,b,

\+-

—

k=0

x,b.

=Рцк-ь

]

(3.106)

При расчетах по этой формуле нужно помнить, что вектор Ь

в соответствии с принятым соглашением нулевой, и поэтому

первое слагаемое при определении математического ожидания

коэффициента равно нулю.

104

Таким образом, предельный эффект, получаемый при измене-

нии /-го атрибута (1-й независимой переменной) представляет

собой произведение вероятности P(y

= J) на разность коэффици-

ента, стоящего перед 1-й переменной и средней величиной это-

го коэффициента.

Предельный эффект зависит от атрибута, причем механизм этой

зависимости реализуется через вероятность и через среднюю вели-

чину коэффициента, при определении которой задействована та же

самая вероятность. При высокой вероятности так же, как и при

малой, предельный эффект незначительный. Это объясняется тем,

что при больших Р.. в средней величине коэффициента Ь, доми-

нирует величина

Ьц

и разность между ними близка к нулю. При

малых значениях Р.. разность большая, но значение самой вероят-

ности близко к нулю, а следовательно, и величина предельного

эффекта небольшая. Обобщая, можно утверждать, что 8

-> 0 в

двух случаях: когда Р.. -> 0 и когда Р..

—>

1. Своего максимально-

го значения он достигает тогда, когда вероятность близка к 0,5,

т.е.

имеет место ситуация с самым большим уровнем неопределен-

ности при выборе /-го варианта. Это естественно, так как имен-

но в этой ситуации наиболее ценна любая информация, уточня-

ющая наше представление о выборе альтернатив.

Фактически предельный эффект является функцией, с помо-

щью которой можно ранжировать атрибуты по степени их влия-

ния на выбор конкретного варианта. Кроме того, для каждого

атрибута с помощью предельного эффекта можно определить тот

вариант, на выбор которого изменение данного атрибута влияет

сильнее всего. Безусловно, подобный анализ интересен, однако

он не дает прямого ответа на главный вопрос: "Как изменится

неопределенность выбора при изменении атрибута?" Ответ можно

получить, если использовать энтропийный показатель для оценки

уровня неопределенности ситуации множественного выбора.

Обычно интерес вызывает анализ конкретной ситуации. Пусть

это ситуация с номером /. Тогда неопределенность выбора в /-и

ситуации можно определить с помощью выражения

Hi =-l fy logzVy. (3.107)

j=0

Если вероятность изменяется на величину предельного эффекта д

то,

естественно, изменяется и величина энтропийного показателя

+AH

-i(P

j)\og

j+S

(

з.108)

у=о

105

При AH

< 0 увеличение соответствующего атрибута снижает

уровень неопределенности множественного выбора в г-й ситуации

на величину ДЯ

(

. Если неравенство в противоположную сторону,

то такое же самое изменение атрибута увеличивает уровень неопре-

деленности.

Величину ДЯ, будем называть

предельным информационным

эф-

фектом, имея в виду, с одной стороны, содержательный смысл

этой величины, а с другой — механизм ее определения через

предельный эффект атрибута. Понять, в каких ситуациях следу-

ет ожидать отрицательное значение предельного информационного

эффекта, а в каких — положительное, весьма сложно. Гораздо

проще вычислить ДЯ

(

. как разность между значениями, определя-

емыми в соответствии с (3.108) и (3.107). И все же рассмотрим

механизм формирования величины предельного информационно-

го эффекта

ДЯ, = - Е (Р//+ 8

) log

(P^+ S^+i

Iog

7=0 7=0

= -£(P//+<%)iog

р У*П

7=0

-SPylogjP//- S^lO&V i(

(/)

7=0 7=0 7=0

Py+Sy

P„

+ SP//log

7=0

7=0 7=0

(Py+S^

P„

(3.109)

Полученное значение должно быть отрицательным, чтобы уве-

личение соответствующего атрибута снизило неопределенность

ситуации множественного выбора. Знак выражения (3.109) зави-

сит от 8,у. Причем одновременно для всех j предельный эффект 8..

не может иметь один и тот же знак^ так как в его составе сомно-

житель, равный отклонению b

Для каждой

i-Pt

ситуации множественного выбора можно запи-

сать

ДЯ,=- £ V°S2V 2 (Py+^)log

jer

jeJ

106

- S S

\og

X (P//+5^)log

JEJ

jeJ-

(3.110)

где J~(J

) — множество тех вариантов, для которых by ~ b, име-

ет отрицательный (положительный) знак. Следовательно, знак

Д//, определяется знаком верхних слагаемых, если они по величи-

не превосходят нижние, и наоборот, если не превосходят. Зна-

чения этих сумм различны для разных /, а это значит, что в од-

них ситуациях предельный эффект будет направлен на снижение

неопределенности, а в других — на повышение.

В моделях множественного выбора энтропийный анализ играет

важную роль, так как лицу, принимающему решение на основе

результатов моделирования, необходимы оценка уровня неопреде-

ленности смоделированной ситуации и возможные варианты ее

снижения.

3.5.2. Модели множественного выбора

в задачах оценки инвестиционных проектов

Рассмотрим прикладные возможности модели множе-

ственного выбора на следующем примере.

ОАО "Жемчужина" приняло решение об открытии нескольких

точек общественного питания, предварительно получив разреше-

ние на строительство одной из этих точек в центре г. Воронежа,

второй — в городском районе, удаленном от центра, и третьей —

на Ростовской автотрассе (недалеко от города). В каждом из

указанных мест можно реализовать один из трех вариантов: от-

крыть или ресторан, или кафе, или бистро. В свою очередь, на

эффективность выбранного варианта влияют различные факторы,

среди которых можно выделить наиболее существенные, связан-

ные с выбором типа кухни (национальной, традиционной и сме-

шанной), ориентации на потенциальных посетителей (имеющих

высокие, средние и ниже среднего доходы), а также максималь-

ное количество обслуживаемых одновременно клиентов.

Руководству ОАО "Жемчужина" необходимо для каждого мес-

та, отведенного под строительство, выбрать вариант, который с

наименьшим риском обеспечит прибыльное долговременное фун-

кционирование соответствующей точки общественного питания.

Для объективной оценки риска было решено изучить все аспекты,

связанные с этим бизнесом в г. Воронеже.

107

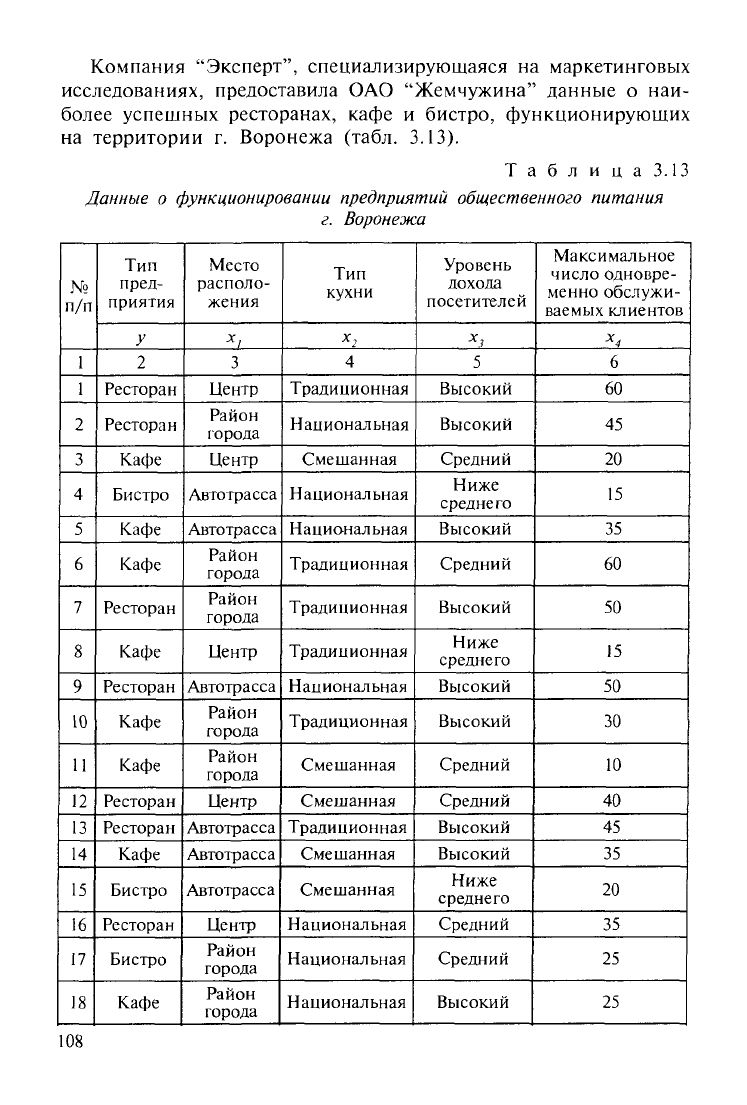
Компания

"Эксперт",

специализирующаяся

на

маркетинговых

исследованиях,

предоставила

ОАО

"Жемчужина"

данные

о наи-

более успешных

ресторанах,

кафе

и бистро,

функционирующих

на

территории

г.

Воронежа

(табл.

3.13).

Таблица

3.13

Данные

функционировании предприятий общественного питания

г.

Воронежа

№

п/п

Тип

пред-

приятия

Ресторан

Кафе

Бистро

Кафе

Ресторан

Кафе

Ресторан

Кафе

Ресторан

Кафе

Бистро

Ресторан

Бистро

Кафе

Место

располо-

жения

х,

Центр

Район

города

Центр

Автотрасса

Район

города

Район

города

Центр

Автотрасса

Район

города

Район

города

Центр

Автотрасса

Центр

Район

города

Район

города

Тип

кухни

Традиционная

Национальная

Смешанная

Национальная

Традиционная

Национальная

Традиционная

Смешанная

Традиционная

Смешанная

Национальная

Уровень

дохода

посетителей

Высокий

Средний

Ниже

среднего

Высокий

Средний

Высокий

Ниже

среднего

Высокий

Средний

Высокий

Ниже

среднего

Средний

Высокий

Максимальное

число

одновре-

менно

обслужи-

ваемых клиентов

108

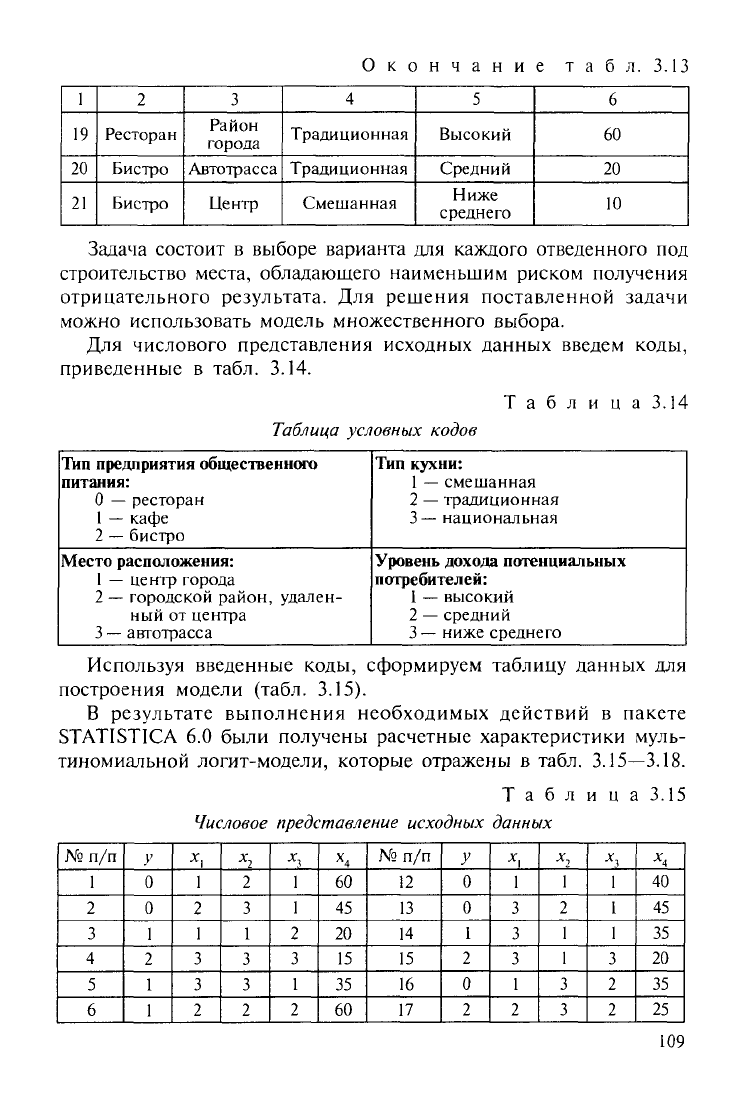
Окончание табл. 3.13

Ресторан

Бистро

Район

города

Автотрасса

Центр

Традиционная

Смешанная

Высокий

Средний

Ниже

среднего

Задача состоит в выборе варианта для каждого отведенного под

строительство места, обладающего наименьшим риском получения

отрицательного результата. Для решения поставленной задачи

можно использовать модель множественного выбора.

Для числового представления исходных данных введем коды,

приведенные в табл. 3.14.

Т а б л и ц а 3.14

Таблица условных кодов

Тип предприятия общественного

питания:

0 — ресторан

1 — кафе

—

бистро

Место расположения:

1 — центр города

—

городской район, удален-

ный от центра

—

автотрасса

Тип кухни:

—

смешанная

—

традиционная

—

национальная

Уровень дохода потенциальных

потребителей:

1 — высокий

—

средний

3—

ниже среднего

Используя введенные коды, сформируем таблицу данных для

построения модели (табл. 3.15).

В результате выполнения необходимых действий в пакете

STATIST1CA 6.0 были получены расчетные характеристики муль-

тиномиальной логит-модели, которые отражены в табл. 3.15—3.18.

Таблица 3.15

Числовое представление исходных данных

№ п/п

109