Davim J.P.Machining of Hard Materials

Подождите немного. Документ загружается.

5 Finite-element Modeling and Simulation 157

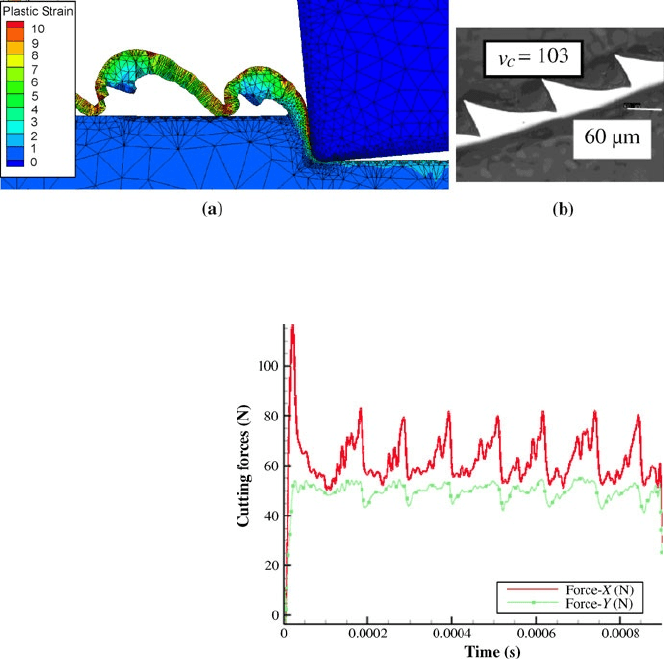
every feed and cutting speed and induces variations in the cutting forces ob-

tained, since the amount of material machined varies continuously. In Fig-

ure 5.13 these variations can be observed: roughly 20

N in the cutting force and

N in the feed force.

The serrated chip is quite common in hard turning and has been observed in

several research works [21].

5.3.3 Three-dimensional Finite-element Analysis

of Hard Turning

In order to show residual stresses in machined surfaces, 3D simulations should be

run. In this case, DEFORM-3D has been employed to provide residual stresses (as

well as results for forces, temperatures, etc.) during hard turning. The experimen-

tal plan can be observed in Table 5.3. Four simulations were carried out with

Figure 5.12 (a) Serrated chip obtained with the round cutting edge (AdvantEdge: cutting speed

of 100 m min

–1

, feed rate of 0.1

mm and cutting radius of 25

μm), and (b) serrated chip obtained

at v

103

m min

–1

and feed rate of f

0.1

Figure 5.13 Cutting (X) and

feed (Y) forces obtained

158 P.J. Arrazola

DEFORM-3D, varying the cutting speed (v) from 120 to 140

m/min, and the feed

rate (f) from 0.1

mm/rev to 0.15

mm. The depth of cut was kept constant at the

value of 0.2

mm.

A comparison with previous research work with Abaqus/Explicit™ will be made:

cutting speed (v) of 120

m/min., a feed rate (f) of 0.1

mm/rev and a depth of cut (p) of

0.2

mm [38]. Data about the Abaqus/Explicit model is shown in Table 5.3.

Table 5.3 Material properties and cutting condition for the process simulations (Abaqus/Expli-

cit and DEFORM-3D)

Abaqus/Explicit,

DEFORM-3D

A (MPa) 2482.4

B (MPa) 1498.5

n 0.19

C 0.027

Plasticity,

Johnson–Cook law

m 0.66

Inelastic heat fraction (β) 0.9

Density (ρ)

(kg m

–3

)

Workpiece

(AISI 52100 62HRC)

Tool (PCBN)

7827

3120

201.33 f

(T)

Elasticity (E)

(GPa)

Workpiece

Tool

680

Conductivity (k)

(W m

–1

)

Workpiece

Tool

100

Specific heat

–1

)

Workpiece

Tool

458

960

Material

properties

Expansion (K

–1

)

Workpiece

Tool

11.5

–6

f(T)

4.9

–6

Thermal conductance (K

) (W m

–2

–1

) 1

Heat partition coefficient (Г) 0.5

Friction coefficient (µ) 0.35 (Guo)

Contact

Friction energy transformed into heat (η) 1

Cutting speed (v) (m/min) 120/140

Feed rate (f) (mm/rev) 0.1/0.15

Depth of cut (p) (mm) 0.2

Cutting-edge microgeometry Chamfer 20°

0.1

Nose radius (r

) (mm) 0.8

Rake angle (γ) (°) –5

Clearance angle (α) (°) 5

Cutting-edge inclination angle (λ

) (°) –5

Process

Cutting-edge angle (К

) (°) 0

5 Finite-element Modeling and Simulation 159

Table 5.4 Experimental plan and results obtained for Abaqus/Explicit and DEFORM-3D

Cutting forces Tool Workpiece Chip Test

(N)

Temp

(K)

Temp

(K)

ε σ

(GPa)

Temp

(K)

ε σ

(GPa)

Vc_120_F_010

(Abaqus/Explicit)

154 58 138 1558 – – – 1483 – –

Vc_120_F_010

(DEFORM-3D)

138 47 108 1065 963 4.8 1.39 1128 6.8 2.31

Vc_120_F_015

(DEFORM-3D)

192 59 147 1060 971 5.24 1.48 1139 6.3 2.19

Vc_140_F_010

(DEFORM-3D)

134 46 102 1156 993 5.72 1.63 1190 6.4 2.08

Vc_140_F_015

(DEFORM-3D)

188 56 142 1116 1012 6.3 1.7 1167 6.6 1.92

Table 5.5 shows the Von Mises stress contours obtained with the Abaqus

model. The approach employed is as follows. Firstly, after an Abaqus/Explicit step

is finished, the model is imported into Abaqus/Standard™. Once the import is

completed, a new mesh is designed taking into account the deformed state of the

previous mesh. For this task, a high-performance finite-element pre-processor is

employed, Altair Hypermesh 8.0™, which permits the creation of surfaces from a

previous mesh. After the desired mesh is created, a mapping calculation is made in

Abaqus/Standard, in order to interpolate the solution onto the new mesh from the

output databases generated with the old mesh. Finally, the analysis is imported

into Abaqus/Explicit and a new step is performed. This procedure is repeated until

desired steady-state solution has been reached [38].

The ALE formulation employed for the final step (see Table 5.5) makes the

material enter the workpiece mesh and exit it via different Eulerian boundary

surfaces.

Table 5.5 Initial mesh, remeshing steps, and final steady-state step for the ALE finite-element

model for 3D hard turning

Step Total time

Fully

Eulerian

bounda-

ries

0.165

(0.33

mm)

160 P.J. Arrazola

Thanks to this new hybrid formulation employed, artificial criteria (physical or

geometrical) to generate the chip or an initial chip design are not needed. Only

a short initial remeshing stage is needed to obtain the final chip shape. Such fea-

tures, probably the major advantages of the presented model over the ones re-

ported in the literature [18, 59], avoid the introduction of arbitrary effects on the

obtained results, making the simulation more robust. This point gains special

relevance when trying to forecast the state of the machined surface and residual

stresses.

More detailed information about this work can be found in [38, 58].

Both tool and workpiece are considered as deformable, in order to analyze the

stresses that appear in the tool. Only elastic properties are used for the tool.

Due to the limitations imposed by the importing options in Abaqus/Standard, in

these 3D simulations the Johnson–Cook law has been discretized into tabular data.

The number of points employed to describe the material behavior is 15,525, with

25 levels for the strain, 23 for the strain rate, and 27 for the temperature.

The Coulomb friction law has been employed for the modeling of the tool–chip

interface contact. Heat transfer is allowed on the tool–chip contact area.

The elements employed are C3D8RT, eight-node bricks with tri-linear dis-

placement, temperature calculation, and hourglass control. Their size varies from

µm to 30

µm depending on the zone. Table 5.3 shows the input parameters for

the hard-turning simulation [59].

5.3.4 Three-dimensional Finite-element Analysis

of Hard Turning: Results and Discussion

The simulation was run until the steady state was reached: 0.133

ms in the case of

Abaqus/Explicit, and 0.25

ms in the case of DEFORM-3D. Results for forces and

temperatures in Figures 5.14 and 5.15, respectively, confirm that the steady state

has been reached. As seen in Figure 5.14, for DEFORM-3D the cutting force

seems to stabilize around 140

N with small perturbations of about 2

The cutting force obtained from the hard-turning simulation with Abaqus/Ex-

plicit is 154

N, while the feed force has a value of 58

N. The radial force has

a value of 138

N, which is almost as big as the cutting force. For DEFORM-3D

simulations, values of cutting force vary from 192 to 134

N, while the radial force

varies from 147 to 108

N. The feed force varies between the values of 47

N and

N. It can be observed (Figure 5.16), that as the feed increases, the values of the

forces raise in a similar way. The results for the cutting force match qualitatively

well with results obtained experimentally by Huang and Liang [58]. However,

differences are more significant when comparing feed force and passive (radial)

forces. Lower values are obtained in FEM. It is clear that the use of better friction

models with proper identification friction parameters would have given results

closer [58] to the experimental ones.

5 Finite-element Modeling and Simulation 161

Figure 5.14 Cutting forces for DEFORM-3D

Figure 5.15 Workpiece maximum temperature plot for DEFORM-3D

What is more, looking at Figure 5.17, it can be said that the rise in the cut-

ting speed causes a slight decrease in the values of the cutting forces. This

means that the increase in the forces depends more on the feed, rather than on

the cutting speed.

Figure 5.18 to 5.22 show the temperature fields for the hard-turning simula-

tion in the tool and workpiece for the five cases studied. In the case of the

DEFORM results, tool temperature varies form 1065

K to 1116

K. Differences

with Abaqus/Explicit are again quite relevant (>400

K) and are due again, as in

2D, to differences in input parameters, solver, etc.

162 P.J. Arrazola

100

120

140

160

180

200

51.01.0

Cutting forces (N)

Feed (mm/rev)

Fc 120 m/min

Fp 120 m/min

Ff 120 m/min

Fc 140 m/min

Fp 140 m/min

Ff 140 m/min

Figure 5.16 Influence of feed on cutting forces for DEFORM-3D simulations

100

150

200

250

041021

Cutting speed (m·min

-1

)

Cutting forces (N)

Fc 0.1 feed

Ff 0.1 feed

Fp 0.1 feed

Fc 0.15 feed

Ff 0.15 feed

Fp 0.15 fee

Figure 5.17 Influence of cutting speed on cutting forces for two different feeds for DEFORM-

3D simulations

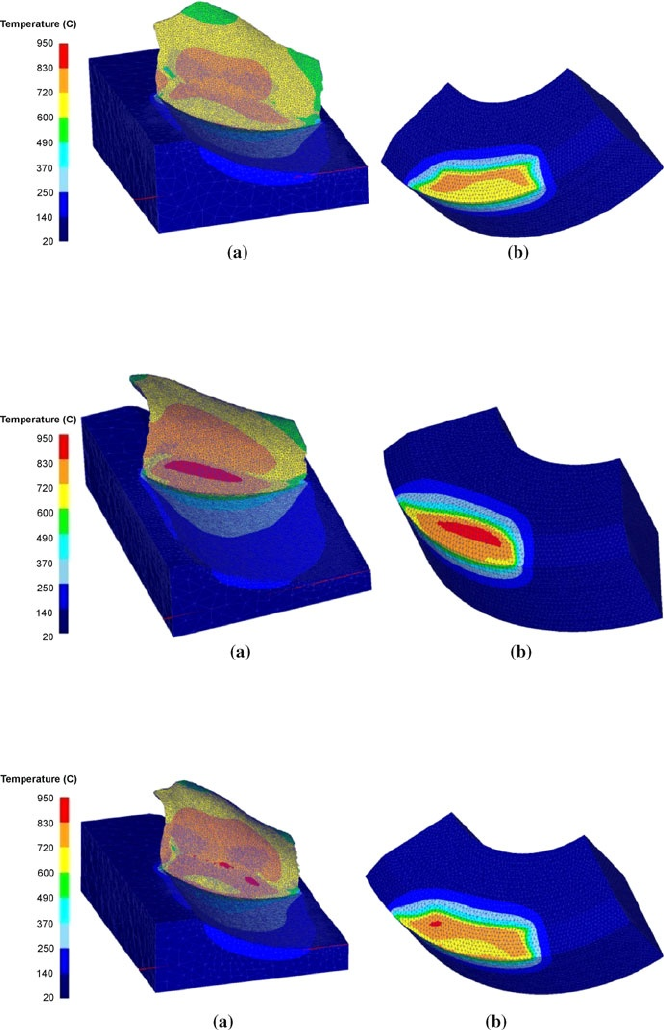
Figure 5.18 Temperature (°C) contour maps in the workpiece (a) and tool (b) for Vc_120_F_010

(DEFORM-3D) simulation

5 Finite-element Modeling and Simulation 163

Figure 5.19 Temperature (°C) contour maps in the workpiece (a) and tool (b) for Vc_120_F_015

(DEFORM-3D) simulation

Figure 5.20 Temperature (°C) contour maps in the workpiece (a) and tool (b) for Vc_140_F_010

(DEFORM-3D) simulation

Figure 5.21 Temperature (°C) contour maps in the workpiece (a) and tool (b) for Vc_140_F_015

(DEFORM-3D) simulation

164 P.J. Arrazola

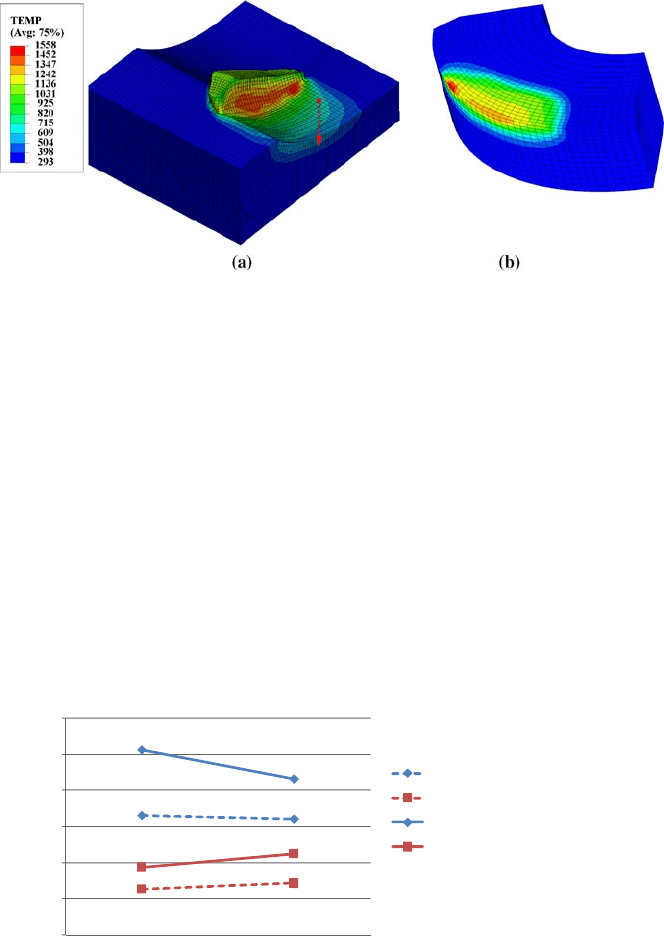
Figure 5.22 Temperature (K) contour maps in the workpiece (a) and tool (b) for Vc_120_F_010

(Abaqus/Explicit) simulation; arrow indicates the path used for the residual-stress extraction

Figure 5.23 shows the temperature results obtained depending on the feed rate.

It is observed that when feed rate rises, the values of temperature in the tool seem

to decrease slightly, while workpiece temperatures appear to increase.

On the other hand, when the cutting speed is increased, there is a significant in-

crease in temperature results, as can be observed in Figure 5.24.

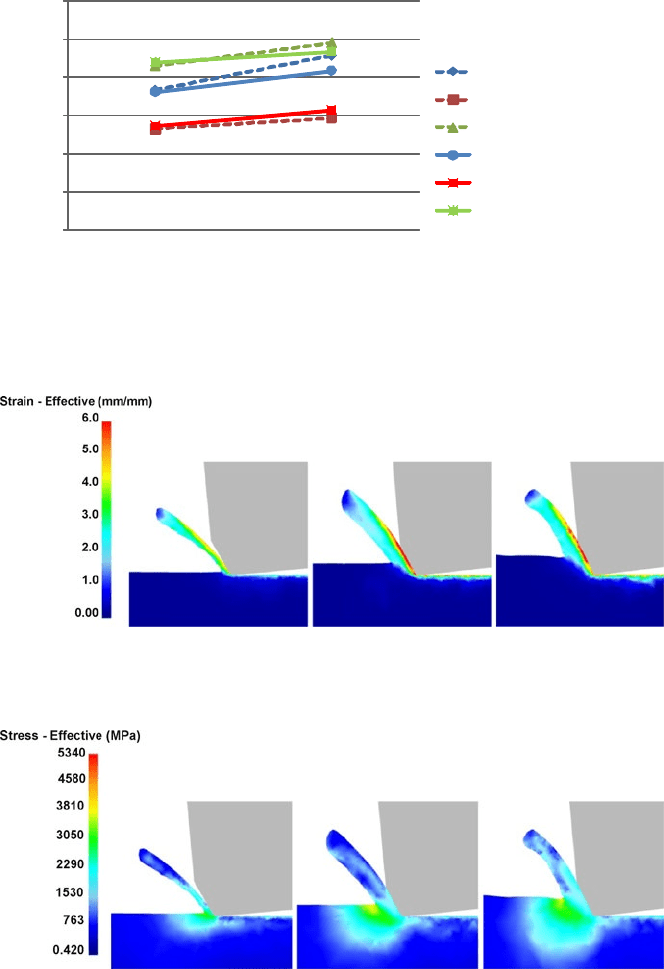
One of the main advantages of 3D simulations is that it is possible to analyze

the variable state of the chip formation process along the cutting edge. Fig-

ures 5.25 and 5.26 show the plastic strain and Von Mises equivalent stress contour

maps for different cutting planes (perpendicular to the cutting edge) for the test

with a cutting speed of v

120

m min

–1

. The maximum plastic strain reaches the

value of 6, and is generated where the undeformed chip thickness is a maximum.

On the other hand, the maximum stress appears in the tool, in the central zone

of the chip width.

900

950

1000

1050

1100

1150

1200

51,01,0

Tempera tures (K)

Feed (mm/rev)

Tool 120 m/min

Workpiece 120 m/min

Tool 140 m/min

Workpiece 140 m/min

Figure 5.23 Influence of feed on temperatures for DEFORM-3D simulations

5 Finite-element Modeling and Simulation 165

Temp era tu res (K)

700

800

900

1000

1100

1200

1300

041021

Cutting speed (m·min

-1

)

Tool 0.1 f ee d

Part 0.1 feed

Chip 0.1 feed

Tool 0.15 feed

Part 0.15 feed

Chip 0.15 feed

Figure 5.24 Influence of cutting speed on temperatures for two different feeds for DEFORM-

3D simulations

Figure 5.25 Plastic-strain equivalent stress for three different cross-sections along the cutting

edge for Vc_120_F_010 (DEFORM-3D)

Figure 5.26 Von Mises equivalent stress for three different cross-sections along the cutting edge

for Vc_120_F_010 (DEFORM-3D)

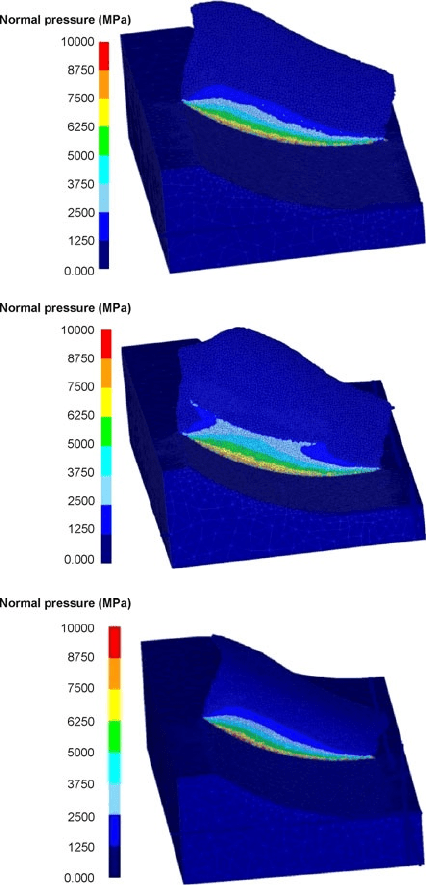
166 P.J. Arrazola

In DEFORM-3D simulations, the tool is rigid so it is impossible to analyze the

contact pressure in the tool. However, Figures 5.27–5.31 show the contact pressure

fields that appear in the workpiece. Comparison of Figure 5.27 and 5.29 (feed of

0.10

mm/rev) and Figure 5.28 and 5.30 (feed of 0.15

mm/rev) reveals that feed rate

does not have a significant influence on contact pressure; similar values are obtained

in all the cases (close to 8–9

GPa). In Figure 5.31 contact pressure obtained with the

Abaqus model is shown. Values close to 8–9

GPa are obtained here as well.

Figure 5.27 Contact

pressure on the workpiece

for Vc_120_F_010

(DEFORM-3D)

Figure 5.28 Contact

pressure on the workpiece

for Vc_120_F_015

(DEFORM-3D)

Figure 5.29 Contact

pressure on the workpiece

for Vc_140_F_010

(DEFORM-3D)