Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


12.4 Solutions of Differential Equations 403
We may multiply both sides by y
0
, known as an integrating factor, which makes
both sides easily integrable in closed form:
2yy
0
+ 2y
0
y
00
2
p
y
2
+ (y
0
)
2
= −y
0
.
The left-hand side is the derivative of
p
y
2
+ (y
0
)
2
. As y is a function of x and we
are about to introduce constants independent of x, it is helpful to switch notation
and use y(x) and y
0
(x) in place of y and y
0
.
Integrate both sides with respect to x from 0 to x to obtain
q
y(x)
2
+ y
0
(x)
2
− kΓk = γ
0
− y(x).
Take kΓk to the other side, square, and simplify to obtain
y
0
(x)
2
= c
2
− 2cy(x) where c = kΓk + γ
0
.
Hence
y
0
(x)
p
c
2
− 2cy(x)
= ±1.
Integrating again from 0 to x yields
−1
c
q
c
2
− 2cy(x) +
1
c
p
c
2
− 2cγ
0
= ±x.
It looks like we may get multiple solutions (which we know isn’t the case), but let
us persevere. Notice that
p
c
2
− 2cγ
0
=
q
kΓk
2
− γ
2
0
= ±γ
1
.
Use this identity and simplify to obtain
c
2
− 2cy(x) = (±cx + γ
1
)
2
= c
2
x
2
± 2cγ
1
x + c
2
− 2cγ
0
.
Solving for y produces
y(x) =
−c
2
x
2
± γ
1
x + γ
0
.
The condition that y
0
(0) = γ
1
shows that the sign is + and the unique solution is
the quadratic
y(x) =
−
q
γ
2
0
+ γ
2
1
− γ
0
2
x
2
+ γ
1
x + γ
0
.
Notice that this solution depends continuously on the initial data (γ
0
, γ
1
). This is a
general phenomenon that we explore in Section 12.7.

404 Differential Equations
Exercises for Section 12.4
A. Consider the DE y
0
= 1 + xy and y(0) = 0 on [−1, 1].
(a) Show that the associated integral operator is a contraction mapping.
(b) Find a convergent power series expansion for the unique solution.
(c) Use the Global Picard Theorem to show that there is a unique solution on [−b, b]
for any b < ∞. Hence deduce that there is a unique solution on R.
B. Consider the DE y
00
= y
0
+ xy + 3x
2
, y(0) = 2 and y
0
(0) = 1 for x ∈ [0, 2].
(a) Find the function Φ and vector Γ to put this DE in standard form.
(b) Calculate the constants involved in the proof of the Global Picard Theorem, and
hence find an integer N such that kF
∗
− F
N
k
∞
< 10
−3
.
C. Consider the DE: xyy
0
= (2 − x)(y + 2) and y(1) = −1.
(a) Separate variables and deduce that the solution y satisfies
e
y/2
y + 2
= xe
x/2
.
(b) Prove that both x and y are bounded.
HINT: In part (a), minimize the left-hand side and maximize the right-hand side.
D. Consider the DE f
0
(x) = xf(x) + 1 and f(0) = 0.
(a) Use the Global Picard Theorem to show that there is a unique solution on [−b, b]
for any b < ∞. Hence deduce that there is a unique solution on R.
(b) Find an explicit power series that solves the DE.
HINT: Look for a solution of the form f(x) =
∞
P
n=0
a
n
x
n
. Plug this into the DE and
find a recurrence relation for the a
n
. Hence obtain a formula for each a
n
.
(c) Show that this series converges uniformly on the whole real line. Hence validatethe
term-by-term differentiation to verify that this power series is the unique solution.
E. (a) Suppose ϕ is C
∞
function on [a, b] ×R, and T f(x) = c +
Z
x
a
ϕ(t, f(t)) dt. Show
by induction that if f
0
∈ C[a, b], then T
n
f
0
has n continuous derivatives.
(b) Hence conclude that a fixed point f = T f must be C
∞
.
F. (a) In the previous question, suppose that ϕ is C
n
. Prove that a solution to f = T f
has n + 1 continuous derivatives.
(b) Let ϕ(t) = t for t ≤ 1 and ϕ(t) = 2 − t for t ≥ 1. Solve the DE y
0
= ϕ(y) and
y(0) = 1.5 on R. Verify that the solution is C
1
but is not twice differentiable.
G. Let p be a positive real number. Suppose that u(x) is a solution of the integral equation
u(x) =
Z
x
0
sin(u(t))u(t)
p
dt.
(a) Fix a > 0 and set M = sup{|u(x)| : |x| ≤ a}. Prove that |u(x)| ≤
M
pn
|x|
n
n!
on
[−a, a] for each n ≥ 0. HINT: |sin y| ≤ |y|
(b) Hence prove that u = 0.
H. Suppose that Φ and Ψ are Lipschitz functions defined on [a, b] × R. Let f and g
be solutions of f
0
= Φ(x, f(x)) and g
0
= Ψ(x, g(x)), respectively. Suppose that
f(a) ≤ g(a) and Φ(x, y) ≤ Ψ(x, y) for all (x, y) ∈ [a, b]×R. Show that f(x) ≤ g(x)
for all x ∈ [a, b].
HINT: If f (x) = g(x), what about f
0
(x) and g
0
(x)?
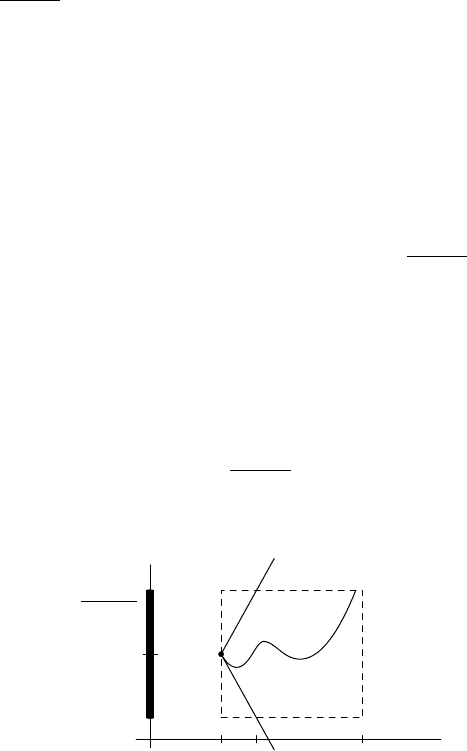
12.5 Local Solutions 405
12.5. Local Solutions
The stipulation that Φ has to be Lipschitz over all of R
n
is quite restrictive.
However, many functions satisfy a Lipschitz condition in y on a set of the form
[a, b] × B
R
(Γ) for R < ∞. For example, if Φ has continuous partial derivatives
of first order, this follows from the Mean Value Theorem and the Extreme Value
Theorem (see the Exercises). In this case, the proof would go through as long as
F
n
(x) always stays in this ball. While this isn’t usually possible for all x, it is
possible to verify this condition on a small interval [a, a + h]. In this way, we get
a local solution. It is then often possible to piece these local solutions together
to extend the solution to all of [a, b]. We shall see in a few examples that such an
extension is not always valid.
12.5.1. LOCAL PICARD THEOREM.
Suppose that Φ is a continuous function from [a, b] ×
B
R
(Γ) into R
n
satisfying a
Lipschitz condition in y. Then the differential equation
F
0
(x) = Φ(x, F (x)), F (a) = Γ
has a unique solution on the interval [a, a + h], where
h = min{b − a, R/kΦk
∞
}.
PROOF. The proof is the same as for the Global Picard Theorem except that we
must ensure that F
n
(x) remains in B
R
(Γ) so that the iterations remain defined. See
Figure 12.2.
xa
h b
y
Γ
B
R
(Γ)
ky − Γk = kΦk
∞
· |x − a|
F
∗
FIGURE 12.2. Schematic setup for Local Picard Theorem.
This follows by induction from the easy estimate for x ∈ [a, a + h]:
kF
n+1
(x) − Γk ≤
Z
x
a
kΦ(t, F
n
(t))kdt
≤ kΦk
∞
|x − a|
≤ kΦk
∞
h ≤ R.
Thus F
n
converges uniformly on [a, a + h] to a solution F
∗
of the differential
equation. The uniqueness argument remains the same. ¥
406 Differential Equations
12.5.2. EXAMPLE. Consider the differential equation
y
0
= y
2
, y(0) = 1, 0 ≤ x ≤ 2.
In this case, the function is Φ(x, y) = y
2
. This is not Lipschitz globally because
Φ(a, n +
1
n
) − Φ(a, n)
(n +
1
n
) − n
> 2n for all n ≥ 1.
However, Φ is continuously differentiable and therefore Lipschitz on any compact
set (Exercise 12.5.A); for example, on [0, 2] ×
B
100
(1). By the Local Picard Theo-
rem, this has a unique solution beginning at the origin. The maximum of |Φ| over
[0, 2] × B
R
(1) is (R + 1)
2
, which leads to h = R/(R + 1)
2
. Our best choice is
R = 1 and h =
1
4
.
This DE may be solved by separation of variables.
y
0
y
2
= 1
Integrating from t = 0 to t = x, we obtain
x =
Z
x
0
1dt =
Z
x
0
y
0
(t) dt
y(t)
2
= −
1
y(t)
¯
¯
¯
¯
x
0
= 1 −
1
y(x)
.
Therefore,
y(x) =
1
1 − x
.
Evidently, this is a solution on the interval [0, 1), which has a singularity at x = 1.
So the solution does not extend in any meaningful way to the rest of the interval.
The range [0, 1) is better than our estimate of [0,
1
4
] but is definitely not a solution
on all of [0, 2].
Now let us consider how to improve on this situation. Start over at the point
1
4
and try to extend the solution some more. More generally, suppose that we have
used our technique to establish a unique solution on [0, a], where a < 1. Consider
the DE
y
0
= y
2
, y(a) =
1
1 − a
, 0 ≤ x ≤ 2.
Again we take a ball B
R
(
1
1−a
) and maximize Φ(y) = y
2
over this ball:
kΦk
B
R
(1/1−a)
=
¡
R +
1
1 − a
¢
2
.
Thus Theorem 12.5.1 applies and extends the solution to the interval [a, a + h],
where h = R/kΦk. A simple calculus argument maximizes h by taking R =
1
1−a
,
which yields h =
1−a
4
.
The thrust of this argument is that repeated use of the Local Picard Theorem ex-
tends the solution to increasingly larger intervals. Our first step produced a solution
on [0, a
1
] with a
1
=
1
4
. A second application extends this to [0, a
2
], where
a
2
= a
1
+
1 − a
1
4
=
3a
1
+ 1
4
=
7
16
.
12.5 Local Solutions 407
Generally, the solution on [0, a
n
] is extended to [0, a
n+1
], where
a
n+1
= a
n
+
1 − a
n
4
=
3a
n
+ 1
4
.
This is a monotone increasing sequence of real numbers that are readily seen to
all be less than 1. Applying the Monotone Convergence Theorem (Theorem 2.5.4)
to the sequence of real numbers (a
n
), there is a limit L = lim
n→∞
a
n
. Therefore,
L = lim
n→∞
a
n+1
= lim
n→∞
3a
n
+ 1
4
=
3L + 1
4
.
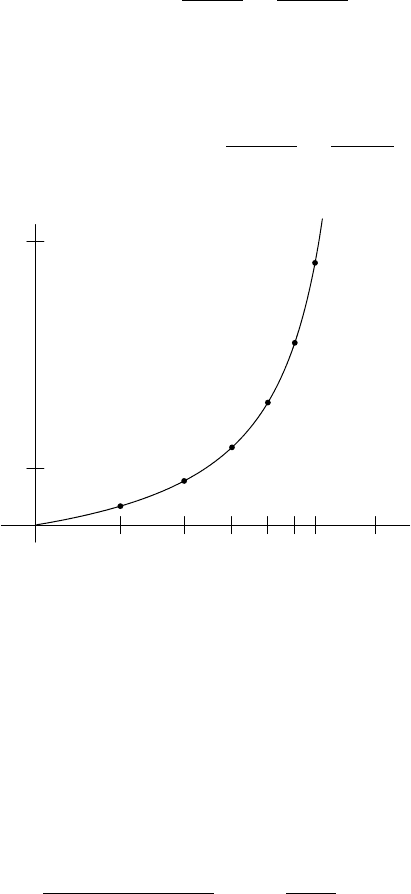
Solving yields L = 1.
x
1
y
1
5
a
1
a
2
a
3
a
4
a
5
a
6
FIGURE 12.3. The solution to y
0
= y
2
, y(0) = 1 with a
n
marked.
The upshot is that repeated use of the Local Picard Theorem did extend the
solution until it blew up by going off to infinity at x = 1. See Figure 12.3. It is
not possible to use our method further since we are essentially following along the
solution curve, which just carried us off the map.
12.5.3. EXAMPLE. Consider the differential equation
y
0
= y
2/3
, y(0) = 0, 0 ≤ x ≤ 2.
The function Φ(x, y) = y
2/3
is not Lipschitz. Indeed,
lim
h→0
|Φ(0, h) − Φ(0, 0)|
|h|
= lim
h→0
1
|h|
1/3
= +∞.
So the Picard Theorems do not apply.
Nevertheless, we may attempt to solve this equation as before. Separating vari-
ables and integrating the equation y
−2/3
y
0
= 1 from 0 to x yields
3y
1/3
= x + c.
The initial data imply that c = 0, and thus y = x
3
/27. This solution is valid on the
whole real line.

408 Differential Equations
However, there is another nice solution that stands out, namely y = 0. So the
solution is not unique. In fact, there are many more solutions as well. For any
a > 0, let
f
a
(x) =
(
0 if x ≤ a
(x − a)
3
/27 if x ≥ a.
Then y = f
a
(x) is a C
2
solution for every positive a.
We see that there can be existence of solutions without uniqueness. A result
known as Peano’s Theorem (see Section 12.8) establishes that the differential equa-
tion F
0
(x) = Φ(x, F (x)) has a solution locally whenever Φ is continuous.
Now we will try to systematize what occurred in Example 12.5.2. The idea
is to make repeated use of the Local Picard Theorem to extend the solution until
either we reach the whole interval or the solution blows up.
12.5.4. DEFINITION. A function Φ(x, y) on [a, b] × R
n
is locally Lipschitz
in the y variable if it is Lipschitz in y on each compact subset [a, b] ×
B
R
for all
positive real numbers R.
Actually a truly local definition of locally Lipschitz in y would say that for each
(x, y) ∈ [a, b] × R
n
, there is a positive number ε > 0 such that Φ is Lipschitz in
y on [x − ε, x + ε] × B
ε
(y). However, a compactness argument shows that this is
equivalent to the definition just given. See Exercise 12.5.J.
12.5.5. CONTINUATION THEOREM.
Suppose that Φ : [a, b] × R
n
→ R
n
is a locally Lipschitz function. Consider the
differential equation
F
0
(x) = Φ(x, F (x)), F (a) = Γ.
Then either
(1) the DE has a unique solution F (x) on [a, b]; or
(2) there is a c ∈ (a, b) so that the DE has a unique solution F (x) on [a, c)
and lim
x→c
−
kF (x)k = +∞.
PROOF. The Local Picard Theorem (Theorem 12.5.1) establishes the fact that there
is a unique solution on a nontrivial interval [a, a + h]. Define c to be the supremum
of all values d for which the DE has a unique solution on [a, d]. A priori, these
might be different solutions for different values of d. However, if F
1
and F
2
are
the unique solutions on [a, d
1
] and [a, d
2
], respectively, for a < d
1
< d
2
, then
the restriction of F
2
to [a, d
1
] will also be a solution. Hence by the uniqueness,
F
2
(x) = F
1
(x) when both are defined. Therefore, we may conclude that there
is a unique solution F
∗
(x) of the DE defined on [a, c) by taking the union of the
solutions for d < c.

12.5 Local Solutions 409
If F
∗
blows up at c, then we satisfy part (2) of the theorem; and if the solution
extends to include b, we have part (1). However, it could be the case that the solu-
tion F
∗
remains bounded on some sequence approaching the point c, contradicting
(2), yet the solution does not actually extend to or beyond the point c. The proof is
complete if we can show that this is not possible. We suppose first that c < b.
Let x
n
be a sequence increasing to c such that kF (x
n
)k ≤ K for n ≥ 1.
Consider the compact region D = [a, b] ×
B
K+1
(0). Since Φ is locally Lipschitz
in y, it is Lipschitz on the region D. Set
M = sup
(x,y)∈D
kΦ(x, y)k and δ = min
n
b − c
2
,
1
2M
o
.
Choose N large enough that c − x
N
< δ. We may apply the Local Picard Theo-
rem 12.5.1 to the DE
F
0
(x) = Φ(x, F (x)) F (x
N
) = F
∗
(x
N
) for x ∈ [x
N
, b].
The result is a unique solution F (x) on the interval [x
N
, x
N
+ h], where
h = min{b − x
N
, 1/M} ≥ δ.
In particular, d := x
N
+ h > c. The uniqueness guarantees that F (x) agrees
with F
∗
(x) on the interval [x
N
, c). Hence extending the definition of F
∗
by setting
F
∗
(x) = F (x) on [x
N
, x
N
+ h] produces a solution on [a, d]. This contradicts the
definition of c.
An easy modification of this argument is possible when c = b showing that the
solution always extends to the closed interval [a, b] if the solution does not blow
up. Take δ = 1/2M . We leave the details to the reader. ¥
The solution obtained in the Continuation Theorem is called the maximal con-
tinuation of the solution to the DE.
12.5.6. EXAMPLE. Not all solutions of differential equations blow up in the
manner of the previous theorem. Consider the DE
x
4
y
00
+ 2x
3
y
0
+ y = 0 and y(
2
π
) = 1 y
0
(
2
π
) = 0 for x ∈ R.
This looks like a reasonably nice linear homogeneous equation (see the next sec-
tion). However, the coefficient of y
00
is not 1, but rather a function of x that vanishes
at 0. To put this in our standard form, we divide by x
4
to obtain
y
00
+
2
x
y
0
+
1
x
4
y = 0.
The function Φ is just
Φ(x, y
0
, y
1
) =
¡
y
1
, −
2
x
y
1
−
1
x
4
y
0
¢
.
410 Differential Equations
This function satisfies
kΦ(x, y
0
, y
1
) − Φ(x, z
0
, z
1
)k =
°
°
¡
y
1
− z
1
,
2
x
(z
1
− y
1
) +
1
x
4
(z
0
− y
0
)
¢
°
°
≤ |y
1
− z
1
|
¡
1 +
2
|x|
¢
+
1
x
4
|z
0
− y
0
|
≤
¡
1 +
2
|x|
+
1
x
4
¢
ky − zk.
So Φ satisfies a global Lipschitz condition in y provided that x remains bounded
away from 0. Thus the Global Picard Theorem (Theorem 12.4.3) applies on the
interval [ε, R] for any 0 < ε <
1
π
< R < ∞. It follows that there is a unique
solution on (0, ∞).
We will not demonstrate how to solve this equation. However, it is easy to
check (do it!) that the solution is f(x) = sin(1/x). This solution has a very nasty
discontinuity at x = 0, but it does not blow up—it remains bounded by 1. This does
not contradict the Continuation Theorem (Theorem 12.5.5). The reason is that the
function Φ is not locally Lipschitz on R × R
2
. It is not even defined for x = 0 and
has a bad discontinuity there. This shows why we cannot expect to have a global
solution to a DE where the coefficient of the highest-order term y
(n)
vanishes.
Exercises for Section 12.5
A. Suppose that Φ(x, y) and
∂
∂y
Φ(x, y) are both continuous functions on the region
[a, b] × [c, d]. Use the Mean Value Theorem to show that Φ is Lipschitz in y.
HINT: Let L =
°
°
∂
∂y
Φ(x, y)
°
°
∞
.
B. Suppose that Φ(x, y
0
, y
1
) is C
1
on [a, b] ×
B
R
(0). Show that Φ is Lipschitz in y.
HINT: Let L =
°
°
∂
∂y
0
Φ(x, y)
°
°
∞
+
°
°
∂
∂y
1
Φ(x, y)
°
°
∞
. Estimate Φ(x, y
0
, y
1
)−Φ(x, z
0
, z
1
)
by subtracting and adding Φ(x, z
0
, y
1
).
C. For each of the following DEs, write down the function Φ and decide if it satisfies (a)
a global Lipschitz condition in y, (b) a local Lipschitz condition in y, or (c) a Lipschitz
condition on a smaller region that allows a local solution.
(a) y
00
= yy
0
and y(0) = y
0
(0) = 1 for 0 ≤ x ≤ 10
(b) y
0
=
p
1 + y
2
and y(0) = 0 for 0 ≤ x ≤ 1
(c) f
0
(x) + f(x)
2
= 4xf(x) − 4x
2
+ 2 and f(0) = 2
(d) (x
2
− x − 2)f
0
(x) + 3xf(x) − 3x = 0 and f(0) = 2 for −10 ≤ x ≤ 10
D. Solve Exercise C(c) explicitly. Find the maximal continuation of the solution.
HINT: Find the DE satisfied by g(x) = f(x) − 2x and solve it.
E. Solve Exercise C(d) explicitly. Find the maximal continuation of the solution.
HINT: Find the DE satisfied by g(x) = f(x) − 1 and solve it.
F. Reformulate Theorem 12.5.1 so that it is valid when the initial conditions apply to a
point c in the interior of [a, b].
12.6 Linear Differential Equations 411
G. Consider y
0
= sin
µ
x
3
+ x
2
− 1
p
101 − y
2
¶
and y(2) = 3. Prove that there is a solution on
[−5, 9]. HINT: Show that |y| ≤ 10 first. Then obtain a Lipschitz condition.
H. Provide the details for the proof of Theorem 12.5.5 for the case c = b.
HINT: Let δ = 1/(2M ).
I. Consider the DE y
0
= 3xy
1/3
for x ∈ R and y(0) = c ≥ 0. Let A
ε
= {y : |y| ≥ ε}.
(a) Show that 3xy
1/3
is Lipschitz in y on [a, b] × A
ε
but not on [a, b] × [−1, 1].
(b) Solve the DE when c > 0.
(c) Find at least two solutions when c = 0.
J. Show that the two definitions of locally Lipschitz given in Definition 12.5.4 and the
subsequent paragraph are equivalent. HINT: Cover [a, b] ×
B
R
(0) by open sets on
which Φ is Lipschitz in y. Use the Borel–Lebesgue Theorem (Theorem 9.2.3).
K. Consider the DE f(x)f
0
(x) = 1 and f(0) = a for x ∈ R.
(a) Solve this equation explicitly.
(b) Show that there is a unique solution on an interval about 0 if a 6= 0 but that it only
extends to a proper subset of R, even though the solution does not blow up. Why
does this not contradict the Continuation Theorem?
(c) Show that there are two solutions for a = 0 valid on [0, ∞).
Why does this not contradict the Local Picard Theorem?
L. Show that f(x) = 1 −
√
1 − x
2
for −1 ≤ x ≤ 1 is the unique solution of the DE
y
00
=
¡
1 + (y
0
)
2
¢
3/2
and y(0) = y
0
(0) = 1. This solution cannot be continued beyond
x = 1, yet |f(x)| ≤ 1. Why does this not contradict the Continuation Theorem?
HINT: How does F (x) =
¡
f(x), f
0
(x)
¢
behave at x = 1?
M. Consider the DE: y
0
= x
2
+ y
2
and y(0) = 0.
(a) Show that this DE satisfies a local Lipschitz condition but not a global one.
(b) Integrate the inequality y
0
≥ 1 + y
2
for x ≥ 1 to prove that the solution must go
off to infinity in a finite time. (See Exercise 12.4.H.)
12.6. Linear Differential Equations
In this section, we explore a very important class of differential equations in
greater depth. This class occurs frequently in applications and is also especially
amenable to analysis.
Consider the differential equation
f
(n)
(x) = p(x)+q
0
(x)f(x)+q
1
(x)f
0
(x)+···+q
n−1
(x)f
(n−1)
(x)(12.6.1)
f(c) = γ
0
, f
0
(c) = γ
1
, ···f
(n−1)
(c) = γ
n−1
,
where p(x) and q
k
(x) are continuous functions on [a, b] and c is a point in [a, b].
This is called a linear differential equation because the function
ϕ(x, y) = p(x) + q
0
(x)y
0
+ q
1
(x)y
1
+ ··· + q
n−1
(x)y
n−1
defined on [a, b] × R
n
is linear in the second variable y = (y
0
, y
1
, . . . , y
n−1
).
412 Differential Equations
Using the reduction in Section 12.3, we obtain the reformulated first-order dif-
ferential equation
F
0
(x) = Φ(x, F (x)) and F (c) = Γ = (γ
0
, γ
1
, . . . , γ
n−1
),
where
Φ(x, y
0
, . . . , y
n−1
) =
¡
y
1
, . . . , y
n−1
, ϕ(x, y)
¢
.
We will verify that Φ is Lipschitz in y. Set M = max
0≤k≤n−1
kq
k
k
∞
. Then for
any x ∈ [a, b] and y = (y
0
, . . . , y
n−1
) and z = (z
0
, . . . , z
n−1
) in R
n
,
kΦ(x, y) − Φ(x, z)k =
°
°
°
¡
y
1
− z
1
, . . . , y
n−1
− z
n−1
,
n−1
X
k=0
q
k
(x)(y
k
− z
k
)
¢
°
°
°
=
³
n−1
X
i=1
|y
i
− z
i
|
2
+
¯
¯
¯
n−1
X
k=0
q
k
(x)(y
k
− z
k
)
¯
¯
¯
2
´
1/2
≤
¡
ky − zk
2
+ (nM ky − zk)
2
¢
1/2
≤ (1 + nM)ky − zk.
So Φ satisfies the Lipschitz condition with L = 1 + nM.
Therefore, by the Global Picard Theorem (Theorem 12.4.3), this equation has
a unique solution for each choice of initial values Γ.
The most important consequence of linearity is the relationship between so-
lutions of the same DE with different initial values. Suppose that f and g are
solutions of (12.6.1) with initial data Γ and ∆ = (δ
0
, . . . , δ
n−1
), respectively. Then
the function h(x) = g(x) − f(x) satisfies
h
(n)
(x) = p(x) +
n−1
X
k=0
q
k
(x)g
(k)
(x) − p(x) +
n−1
X
k=0
q
k
(x)f
(k)
(x)(12.6.2)
= q
0
(x)h(x) + q
1
(x)h
0
(x) + ··· + q
n−1
(x)h
(n−1)
(x)
and satisfies the initial conditions
h
(k)
(c) = γ
k
− δ
k
for 0 ≤ k ≤ n − 1.
This is a linear equation with the term p(x) missing. This DE satisfied by h is
called a homogeneous linear DE, while the equation (12.6.1) with the forcing
term p(x) 6= 0 is called a nonhomogeneous linear DE.
Generally the homogeneous DE is much easier to solve. Once the set of solu-
tions for the homogeneous problem is described as an n-dimensional linear space,
one searches for a single solution f
p
of the nonhomogeneous DE (12.6.1) without
regard to the initial conditions. This solution is called a particular solution, to dis-
tinguish it from the general solution. Then the argument of the previous paragraph
shows that the general solution of this DE has the form f
p
+ h for some solution h
of the homogeneous DE (12.6.2).
Let Γ
i
denote the initial conditions γ
i
= 1, γ
j
= 0 for j 6= i, 0 ≤ j ≤ n − 1.
In other words, the vectors Γ
i
correspond to the standard basis vectors of R
n
. For
