Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

11.7 Iterated Function Systems 383

Fix ε > 0 and choose N so large that s

diam(A) < ε. By Exercise 11.1.E,

each T

is a contraction with Lipschitz constant no greater than s

. Consequently,

diam(T

A) ≤ s

diam(A) < ε. If a ∈ A, choose a word w of length N so

that a ∈ T

A. Since a

= T

, it is clear that a

∈ T

A as well. Therefore,

ka − a

k < ε. Thus the set of these ﬁxed points is dense in A.

Now if a is an arbitrary point in A, it follows that T

a belongs to A for every

ﬁnite word w. Hence O(a) ⊂ A. Observe that T

a = T

a is another point in

O(a). Therefore, T O(a) ⊂ O(a). Let B =

O(a). The continuity of T implies that

T B ⊂ B. By Corollary 11.7.5, A =

k≥1

B ⊂ B. In particular A ⊂ B ⊂ A,

and so

O(a) = A. ¥

This result allows us graph the fractal approximately as follows. Pick any point

a. This may not lie in A. However, b = T

100

a will be very close to the ﬁxed

point of T

assuming reasonable constants. Use a computer to calculate b and then

recursively plot the sets T

{b} for sufﬁciently many k. This will frequently give

an excellent picture of the fractal. You can make explicit estimates to ensure good

convergence.

11.7.7. EXAMPLE. Consider the maps

.5 −.5

.5 .5

¸·

.5 −.5

.5 .5

¸·

−1

A simple matrix calculation shows that (−4, 6) is the ﬁxed point of T

and (−4, 2)

is the ﬁxed point of T

. We use a computer to plot the sets A

= {(−4, 6), (−4, 2)}

and A

k+1

= T

∪ T

for 1 ≤ k ≤ 11. Since A equals the closed union of

all the A

’s, this yields a reasonable approximation. Look for the self-symmetry in

Figure 11.12.

We ﬁnish with a simple result that shows that the sets that are ﬁxed for iterated

function schemes are extremely plentiful.

11.7.8. PROPOSITION. Let C be a compact subset of R

, and let ε > 0. Then

there is an IFS T = {T

, . . . , T

} with ﬁxed set A such that d

(A, C) < ε.

PROOF. Since C is compact, we can ﬁnd a ﬁnite set of points, C

= {c

, . . . , c

so that the union of the balls B

), call it B, contains C. Observe that B equals

)

. Let R be large enough so that B

(0) contains B. Deﬁne

x =

(x − c

) + c

for 1 ≤ i ≤ r.

Since T

= c

are ﬁxed points, C

is contained in the ﬁxed set A of T .

Also, T

B ⊂ T

(0) ⊂ B

) ⊂ B for each i. Therefore by Corollary 11.7.5,

A ⊂ B = (C

)

⊂ C

. Plus, C ⊂ (C

)

⊂ A

. So, d

(A, C) < ε as required. ¥

384 Discrete Dynamical Systems

−5

FIGURE 11.12. Pointillist picture of “the twin dragon” set.

Exercises for Section 11.7

A. (a) Let A

, A

, B

and B

be compact subsets of R

. Show that

∪ A

, B

∪ B

) ≤ max

, B

), d

, B

)

(b) Use induction to prove Lemma 11.7.3.

B. (a) Let T = {T

, . . . , T

} be an IFS on R

. Suppose that B is a compact set. Prove

that there is a unique compact set C such that C = B ∪ T C.

HINT: Add a constant map T

(X) = B for X ∈ K(R

(b) Hence prove that there is always a compact set C containing B so that T C ⊂ C.

C. Consider the four maps on R

given by T

x = Ax + b

for i = 1, 2, 3, 4, where

A =

1 1

−1 1

and the vectors b

are (0, 0),(1, 0), (0, 1) and (1, 1).

(a) Show that the ﬁxed points of the T

’s form the vertices of a square S.

(b) Compute T S and T

D. (a) Find an IFS on R that generates the Cantor set.

HINT: Identify two self maps of C with disjoint union equal to C.

(b) Find a different IFS that also generates C.

E. Consider the maps T = {T

, T

} given by

.8 .0

0 .8

¸·

.04

.5 0

0 .5

¸·

.25

.35 −.35

.35 .35

¸·

.27

.08

.35 .35

−.35 .35

¸·

.38

.43

11.7 Iterated Function Systems 385

(a) Use a computer to plot the maple leaf pattern A ﬁxed by T .

(b) Plot T

A for 1 ≤ i ≤ 4 to see the self-symmetries.

F. (a) Show that an isometry T with T 0 = 0 is linear.

(b) Show that every similitude T of R

has the form T x = rUx + a, where r > 0,

a ∈ R

, and U is a unitary matrix.

HINT: Set g(x) = r

−1

(T x −T 0). Verify that g is isometric and apply (a).

G. The fractal dimension of a bounded subset A of R

is computed by counting, for

ε > 0, the smallest number of cubes of side length ε that cover A, call it N(A, ε). The

fractal dimension is then the limit lim

ε→0

logN(A, ε)

logε

−1

, if it exists.

(a) Compute the fractal dimension of the unit n-cube in R

(b) Show that the fractal dimension is not affected by scaling.

has interior, show that the fractal dimension is n.

(d) Compute the fractal dimension of the Cantor set C.

(e) Compute the fractal dimension of the Sierpinski snowﬂake.

CHAPTER 12

Differential Equations

In this chapter, we apply analysis to the study of ordinary differential equations,

generally called DEs or ODEs. Ordinary is used to indicate differential equations

of a single variable, in contrast with partial differential equations (PDEs), where

several variables, and hence partial derivatives, appear. We will see some PDEs in

the chapters on Fourier series, Chapters 13 and 14.

Most introductory courses on differential equations present methods for solving

DEs of various special types. We will not be concerned with those techniques

here except to give a few pertinent examples. Rather we are concerned with why

differential equations have solutions, and why these solutions are or are not unique.

This topic, crucial to a full understanding of differential equations, is often omitted

from introductary courses because it requires the tools of real analysis.

12.1. Integral Equations and Contractions

We consider an example that motivates the approach of the next section. Start

with an initial value problem, which consists of two parts:

(x) = ϕ(x, f (x)) for a ≤ x ≤ b

f(c) = y

The ﬁrst equation is the DE and the second is an initial value condition. The func-

tion ϕ(x, y) is a continuous function of two variables deﬁned on [a, b] × R and

c is a given point in [a, b]. By solving the DE or, equivalently, solving the initial

value problem, we mean ﬁnding a function f (x) that is deﬁned and differentiable

on the interval [a, b] and satisﬁes both the differential equation and the initial value

condition.

This DE is of ﬁrst order, as the equation involves only the ﬁrst derivative. In

general, the order of a differential equation is the highest-order derivative of the

unknown function that appears in the equation.

Because of the subject’s connections to physics, chemistry, and engineering, it

is common in differential equations to suppress the dependence of the function f

on x [i.e., to write f instead of f(x)]. Typically in the sciences, each variable has

386

12.1 Integral Equations and Contractions 387

a physical signiﬁcance, and it can be a matter of choice about which is the inde-

pendent variable and which is dependent. We will sometimes do this in examples,

where simplifying otherwise complicated expressions seems to be worth the extra

demands this notation makes.

Our ﬁrst step is to turn this problem into a ﬁxed-point problem by integration.

Indeed, from the fundamental theorem of calculus, our solution must satisfy

f(x) = f(c) +

(t) dt = y

ϕ(t, f(t)) dt.

Conversely, a continuous solution of this integral equation is automatically differ-

entiable by the Fundamental Theorem of Calculus, and

(x) =

ϕ(t, f(t)) dt

= ϕ(x, f (x))

and

f(c) = y

ϕ(t, f(t)) dt = y

Thus f satisﬁes the DE, including the initial value condition.

This integral equation suggests studying a map from C[a, b] into itself deﬁned

T f(x) = y

ϕ(t, f(t)) dt.

The solutions to the integral equation, if any, correspond precisely to the ﬁxed

points of T . The Contraction Principle (11.1.6) is well suited to this kind of prob-

lem. There are also more sophisticated approaches that give weaker conclusions

from weaker hypotheses. However, the Contraction Principle gives both existence

and uniqueness of a solution, when it can be applied. Consider the following spe-

ciﬁc example.

12.1.1. EXAMPLE. We will solve the initial value problem

(x) = 1 + x − f(x) for −

≤ x ≤

f(0) = 1.

First convert it to the integral equation

f(x) = 1 +

1 + t − f(t) dt

= 1 + x +

−

f(t) dt

for f in C[−

Deﬁne a map T on C[−

] by sending f to the function T f given by

T f(x) = 1 + x +

−

f(t) dt.

The solution of the integral equation is a ﬁxed point of T .

388 Differential Equations

To use the Banach Contraction Principle, we must show that T is a contraction.

We have

|T f(x) − T g(x)| =

f(t) − g(t) dt

≤

|f(t) − g(t)|dt

≤

kf − gk

∞

= kf − gk

∞

|x|

dt ≤

kf − gk

∞

This estimate is independent of x in [−

], and thus we obtain

kT f − T gk

∞

≤

kf − gk

∞

Hence T is a contraction.

By the Contraction Principle (11.1.6), there is a unique ﬁxed point f

∞

that will

solve our DE. Moreover, any sequence of functions (f

) with f

n+1

= T f

will

converge to f

∞

in C[−

]. For example, let us take f

to be the constant function

1. Then

(x) = T f

(x) = 1 + x +

−

1dt = 1 +

Similarly,

(x) = T f

(x) = 1 + x +

−

1 +

= 1 +

−

And

(x) = T f

(x) = 1 + x +

−

1 +

−

= 1 +

−

In general, we can establish by induction (do it yourself!) that

(x) = 1 +

−

+ ··· +

(n+1)!

(−x)

n+1

This sequence evidently consists of the partial sums of an inﬁnite series. The new

term added at the nth stage is

(n+1)!

(−x)

n+1

, which on [−

] has max norm

max

|x|≤1/2

(−x)

n+1

(n + 1)!

n+1

(n + 1)!

−1

Therefore, this power series converges uniformly on [−

] by the Weierstrass M -

test. Figure 12.1 gives the graphs of f

, f

, and f

∞

on [−1, 1]. The astute reader

should notice that these are the Taylor polynomials for e

−x

except that the term in

x is missing.

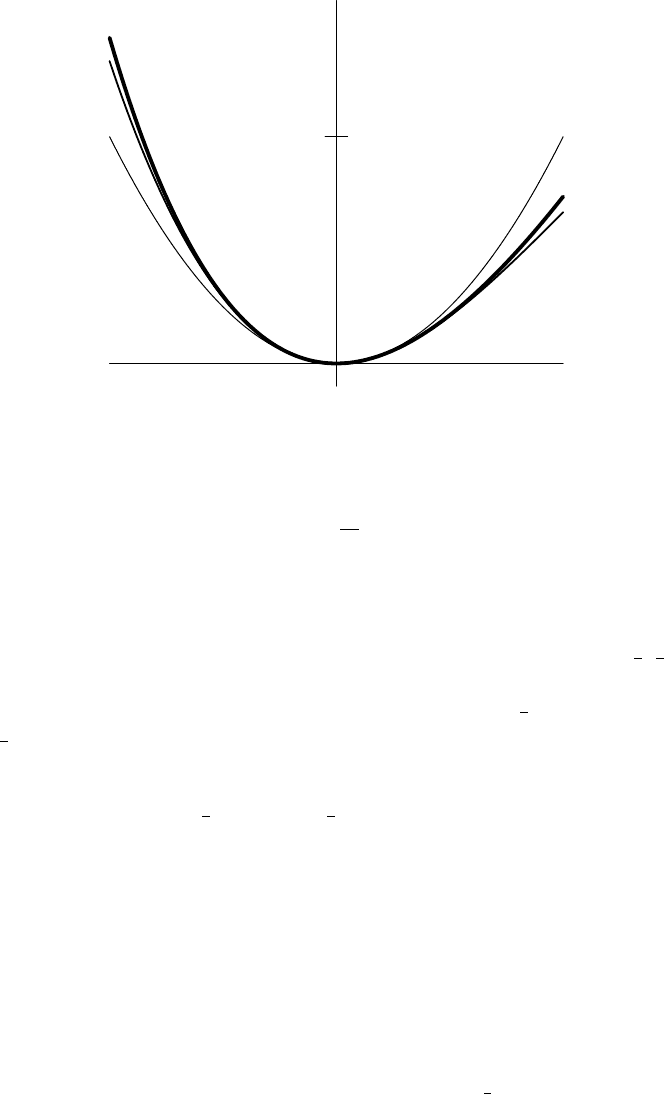
12.1 Integral Equations and Contractions 389

1.5

∞

FIGURE 12.1. The ﬁrst three approximants and f

∞

on [−1, 1].

We obtain

∞

(x) = x +

∞

k=0

(−x)

= e

−x

+ x.

This shows that e

−x

+ x is the unique solution to our integral equation. Indeed,

−x

+ x)

= −e

−x

+ 1 = 1 + x − (e

−x

+ x) and e

−0

+ 0 = 1.

Now the reader may notice that we only found a solution valid on [−

], but

in fact f

∞

(x) = e

−x

+ x is a valid solution on all of R. One way we can deal with

this is to reconsider our problem beginning at the point x =

, and try to extend to

[

, 1]. We have the DE

(x) = 1 + x − f(x) for 0 ≤ x ≤ 1

) = e

−1/2

−

The exact same argument on this new interval will yield the unique attractive ﬁxed

point f

∞

(x) = e

−x

+ x valid on [0, 1]. It is then easy to see that we can bootstrap

our way to the unique solution on the whole line.

In the next two sections, we show how the solutions to a largefamily of DEs can

formulated as ﬁxed-point problems. Then we may use the Contraction Principle to

show that these DEs always have solutions.

Exercises for Section 12.1

A. Use the method of this section to solve f

(x) = 1 +

f(x) for 0 ≤ x ≤ 1 and

f(0) = 1. You should be able to recognize the series and successfully ﬁnd a closed

form for the solution. Show that, in fact, this solution is valid for all real numbers.

390 Differential Equations

B. For b > 0 and a ∈ R, deﬁne T on C[0, b] by T f(x) = a +

f(t)xe

−xt

dt. Prove

that T is a contraction. Hence show that the integral equation

f(x) = a +

f(t)xe

−xt

dt has a unique solution f ∈ C[0, ∞).

C. Consider the DE f

(x) =

−2

f(x) and f(1) = 1 for

≤ x ≤

(a) Prove that the associated integral map is a contraction mapping.

(b) Look for a solution to the DE of the form f (x) = ax

= 1, ﬁnd a formula for f

= T

. Express this as a familiar

power series of logx, and hence evaluate it.

HINT: Use the closed form of the solution from (b) to guide you.

D. Consider the DE y

= 1 + y

and y(0) = 0.

(a) Solve the DE directly.

(b) Show that the associated integral map T is not a contraction mapping on C[−r, r]

for any r > 0.

mapping on this ball.

(d) Hence show that there is a unique solution on [−r, r].

E. Consider a ball falling to the ground. The downward force of gravity is counteracted

by air resistance proportional to the velocity. Find a formula for the velocity of the ball

if it is at rest at time 0 [i.e., v(0) = 0] as follows:

(a) Show that the velocity satisﬁes v

(t) = g − cv(t), where g is the gravity constant

and c is the constant of air resistance. What is the initial condition?

(b) Construct the associated integral map T . Starting with v

(t) = 0, iterate T and

obtain a formula for the solution v

∞

Compute lim

t→∞

∞

(t). This is known as the terminal velocity.

12.2. Calculus of Vector-Valued Functions

In this section, we develop differentiation and integration for vector-valued

functions. We will need this material in the next section, to convert an nth-order

DE for a real-valued function into a ﬁrst-order DE for a vector-valued function.

Consider a function f : [a, b] → R

, where f(x) = (f

(x), f

(x), . . . , f

(x))

and each coordinate function f

maps [a, b] to R. Although much of this is done

by looking at the coordinate functions, there are some crucial differences between

and R. Most notably, we do not have a total order in R

, so we cannot take the

supremum or inﬁmum of the set f([a, b]) ⊂ R

12.2.1. DEFINITION. We say that a vector-valued function f : [a, b] → R

differentiable at a point x

∈ (a, b) if

lim

h→0

f(x

+ h) − f(x

)

12.2 Calculus of Vector-Valued Functions 391

exists in R

. As usual, we write f

) for the limit and call it the derivative of

f at x

. Notice that the numerator is in R

while the denominator is a scalar, so

) is in R

We can deﬁne left differentiable and right differentiable in the natural way,

and we say f is differentiable on the interval [a, b] if it is differentiable at every

point of (a, b) in the sense just stated and left or right differentiable at the endpoints.

We leave it for the reader to verify that if f : [a, b] → R is differentiable at

∈ [a, b], then f is continuous at x

12.2.2. PROPOSITION. Suppose that f : [a, b] → R

given by f(x) =

(x), . . . , f

(x)), where each f

maps [a, b] into R. Then f is differentiable

at x

∈ [a, b] if and only if each f

is differentiable at x

. Moreover, f

) =

), . . . , f

)).

PROOF. Fix x

∈ [a, b] and consider the function

g(h) =

f(x

+ h) − f(x

)

deﬁned for those h so that x

+ h ∈ [a, b]. If g(h) = (g

(h), . . . , g

(h)), then we

have that g

(h) = (f

+ h) − f

))/h for each i. Thus f is differentiable x

if and only if the limit of g(h) exists as h → 0 and each f

is differentiable at x

if and only if the limit of g

(h) exists as h → 0. So it sufﬁces to show that the

limit of g(h) exists and equals (u

, . . . , u

) if and only if the limits of each of its

components g

exists and equals u

. But this is established in Exercise 5.3.D. ¥

We leave it to the reader to verify that sums and scalar multiples of differ-

entiable functions are differentiable. Since products of real-valued differentiable

functions are differentiable, it follows easily from the previous theorem that if f

and g are vector-valued differentiable functions, then f · g is differentiable. Notice

that f · g is real valued.

On the other hand, not all results carry over from the real-valued setting. For

example, consider the function f : [0, 2π] → R

given by f(x) = (cosx, sinx).

It is easy to see that f(2π) = f(0), but there is no x ∈ [0, 2π] so that f

(x) is the

zero vector. However, we do have the following result. The analaguous fact for

real-valued functions is a corollary of the Mean Value Theorem.

12.2.3. THEOREM. Suppose that f : [a, b] → R

is continuous on [a, b] and

differentiable on (a, b). Then there is c ∈ (a, b) so that

kf(b) − f(a)k ≤ (b − a)kf

(c)k.

PROOF. Deﬁne v = f(b) −f (a) and a function g : [a, b] → R by g(x) = v ·f(x).

Notice that if v is the zero vector, then we are done. So we may assume kvk 6= 0.

A brief calculation shows that g is differentiable and

(x) = v · f

(x).

392 Differential Equations

Applying the Mean Value Theorem to g shows that there is c ∈ (a, b) so that

g(b) − g(a) = (b − a)

v · f

(c)

Using the deﬁnition of g and rearranging shows that g(b) − g(a) = kvk

. The

Schwarz inequality now gives

kvk

= (b − a)v · f

(c)k.

Dividing by the nonzero quantity kvk gives the inequality. ¥

12.2.4. COROLLARY. For a function f : [a, b] → R

that is C

on [a, b], we

have kf(b) − f(a)k ≤ (b − a)kf

∞

Next, we develop integration for vector-valued functions. Following the nota-

tion of Section 6.3, given P = {x

< . . . < x

}, a partition of [a, b], and a set of

points X = {x

: 1 ≤ j ≤ n} with x

∈ [x

j−1

, x

], deﬁne the Riemann sum

I(f, P, X) =

j=1

f(x

)∆

where the vector f(x

) is multiplied by the the scalar ∆

= x

−x

j−1

. We say that

the set of points X is subordinate to the partition P .

12.2.5. LEMMA. Given a function f : [a, b] → R

with f = (f

, . . . , f

), a

partition P of [a, b], and a set of points X subordinate to P , we have

I(f, P, X) =

I(f

, P, X), I(f

, P, X), . . . , I(f

, P, X)

We leave the proof as an exercise. The next deﬁnition says, in essence, that a

function is integrable provided the Riemann sums “eventually” converge. However,

making this precise requires several quantiﬁers. You should compare this deﬁnition

to Theorem 6.3.8.

12.2.6. DEFINITION. We say a bounded function f : [a, b] → R

is Riemann

integrable if there is a vector, v, so that for every ε > 0, there is a δ > 0 so

that every partition Q of [a, b] with mesh(Q) < δ and every choice of points X

subordinate to Q,

I(f, Q, X) − v

< ε.

As usual, we denote v by

f(x) dx.

Theorem 6.3.8 shows that this deﬁnition agrees with our previous deﬁnition of

Riemann integrable function if n = 1.