Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


11.1 Fixed Points and the Contraction Principle 343
This formula (I −A)
−1
=
∞
P
k=0
A
k
should be seen as parallel to the power series
identity
1
1 − x
=
∞
X
k=0
x
k
for |x| < 1.
The condition |x| < 1 guarantees that the series converges. The same role is played
for matrices by the contractive condition (11.1.11).
Exercises for Section 11.1
A. Let T x = 1.8(x − x
3
). Find the smallest real number R so that lim
n→∞
|T
n
x| = +∞
for all |x| > R.
B. Show that T x = sin x is not a contraction on [−1, 1].
C. Give an example of a differentiable map T from R to R whose fixed points are exactly
the set of integers. Find points where |T
0
(x)| > 1.
D. Explain why, in the previous example, points with |T
0
(x)| > 1 necessarily exist.
E. Suppose that S and T are contractions with Lipschitz constants s and t, respectively.
Prove that the composition ST is a contraction with Lipschitz constant st.
F. Consider a case of Example 11.1.11 for A =
·
.5 .4
0 .8
¸
and b =
·
.1
.2
¸
. Explicitly
compute the infinite sum
∞
P
k=0
A
k
in order to solve for the fixed point of T x = Ax + b.
G. Redo Example 11.1.11 using the 1-norm kxk
1
=
n
P
i=1
|x
i
| on R
n
in place of kxk
∞
.
HINT: Show that T is a contraction if and only if max
1≤j≤n
n
P
i=1
|a
ij
| < 1.
H. Define T on C[−1, 1] by T f(x) = f (x) +
x
2
− f(x)
2
2
. Set f
0
= 0 and f
n+1
= Tf
n
for n ≥ 0. Prove that f
n
is a monotone increasing sequence of functions such that
0 ≤ x
2
− f
n+1
(x)
2
≤ (1 −
1
4
x
2
)(x
2
− f
n
(x)
2
).
Hence show that f
n
is a sequence of polynomials converging uniformly to |x|.
I. Define a map D on C[0, 1] as follows:
Df(x) =
2
3
+
1
3
f(3x) for 0 ≤ x ≤
1
3
(2 + f(1))(
2
3
− x) for
1
3
≤ x ≤
2
3
x −
2
3
for
2
3
≤ x ≤ 1.
(a) Sketch the graph of some function f and Df .
(b) Show that D is a contraction.
(c) Describe the fixed point. HINT: Repeatedly apply D to the function f(x) = 1/3

344 Discrete Dynamical Systems
J. Suppose that S and T are contractions on X with Lipschitz constant c < 1 and fixed
points x
s
and x
t
respectively. Prove that kx
s
− x
t
k ≤ (1 − c)
−1
kS − T k
∞
, where
kS − T k
∞
= sup
x∈X
kSx − T xk.
HINT: Estimate kx
s
− x
t
k in terms of kx
s
− T x
s
k.
K. Suppose that for 0 ≤ s ≤ 1, T
s
is a contraction of a complete normed space X
with Lipschitz constant c < 1. Moreover, assume that this is a continuous path of
contractions. That is, lim
s→s
0
kT
s
−T
s
0
k
∞
= 0. Prove that the fixed points x
s
of T
s
form
a continuous path.
HINT: Use the previous exercise.
11.2. Newton’s Method
Newton’s method is an iterative method for rapidly computing the zeros of dif-
ferentiable functions. The Contraction Principle gives a nice proof that this method
works.
Suppose we have a function f on R and a reasonable guess x
0
for the zero (or
root) of f. If f is differentiable at x
0
, then we can draw the tangent line at x
0
. It
seems plausible that if x
0
is close to the root of the function, the root of the tangent
line will be even closer. This uses one of the basic ideas of Differential Calculus:
The tangent line to f at x
0
is a good approximation to f near x
0
.
The equation of the tangent line is
y = f (x
0
) + f
0
(x
0
)(x − x
0
).
To find the root, we set y = 0 and solve for x, to obtain
x = x
0
−
f(x
0
)
f
0
(x
0
)
.
Call this root x
1
. By repeating the same calculation for x
1
, we obtain a sequence
(x
n
)
∞
n=1
, where
x
n+1
= x
n
−
f(x
n
)
f
0
(x
n
)
for n ≥ 1.
Our hope is that the sequence converges to a point x
∗
satisfying f(x
∗
) = 0. See
Figure 11.4 for an example of (the first few terms) of such a sequence.
To prove this, we reformulate the problem using fixed points. Suppose f(x) is
twice differentiable and f(x
∗
) = 0 for some point x
∗
. Define a dynamical system
T by
T x = x −
f(x)
f
0
(x)
.
It is easy to see that if f(x
∗
) = 0, then T x
∗
= x
∗
and vice versa. So we are looking
for a fixed point for the function T . Notice that for this definition to make sense,
we require f
0
(x) 6= 0 on our domain. This will show up in our hypotheses as the
condition f
0
(x
∗
) 6= 0.
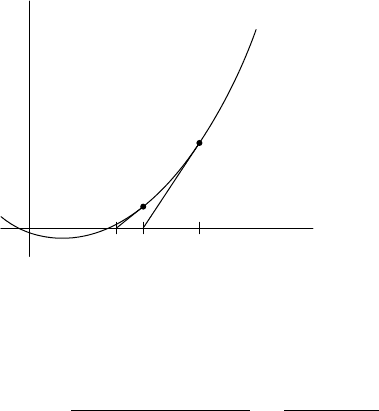
11.2 Newton’s Method 345
x
y
y = f(x)
x
0
x
1
x
2
FIGURE 11.4. Example of a function f and sequence (x
n
).
We compute the derivative
T
0
(x) = 1 −
f
0
(x)
2
− f(x)f
00
(x)
f
0
(x)
2
=
f(x)f
00
(x)
f
0
(x)
2
.
Notice that T
0
(x
∗
) = 0. So x
∗
is an attractive fixed point by Lemma 11.1.2. More-
over, the constant c used may be any small positive number. Indeed, the closer we
get to x
∗
, the smaller the value of c that may be used. This will be important in
obtaining very rapid convergence.
In addition to verifying that Newton’s method works, we can estimate how
quickly the error decreases. This kind of error analysis is fundamental to deciding
the effectiveness of an algorithm. It is considered minimally acceptable if the error
tends to zero geometrically in the sense that
|x
n+1
− x
∗
| ≤ c|x
n
− x
∗
| for n ≥ N
for some constant c < 1. For if c
s
< .1, we obtain an additional digit of accuracy
every s iterations. Compare Example 11.1.8.
However, if great accuracy is desired, this is not all that fast. Some algorithms,
such as Newton’s method, converge quadratically, meaning that there is a constant
M so that
|x
n+1
− x
∗
| ≤ M |x
n
− x
∗
|
2
for n ≥ N.
Once |x
n
− x
∗
| < .1/M, the number of digits of accuracy doubles every iteration.
Thus, once we get sufficiently close to the solution, the sequence approaches x
∗
very rapidly.
11.2.1. NEWTON’S METHOD.
Suppose that f is twice continuously differentiable, and there is a point x
∗
∈ R
such that f (x
∗
) = 0 and f
0
(x
∗
) 6= 0. There is an r > 0 so that if x
0
belongs
to [x
∗
− r, x
∗
+ r], then the iterates x
n+1
= x
n
− f(x
n
)/f
0
(x
n
) converge to x
∗
.
Moreover, there is a constant M such that
|x
n+1
− x
∗
| < M |x
n
− x
∗
|
2
for n ≥ 1;
so the iterates converge quadratically.

346 Discrete Dynamical Systems
PROOF. Let T x = x − f(x)/f
0
(x). Then T x
∗
= x
∗
. As computed previously,
T
0
(x) =
f(x)f
00
(x)
f
0
(x)
2
.
In particular, T
0
(x
∗
) = 0. Also, T
0
(x) is defined for x near x
∗
since f
0
(x) 6= 0
for x near x
∗
. Choose r > 0 sufficiently small so that |T
0
(x)| ≤
1
2
on the interval
[x
∗
−r, x
∗
+r]. By Lemma 11.1.2, for any x
0
in this range, the iterates x
n+1
= T x
n
converge to x
∗
, and
|x
n
− x
∗
| ≤ 2
−n
|x
0
− x
∗
| ≤ 2
1−n
|x
0
− x
1
|.
In particular, x
n
converge at least geometrically to the fixed point, and each x
n+1
is closer to this point than x
n
.
Quadratic convergence is a consequence of using the Mean Value Theorem
in a more precise way. The estimate from Lemma 11.1.2 only used the fact that
|T
0
(x)| ≤ c near the fixed point x
∗
. We will exploit the fact that T
0
(x
∗
) = 0. Here
are the details. Let
A = sup
|x−x
∗
|≤r
|f
00
(x)| and B = inf
|x−x
∗
|≤r
|f
0
(x)|,
and set M = A/B. By the Mean Value Theorem, there is a point a
n
between x
n
and x
∗
such that
f(x
n
) = f (x
n
) − f (x
∗
) = f
0
(a
n
)(x
n
− x
∗
).
Solve for x
n
− x
∗
and substitute into the following:
x
n+1
− x
∗
= (x
n
− x
∗
) + (x
n+1
− x
n
)
=
f(x
n
)
f
0
(a
n
)
−
f(x
n
)
f
0
(x
n
)
=
f(x
n
)
f
0
(a
n
)f
0
(x
n
)
¡
f
0
(x
n
) − f
0
(a
n
)
¢
=
x
n
− x
∗
f
0
(x
n
)
¡
f
0
(x
n
) − f
0
(a
n
)
¢
.
Applying the Mean Value Theorem again, this time to f
0
, provides a point b
n
be-
tween x
n
and a
n
such that
|f
0
(x
n
) − f
0
(a
n
)| = |f
00
(b
n
)(x
n
− a
n
)| ≤ A|x
n
− x
∗
|.
Combining this with |f
0
(x
n
)| ≥ B and substituting again yields
|x
n+1
− x
∗
| ≤
|x
n
− x
∗
|
B
A|x
n
− x
∗
| = M |x
n
− x
∗
|
2
.
This establishes the quadratic convergence. ¥
11.2.2. EXAMPLE. COMPUTATION OF SQUARE ROOTS. A long time ago in
places far far away, everyone had to compute square roots by hand. Today, a few
people have to program calculators to compute them. Newton’s method is an ex-
cellent way for a person or a computer to find square roots rapidly to high accuracy.
11.2 Newton’s Method 347
To illustrate the value of the method and of quadratic convergence, we’ll compute
a few square roots. Unlike a calculator, we also give an upper bound for the error
between our computed value and the true value.
Finding the square root of a > 0 means finding the positive root of the function
f(x) = x
2
− a. Applying Newton’s method, a simple computation gives
T x = x −
x
2
− a
2x
=
1
2
³
x +
a
x
´
.
In fact, we will see that any initial positive choice of x
1
will converge to
√
a. Try
this on your calculator as a method of computing
√
2 or
√
71.
Suppose that you are asked to compute
√
149 to 20 digits of accuracy. Since
12
2
= 144 < 149 < 169 = 13
2
, let x
0
= 12 be our first approximation. Clearly,
the error is at most .5. Moreover,
T
0
(x) =
1
2
³
1 −
149
x
2
´
.
This is evidently monotone. Thus on [12, 13], the derivative is bounded by
max
©
|T
0
(12)|, |T
0
(13)|
ª
= max
n
5
288
,
10
169
o
=
10
169
< .06.
Therefore, Newton’s method guarantees that the sequence
x
0
= 12, x
n+1
=
1
2
³
x
n
+
149
x
n
´
for n ≥ 0
converges quadratically to
√
149.
Let us compute the other constants involved. As f
0
(x) = 2x and f
00
(x) = 2,
we obtain
A = sup
12≤x≤13
|f
00
(x)| = 2
B = inf
12≤x≤13
|f
0
(x)| = 24
M =
A
B
< .084.
Again using the Mean Value Theorem, note that
|f(x
0
)| = |f (x
0
) − f (x
∗
)| = |f
0
(c)||x
0
− x
∗
| ≥ B|x
0
− x
∗
|.
Thus
|x
0
− x
∗
| < |f (x
0
)|/24 = 5/24 < .21.
From the error estimate for Newton’s method, we obtain
|x
n+1
− x
∗
| ≤ .084|x
n
− x
∗
|
2
.
Starting with x
0
= 12, we have the following table of terms and bounds on the
error.
348 Discrete Dynamical Systems
n x
n
Bound on |x
n
− x
∗
|
0 12 .21
1 12.2083 3.704 × 10
−3
2
12.206555745165 1.153 × 10
−6
3
12.2065556157337036 3.572 ×10
−13
4
12.20655561573370295189 1.117 × 10
−26
5
12.20655561573370295189 1.048 × 10
−53
We already have 20 digits of accuracy at n = 4. In fact, to progress further,
we need to worry more about the round-off error of our calculations than with
Newton’s method.
Look at the global aspects of this example. It is easy to see from the graph that
f(x) = x
2
− 149 is concave, much like Figure 11.4. If x
0
lies in (0,
√
149), then
x
1
>
√
149. However, taking x
0
very small will result in a huge second term. After
that, it is also apparent from the graph that x
n
decreases monotonely and quickly to
√
149. Similarly, starting with x
0
< 0, the same procedure follows from reflection
of the whole picture in the y-axis—the sequence converges rapidly to −
√
149. The
point x
0
= 0 is a nonstarter because f
0
(0) = 0.
Exercises for Section 11.2
A. Show that f(x) = x
3
+ x + 1 has exactly one real root. Use Newton’s method to
approximate it to eight decimal places. Show your error estimates.
B. The equation sinx = x/2 has exactly one positive solution. Use Newton’s method to
approximate it to eight decimal places. Show your error estimates.
C. (a) Set up Newton’s method for computing cube roots.
(b) Show by hand that
3
√
2 − 1.25 < .01.
(c) Compute
3
√
2 to eight decimal places.
D. Let f(x) = (
√
2)
x
for x ∈ R. Sketch y = f(x) and y = x on the same graph. Given
x
0
∈ R, we define a sequence by x
n+1
= f(x
n
) for n ≥ 0.
(a) Find all fixed points of f.
(b) Show that the sequence (x
n
)
∞
n=1
is monotone.
(c) If x
∗
= lim
n→∞
x
n
exists, prove that f(x
∗
) = x
∗
.
(d) For which x
0
∈ R does the sequence (x
n
) converge, and what is the limit?
E. Find the largest critical point of f(x) = x
2
sin(1/x) to four decimal places.
F. Find the minimum value of f(x) = (logx)
2
+ x on (0, ∞) to four decimal places.
G. Apply Newton’s method to find the root of f(x) = (x − r)
1/3
. Start with any point
x
0
6= r, and compute |x
n
− r|. Explain what went wrong here.
11.3 Orbits of a Dynamical System 349
H. Modified Newton’s method. With the same setup as for Newton’s method, show that
the sequence x
n+1
= x
n
−
f(x
n
)
f
0
(x
0
)
for n ≥ 0 converges to x
∗
.
I. (a) Let a > 0. Show that Newton’s formula for solving xa = 1 yields the iteration
x
n+1
= 2x
n
− ax
2
n
.
(b) Suppose that x
0
=
1 − ε
a
for some |ε| < 1. Derive the formula for x
n
.
(c) Do the same analysis for the iteration scheme x
n+1
= x
n
(3 − ax
n
− (ax
n
)
2
).
Explain why this is a superior algorithm.
J. Let h(x) = x
1/3
e
−x
2
.
(a) Set up Newton’s method for this function.
(b) If 0 < |x
n
| < 1/
√
6, then |x
n+1
| > 2|x
n
|.
(c) Show that if x
n
> 1/
√
6, then x
n
< x
n+1
< x
n
+
1
2x
n
.
(d) Hence show that Newton’s method never works unless x
0
= 0. However, given
ε > 0, there will be an N so large that |x
n+1
− x
n
| < ε for n ≥ N.
(e) Sketch h and try to explain this nasty behaviour.
K. Three towns, Alphaville, Betatown, and Gammalot, are situated around the shore of a
circular lake of radius 1 km. The largest town Alphaville claims one half of the area of
the lake as its territory. The town mathematician is charged with computing the radius
r of a circle from the town hall (which is right on the shore) that will cut off half the
area of the lake. Compute r to seven decimal places.
HINTS: Let T denote the town hall, and O the centre of the lake. The circle of radius
r meets the shoreline at X and Y . The area enclosed is the union of two segments of
circles cut off by the chord XY . Express r and the area A as functions of the angle
θ = ∠OT X.
MORE HINTS: (1) Show that (i) 1 < r < 2; (ii) ∠T OX = π − 2θ; (iii) the area
of the segment of a circle of radius ρ cut off by a chord that subtends an angle α is
ρ
2
(α −sinα)/2. (2) Show that r = 2cos θ and A(θ) = 2π −4θ sin
2
θ −2sin(2θ). (3)
Solve A(θ) = π using Newton’s method. Show error estimates.
11.3. Orbits of a Dynamical System
There are several possibilities for the structure of the orbit of a point x
0
. Fixed
points, which we’ve discussed in detail, have the simplest possible orbits, namely
O(x
0
) = {x
0
}. Almost as good as fixed points from the point of view of dynamics,
and certainly more common, are periodic points. We say that x
∗
is a periodicpoint
if there is a positive integer n such that T
n
x
∗
= x
∗
. The smallest positive n for
which this holds is called the period. Notice that x
∗
is a fixed point of T
n
. We can
therefore call x
∗
an attractive periodic point or a repelling periodic point for T
if it is an attractive or repelling fixed point of T
n
. Because T maps an open set
around x
∗
to an open set around T x
∗
, it is easy to check that points in the same
periodic orbit are either all attractive or all repelling.
Let us discuss the terminology of dynamical systems by examining a particular
map, namely the map T x = 1.8(x − x
3
) that we discussed in Section 11.1. Our
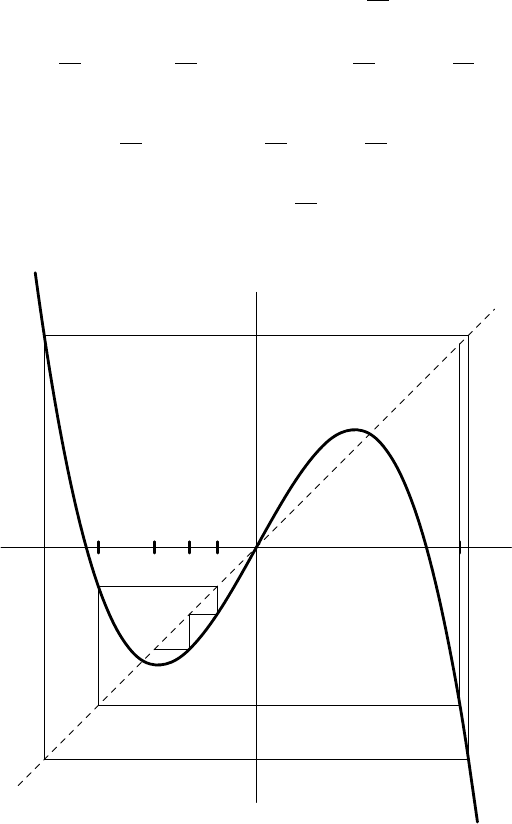
350 Discrete Dynamical Systems
example contains an orbit of period 2, namely {±
√
14/3}. Indeed, it is an easy
calculation to see that
T (
√
14/3) = −
√
14/3 and T (−
√
14/3) =
√
14/3.
See Figure 11.5. This is a repelling orbit since
(T
2
)
0
(
√
14/3) = T
0
(T
√
14/3)T
0
(
√
14/3)
= (1.8 − 5.4
14
3
)
2
= 547.56 > 1.
x
y
x
0
x
1
x
2
x
3
x
4
FIGURE 11.5. Graph of T x = 1.8(x−x
3
) showing period 2 orbit
and a nearby orbit.
A point x is called an eventually periodic point if T
n
x eventually belongs to
a period. Consider our example again. Notice that T (1) = 0. So T
n
(1) = 0 for all
n ≥ 1. The equation T x = 1 has a solution that is the root of the cubic
1 = 1.8x − 1.8x
3
.
This has a solution r since every real polynomial of odd degree has a root by Ex-
ercise 5.6.D and we may calculate r ≈ −1.20822631883. Then with x
0
= r, we
obtain x
1
= T x
0
= 1 and x
2
= T (1) = 0, and so x
0
= T
n
x
0
= 0 for all n ≥ 2.
Similarly, we have a sequence (r
n
) of points so that T
n
(r
n
) = 0, such as r
0
= 0,
11.3 Orbits of a Dynamical System 351
r
1
= 1, r
2
≈ −1.20823, r
3
≈ 1.24128. Observe that r
n
is close to (−1)
n−1
√
14/3
for large n, in the sense that r
n
− (−1)
n−1
√
14/3 converges to zero.
Likewise there are points that are eventually mapped onto the two attractive
fixed points ±
2
3
.
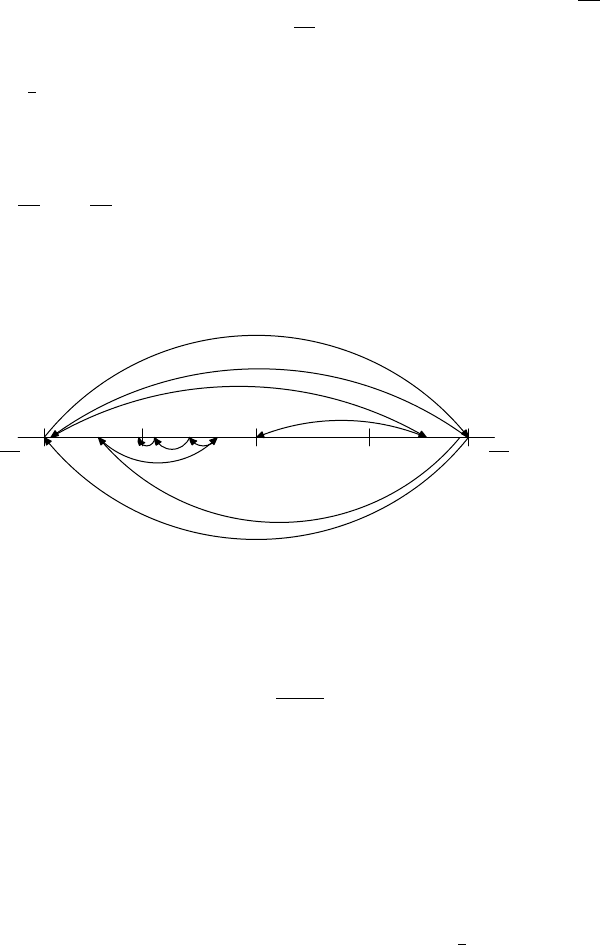
Figure 11.6, called a phase portrait, attempts to show graphically the be-
haviour of our mapping T . Rather than using a graph, it represents the space as
a line and the function as arrows taking a point x to T x. In particular, you should
observe that except for a sequence of points that eventually map to 0, every other
point in (−
√
14/3,
√
14/3) has an orbit that converges to one of the two attractive
fixed points ±2/3. Notice that, except for the two arrows for the period 2 orbit,
arrows above the line show the first few terms of the sequence (r
n
) mentioned
previously, while those below the line show the “nearby” orbit from Figure 11.5.
0
√
14/3−
√
14/3
2/3
−2/3
FIGURE 11.6. Phase portrait of T x = 1.8(x − x
3
)
.
Of course, this example does not exhaust the possibilities for the behaviour of
an orbit. It can happen that the orbit of a single point is dense in the whole space.
A point x is called a transitive point if O(x) = X. The following examples
are more complicated than our first one and exhibit this new possibility as well as
having many periodic points.
11.3.1. EXAMPLE. Let the space be the unit circle T. We can describe a typical
point on the circle by the angle θ it makes to the positive real axis in radians. If
θ is changed to θ + 2nπ, the point determined remains the same. So this angle is
determined “up to a multiple of 2π.” We may add two angles, or multiply them
by an integer. The resulting point does not depend on how we initially measure
the angle. (Notice that when multiplying by a fraction such as
1
2
, the answer does
depend on which way the angle is represented. Half of 1 does not determine the
same point as half of 1 + 2π.) We call this arithmetic modulo 2π. We will write
θ ≡ ϕ (mod 2π)
to mean that θ−ϕ is an integer multiple of 2π, which is to say that θ and ϕ represent
the same point on the circle. In this way, we may think of the unit circle T as the
real line wrapping around the circle infinitely often, meeting up at the same point
every 2π. This will be convenient for calculation.

352 Discrete Dynamical Systems
Consider the rotation map R
α
through an angle α given by
R
α
θ ≡ θ + α (mod 2π).
It is rather easy to analyze what happens here. The only way to obtain a periodic
point is to have
θ ≡ R
n
α
θ = θ + nα (mod 2π).
This requires nα to be an integer multiple of 2π. When this occurs and n is as
small as possible, it follows that every point in T has period n. Indeed, R
n
α
= id,
the identity map. This is the case for those α that are a rational multiple of 2π.
Equivalently, R
α
is periodic if and only if α/2π ∈ Q.
On the other hand, for all irrational values of α/2π, R
α
has no periodic points.
We will show that the orbit of every point is dense in the circle. Indeed, suppose
that ε > 0 and that θ and ϕ are two points on the circle. We wish to find an integer
n so that |R
n
α
θ − ϕ| < ε.
To do this, we first solve a simpler problem. We will find a positive integer m
so that |R
m
α
0| < ε. This says that, while there are no periodic points, points do
come back very close to where they start every once in a while. Our method uses
the pigeonhole principle.
Pick an integer N so large that 2π < Nε. Divide the circle into N intervals
I
k
=
£
(k−1)2π
N
,
k2π
N
¢
for 1 ≤ k ≤ N . Note that each interval has length
2π
N
< ε.
Now consider the N + 1 points
{x
j
≡ R
j
α
0 = jα (mod 2π) : 0 ≤ j ≤ N}.
These N + 1 points are distributed in some way among the N intervals I
k
. As there
are more points than intervals, the pigeonhole principle merely asserts that some
interval contains at least two points. Let i < j be two integers in our set so that x
i
and x
j
both lie in some interval I
k
. These two points are therefore close to each
other. Precisely,
|x
j
− x
i
| <
2π
N
< ε.
Now we use the fact that R
α
is isometric, meaning that
|R
α
θ − R
α
ϕ| = |θ − ϕ|
for any two points θ, ϕ ∈ T. This just says that the map R
α
is a rigid rotation that
does not change the distance between points. Let m = j − i. Hence
|R
m
α
0| = |x
j−i
− x
0
|
= |R
i
α
x
j−i
− R
i
α
x
0
| = |x
j
− x
i
| < ε.
It is also important that x
m
is not 0. This follows because α/2π is irrational.
So we observe that
R
km
α
0 ≡ kx
m
(mod 2π) for k ≥ 0
forms a sequence of points that move around the circle in steps smaller than ε. So
it is possible to choose k so that kx
m
is close to ϕ − θ, and thus
|ϕ − R
km
α
θ| = |(ϕ − θ) − R
km
α
0| = |(ϕ − θ) − kx
m
| < ε.
So every orbit is dense in the whole circle.
