Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®

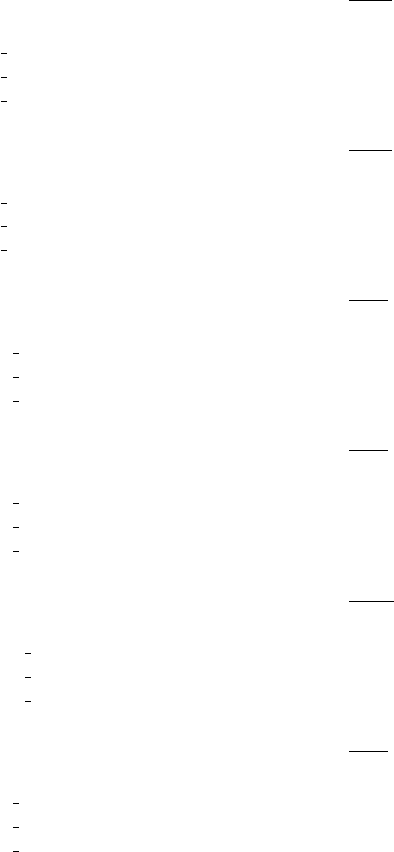
6.5 RRT Robot Arm 237

Q

1

= T

01x

,

Q

2

= T

12y

−gm

2

L

2

c

2

−gm

3

c

2

(L

2

+ q

3

),

Q

3

= F

23z

−gm

3

s

2

. (6.41)

The MATLAB statements for the partial velocity

∂

ω

10

∂ ˙q

r

, r = 1, 2, 3 are:

w1

1 = deriv(w10, diff(q1,t));

w1

2 = deriv(w10, diff(q2,t));

w1

3 = deriv(w10, diff(q3,t));

The MATLAB statements for the partial velocity

∂

ω

20

∂ ˙q

r

, r = 1, 2, 3 are:

w2

1 = deriv(w20, diff(q1,t));

w2

2 = deriv(w20, diff(q2,t));

w2

3 = deriv(w20, diff(q3,t));

The MATLAB statements for the partial velocity

∂ v

C

2

∂ ˙q

r

, r = 1, 2, 3 are:

vC1

1 = deriv(vC1, diff(q1,t));

vC1

2 = deriv(vC1, diff(q2,t));

vC1

3 = deriv(vC1, diff(q3,t));

The MATLAB statements for the partial velocity

∂ v

C

2

∂ ˙q

r

, r = 1, 2, 3 are:

vC2

1 = deriv(vC2, diff(q1,t));

vC2

2 = deriv(vC2, diff(q2,t));

vC2

3 = deriv(vC2, diff(q3,t));

The MATLAB statements for the partial velocity

∂ v

C

32

∂ ˙q

r

, r = 1, 2, 3 are:

vC32

1 = deriv(vC32, diff(q1,t));

vC32

2 = deriv(vC32, diff(q2,t));

vC32

3 = deriv(vC32, diff(q3,t));

The MATLAB statements for the partial velocity

∂ v

C

3

∂ ˙q

r

, r = 1, 2, 3 are:

vC3

1 = deriv(vC3, diff(q1,t));

vC3

2 = deriv(vC3, diff(q2,t));

vC3

3 = deriv(vC3, diff(q3,t));

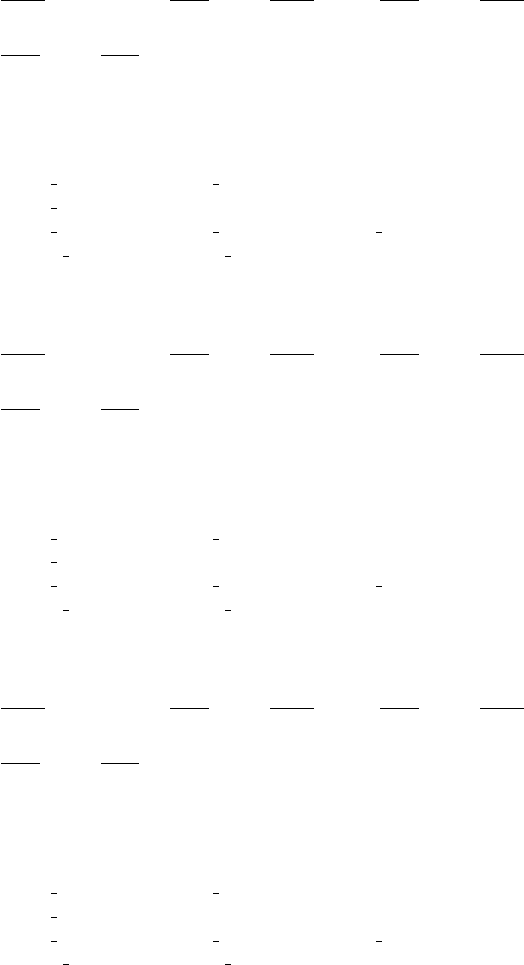
238 6 Analytical Dynamics of Open Kinematic Chains

The generalized active force Q

1

is

Q

1

=

∂

ω

10

∂ ˙q

1

·(T

01

−T

12

)+

∂ v

C

1

∂ ˙q

1

·G

1

+

∂

ω

20

∂ ˙q

1

·T

12

+

∂ v

C

2

∂ ˙q

1

·G

2

+

∂ v

C

32

∂ ˙q

1

·(−F

23

)

+

∂ v

C

3

∂ ˙q

1

·G

3

+

∂ v

C

3

∂ ˙q

1

·F

23

,

and the MATLAB statement for the generalized active force Q

1

is:

% generalized active force Q1

Q1=w1

1

*

T01.’ + vC1 1

*

G1.’ +...

w1

1

*

transpose(R21)

*

(-T12.’) +...

w2

1

*

T12.’ + vC2 1

*

G2.’ + vC32 1

*

(-F23.’) +...

vC3

1

*

F23.’ + vC3 1

*

G3.’

The generalized active force Q

2

is:

Q

2

=

∂

ω

10

∂ ˙q

2

·(T

01

−T

12

)+

∂ v

C

1

∂ ˙q

2

·G

1

+

∂

ω

20

∂ ˙q

2

·T

12

+

∂ v

C

2

∂ ˙q

2

·G

2

+

∂ v

C

32

∂ ˙q

2

·(−F

23

)

+

∂ v

C

3

∂ ˙q

2

·G

3

+

∂ v

C

3

∂ ˙q

2

·F

23

,

and the MATLAB statement for the generalized active force Q

2

is:

% generalized active force Q2

Q2=w1

2

*

T01.’ + vC1 2

*

G1.’ +...

w1

2

*

transpose(R21)

*

(-T12.’) +...

w2

2

*

T12.’ + vC2 2

*

G2.’ + vC32 2

*

(-F23.’) +...

vC3

2

*

F23.’ + vC3 2

*

G3.’

The generalized active force Q

3

is

Q

3

=

∂

ω

10

∂ ˙q

3

·(T

01

−T

12

)+

∂ v

C

1

∂ ˙q

3

·G

1

+

∂

ω

20

∂ ˙q

3

·T

12

+

∂ v

C

2

∂ ˙q

3

·G

2

+

∂ v

C

32

∂ ˙q

3

·(−F

23

)

+

∂ v

C

3

∂ ˙q

3

·G

3

+

∂ v

C

3

∂ ˙q

3

·F

23

,

and the MATLAB statement for the generalized active force Q

3

is

% generalized active force Q3

Q3=w1

3

*

T01.’ + vC1 3

*

G1.’ +...

w1

3

*

transpose(R21)

*

(-T12.’) +...

w2

3

*

T12.’ + vC2 3

*

G2.’ + vC32 3

*

(-F23.’) +...

vC3

3

*

F23.’ + vC3 3

*

G3.’

6.5 RRT Robot Arm 239

Kinetic Energy

The total kinetic energy of the robot arm in the reference frame (0) is

T =

3

∑

i=1

T

i

.

The kinetic energy of the link i, i = 1, 2,3, is

T

i

=

1

2

m

i

v

C

i

·v

C

i

+

1

2

ω

i0

·(

¯

I

i

·ω

i0

).

Remark: The kinetic energy for a rigid body is

T

rigidbody

=

1

2

mv

C

·v

C

+

1

2

ω ·(

¯

I

C

·ω),

where m is the mass of the rigid body, v

C

is the velocity of the mass center of the

rigid body in (0),

ω = ω

x

ı + ω

y

j + ω

z

k is the angular velocity of the rigid body in

(0), and

¯

I =(I

x

ı)ı+(I

y

j)j+(I

z

k)k is the central inertia dyadic of the rigid body. The

central principal axes of the rigid body are parallel to ı, j

, k and the associated mo-

ments of inertia have the values I

x

, I

y

, I

z

, respectively. The inertia matrix associated

with

¯

I is

¯

I →

⎡

⎣

I

x

00

0 I

y

0

00I

z

⎤

⎦

.

The dot product of the vector

ω with the dyadic

¯

I is

ω ·

¯

I =

¯

I ·ω = ω

x

I

x

ı + ω

y

I

y

j + ω

z

I

z

k.

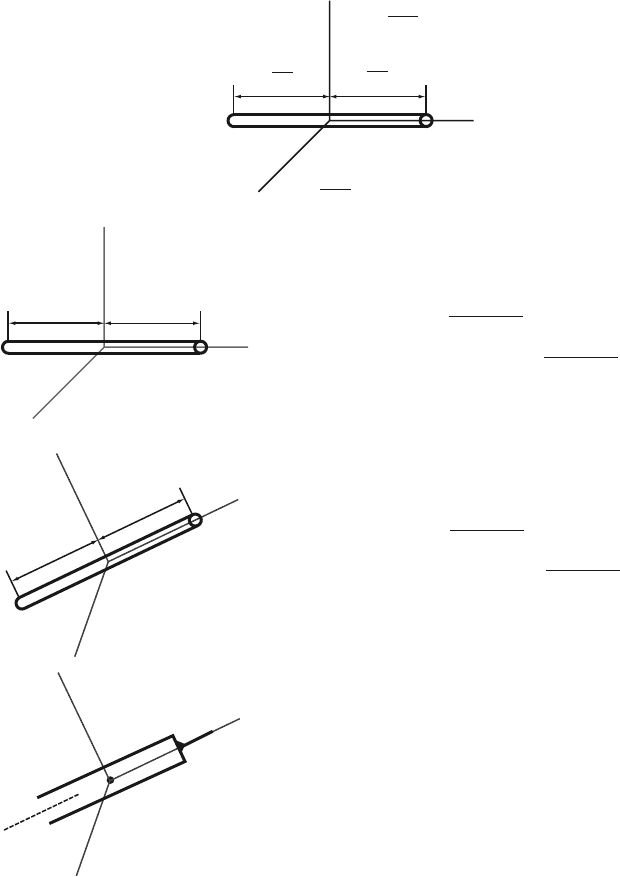
The central moments of inertia of links 1 and 2 are calculated using Fig. 6.6. The

central principal axes of 1 are parallel to ı

1

, j

1

, k

1

and the associated moments of

inertia have the values I

1x

, I

1y

, I

1z

, respectively. The inertia matrix associated with

link 1 is

¯

I

1

→

⎡

⎣

I

1x

00

0 I

1y

0

00I

1z

⎤

⎦

=

⎡

⎢

⎣

m

1

(2L

1

)

2

12

00

0

m

1

(2L

1

)

2

12

0

000

⎤

⎥

⎦

=

⎡

⎢

⎣

m

1

L

2

1

3

00

0

m

1

L

2

1

3

0

000

⎤

⎥

⎦

.

The central principal axes of 2 and 3 are parallel to ı

2

, j

2

, k

2

and the associated

moments of inertia have values I

2x

, I

2y

, I

2z

, and I

3x

, I

3y

, I

3z

respectively.

240 6 Analytical Dynamics of Open Kinematic Chains

I

1 x

I

1 y

I

1 z

¯

I

1

→

⎡

⎢

⎣

I

1x

00

0 I

1y

0

00I

1z

⎤

⎥

⎦

=

⎡

⎢

⎣

m

1

(2 L

1

)

2

12

00

0

m

1

(2 L

1

)

2

12

0

000

⎤

⎥

⎦

¯

I

2

→

⎡

⎢

⎣

I

2x

00

0 I

2y

0

00I

2z

⎤

⎥

⎦

=

⎡

⎢

⎣

m

2

(2 L

2

)

2

12

00

0

m

2

(2 L

2

)

2

12

0

000

⎤

⎥

⎦

¯

I

3

→

⎡

⎢

⎣

I

3 x

00

0 I

3 y

0

00 I

3 z

⎤

⎥

⎦

ml

2

12

=

I

x

ml

2

12

=

I

z

y

=

I

y

0

C

l

2

l

2

1

ı

k

1

j

1

A

C

1

B

L

1

L

1

2

ı

k

2

j

B

C

2

L

2

L

2

ı

k

2

j

C

3

Fig. 6.6 Central moments of inertia

6.5 RRT Robot Arm 241

The inertia matrix associated with link 2 is

¯

I

2

→

⎡

⎣

I

2x

00

0 I

2y

0

00I

2z

⎤

⎦

=

⎡

⎢

⎣

m

2

(2L

2

)

2

12

00

0

m

2

(2L

2

)

2

12

0

000

⎤

⎥

⎦

=

⎡

⎢

⎣

m

2

L

2

3

00

0

m

2

L

2

3

0

000

⎤

⎥

⎦

.

The inertia matrix associated with the slider 3 is

¯

I

3

→

⎡

⎣

I

3x

00

0 I

3y

0

00I

3z

⎤

⎦

.

The MATLAB commands for inertia matrices associated with the central inertia

dyadics are:

% inertia mat. associated with central inertia dyadic

% for link 1 expressed in terms of RF1 {i1,j1,k1}

I1 = [m1

*

(2

*

L1)ˆ2/12 0 0; 0 m1

*

(2

*

L1)ˆ2/12 0;000];

% inertia mat. associated with central inertia dyadic

% for link 2 expressed in terms of RF2 i2,j2,k2

I2 = [m2

*

(2

*

L2)ˆ2/12 0 0; 0 m2

*

(2

*

L2)ˆ2/12 0;000];

% inertia mat. associated with central inertia dyadic

% for link 3 expressed in terms of RF2 {i2,j2,k2}

syms I3x I3y I3z real

I3 = [I3x 0 0; 0 I3y 0; 0 0 I3z];

The kinetic energy of link 1 is

T

1

=

1

2

m

1

v

C

1

·v

C

1

+

1

2

ω

10

·(

¯

I

1

·ω

10

)=

1

2

m

1

L

1

˙q

2

1

+

1

6

m

1

L

1

˙q

2

1

=

2

3

m

1

L

1

˙q

2

1

.

The kinetic energy of bar 2 is

T

2

=

1

2

m

2

v

C

2

·v

C

2

+

1

2

ω

20

·(

¯

I

2

·ω

20

)

=

m

2

3



6L

2

1

+ L

2

+ 6L

1

L

2

c

2

+ L

2

cos2q

2



˙q

2

1

+ 2L

2

˙q

2



.

The kinetic energy of link 3 is

T

3

=

1

2

m

3

v

C

3

·v

C

3

+

1

2

ω

20

·(

¯

I

3

·ω

20

)

=

1

2

{I

3x

c

2

˙q

2

1

+ I

3z

s

2

˙q

2

1

+ I

3y

˙q

2

+m

3

!

(2L

1

+ L

2

c

2

+ c

2

q

3

)

2

˙q

2

1

+(L

2

+ q

3

)

2

˙q

2

+ ˙q

2

3

"

}.

242 6 Analytical Dynamics of Open Kinematic Chains

The total kinetic energy of the robot arm is

T = T

1

+ T

2

+ T

3

,

and is symbolically calculated in the program given in Appendix E.3. The MAT-

LAB commands for the total kinetic energy of the robot arm are:

T1 = (1/2)

*

m1

*

vC1

*

vC1.’ + (1/2)

*

w10

*

I1

*

w10.’

T2 = (1/2)

*

m2

*

vC2

*

vC2.’ + (1/2)

*

w20

*

I2

*

w20.’

T3 = (1/2)

*

m3

*

vC3

*

vC3.’ + (1/2)

*

w20

*

I3

*

w20.’

T = expand(T1 + T2 + T3); % total kinetic energy

Lagrange’s Equations of Motion

The left-hand sides of Lagrange’s equations are

d

dt



∂ T

∂ ˙q

r



−

∂ T

∂ q

r

, r = 1, 2, 3.

To arrive at the dynamical equations governing the robot arm, all that remains to be

done is to substitute into Lagrange’s equations, namely,

d

dt



∂ T

∂ ˙q

r



−

∂ T

∂ q

r

= Q

r

, r = 1, 2, 3.

The left-hand side of Lagrange’s equations are symbolically calculated in MATLAB

with:

% deriv(f, g(t)) differentiates f

% with respect to g(t)

Tdq1 = deriv(T, diff(q1,t));

Tdq2 = deriv(T, diff(q2,t));

Tdq3 = deriv(T, diff(q3,t));

Tt1 = diff(Tdq1, t);

Tt2 = diff(Tdq2, t);

Tt3 = diff(Tdq3, t);

Tq1 = deriv(T, q1);

Tq2 = deriv(T, q2);

Tq3 = deriv(T, q3);

LHS1 = Tt1 - Tq1;

LHS2 = Tt2 - Tq2;

LHS3 = Tt3 - Tq3;

6.5 RRT Robot Arm 243

Lagrange’s equations are symbolically calculated in MATLAB with:

Lagrange1 = LHS1-Q1;

Lagrange2 = LHS2-Q2;

Lagrange3 = LHS3-Q3;

The following feedback control laws are used

T

01x

= −β

01

˙q

1

−γ

01

(q

1

−q

1 f

),

T

12y

= −β

12

˙q

2

−γ

12

(q

2

−q

2 f

)+gm

2

L

2

c

2

+ gm

3

c

2

(L

2

+ q

3

),

F

23z

= −β

23

˙q

3

−γ

23

(q

3

−q

3 f

)+gm

3

s

2

. (6.42)

The constant gains are: β

01

= 450 N ms/rad, γ

01

= 300 N m/rad, β

12

= 200 N ms/rad,

γ

12

= 300 Nm/rad, β

23

= 150 Ns/m, and γ

23

= 50 N/m.

The MATLAB commands for the control torques are:

q1f=pi/3; q2f=pi/3; q3f=0.3;

b01=450; g01=300;

b12=200; g12=300;

b23=150; g23=50;

T01xc = -b01

*

diff(q1,t)-g01

*

(q1-q1f);

T12yc = -b12

*

diff(q2,t)-g12

*

(q2-q2f)+...

g

*

(m2

*

L2+m3

*

(L2+q3))

*

c2;

F23zc = -b23

*

diff(q3,t)-g23

*

(q3-q3f)+g

*

m3

*

s2;

tor = {T01x, T12y, F23z};

torf = {T01xc,T12yc,F23zc};

Lagrange’s equations with the feedback control laws are:

Lagrang1 = subs(Lagrange1, tor, torf);

Lagrang2 = subs(Lagrange2, tor, torf);

Lagrang3 = subs(Lagrange3, tor, torf);

Lagrange’s equations with the numerical values for input data are:

data = {L1, L2, I3x, I3y, I3z, m1, m2, m3, g};

datn = {0.4, 0.4, 5, 4, 1, 90, 60, 40, 9.81};

Lagran1 = subs(Lagrang1, data, datn);

Lagran2 = subs(Lagrang2, data, datn);

Lagran3 = subs(Lagrang3, data, datn);

The three second-order Lagrange’s equations have to be rewritten as a ﬁrst-order

system:

244 6 Analytical Dynamics of Open Kinematic Chains

ql = {diff(q1,t,2), diff(q2,t,2), diff(q3,t,2), ...

diff(q1,t), diff(q2,t), diff(q3,t), q1, q2, q3};

qf = {’ddq1’, ’ddq2’, ’ddq3’,...

’x(2)’, ’x(4)’, ’x(6)’, ’x(1)’, ’x(3)’, ’x(5)’};

%ql qf

%----------------------------

% diff(’q1(t)’,t,2) -> ’ddq1’

% diff(’q2(t)’,t,2) -> ’ddq2’

% diff(’q3(t)’,t,2) -> ’ddq3’

% diff(’q1(t)’,t) -> ’x(2)’

% diff(’q2(t)’,t) -> ’x(4)’

% diff(’q3(t)’,t) -> ’x(6)’

% ’q1(t)’ -> ’x(1)’

% ’q2(t)’ -> ’x(3)’

% ’q3(t)’ -> ’x(5)’

Lagra1 = subs(Lagran1, ql, qf);

Lagra2 = subs(Lagran2, ql, qf);

Lagra3 = subs(Lagran3, ql, qf);

% solve e.o.m. for ddq1, ddq2, ddq3

sol = solve(Lagra1,Lagra2,Lagra3,’ddq1,ddq2,ddq3’);

Lagr1 = sol.ddq1;

Lagr2 = sol.ddq2;

Lagr3 = sol.ddq3;

dx2dt = char(Lagr1);

dx4dt = char(Lagr2);

dx6dt = char(Lagr3);

The system of differential equations is solved numerically by m-ﬁle functions. The

function ﬁle, RRT

Lagr.m is created using the statements:

fid = fopen(’RRT

Lagr.m’,’w+’);

fprintf(fid,’function dx = RRT

Lagr(t,x)\n’);

fprintf(fid,’dx = zeros(6,1);\n’);

fprintf(fid,’dx(1) = x(2);\n’);

fprintf(fid,’dx(2) = ’);

fprintf(fid,dx2dt);

fprintf(fid,’;\n’);

fprintf(fid,’dx(3) = x(4);\n’);

fprintf(fid,’dx(4) = ’);

fprintf(fid,dx4dt);

fprintf(fid,’;\n’);

6.5 RRT Robot Arm 245

fprintf(fid,’dx(5) = x(6);\n’);

fprintf(fid,’dx(6) = ’);

fprintf(fid,dx6dt);

fprintf(fid,’;’);

fclose(fid);

cd(pwd);

The ode45 solver is used for the system of differential equations:

t0=0;

tf = 15;

time = [0 tf];

x0 = [pi/18 0 pi/6 0 0.25 0];

[t,xs] = ode45(@RRT

Lagr, time, x0);

x1 = xs(:,1);

x2 = xs(:,2);

x3 = xs(:,3);

x4 = xs(:,4);

x5 = xs(:,5);

x6 = xs(:,6);

subplot(3,1,1),...

plot(t,x1

*

180/pi,’r’),...

xlabel(’t (s)’),ylabel(’q1 (deg)’),grid,...

subplot(3,1,2),...

plot(t,x3

*

180/pi,’b’),...

xlabel(’t (s)’),ylabel(’q2 (deg)’),grid,...

subplot(3,1,3),...

plot(t,x5,’g’),...

xlabel(’t (s)’),ylabel(’q3 (m)’),grid

[ts,xs] = ode45(@RRT

Lagr,0:1:5,x0);

fprintf(’Results \n\n’)

fprintf...

(’t(s) q1(rad) q2(rad) q3(m) \n’)

[ts,xs(:,1),xs(:,3),xs(:,5)]

Figure 6.7 shows the plots of q

1

(t), q

2

(t), q

3

(t) and a MATLAB computer program

for the direct dynamics is given in Appendix E.3.

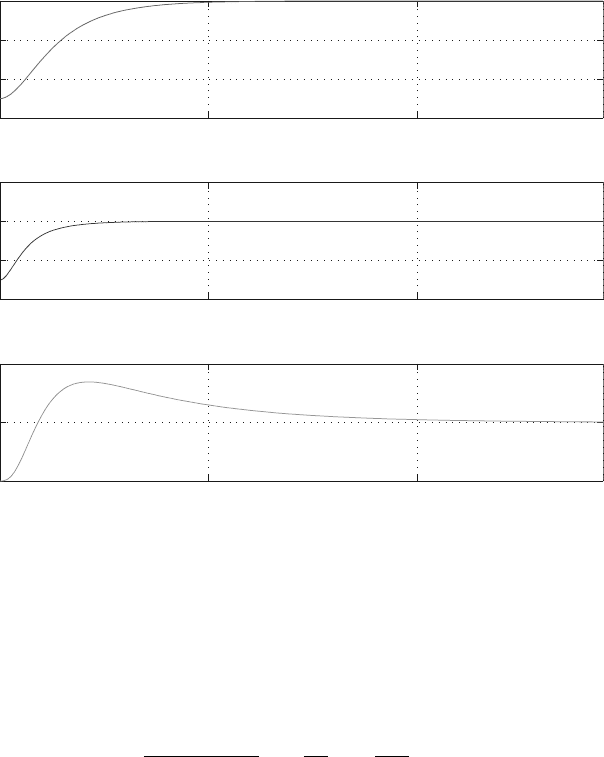
246 6 Analytical Dynamics of Open Kinematic Chains

0 5 10

0

20

40

60

t (s)

q1 (deg)

0 5 10

20

40

60

80

t (s)

q2 (deg)

0 5 10

0.25

0.3

0.35

t (s)

q3 (m)

Fig. 6.7 Solution plots for the generalized coordinates q

1

(t), q

2

(t), and q

3

(t)

6.5.2 Inverse Dynamics

A desired motion of the robot arm is speciﬁed for a time interval 0 ≤t ≤ T

p

= 15 s.

The generalized coordinates can be established explicitly

q

r

(t)=q

r

(0)+

q

r

(T

p

) −q

r

(0)

T

p



t −

T

p

2π

sin



2π t

T

p



, r = 1, 2,3, (6.43)

with q

r

(T

p

)=q

rf

.

The initial conditions, at t = 0s,areq

1

(0)=π/18 rad, q

2

(0)=π/6 rad, q

3

(0)=

0.25 m, and ˙q

1

(0)= ˙q

2

(0)= ˙q

3

(0)=0. The robot arm can be brought from an

initial state of rest in reference frame (0) to a ﬁnal state of rest in (0) in such a way

that q

1

, q

2

, and q

3

have speciﬁed values q

1

(T

p

)=q

1 f

= π/3 rad, q

2

(T

p

)=q

2 f

=

π/3 rad, and q

3

(T

p

)=q

3 f

= 0.3 m. Figure 6.8 shows the plots of q

1

(t), q

2

(t), and

q

3

(t) rad.

The MATLAB commands for ﬁnding the Lagrage’s equations are identical with

the previous commands presented in Sect. 6.5.1:

Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®

Подождите немного. Документ загружается.