Dan B. Marghitu, Mechanisms and Robots Analysis with MATLAB®
Подождите немного. Документ загружается.

6.4 Rotation Transformation 227
transposes the following relation is obtained
[
ı
j
k
]
⎡
⎣
p
x
p
y
p
z
⎤
⎦
=[
ı
j
k
][R
]
T
⎡
⎣
p
x
p
y
p
z
⎤
⎦
.
With [R
]
T
= R the above equation leads to
⎡
⎣
p
x
p
y
p
z
⎤
⎦
= R
⎡
⎣
p
x
p
y
p
z
⎤
⎦
.
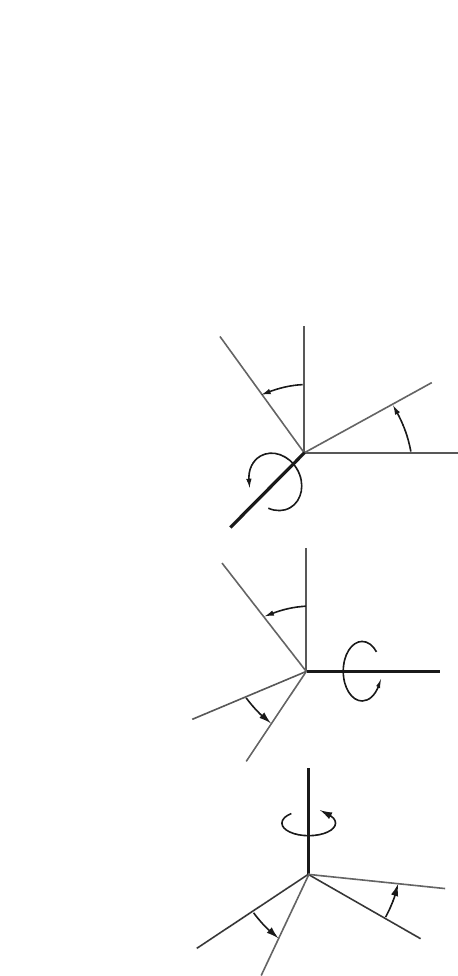
When the reference frame x
y
z
is the result of a simple rotation about one of the
axes of the reference frame xyz the following transformation matrices are obtained
(Fig. 6.4):
Fig. 6.4 x
y
z
as a result of a
simple rotation about one of
the axes of xyz
y
y
z
x
y
y
z
z
θ
x
θ
x
θ
x
y
z
x
θ
y
θ
y
θ
y
θ
z
θ
z
θ
z
x
x
z
x
x
y

228 6 Analytical Dynamics of Open Kinematic Chains
• the reference frame xyz is rotated by an angle θ
x
about the x-axis
R(x,θ
x
)=R(θ
x
)=
⎡
⎣
10 0
0 cos θ
x
sinθ
x
0 −sin θ
x
cosθ
x
⎤
⎦
,
• the reference frame xyz is rotated by an angle θ
y
about the y-axis
R(y,θ
y
)=R(θ
y
)=
⎡
⎣
cosθ
y
0 −sin θ
y
01 0
sinθ
y
0 cos θ
y
⎤
⎦
,
• the reference frame xyz is rotated by an angle θ
y
about the z-axis
R(z,θ
z
)=R(θ
z
)=
⎡
⎣
cosθ
z
sinθ
z
0
−sin θ
z
cosθ
z
0
001
⎤
⎦
.
The following property holds
R(s,−θ
s
)=R
T
(s,θ
s
), s = x, y, z.
6.5 RRT Robot Arm
Figure 6.5 is a schematic representation of a RRT robot arm consisting of three
links 1, 2, and 3. Let m
1
, m
2
, m
3
be the masses of 1, 2, 3, respectively. Link 1 can
be rotated at A in a “fixed” reference frame (0) of unit vectors [ı
0
, j
0
, k
0
] about a
vertical axis ı
0
. The unit vector ı
0
is fixed in 1. The link 1 is connected to link 2 at
the pin joint B. The element 2 rotates relative to 1 about an axis fixed in both 1 and 2,
passing through B, and perpendicular to the axis of 1. The last link 3 is connected to
2 by means of a slider joint. The mass centers of links 1, 2, and 3 are C
1
, C
2
, and C
3
,
respectively. The distances L
1
= AC
1
, L
B
= AB = 2 L
1
, and L
2
= BC
2
are indicated
in Fig. 6.5a The length of link 1 is 2L
1
and the length of link 2 is 2L
2
. The reference
frame (1) of the unit vectors [ı
1
, j
1
, k
1
] is attached to link 1, and the reference frame
(2) of the unit vectors [ı
2
, j
2
, k
2
] is attached to link 2, as shown in Fig. 6.5b.
6.5.1 Direct Dynamics
Generalized Coordinates and Transformation Matrices
The generalized coordinates (quantities associated with the the instantaneous posi-
tion of the system) are q
1
(t), q
2
(t), q
3
(t). The first generalized coordinate q
1
denotes
the radian measure of the angle between the axes of (1) and (0).
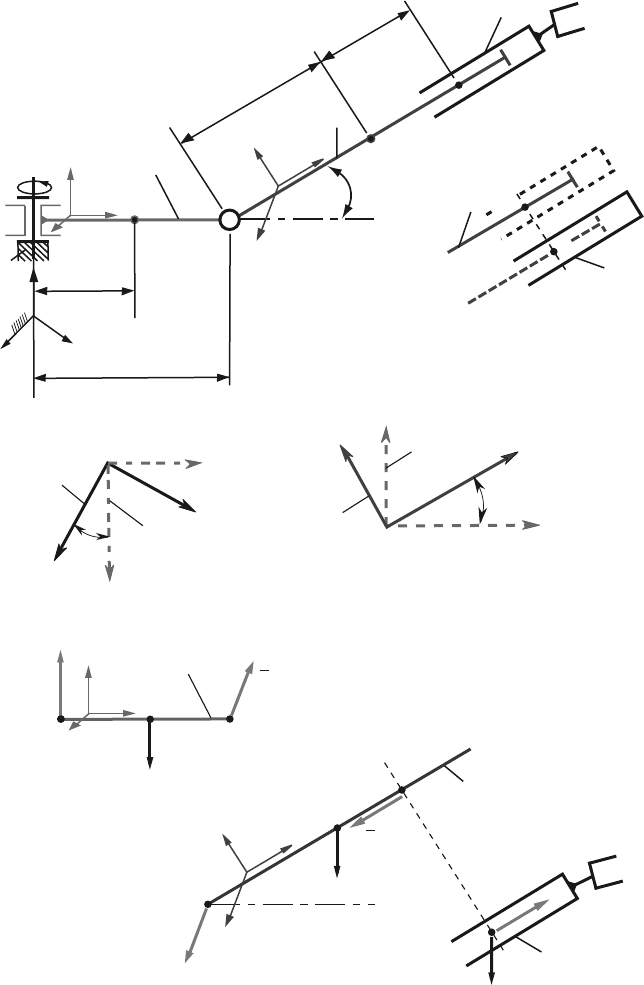
6.5 RRT Robot Arm 229
(b)
k
1
k
2
1
ı
2
ı
(1)
(2)
q
2
(a)
2
L
B
=
C
32
0
k
0
j
1
k
1
j
q
1
(0)
(1)
2
B
A
1
1
k
ı
j
1
1
T
01 x
CC
1
G
1
1
ı
T
12 y
2
j
k
0
0
j
1
ı
0
ı
A
B
L
1
q
1
q
2
q
3
L
1
L
2
k
1
1
j
0
C
1
1
k
2
2
ı
2
j
2
2
3
3
C
2
C
3
C
3
B
T
12y
CC
2
G
2
2
j
C
32
G
3
F
23z
2
k
F
23z
2
k
(c)
3
k
2
2
ı
2
j
C
3
Fig. 6.5 RRT robot arm

230 6 Analytical Dynamics of Open Kinematic Chains
The unit vectors ı
1
, j
1
, and k
1
can be expressed as functions of ı
0
, j
0
, and k
0
ı
1
= ı
0
,
j
1
= c
1
j
0
+ s
1
k
0
,
k
1
= −s
1
j
0
+ c
1
k
0
, (6.26)
or
⎡
⎣
ı
1
j
1
k
1
⎤
⎦
=
⎡
⎣
10 0
0 c
1
s
1
0 −s
1
c
1
⎤
⎦
⎡
⎣
ı
0
j
0
k
0
⎤
⎦
,
where s
1
= sinq
1
and c
1
= cosq
1
. The transformation matrix from (1) to (0) is
R
10
=
⎡
⎣
10 0
0 c
1
s
1
0 −s
1
c
1
⎤
⎦
. (6.27)
The second generalized coordinate also designates a radian measure of the rotation
angle between (1) and (2). The unit vectors ı
2
, j
2
and k
2
can be expressed as
ı
2
= c
2
ı
1
−s
2
k
1
= c
2
ı
0
+ s
1
s
2
j
0
−c
1
s
2
k
0
,
j
2
= j
1
,
= c
1
j
0
+ s
1
k
0
,
k
2
= s
2
ı
1
+ c
2
k
1
= s
2
ı
0
−c
2
s
1
j
0
+ c
1
c
2
k
0
, (6.28)
where s
2
= sinq
2
and c
2
= cosq
2
. The transformation matrix from (2) to (1) is
R
21
=
⎡
⎣
c
2
0 −s
2
01 0
s
2
0 c
2
⎤
⎦
. (6.29)
The last generalized coordinate q
3
is the distance from C
2
to C
3
. The MATLAB
commands for the transformation matrices are:
q1 = sym(’q1(t)’);
q2 = sym(’q2(t)’);
q3 = sym(’q3(t)’);
c1 = cos(q1);
s1 = sin(q1);
c2 = cos(q2);
s2 = sin(q2);
6.5 RRT Robot Arm 231
% transformation matrix from RF1 to RF0
R10 = [[1 0 0]; [0 c1 s1]; [0 -s1 c1]];
% transformation matrix from RF2 to RF1
R21 = [[c2 0 -s2]; [0 1 0]; [s2 0 c2]];
Angular Velocities
Next, the angular velocity of the links 1, 2, and 3 will be expressed in the fixed
reference frame (0). The angular velocity of 1 in (0) is
ω
10
= ˙q
1
ı
1
. (6.30)
The angular velocity of the link 2 with respect to (1) is
ω
21
= ˙q
2
j
2
.
The angular velocity of the link 2 with respect to the fixed reference frame (0) is
ω
20
= ω
10
+ ω
21
= ˙q
1
ı
1
+ ˙q
2
j
2
.
With ı
0
= ı
1
= c
2
ı
2
+ s
2
k
2
the angular velocity of the link 2 in the reference frame
(0) written in terms of the reference frame (2) is
ω
20
= ˙q
1
(c
2
ı
2
+ s
2
k
2
)+ ˙q
2
j
2
= ˙q
1
c
2
ı
2
+ ˙q
2
j
2
+ ˙q
1
s
2
k
2
. (6.31)
The link 3 has the same rotational motion as link 2, i.e.,
ω
30
= ω
20
.
Angular Accelerations
The angular acceleration of the link 1 in the reference frame (0) is
α
10
= ¨q
1
ı
1
. (6.32)
The angular acceleration of the link 2 with respect to the reference frame (0) is
α
20
=
d
dt
ω
20
=
(2)
d
dt
ω
20
+ ω
20
×ω
20
=
(2)
d
dt
ω
20
,
where
(2)
d
dt
represents the derivative with respect to time in reference frame (2),
[ı
2
,j
2
,k
2
]. The angular acceleration of the link 2 is
α
20
=
(2)
d
dt
( ˙q
1
c
2
ı
2
+ ˙q
2
j
2
+ ˙q
1
s
2
k
2
)
=(¨q
1
c
2
− ˙q
1
˙q
2
s
2
)ı
2
+ ¨q
2
j
2
+(¨q
1
s
2
+ ˙q
1
˙q
2
c
2
)k
2
. (6.33)
The link 3 has the same angular acceleration as link 2, i.e.,
α
30
= α
20
.

232 6 Analytical Dynamics of Open Kinematic Chains
The MATLAB commands for the angular velocities and accelerations are:
% angular velocity of link 1 in RF0
% expressed in terms of RF1 {i1,j1,k1}
w10 = [diff(q1,t)00];
% angular velocity of link 2 in RF0
% expressed in terms of RF1 {i1,j1,k1}
w201 = [diff(q1,t) diff(q2,t) 0];
% angular velocity of link 2 in RF0
% expressed in terms of RF2 {i2,j2,k2}
w20 = w201
*
transpose(R21);
% angular acceleration of link 1
% in RF0 expressed in terms of RF1 {i1,j1,k1}
alpha10 = diff(w10,t);
% angular acceleration of link 2 in RF0
% expressed in terms of RF2 {i2,j2,k2}
alpha20 = diff(w20,t);
Linear Velocities
The position vector of C
1
, the mass center of link 1, is
r
C
1
= L
1
k
1
,
and the velocity of C
1
in (0) is
v
C
1
=
d
dt
r
C
1
=
(1)
d
dt
r
C
1
+ ω
10
×r
C
1
= 0 +
ı
1
j
1
k
1
˙q
1
00
00L
1
= −˙q
1
L
1
j
1
. (6.34)
With MATLAB the position and velocity vectors of C
1
are:
% position vector of mass center C1 of link 1
% in RF0 expressed in terms of RF1 {i1,j1,k1}
rC1 = [0 0 L1];
% linear velocity of mass center C1 of link 1
% in RF0 expressed in terms of RF1 {i1,j1,k1}
vC1 = diff(rC1,t) + cross(w10, rC1);

6.5 RRT Robot Arm 233
The position vector of C
2
, the mass center of link 2, is
r
C
2
= L
B
k
1
+ L
2
k
2
= L
B
(−s
2
ı
2
+ c
2
k
2
)+L
2
k
2
= −L
B
s
2
ı
2
+(L
B
c
2
+ L
2
)k
2
,
where L
B
= 2L
1
. The velocity of C
2
in (0) is
v
C
2
=
d
dt
r
C
2
=
(2)
d
dt
r
C
2
+ ω
20
×r
C
2
= −L
B
c
1
˙q
2
ı
2
−L
B
c
2
˙q
2
k
2
+
ı
2
j
2
k
2
˙q
1
c
2
˙q
2
˙q
1
s
2
−L
B
s
2
0 L
B
c
2
+ L
2
= L
2
˙q
2
ı
2
−(L
B
+ L
2
c
2
) ˙q
1
j
2
. (6.35)
The position and velocity vectors of C
2
, with MATLAB, are:
% position vector of mass center C2 of link 2
% in RF0 expressed in terms of RF2 {i2,j2,k2}
rC2=[002
*
L1]
*
transpose(R21) + [0 0 L2];
% linear velocity of mass center C2 of link 2
% in RF0 expressed in terms of RF2 {i2,j2,k2}
vC2 = simple(diff(rC2,t) + cross(w20,rC2));
The position vector of C
3
with respect to reference frame (0) is
r
C
3
= r
C
2
+ q
3
k
2
= −L
B
s
2
ı
2
+(L
B
c
2
+ L
2
+ q
3
)k
2
,
and the velocity of this mass center in (0) is
v
C
3
=
d
dt
r
C
3
=
(2)
d
dt
r
C
3
+ ω
20
×r
C
3
= −L
B
c
2
˙q
2
ı
2
−(L
B
c
2
˙q
2
+ ˙q
3
)k
2
+
ı
2
j
2
k
2
˙q
1
c
2
˙q
2
˙q
1
s
2
−L
B
s
2
0 L
B
c
2
+ L
2
+ q
3
=(L
2
+ q
3
) ˙q
2
ı
2
−(L
B
+ L
2
c
2
+ c
2
q
2
) ˙q
1
j
2
+ ˙q
3
k
2
. (6.36)
The position and velocity vectors of C
3
, with MATLAB, are:
% position vector of mass center C3 of link 3 in RF0
% expressed in terms of RF2 {i2,j2,k2}
rC3 = rC2 + [0 0 q3];

234 6 Analytical Dynamics of Open Kinematic Chains
% linear velocity of mass center C3 of link 3 in RF0
% expressed in terms of RF2 {i2,j2,k2}
vC3 = simple(diff(rC3,t) + cross(w20,rC3));
There is a point C
32
on link 2 (C
32
∈ link 2) that instantaneously coincides with C
3
,
(C
3
∈ link 3). The velocity of point C
32
is
v
C
32
= v
C
2
+ ω
20
×r
C
2
C
3
= v
C
2
+ ω
20
×q
3
k
2
=(L
2
+ q
3
) ˙q
2
ı
2
−(L
B
+ L
2
c
2
+ c
2
q
2
) ˙q
1
j
2
. (6.37)
The point C
32
of link 2 is superposed with the point C
3
of link 3. The velocity of
mass center C
3
of link 3 in (0) can be computed in terms of the velocity of C
32
using
the relation
v
C
3
= v
C
32
+ ˙q
3
k
2
.
The velocity vector of C
32
, with MATLAB, is:
vC32 = simple(vC2 + cross(w20,[0 0 q3]));
Linear Accelerations
The acceleration of C
1
is
a
C
1
=
d
dt
v
C
1
=
(1)
d
dt
v
C
1
+ ω
10
×v
C
1
= −L
1
¨q
1
j +
ı
1
j
1
k
1
˙q
1
00
0 −L
1
˙q
1
0
= −L
1
¨q
1
j
1
−L
1
˙q
2
1
k
1
. (6.38)
The linear acceleration of the mass center C
2
is
a
C
2
=
d
dt
v
C
2
=
(2)
d
dt
v
C
2
+ ω
20
×v
C
2
. (6.39)
The linear acceleration of C
2
is symbolically calculated in the program given in
Appendix E.3. The acceleration of C
3
is
a
C
3
=
d
dt
v
C
3
=
(2)
d
dt
v
C
3
+ ω
20
×v
C
3
. (6.40)
The linear acceleration of C
1
, C
2
, and C
3
are symbolically calculated with MAT-
LAB:
aC1 = simple(diff(vC1,t)+cross(w10,vC1));
aC2 = simple(diff(vC2,t)+cross(w20,vC2));
aC3 = simple(diff(vC3,t)+cross(w20,vC3));

6.5 RRT Robot Arm 235
Generalized Forces
Remark: If a set of contact and/or body forces acting on a rigid body is equivalent
to a couple of torque T together with force R applied at a point P of the rigid body,
then the contribution of this set of forces to the generalized force, Q
r
,isgivenby
Q
r
=
∂
ω
∂ ˙q
r
·T +
∂ v
P
∂ ˙q
r
·R, r = 1, 2,...,
where
ω is the angular velocity of the rigid body in (0), v
P
is the velocity of P in
(0), and r represents the generalized coordinates.
In the case of the robotic arm, there are two kinds of forces that contribute to the
generalized forces Q
1
, Q
2
, and Q
3
namely, contact forces applied in order to drive
the links 1, 2, and 3, and gravitational forces exerted on 1, 2, and 3 by the Earth. The
set of contact forces transmitted from 0 to 1 can be replaced with a couple of torque
T
01
applied to 1 at A, Fig. 6.5c. Similarly, the set of contact forces transmitted from
1 to 2 can be replaced with a couple of torque T
12
applied to 2 at B, Fig. 6.5c. The
law of action and reaction then guarantees that the set of contact forces transmitted
from 1 to 2 is equivalent to a couple of torque −T
12
to1atB. Next, the set of contact
forces exerted by link 2 on link 3 can be replaced with a force F
23
applied to 3 at
C
3
, Fig. 6.5c. The law of action and reaction guarantees that the set of contact forces
transmitted from 3 to 2 is equivalent to a force −F
23
applied to 2 at C
32
. The point
C
32
(C
32
∈link 2) instantaneously coincides with C
3
,(C
3
∈link 3). The expressions
T
01
, T
12
, and F
23
are
T
01
= T
01x
ı
1
+ T
01y
j
1
+ T
01z
k
1
, T
12
= T
12x
ı
2
+ T
12y
j
2
+ T
12z
k
2
, and
F
23
= F
23x
ı
2
+ F
23y
j
2
+ F
23z
k
2
.
The MATLAB statements for the contact torques and contact force are:
syms T01x T01y T01z T12x T12y T12z F23x F23y F23z
% contact torque of 0 that acts on link 1
% in RF0 expressed in terms of RF1 {i1,j1,k1}
T01 = [T01x T01y T01z];
% contact torque of link 1 that acts on link 2
% in RF0 expressed in terms of RF2 {i2,j2,k2}
T12 = [T12x T12y T12z];
% contact force of link 2 that acts on link 3 at C3
% in RF0 expressed in terms of RF2 {i2,j2,k2}
F23 = [F23x F23y F23z];
The external gravitational forces exerted on the links 1, 2, and 3 by the Earth, can
be denoted by G
1
, G
2
, and G
3
respectively, Fig. 6.5c, and can be expressed as
G
1
= −m
1
gı
1
, G
2
= −m
2
gı
1
= −m
2
g(c
2
ı
2
+ s
2
k
2
), and
G
3
= −m
3
gı
1
= −m
3
g(c
2
ı
2
+ s
2
k
2
).

236 6 Analytical Dynamics of Open Kinematic Chains
The reason for replacing ı
1
with c
2
ı
2
+ s
2
k
2
in connection with the forces G
2
and
G
3
is that they are soon to be dot-multiplied with
∂ v
C
2
∂ ˙q
r
and
∂ v
C
3
∂ ˙q
r
That have been
expressed in terms of ı
2
,j
2
, and k
2
.
The MATLAB statements for the gravitational forces are:
% gravitational force that acts on link 1 at C1
% RF0 expressed in terms of RF1 {i1,j1,k1}
G1 = [-m1
*
g00]
% gravitational force that acts on link 2 at C2
% in RF0 expressed in terms of RF2 {i2,j2,k2}
G2 = [-m2
*
g00]
*
transpose(R21)
% gravitational force that acts on link 3 at C3
% in RF0 expressed in terms of RF2 {i2,j2,k2}
G3 = [-m3
*
g00]
*
transpose(R21)
One can express (Q
r
)
1
, the contribution to the generalized active force Q
r
of all the
forces and torques acting on the particles of the link 1, as
(Q
r
)
1
=
∂
ω
10
∂ ˙q
r
·(T
01
−T
12
)+
∂ v
C
1
∂ ˙q
r
·G
1
, r = 1, 2,3.
The contribution (Q
r
)
2
to the generalized active force of all the forces and torques
acting on the link 2 is
(Q
r
)
2
=
∂
ω
20
∂ ˙q
r
·T
12
+
∂ v
C
2
∂ ˙q
r
·G
2
+
∂ v
C
32
∂ ˙q
r
·(−F
23
), r = 1,2,3,
where v
C
32
= v
C
3
− ˙q
3
k
2
.
The contribution (Q
r
)
3
, to the generalized active force of all the forces and
torques acting on the link 3 is
(Q
r
)
3
=
∂ v
C
3
∂ ˙q
r
·G
3
+
∂ v
C
3
∂ ˙q
r
·F
23
, r = 1, 2,3.
The generalized active force Q
r
of all the forces and torques acting on the links 1,
2, and 3 are
Q
r
=(Q
r
)
1
+(Q
r
)
2
+(Q
r
)
3
=
∂
ω
10
∂ ˙q
r
·(T
01
−T
12
)+
∂ v
C
1
∂ ˙q
r
·G
1
+
∂
ω
20
∂ ˙q
r
·T
12
+
∂ v
C
2
∂ ˙q
r
·G
2
+
∂ v
C
32
∂ ˙q
r
·(−F
23
)
+
∂ v
C
3
∂ ˙q
r
·G
3
+
∂ v
C
3
∂ ˙q
r
·F
23
, r = 1, 2, 3.
The generalized forces Q
r
, r = 1,2,3 are symbolically calculated in the program
given in Appendix E.3 and have the values
