Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

IMMISCIBLE DISPLACEMENT 401

∂

∂∂

and since M = 1, the pressure gradients in the oil and water must be the same.

Therefore, if a constant pressure difference ∆p is applied between injection and

production wells, then

xxL

∂

∂∆

∂∂

in all layers, where L is the length of the reservoir block. Applying the Buckley Leverett

theory to calculate the velocity of the water in the j

layer, equ. (10.19)

jj w

wh S

æö

∆

ç÷

∆

èø

(10.75)

where w is the reservoir width and, at the front, for piston-like displacement,

worwc

S(1SS)

æö

∆

ç÷

∆−−

èø

Finally, since

jrw

qwh

′

∂

=−

∂

then equ. (10.75) can be expressed as

jrw

jw or wc

(1 S S ) L

φµ

′

∆

−−

One additional imposition, inherent in the assumption that M = 1 in all layers, is that the

ratio of end point relative permeabilities,

rw ro

k/k

′′

, is constant. The layer order in which

water will break through to the producing well will therefore be in the sequence of

decreasing values of

jrw

jorwc

(1 S S )

′

−−

(10.76)

Application of the Stiles method to generate averaged relative permeability curves

requires, as a preliminary, the re-ordering of the layer numbers in the sequence in

which water breakthrough will occur. Thus the sand having the highest value of ∝,

equ. (10.76), becomes layer number one; the sand having the second largest value of

a becomes layer number two, etc.

If there is a total of N layers in the reservoir then, observing the water breakthrough at

the producing well, the average saturation,

S , after breakthrough in the n

layer, can

be calculated using an equation which is identical in form to equ. (10.72). Similarly, the

IMMISCIBLE DISPLACEMENT 402

averaged relative permeabilities,

k and

k , can be calculated using equs. (10.73)

and (10.74), respectively. The averaged relative permeabilities so generated are, in

fact, independent of the position in the linear reservoir at which the flood is observed

and are not restricted to application at the wellbore. This is because, although there is

a difference in water velocity between any two sands, the difference remains constant

as the flood advances; this being implicit in the assumption of piston-like displacement.

When plotting the relative permeability curves, the separate points are not joined by

line segments but, instead, by step functions since after breakthrough in layer n the

relative permeabilities remain constant until breakthrough occurs in layer n+1 when

there is a discrete jump to the new values of

and

. If there are a large

number of separate layers in the reservoir the step functions can be smoothed into

continuous curves.

The main assumption in using the Stiles method, that M=1, should theoretically limit its

application to reservoirs in which this condition is approximately satisfied.

Nevertheless, it is frequently used as a starting point even when M > 1 and the

resulting relative permeability curves adjusted so that calculated oil recovery matches

that observed in pilot floods.

10.9 DISPLACEMENT WHEN THERE IS A TOTAL LACK OF VERTICAL EQUILIBRIUM

The generation of averaged relative permeability curves, described in secs. 10.6-8,

relies on the assumption that the oil displacement occurs under the vertical equilibrium

condition (refer sec. 10.2). Because of this it is possible to define both saturation and

relative permeability distributions with respect to thickness and averaging these

facilitates the description of two dimensional displacement using simple, one

dimensional equations.

A similar procedure can also be adopted for precisely the opposite flow condition, that

is, when there is an extreme lack of vertical equilibrium. This will occur when the fluid

velocity parallel to the bedding-greatly exceeds the velocity in the dipnormal direction.

In extreme cases the fluid saturations will be uniformly distributed with respect to

thickness, in a homogeneous reservoir, and the displacement can be described using

the rock relative permeability curves with the one dimensional Buckley-Leverett theory.

The corresponding pseudo capillary pressure relationship for such displacement is

simply

) =

−

= 0

In a stratified reservoir, a total lack of vertical equilibrium implies that the fluids will

move through each layer in isolation from fluids in adjacent layers. Since there is

negligible fluid movement in the dip-normal direction such displacement can be

described in one dimension using the method of Stiles for generating averaged relative

permeabilities

The methods described in this chapter for reducing the description of oil displacement

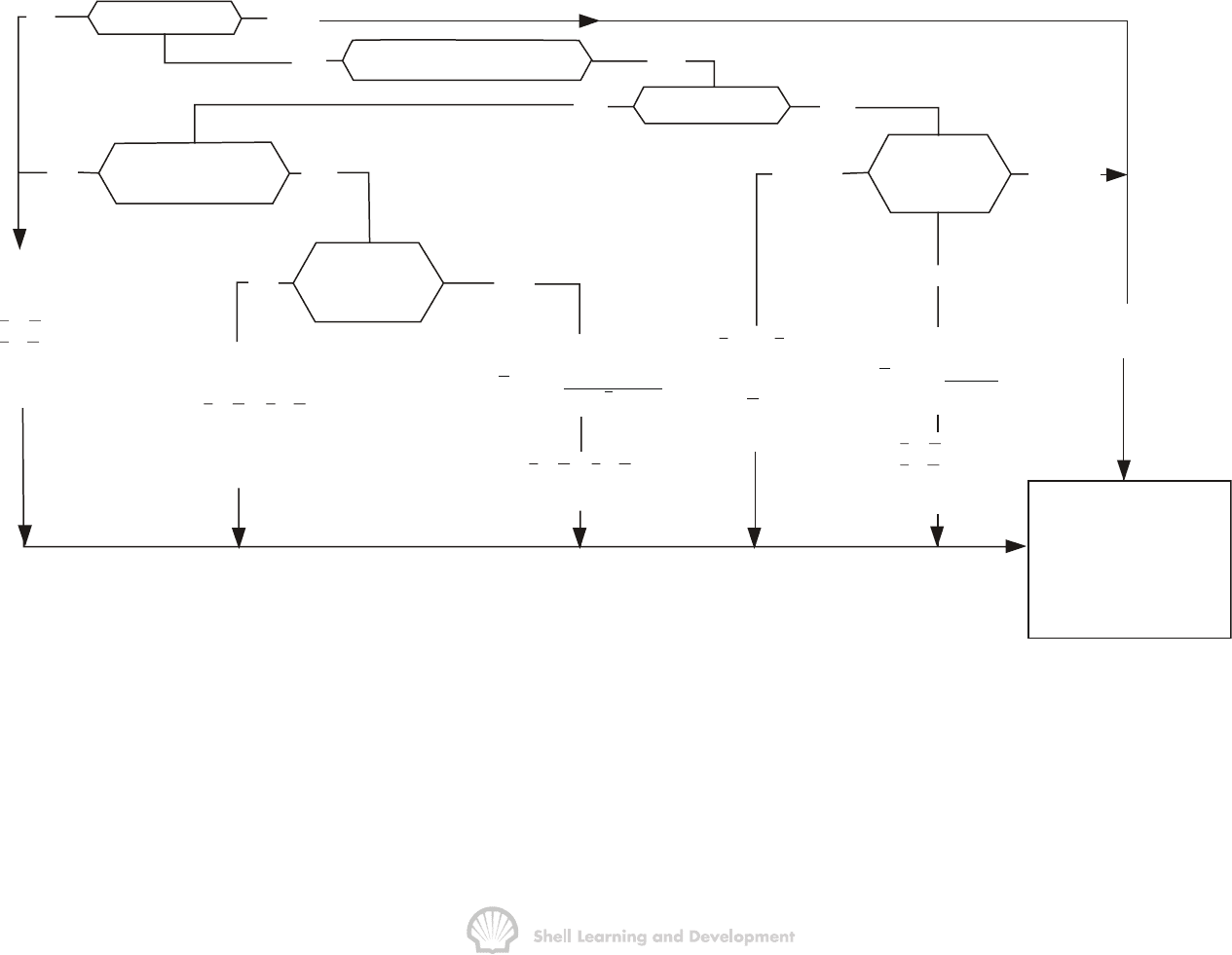
to one dimension are summarised in fig. 10.43. The starting point in this flow chart is

IMMISCIBLE DISPLACEMENT 403

the decision concerning the validity of the assumption of vertical equilibrium. To

attempt to describe oil displacement using ,simple analytical methods requires either

the assumption that vertical equilibrium predominates, or alternatively, that it does not

exist at all. In both cases averaged relative permeability curves can be generated for

use with the Buckley-Leverett, one dimensional, displacement theory.

Alternatively, the averaged relative permeability functions are used as basic input for

the numerical simulation of the displacement process. The following section will

describe the importance of using averaged relative permeabilities and pseudo capillary

pressures in numerical simulation. In addition, the manner in which the assumption of

vertical equilibrium can be verified, using numerical simulation, and the manner in

which displacement can be described under conditions intermediate between total and

non-existent vertical equilibrium, will also be described.

IMMISCIBLE DISPLACEMENT 404

Homogeneous

Yes

VERTICAL EQUILIBRIUM

Yes

Homogeneous

Yes

Capillary

Transition

Zone

H << h H >> h

Yes

Pressure

Communication

Yes

Capillary

Transition

Zone

Stiles

Method

rw w

()

as step functions

(sec. 10.8)

ro w

()

Direct cal-

culation of

as straight line

segments

(sec. 10.8; ex. 10.4)

kSkS

rw w ro w

( ), ( )

(sec. 10.8)

kSkS

rw w ro w

( ), ( )

ro rw

and

are linear

functions of

(sec. 10.6)

(sec. 10.7)

rw w

ro w

()

Rock relative

permeabilties

Buckly-Leverett

(application Welge

sec. 10.5; ex. 10.2)

Input Numerical

Simulation (sec. 10.10)

H h

(z)S (z)dz

S(z)dz

Fig. 10.43 Methods of generating averaged relative permeabilities, as functions of the thickness averaged water saturation, dependent on

the homogeneity of the reservoir and the magnitude of capillary transition zone (H). The chart is only applicable when the vertical

equilibrium condition pertains or when there is a total lack of vertical equilibrium

IMMISCIBLE DISPLACEMENT 405

10.10 THE NUMERICAL SIMULATION OF IMMISCIBLE, INCOMPRESSIBLE

DISPLACEMENT

So far, this text has concentrated on developing simple mathematical models to

describe the physics of reservoir depletion and fluid flow. Examples of these are the

zero dimensional material balance equation (Chapter 3) and the analytical solutions of

linear second order differential equations for radial flow (Chapters 5-8).

Sometimes, however, these simple models are totally inadequate to provide the

required solutions to reservoir engineering problems. In a strong natural water drive

reservoir, for instance, the zero dimensional material balance can be used to predict

the volume of water influx, but it can never predict where the water will preferentially

move in the reservoir and such knowledge may be required to determine the location of

additional production or injection wells. Furthermore, not all reservoir problems can be

formulated in terms of linear differential equations for which standard solutions can be

sought. Nobody, for instance, would attempt to solve simultaneously the equations for

three phase (oil — water—gas) flow in three dimensions with irregular boundary

conditions, using an analytical approach. To deal with complex reservoir problems the

engineer must resort to numerical simulation methods and particularly so for

displacement problems, in which one of the main aims is to determine the areal

distribution of fluids in the reservoir resulting from a flood.

A numerical simulator is a computer program which permits the user to divide the

reservoir into discrete grid blocks which may each be characterised by having different

reservoir properties. The flow of fluids from block to block is governed by the principle

of mass conservation coupled with Darcy's law. Flow into or out of a block, due to

presence of an injection or production well, is also catered for. Most simulators are

capable of solving large sets of second order differential equations for the

simultaneous flow of oil, gas and water, in three dimensions. In addition the effects of

natural water influx, fluid compressibility, mass transfer between gas and liquid phases

and the variation of such parameters as porosity and permeability, as functions of

pressure, can all be modelled. The differential equations themselves are generally

formulated using the finite difference analogue for first and second order differentials

and solved simultaneously using numerical techniques with some acceptable, small

error attached to each solution.

It is not intended, in this text, to describe numerical simulation in any great detail.

Indeed, at the time of writing, such a description would require not merely another text

book but a small encyclopaedia. Instead, since this chapter has concentrated on the

generation of averaged relative permeabilities and pseudo capillary pressures, as

functions of the thickness averaged water saturation; the description of simulation will

be confined to the way in which these vitally important parameters are handled by the

simulator. To accomplish this, the simple case of linear, incompressible displacement

of oil by water will be considered, for which the appropriate mass conservation

equations for reservoir fluids will be presented. This simplifies and concentrates the

description since the pressure dependent terms, densities and viscosities, can safely

be regarded as being independent of pressure. Thus only the variation in time and

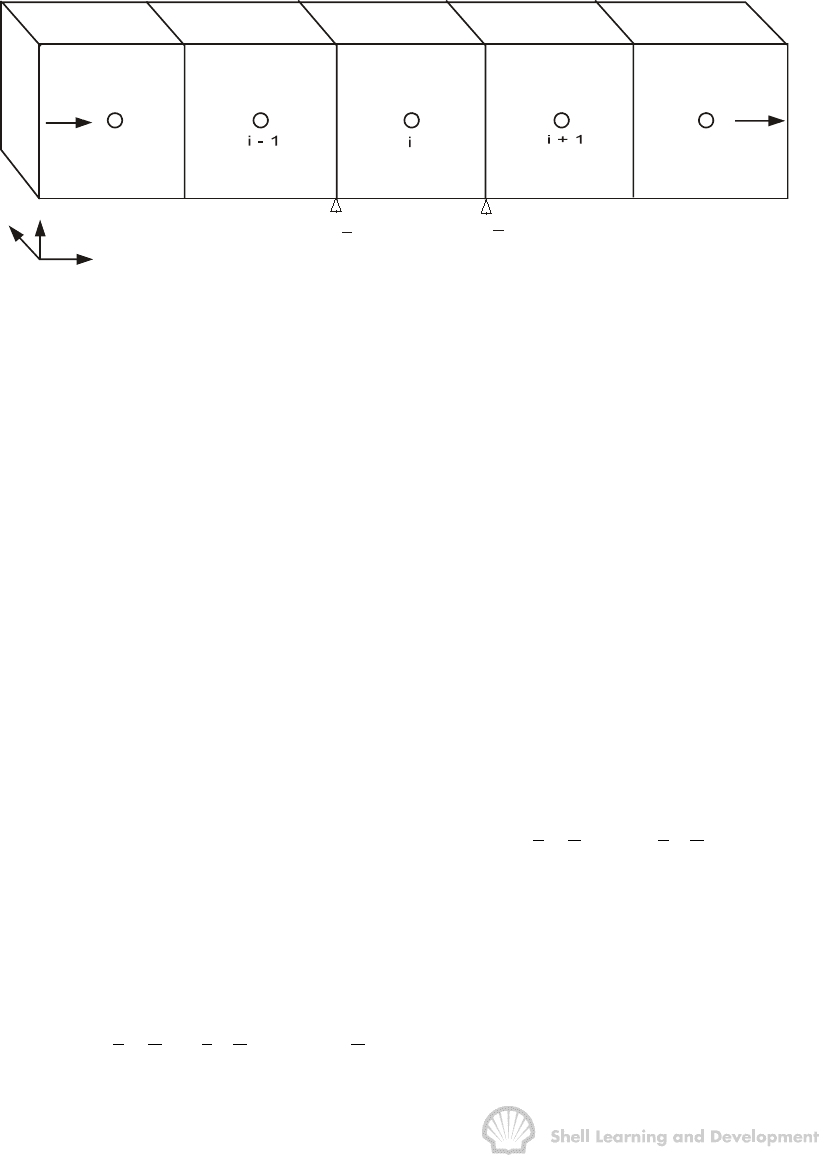
IMMISCIBLE DISPLACEMENT 406

space of the water saturation and saturation dependent functions is considered, but

this description is equally applicable to more complex simulations.

For those unfamiliar with numerical simulation methods, references 18-20, at the end

of this chapter, provide a more general introduction to the subject, while the selected

AIME papers

give details of the more successful mathematical techniques employed,

together with a selection of field case histories which have been interpreted using

numerical simulation methods.

Consider the displacement of oil by water in the linear, horizontal, homogeneous

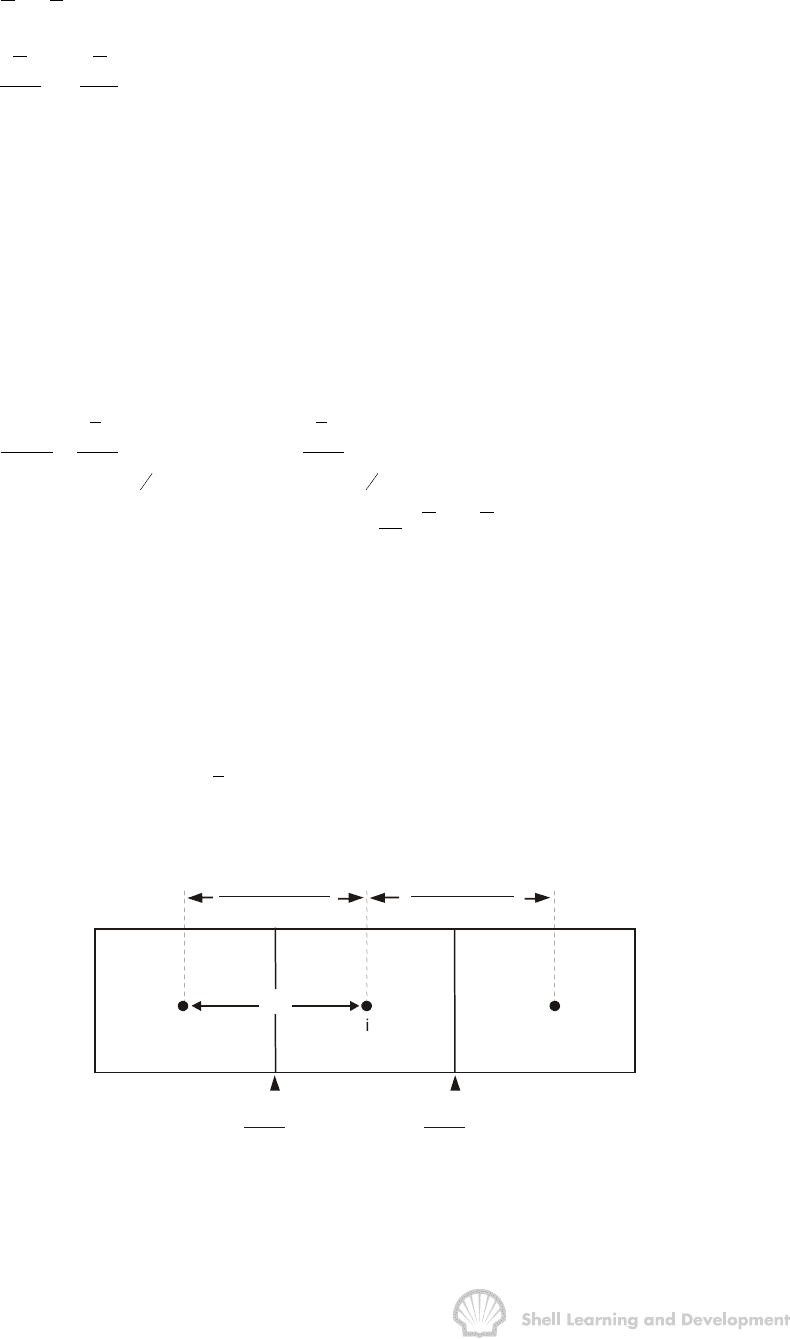
reservoir element shown in fig.10.44.

−

Fig. 10.44 Numerical simulation model for linear displacement in a homogeneous

reservoir

For simulation purposes the element has been subdivided into a row of discrete,

regular grid blocks. The geometrical centre of each grid block is called a node and

these points are numbered in increasing sequence from left to right. At first glance it

may appear that this simple model is three dimensional since the geometry is defined

by regular Cartesian coordinates. What the reservoir simulator deals with internally,

however, are sets of grid block averaged data concentrated at each node and, since

these are discrete points in space, this has the effect of reducing the flow description to

one dimension.

At any time the data used by the simulator, for each node, consists of the average oil

and water pressures in each block together with the corresponding pressure

dependent functions, the fluid densities and viscosities. In the case of incompressible

displacement, these can be considered as constants. Also used are the average water

saturation and the saturation dependent relative permeabilities and capillary pressures.

Since no allowance is made for the variation of any parameter across the width of a

grid block (y-direction), the average saturations used are the thickness averaged

values,S

, and the relative permeabilities are the values

k(S) and

k(S), the

generation of which, for a homogeneous reservoir, has been described in detail in

sec. 10.7. Finally, the saturation dependent capillary pressure used is the pseudo

capillary pressure or phase pressure difference at the centre of the grid block, which is

a function ofS

It is therefore necessary, even for such a simple, one dimensional problem, to provide

as basic input

k(S),

k(S)and

(S ), as functions ofS

(e.g. table 10.10),

IMMISCIBLE DISPLACEMENT 407

rather than the rock relative permeability and capillary pressure functions measured on

thin core plugs in the laboratory.

For this, or any other problem, the basic physical principle employed by the simulator is

that of mass conservation. Usually fluid quantities are conserved at stock tank

conditions and related to reservoir fluid quantities through the pressure dependent PVT

parameters. When studying the immiscible displacement of oil by water, however,

there- is no loss in generality in applying mass conservation directly to both fluids in the

reservoir.

Considering the one dimensional flow of water through a small volume element of

thickness dx, which may also contain a fluid source or sink (injection or production

well), the mass conservation of water can be expressed as

xdx

ww ww w ww

q q Adx ( S) Q

ρρ φρ ρ

∂

′

−= +

∂

(10.77)

This has the same form as equ. (10.13), which was used as the starting point of the

derivation of the Buckley-Leverett equation, except that now a mass source term

′

has been added; where

′

is the reservoir rate of water injection or production, for

which it conventionally has a positive or negative sign, respectively. Reducing the

equation to the form

ww w

(q ) A ( S )

xtdx

ρφρ

′

∂∂

−= +

∂∂

and substituting for the reservoir flow rate q

using Darcy's equation for horizontal flow

pkk A

∂

=−

∂

gives

pkk S

xx t

æö

∂∂∂

ç÷

∂∂ ∂

èø

(10.78)

in which it has been assumed that, for this incompressible displacement both

and

are constant, and Q

Q/Adx

′

which is the injection or production rate per unit of

reservoir bulk volume. Furthermore, in this, and in subsequent equations, the pressure

should be interpreted as the average value at the centre of the reservoir and the

viscosity evaluated at this same pressure.

The analogous equation to equ. (10.78) for the mass conservation of oil is

kk S

xx t

æö

∂

∂∂

ç÷

∂∂ ∂

èø

(10.79)

Instead of attempting to analytically solve either equ. (10.78) or (10.79), which was the

approach employed in developing the Buckley-Leverett displacement theory, the

IMMISCIBLE DISPLACEMENT 408

equations are expressed in finite difference form in the simulator and solved for the oil

and water pressures and saturations, using the ancillary equations

= p

−p

(pseudo capillary pressure) (10.80)

SS1+= (10.81)

and

∂∂

(10.82)

In expressing equs. (10.78) and (10.79) in finite difference form, the simulator

considers time and space to be discrete rather than continuous as for analytical

solutions. The time intervals, or time steps, are denoted by ∆t and, for this one

dimensional problem, the space increments by ∆x. For grid blocks of equal length,

∆x is the length of a block, which is also the distance between successive nodes.

Equation (10.78) is commonly formulated in finite difference terms using the so-called

central difference approximation for the left hand side which, for flow through grid block

i during the timestep ∆t, gives

rw rw

n1 n1 n1 n1

w,i 1 w,i w,i w,i 1

n1 n

1kk kk

(p p ) (p p )

(x)

(S S )

µµ

++ ++

+−

éù

æö æö

êú

−− −

ç÷ ç÷

êú∆

èø èø

ëû

=−

∆

(10.83)

in which it has been assumed, for the moment, that the grid block does not contain a

well.

The superscript n is attached to parameters evaluated at time t

and n+1 to parameters

evaluated at time t

n+1

, where t

n+1

− t

= ∆t, the current time step. Similarly the subscripts

i, i+½ and i-½ refer to parameters specified at the grid block nodes and grid block

faces, fig. (10.44). Flow between grid block i − 1 and i and between i and i+1 is

governed by the values of

kk /

evaluated at the grid block faces i − ½ and i+½ ,

respectively. The manner of the spatial linkage of the left hand side of equ. (10.83) can

be appreciated from fig.10.45.

∆

w,i

−

w,i−1

)

∆

i−½

k k

æö

ç÷

èø

i - 1 i + 1

w,i+1

−

w,i

)

∆

i+½

k k

æö

ç÷

èø

Fig. 10.45 Spatial linkage of the finite difference formulation of the left hand side of

equ (10.83).

IMMISCIBLE DISPLACEMENT 409

Similarly, equ. (10.79), for oil, can be expressed in finite difference terms as

ro ro

n1 n1 n1 n1

o,i 1 o,i o,i o,i 1

n1 n

o,i o,i

1kk kk

(p p ) (p p )

(x)

(S S )

µµ

++ ++

+−

éù

æö æö

êú

−− −

ç÷ ç÷

êú∆

èø èø

ëû

=−

∆

(10.84)

and adding equs. (10.83) and (10.84), using equ. (10.82) to eliminate the sum of the

time derivatives of the saturations, and equ. (10.80) expressed as

n1 n

,n 1 n 1 n 1 ,n n n

cowcow

P(S)p p P(S)pp

°+ + + °

=−≈ =− (10.85)

to substitute for p

n+1

, gives

rw ro ro

n 1 n 1 ,n ,n

o,i w,i c,i 1 c,i

wo o

rw ro ro

n1 n1

w,i w,i 1 c,i 1

wo o

1kkkk kk

(p p ) ( P P )

(x)

kk kk kk

(p p ) (P ) 0

µµ µ

−−

°°

æö æö

+−− −

ç÷ ç÷

ê∆

èø èø

æö æö

−+ −− =

ç÷ ç÷

èø èø

(10.86)

in which it is assumed, equ. (10.85), that while oil and water pressures may individually

change during a time step, the corresponding change in the pseudo capillary pressure

can be neglected.

The finite difference expression of equ. (10.86) is not unique, but is the one which has

been most commonly applied in reservoir simulation. In the equation the water

pressures are all dated at the new time level n+1, at which they are unknown, whereas

the k

term, which is both saturation and pressure dependent, and the pseudo

capillary pressures, equ. (10.85), which are saturation dependent, are all dated at the

old time level n at which their values are known. Therefore, equ. (10.86), which was

specifically formulated for the flow of water through grid block i, contains only three

unknowns

n1 n1 n1

w,i 1 w,i w,i 1

p,p andp

++ +

−+

but, when the equation is linked with the similar

equations for all the grid blocks in the one dimensional model (i = 1........n), the set of

equations can be solved simultaneously to determine the value of

in each block.

This simultaneous solution for pressures at the new time level is referred to as being

IMPLICIT in pressure.

Having obtained the values of

, for each grid block, the remainder of the solution at

time level n+1, and in the j

grid block, proceeds as follows:

− substitute the calculated values of

n1 n1 n1

w,i 1 w,i w,i 1

p,p andp

++ +

−+

in equ. (10.83) and solve

for

w,i

. (This is referred to as an EXPLICIT solution for

w,i

, since it is the only

unknown in the equation).

− the value of

w,i

is used to calculate

o,i

, since

w,i

o,i

= 1, equ. (10.81)

IMMISCIBLE DISPLACEMENT 410

− the value of

w,i

is used to determine

,n 1

c,i

+°

w,i

(S )

since the relationship between

pseudo capillary pressure and average water saturation is part of the input data

− the updated value of the pseudo capillary pressure is used to calculate

o,i

since

o,i

,n 1

c,i

+°

w,i

, equ. (10.85).

− and finally, the values of all the pressure and saturation dependent variables

(densities, viscosities, and relative permeabilities) are all updated at time level

n+1 using the newly determined pressures and saturations and the input tables

of these variables, as functions of pressure and saturation.

The procedure described above for the simulation of immiscible, incompressible

displacement of oil by water is one that can be readily extended to three phase flow.

The finite difference conservation equations for oil, gas and water, including the

possibility of mass transfer between the gas and liquid phases, are again summed to

eliminate the total time change in saturation during the time step

ttt

∂

++=

∂∂∂

This results in a more complex form of the water pressure equation, (10.86), in which

the oil and gas phase pressures can be eliminated using the pseudo capillary pressure

functions

n1 n n

coil o w

(P ) p p

+°

≈−

and

n1 n n

cgas g o

(P ) p p

+°

≈−

Thereafter, water pressures are solved for implicitly, and the remainder of the solution

proceeds in very much the same way as described above.

The method, in which pressures are determined

IMPLICITLY and saturations EXPLCITLY,

is known as the

IMPES solution technique. One of the main disadvantages in its

application is that in solving the water pressure equation, (10.86), at time level n+1, the

saturation dependent relative permeabilities and pseudo capillary pressures are

evaluated for the known water saturation at time level n. For problems in which the

water saturation change in a grid block can be large during a time step, such as when

sharp saturation fronts move through the reservoir, the evaluation o saturation

dependent functions at the old time level can lead to severe instabilities in the

IMPES

solution.