Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

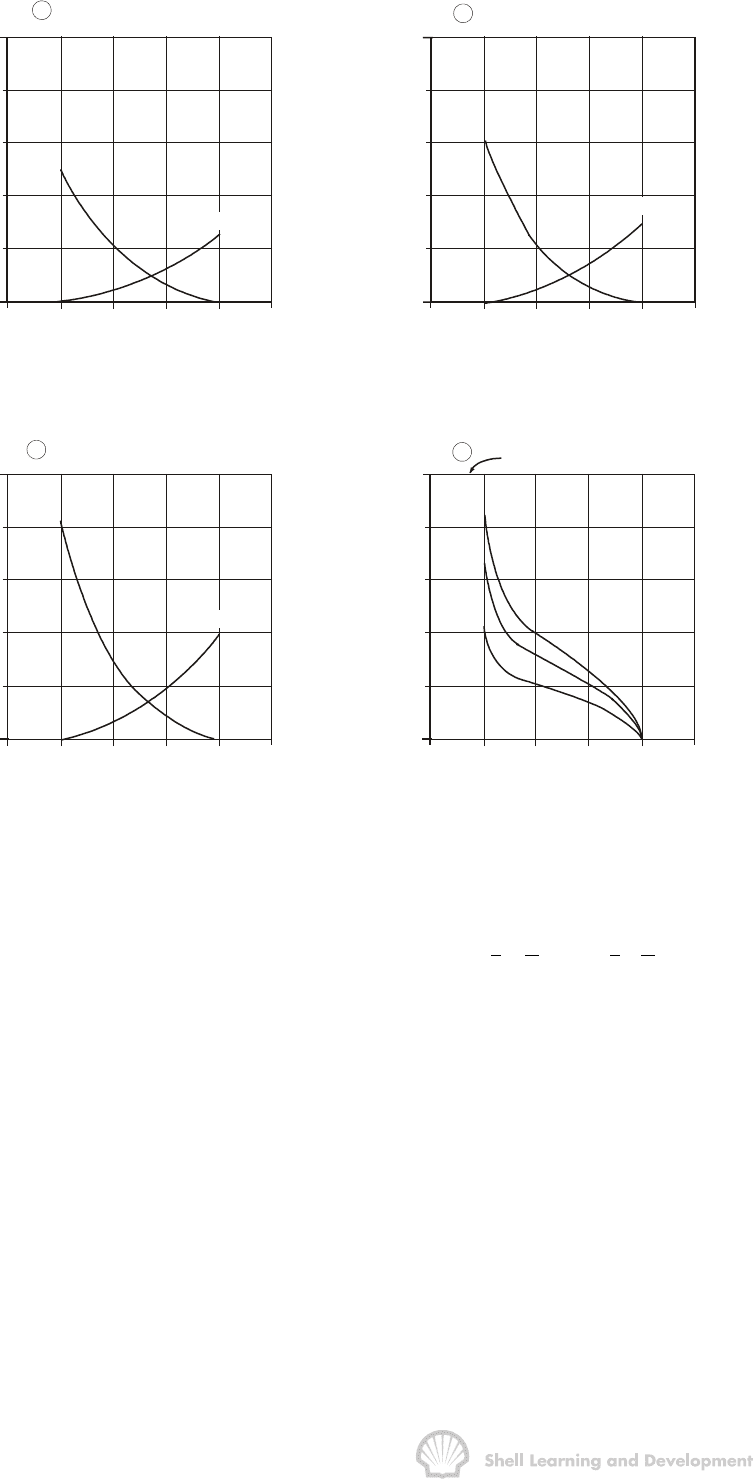
IMMISCIBLE DISPLACEMENT 391

1.0

.2 .4

.6 .8 1.0

OIL

WATER

LAYER 1

(psi)

0.2.4.6.81.0

(ft)

LAYER NUMBER

1.0

.2 .4

.6 .8 1.0

OIL

WATER

LAYER 3

1.0

.2 .4

.6 .8 1.0

OIL

WATER

LAYER 2

Fig. 10.35 (a)-(c) Rock relative permeabilities, and (d) laboratory measured capillary

pressures for the three layered reservoir shown in fig. 10.34

Averaged relative permeability curves can be generated by allowing the maximum

saturation, S

= 1 − S

, to rise in the reservoir and, assuming vertical equilibrium,

determining for each selected value of

−

values of S

k(S)and

k(S)as

described in the previous section. In the current example, as will be shown presently, it

is more convenient to use the pseudo capillary pressure as the independent variable,

since the pressures in the oil and water are continuous across the reservoir thickness,

whereas saturations are not. The values of P

will vary between + 2 psi, when

−

zero, and − 2 psi, when

−

= 40 ft, the latter corresponding to complete flood-out of

the reservoir at the point of observation. In total, five values of

have been selected

in the range between ± 2 psi for which the corresponding saturation and relative

permeability distributions have been plotted in figs.10.36 and 10.37.

IMMISCIBLE DISPLACEMENT 392

.2 .4

.6 .8 1.0

(ft)

= .396

.2 .4

.6 .8 1.

(ft)

= .042 ; k

= .510

P = 2 psi

Fig. 10.36 (a) Water saturation, and (b) relative permeability distributions, with respect

to thickness, when the saturation at the base of the layered reservoir

(fig. 10.34) is S

= 1−

−−

−S

° = 2 psi)

Consider the initial situation when

= 2 psi or

−

= 0. Table 10.11 lists the

corresponding phase pressure difference across the reservoir together with the water

saturation and relative permeability distributions which have been obtained from

fig. 10.35(a) - (d).

The oil and water pressures, and hence the phase pressure difference, are continuous

across the reservoir. The water saturation, however, is discontinuous at the layer

boundaries, fig. 10.36(a), since the saturation values in table 10.11 are obtained from

the three capillary pressure curves shown in fig. 10.35(d). Thus at the interface

between layers 1 and 2, where P

= 1.0 psi, the water saturation in layer 1 is 0.69 and

in layer 2 is 0.63. Similarly, since there are three sets of relative permeability curves

there are also discontinuities in the relative permeability distributions, to oil and water,

at the layer boundaries.

Layer z (ft) P

(psi) S

40 4.0 .2 0 .8

35 3.5 .2 0 .83

30 3.0 .2 0 .8

30 3.0 .22 .001 .55

25 2.5 .24 .003 .50

2.0

(P )

.29 .02 .40

15 1.5 .45 .07 .18

10 1.0 .63 .17 .05

10 1.0 .69 .18 .02

5 .5 .78 .23 .0021

0 0 .80 .24 0

TABLE 10.11

Phase pressure difference, water saturation and relative permeability distributions

for

= 2 psi; fig. 10.36

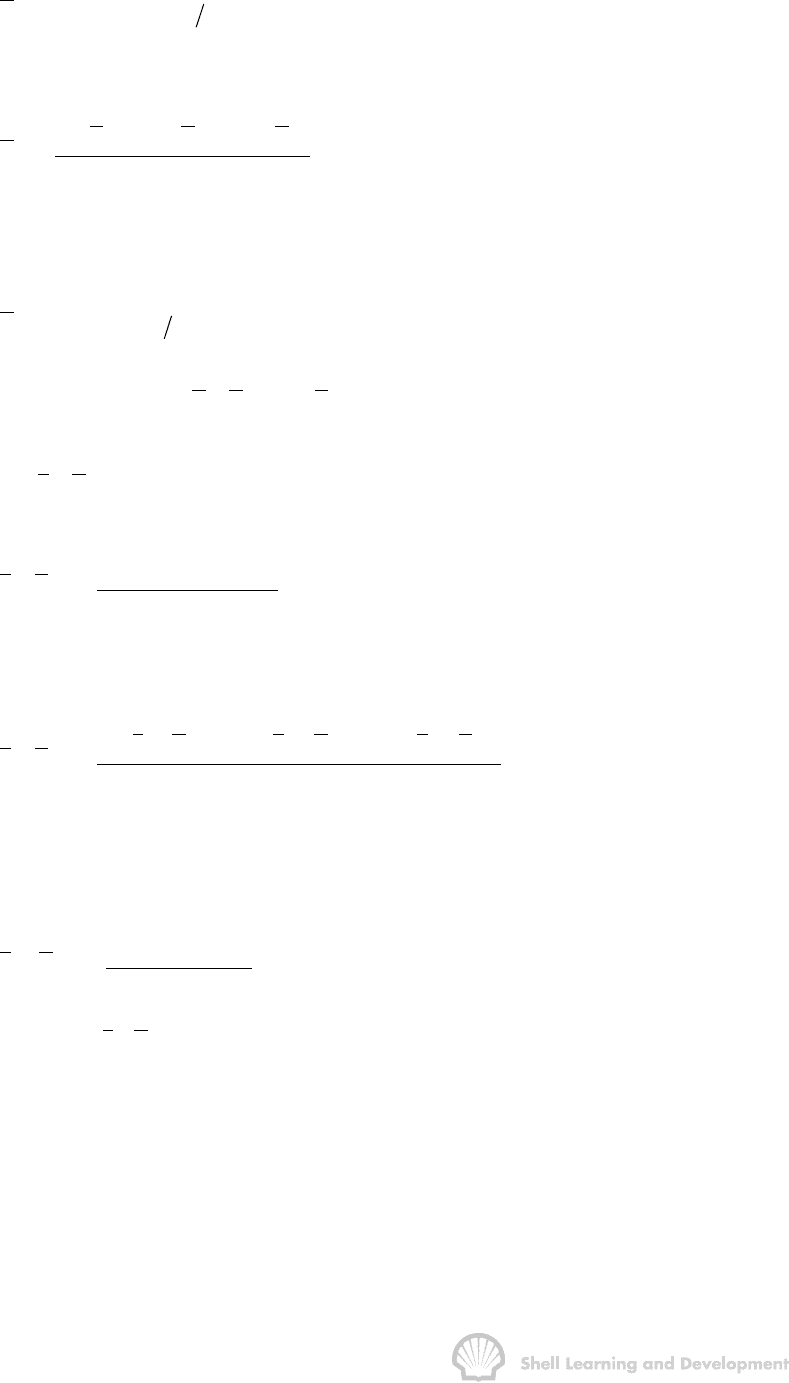
IMMISCIBLE DISPLACEMENT 393

For the saturation distribution depicted in fig.10.36(a) the average water saturation can

be evaluated mathematically as

S (z)S (z)dz (z)dz

φφ

òò

which, since there are three distinct, homogeneous layers, can be expressed as

12 3

ww w

11 22 33

hS hS hS

φφ φ

(10.71)

in which, for instance,

SS(z)dzh=

The average saturations,

12 3

ww w

S,S andS ,can be evaluated either graphically or

numerically, as described in the previous section.

Similarly,

k(S)can be evaluated as

rw w

k(z)k (S (z))dz

k(S)

k(z)dz

12 3

123

rw rw rw

ww w

11 2 2 3 3

hkk (S ) hk k (S ) hk k (S )

k(S)

where, for instance

rw w

k(S(z))dz

k(S)

and similarly for

k(S).

IMMISCIBLE DISPLACEMENT 394

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.0

.2 .4

.6 .8 1.

= .524

= .634

= .765

= .800

(ft)

= .100 ; k

= .395

rw ro

= .158 ; = .257

rw ro

= .338 ; = 0

rw ro

= .280 ; = .026

P = -2 psi

P = -1 psi

P = 0 psi

P = 1 psi

Fig. 10.37 (a)-(h) Water saturation and relative permeability distributions,as functions of

thickness,for various selected values of

(three layered reservoir, fig 10.34)

IMMISCIBLE DISPLACEMENT 395

Values of

S,k (S)and

k(S)are listed in table 10.12 and plotted in

figs. 10.39(a) and 10.38(a). The latter three have been obtained by the graphical

integration of the distributions shown in fig. 10.36(a) and (b) and fig. 10.37(a)-(h) for the

five selected values of

(psi)

S

k

7.0 .200 0 .678

2.0 .396 .042 .510

1.0 .524 .100 .395

0 .634 .158 .257

-1.0 .765 .280 .026

-2.0 .800 .338 0

TABLE 10.12

Pseudo capillary pressure and averaged relative permeabilities

corresponding to figs. 10.36 and 10.37

In particular, when S

= 0.2, the connate water saturation, then using the capillary

pressure curve for layer 1, fig. 10.35(d), the phase pressure at the base of the reservoir

must be at least 5 psi and hence

= 7 psi.

The method described above is perfectly general and can be applied equally well when

the end point saturations also vary from layer to layer. The case studied is for the

gradation of permeabilities from high to low from the top to the bottom of the reservoir.

If the reservoir shown in fig. 10.34 were inverted, repetition of the above exercise

would yield the averaged relative permeability and pseudo capillary pressure curves

shown in figs. 10.38(b) and 10.39(a) (dashed curve). The corresponding fractional flow

curves for the two cases are plotted in fig. 10.39(b) assuming that

= 5 cp and

= .5 cp, as in exercises 10.2 and 10.3. The latter curves indicate that the more

favourable displacement occurs when the high permeability layer is uppermost in the

reservoir. In this case the injected water will preferentially travel through the top layer

and in doing so will be pulled downwards, due to the gravity difference between the

water and oil, resulting in fairly even saturation distribution. If, however, the high

permeability layer is at the base of the reservoir, capillary forces will tend to suck up

the water but this is not as effective in creating a uniform saturation distribution.

A special, simple case of the method of averaging presented in this section occurs

when the capillary transition zone in each layer is negligible so that flow occurs under

segregated conditions, as described in sec. 10.6. Suppose there are a total of N layers

in the reservoir. When the water-oil interface has risen so that it coincides with the top

of the n

layer, the thickness averaged water saturation is, in analogy with equ. (10.71)

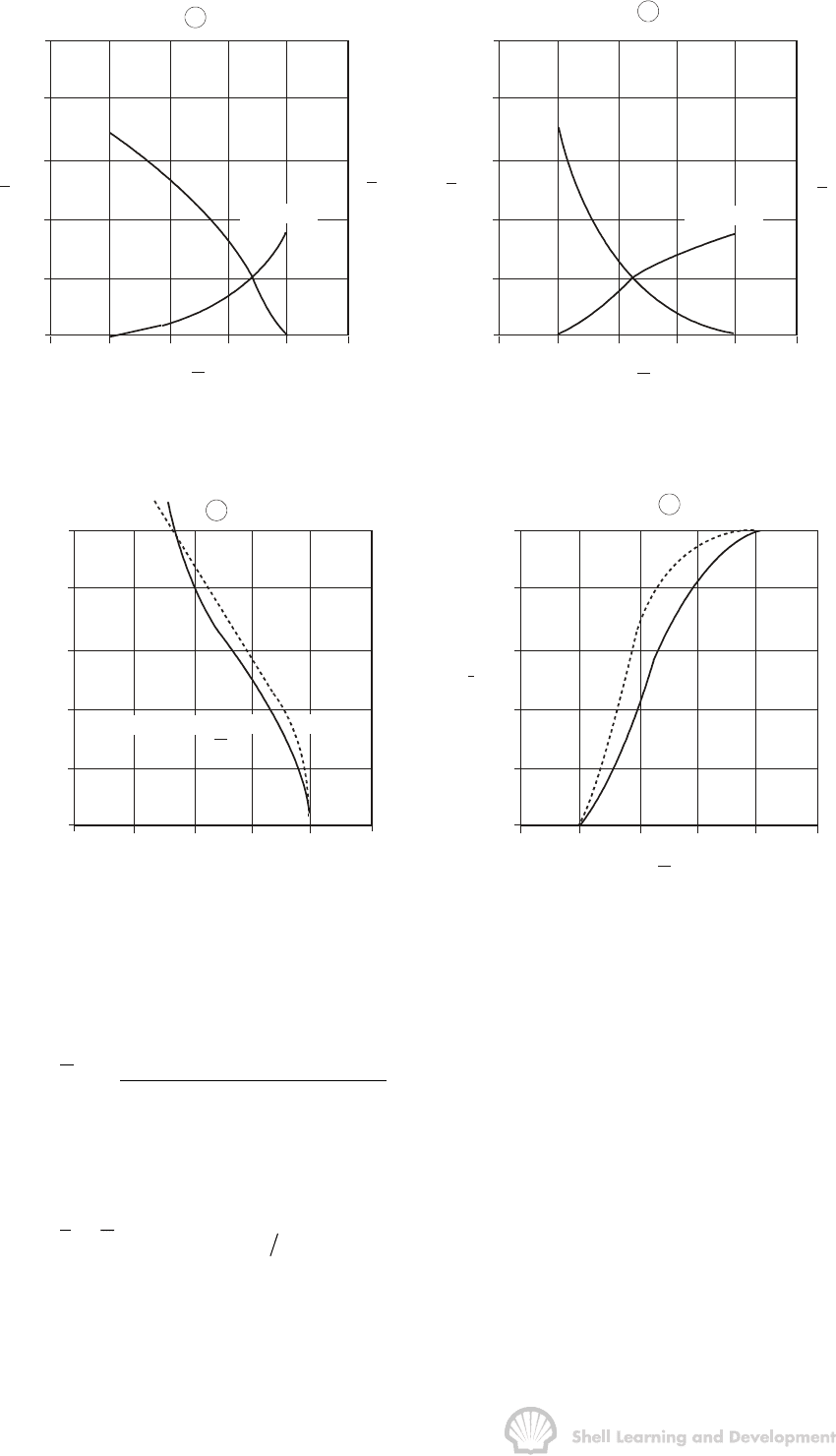
IMMISCIBLE DISPLACEMENT 396

1.0

.2 .4

.6 .8 1.0

OIL

WATER

1.0

.2 .4

.6 .8 1.0

OIL

WATER

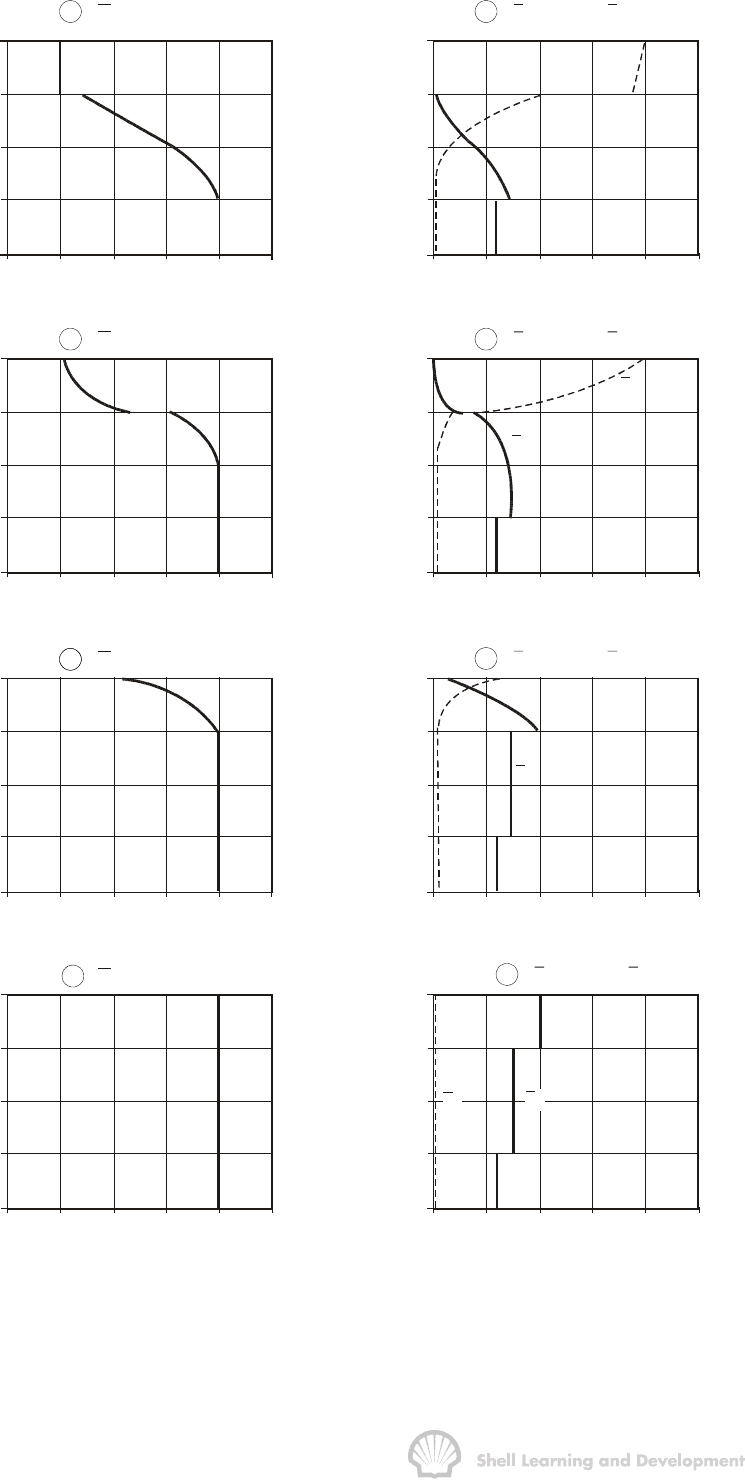
Fig. 10.38 Averaged relative permeability functions for the three layered reservoir,

fig. 10.34: (a) high permeability layer at top, (b) at base of the reservoir

.2 .4

.6 .8 1.

-1

-2

.2 .4

.6 .8

1.0

Fig. 10.39 (a) Pseudo capillary pressure, and (b) fractional flow curves for the three

layered reservoir, fig. 10.34). (——high permeability at top;

−

−−

− −

−−

− −

−−

−at base of the

reservoir).

jor jjwc

j1 jn1

h(1S) hS

φφ

==+

−+

åå

(10.72)

while the corresponding averaged relative permeabilities to water and oil are

jrw j j

j1 j1

k(S) hkk hk

′

åå

(10.73)

and

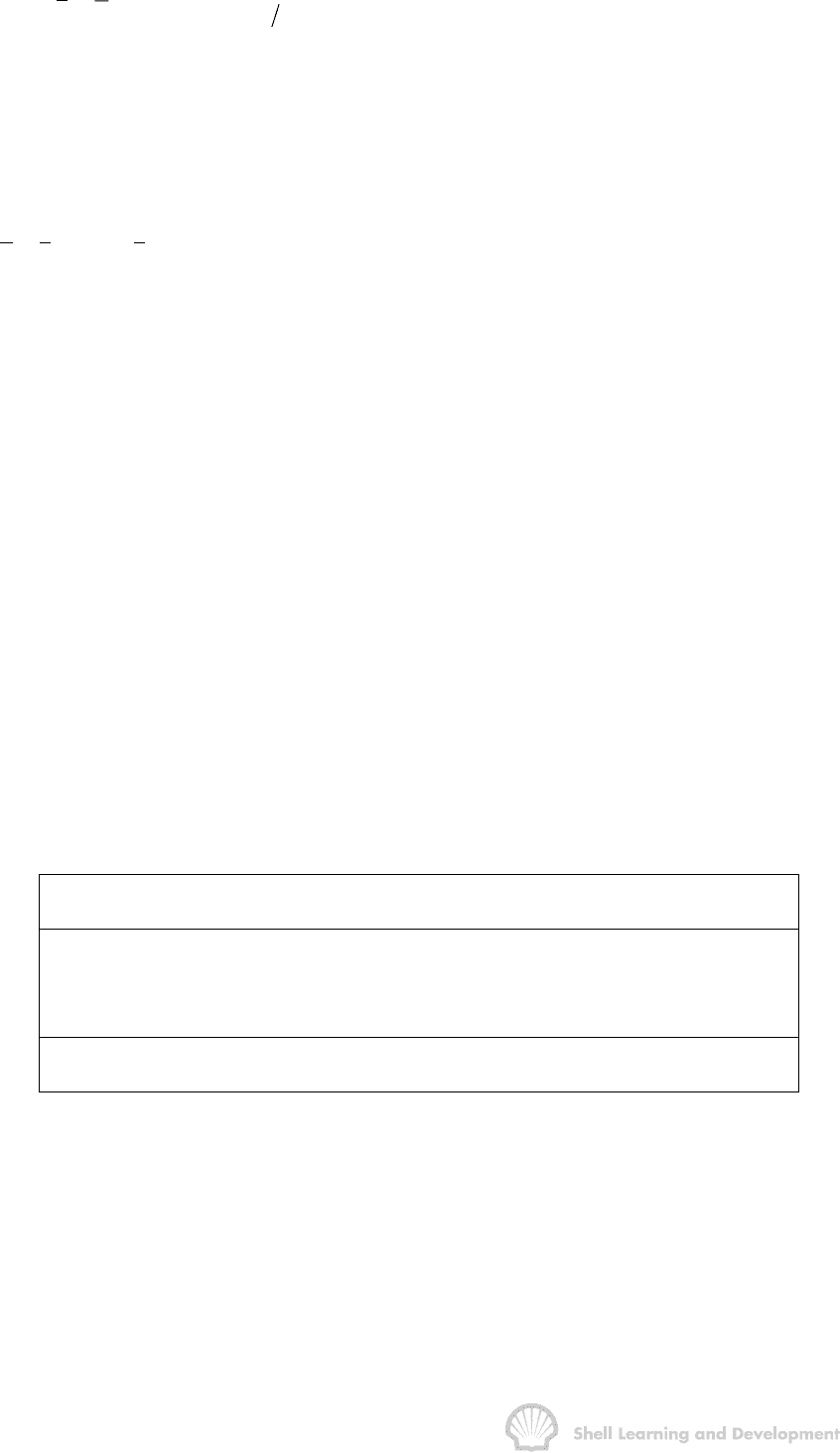
IMMISCIBLE DISPLACEMENT 397

jro jj

jn1 j1

k(S) hkk hk

=+ =

′

åå

(10.74)

where

′

and

′

are the end point relative permeabilities to water and oil in the j

layer, for water saturations

(1 S )−

and

, respectively. Furthermore, as

demonstrated in sec. 10.6, as the water-oil interface rises in any given layer the water

saturation and relative permeabilities for the layer increase in direct proportion to the

fractional thickness of the water. Thus the discrete values of

rw ro

S,k andk calculated using equs. (10.72-74) are connected to the values

calculated for n - 1 and n + 1 by straight lines. The averaged relative permeability

curves are therefore made up of straight line segments as illustrated in the following

exercise.

EXERCISE 10.4 GENERATION OF AVERAGED RELATIVE PERMEABILITY

CURVES FOR A LAYERED RESERVOIR (SEGREGATED FLOW)

Generate and plot the averaged relative permeabilities and the pseudo capillary

pressure relationship, as functions of the thickness averaged water saturation, for the

40 ft. thick reservoir described in this section, fig.10.34, assuming that flow will take

place under segregated conditions (no capillary transition zone). The end point relative

permeabilities and saturations for each layer may be taken from fig. 10.35 (a)-(c) and

the specific gravities of the water and oil are 1.04 and 0.81, respectively.

Repeat the exercise with the reservoir model inverted so that the high permeability

layer is at the base of the reservoir.

EXERCISE 10.4 SOLUTION

Figure 10.40 includes all the data for the three-layered reservoir specified in the

question.

layer 3 h

= 10ft.; k

= 200mD; φ

= .20;

k.4;

′

k.8;

′

layer 2 h

= 20ft.; k

= 100mD; φ

= .17;

k.6;

′

k.6;

′

layer 1 h

= 10ft.; k

= 50mD; φ

= .15;

k.25;

′

k.5;

′

Fig. 10.40 Individual layer properties; exercise 10.4

In addition, the end point saturations in each layer are S

= S

= 0.2 and

h 6.9 ft

h k 4500 mD.ft

IMMISCIBLE DISPLACEMENT 398

When there is only connate water in each layer the initial average saturation and

relative permeabilities can be determined as (n=0)

jj wc jj

j1 j1

ShS h0.2

φφ

åå

k(S) 0=

and

jjro jj

j1 j1

k(S) hkk hk 0.678

′

åå

As the water-oil interface rises in the reservoir, values of

S,k (S)and

k(S)can be computed using equs. (10.72-74), as n varies from 1 to 3, giving the

values listed in table 10.13.

0 .200 0 .678 2.0

1 .330 .028 .622 1.0

2 .626 .161 .356 -1.0

3 .800 .339 0 -2.0

TABLE 10.13

For instance, when n=2, so that the water-oil interface has risen to the top of the middle

layer,

123

11 or 22 or 33 wc j1

S(h(1S)h(1S)hS)/h

φφ φ φ

=−+−+

= (10× .15×.8 + 20×.17×.8 + 10× .20×.2) /6.9 = 0.626

1 1 rw 2 2 rw j j

k(S) (hkk hkk)/ hk

′′

= (10×50×.25 + 20×100×.3) /4500 = 0.161

and

33ro jj

k(S) hkk / hk

′

= 10×200×.8 / 4500 = 0.356

The pseudo capillary pressures have again been calculated using the equation

c1S

P0.1(20z)

−

=− (10.70)

where

−

is the elevation of the water-oil interface above the base of the reservoir.

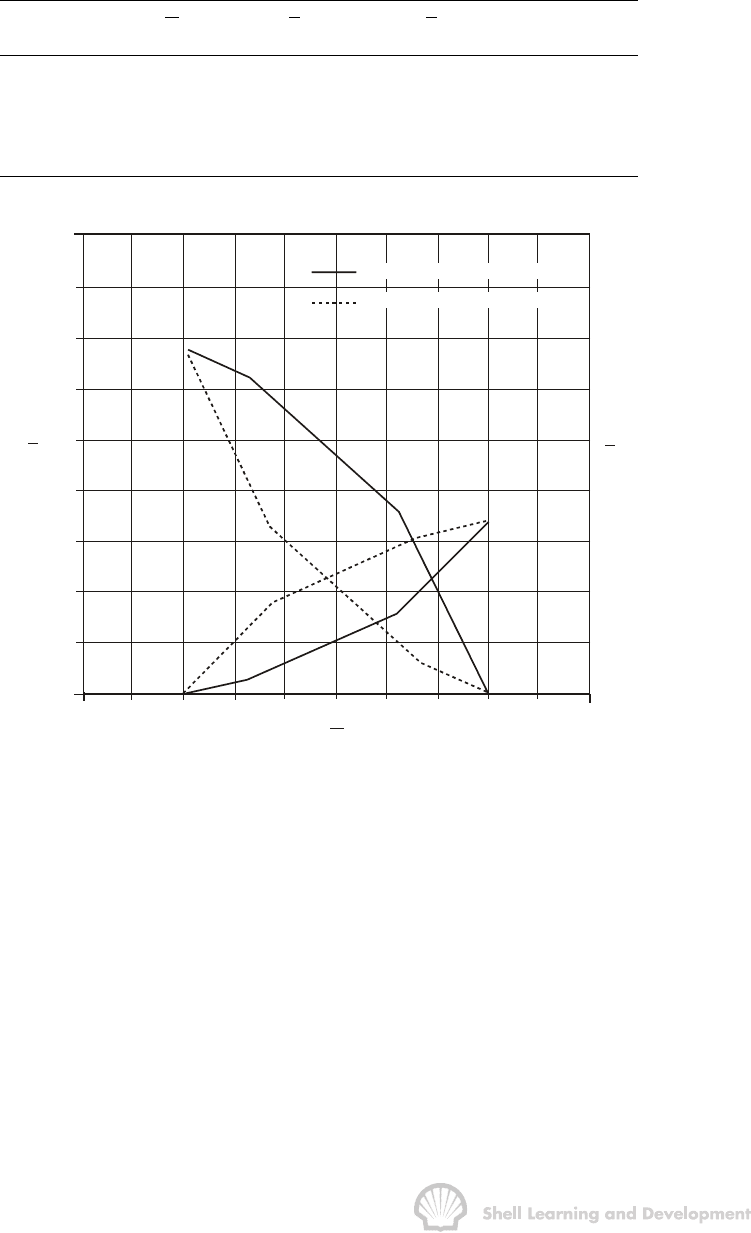
IMMISCIBLE DISPLACEMENT 399

If the reservoir were inverted, the reader can verify that the average saturations,

relative permeabilities and pseudo capillary pressures would be as listed in table 10.14,

in which the layer ordering has now been reversed.

The averaged relative permeabilities and pseudo capillary pressure functions are

plotted in figs. 10.41 and 42(a), respectively, each consisting of a series of linear

segments.

0 .200 0 .678 2.0

1 .374 .178 .322 1.0

2 .670 .311 .056 -1.0

3 .800 .339 0 -2.0

TABLE 10.14

.1 .2

.5 .6

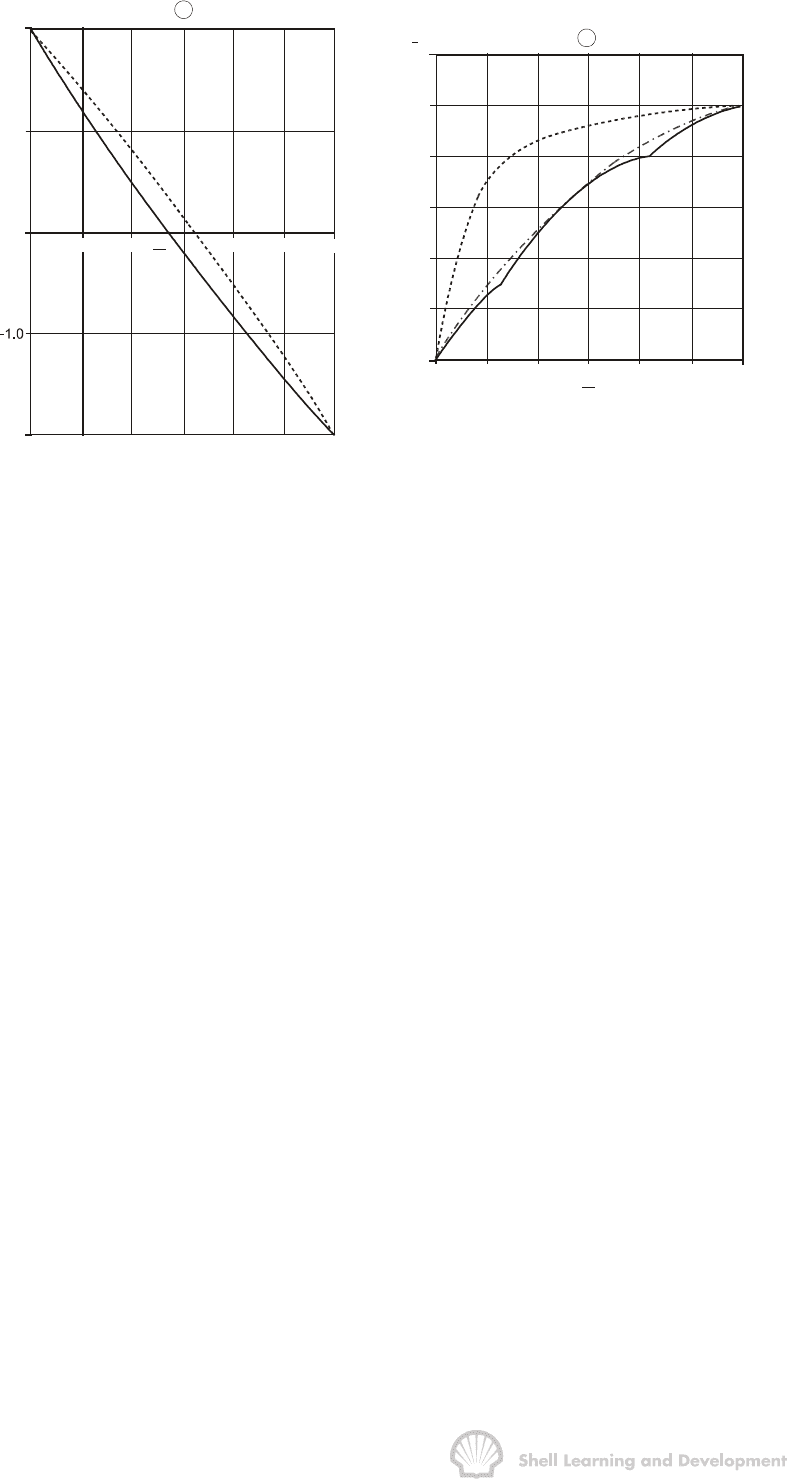
.8 .9 1.0

HIGH PERMEABILITY - TOP

HIGH PERMEABILITY - BASE

Fig. 10.41 Averaged relative permeability curves; exercise 10.4

IMMISCIBLE DISPLACEMENT 400

1.0

.2 .3 .4 .5 .6 .7 .8

.3 .4 .6

2.0

1.0

-2.0

(psi)

Fig. 10.42 (a) Pseudo capillary pressures, and (b) fractional flow curves, exercise 10.4

(—— High permeability layer at top;

−

−−

− −

−−

− −

−−

−at base of reservoir)

Inversion of the reservoir, so that the highest permeability layer is at the base, results

in the functions represented by the dashed lines, which are simply reflections of the

originals. Also shown in fig. 10.42(b) are the fractional flow curves for the two cases

which again indicate that the displacement is much more favourable if the high

permeability layer is at the top of the reservoir, since vertical fluid movement is

dependent on gravity alone. While the fractional flow curve for the favourable case

(solid line), increases continuously with increasing water saturation, the derivative of

the curve, which is required in oil recovery calculations, does not. Therefore to use the

curve, in conjunction with the Welge graphical technique for determining oil recovery,

requires that it first be smoothed, as shown in fig. 10.42(b). This smoothing is

unnecessary in the case of unfavourable displacement, with the high permeability layer

at the base of the reservoir (dashed line).

b) No pressure communication between the layers

If the individual layers are isolated from one another by impermeable barriers so that

there is a lack of pressure communication between them, there will be no flow of fluids

in the dip normal direction. Even though injection and production wells are completed

across all the layers the problem is one of dealing with a set of isolated reservoirs

between which pressure communication can only exist in the wellbore.

Stiles has presented a simple, approximate method

for calculating oil recovery under

these circumstances and further examples of its application have been presented by

Craft and Hawkins

and Cole

. Fundamental to the Stiles method is the assumption

that piston-like displacement occurs in each separate layer, which is equivalent to

assuming that the end point mobility ratio is unity. Furthermore, for this stable

displacement the oil and water must have the same velocity which, applying Darcy's

law, implies that